湘教版2023-2024学年度上学期七年级期末模拟数学试题2(含解析)
文档属性
| 名称 | 湘教版2023-2024学年度上学期七年级期末模拟数学试题2(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-02 20:52:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
湘教版2023-2024七年级上期末模拟试题2
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
2的相反数是( )
A.﹣2 B.2 C.﹣ D.
下列等式的变形正确的是( )
A.如果s=vt,那么v= B.如果x=6,那么x=3
C.如果﹣x﹣1=y﹣1,那么x=y D.如果a=b,那么a+2=2+b
如图的图形,是由( )旋转形成的.
A. B. C. D.
国家统计局数据显示,截至2014年末全国商品房待售面积约为62200万平方米,该数据用科学记数法可表示为( )
A.6.22×104 B. 6.22×107 C. 6.22×108 D. 6.22×109
为了解某校七年级500名学生身高情况,从中抽取了50名学生进行检测,这50名学生的身高是( )
A.总体 B.个体 C.样本容量 D.总体的一个样本
计算:(﹣3)+4的结果是( )
A.﹣7 B.﹣1 C.1 D.7
某土建工程共需动用30台挖运机械,每台机械每分钟能挖土3m3,或者运土2m3,为了使挖土和运土工作同时结束,安排了x台机械挖土,这里的x应满足的方程是( )
A. B. C. D.
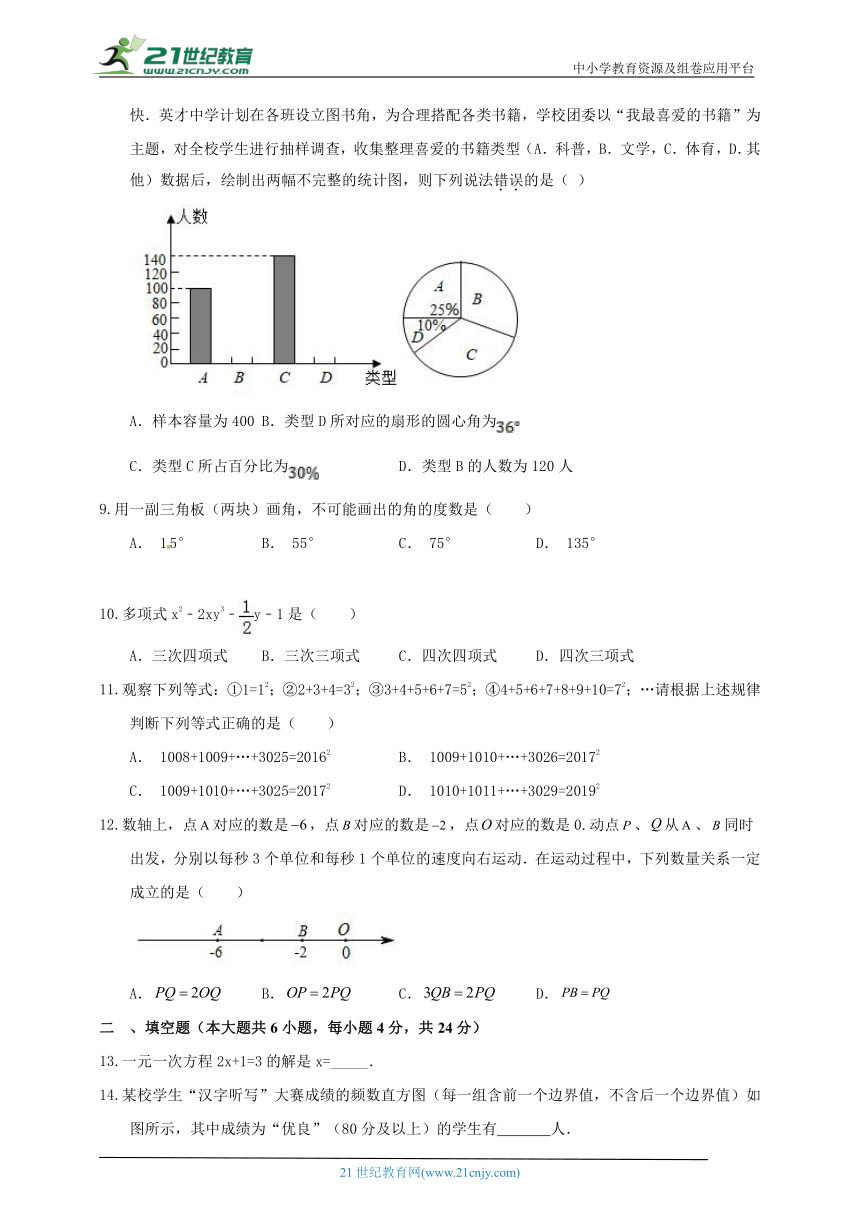
高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
A.样本容量为400 B.类型D所对应的扇形的圆心角为
C.类型C所占百分比为 D.类型B的人数为120人
用一副三角板(两块)画角,不可能画出的角的度数是( )
A. 15° B. 55° C. 75° D. 135°
多项式x2﹣2xy3﹣y﹣1是( )
A.三次四项式 B.三次三项式 C.四次四项式 D.四次三项式
观察下列等式:①1=12;②2+3+4=32;③3+4+5+6+7=52;④4+5+6+7+8+9+10=72;…请根据上述规律判断下列等式正确的是( )
A. 1008+1009+…+3025=20162 B. 1009+1010+…+3026=20172
C. 1009+1010+…+3025=20172 D. 1010+1011+…+3029=20192
数轴上,点对应的数是,点对应的数是,点对应的数是0.动点、从、同时出发,分别以每秒3个单位和每秒1个单位的速度向右运动.在运动过程中,下列数量关系一定成立的是( )
A. B. C. D.
1 、填空题(本大题共6小题,每小题4分,共24分)
一元一次方程2x+1=3的解是x=_____.
某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“优良”(80分及以上)的学生有 人.
已知,且,则的值是___.
将(2a+3)看作一个整体,化简(2a+3)2+6(2a+3)2=___________.
要制作一批盒装月饼,每盒装2块大月饼和6块小月饼,制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉,则生产_____盒月饼正好共用面粉440kg.
一个电子跳蚤在数轴上做跳跃运动.第一次从原点O起跳,落点为A1,点A1表示的数为1;第二次从点A1起跳,落点为OA1的中点A2;第三次从A2点起跳,落点为0A2的中点A3;如此跳跃下去……最后落点为OA2019的中点A2020.则点A2020表示的数为__________.
1 、解答题(本大题共8小题,共78分)
计算:﹣12014﹣6÷(﹣2)×|﹣|.
解下列方程
(1);
(2)
(3)
(4)
先化简,再求值:(﹣x2+5x+4)+(5x﹣4+2x2),其中x=﹣2.
小黄做一道题“已知两个多项式A,B,计算A﹣B”.小黄误将A﹣B看作A+B,求得结果是9x2﹣2x+7.若B=x2+3x﹣2,请你帮助小黄求出A﹣B的正确答案.
中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如图所示:
本数(本) 频数(人数) 频率
5 a 0.2
6 18 0.36
7 14 b
8 8 0.16
合计 c 1
(1)统计表中的a= ,b= ,c= ;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的人数.
学校组织游学活动,去往北京市某公园,公园门票价格规定如下表:
购票张数 1﹣50张 51﹣100张 100张以上
单张票价 13元 11元 9元
北京线路共有104人参加本次游园,分两车出发,编号为1号和2号.其中1号车有40多人,不足50人.经估算,如果两辆车以车为单位购票,则一共应付1240元.
(1)1号车与2号车各有多少学生?
(2)若两车联合起来,作为一个团体购票,可省多少钱?
(3)若1号车单独组织去游园,如何购票才最省钱,并说明理由.
如图,点 A在数轴上表示的数是-6,点 B在数轴上表示的数是12
(1)线段AB的长为_______;线段AB的中点表示的数是______
(2)点C是数轴上的一个动点,当 AC-3BC=6 时,点 C表示的数是多少?
已知点O在直线MN上,过点O作射线OP,使∠MOP=130°,现将一块直角三角板的直角顶点始终放在点O处.
(1)如图①,当三角板的一边OA在射线OM上,另一边OB在直线MN的上方时,∠POB的度数 是 ;
(2)若将三角板绕点O旋转至图②所示的位置,此时OB恰好平分∠PON,则∠BOP 的度数为 ;∠AOM 的度数为 ;
(3)若将三角板绕点O旋转至图③所示位置,此时OA在∠PON 的内部,
①若 OP 所在的直线平分∠MOB,则∠POA 的度数为 ;
②∠BON-∠POA的度数为 .
答案解析
1 、选择题
【考点】相反数.
【分析】只有符号不同的两个数叫做互为相反数,由此即可得到答案.
解:2的相反数是﹣2.
故选:A.
【点评】本题考查相反数,关键是掌握相反数的定义.
【考点】等式的性质.
【分析】的两边同时乘以或除以同一个不为0数或字母,等式仍成立,可得答案.
解:A.左边乘以,右边乘以,故A错误;
B、左边乘以2,右边乘以,故B错误;
C、左边加(2x+1),右边加1,故C错误;
D、两边都加2,故D正确;
故选:D.
【点评】本题主要考查了等式的基本性质,等式的两边同时加上或减去同一个数或字母,等式仍成立;等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.
【考点】点、线、面、体
【分析】根据每一个几何体的特征判断即可.
解:A.可以旋转形成圆台;
B.可以旋转形成球;
C.可以旋转形成圆柱;
D.可以旋转形成圆锥;
故选:A.
【点评】本题考查了点、线、面、体,熟练掌握每一个几何体的特征是解题的关键.
【考点】科学记数法—表示较大的数..
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解:将62200万用科学记数法表示为6.22×108.
故选C
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
【考点】总体、个体、样本、样本容量.
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
解:为了解某校七年级500名学生身高情况,从中抽取了50名学生进行检测,这50名学生的身高是总体的一个样本,
故选:D.
【点评】本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
【考点】有理数的加法.
【分析】根据异号两数相加,取绝对值较大的数的符号,再用较大的绝对值减去较小的绝对值,可得答案.
解:原式=+(4﹣3)=1.
故选:C.
【点评】此题主要考查了有理数加法,正确掌握运算法则是解题关键。
【考点】一元一次方程的应用-配套问题
【分析】根据安排x台机械挖土,则有(30-x)台机械运土,x台机械挖土的总数为3xm3,则(30-x)台机械运土总数为2(30-x)m3,进而得出方程.
解:设安排x台机械挖土,则有(30-x)台机械运土,x台机械挖土的总数为3xm3,则(30-x)台机械运土总数为2(30-x)m3,
根据挖出的土等于运走的土,得:3x=2(30-x).
故选:D.
【点评】此题主要考查了由实际问题抽象出一元一次方程,找出题目蕴含的数量关系是解决问题的关键.
【考点】条形统计图,扇形统计图
【分析】根据类型的条形统计图和扇形统计图信息可判断选项;利用乘以可判断选项;利用类型的人数除以样本总人数可判断选项;利用类型所在百分比乘以样本总人数即可判断选项.
解:,则样本容量为400,选项A说法正确;
,则选项B说法正确;
,则选项C说法错误;
(人),则选项D说法正确;
故选:C.
【点评】本题考查了条形统计图和扇形统计图的信息关联,熟练掌握统计调查的相关知识是解题关键.
【考点】角的计算.
【分析】解答此题的关键是分清两块三角板的锐角度数的度数分别是多少,然后对应着4个选项再进行组合,看看可能画出的角的度数是多少即可.
解:两块三角板的锐角度数分别为:30°,60°;45°,45°
用一块三角板的45°角和另一块三角板的30°角组合可画出15°、75°角,
用一块三角板的直角和和另一块三角板的45°角组合可画出135°角,
无论两块三角板怎么组合也不能画出55°角.
故选B.
【点评】此题主要考查学生对角的计算这一知识点的理解和掌握,解答此题的关键是分清两块三角板的锐角度数的度数分别是多少,比较简单,属于基础题.
【考点】多项式
【分析】先观察多项式的项数,再确定每项的次数,最高次项的次数就是多项式的次数.
解:多项式x2﹣2xy3﹣y﹣1有四项,最高次项﹣2xy3的次数为四,是四次四项式.
故选:C.
【点评】本题考查了多项式的项和次数定义.多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.
【考点】探索规律
【分析】根据题目中各个式子的变化规律为n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2,可以判断各个选项中的等式是否成立,从而可以解答本题.
解:由题意可得:1008+1009+…+3022+(3023+3024+3025)=()2+9072=20152+9072≠20162.故选项A错误.
1009+1010+…+3025+3026=()2+3026=20172+3026.故选项B错误.
1009+1010+…+3025=()2=20172.故选项C正确.
1010+1011+…+3029=()2+3029=20192+3029.故选项D错误.
故选C.
【点评】本题考查了有理数的混合运算、规律型:数字的变化类,解答本题的关键是明确题意,发现各个式子的变化规律,可以判断各个选项中的等式是否成立.
【考点】线段的和差,数轴
【分析】设运动时间为t秒,根据题意可知AP=3t,BQ=t,AB=2,然后分类讨论:①当动点P、Q在点O左侧运动时,②当动点P、Q运动到点O右侧时,利用各线段之间的和、差关系即可解答.
解:设运动时间为t秒,由题意可知: AP=3t, BQ=t,
AB=|-6-(-2)|=4,BO=|-2-0|=2,
①当动点P、Q在点O左侧运动时,
PQ=AB-AP+BQ=4-3t+t=2(2-t),
∵OQ= BO- BQ=2-t,
∴PQ= 2OQ ;
②当动点P、Q运动到点O右侧时,
PQ=AP-AB-BQ=3t-4-t=2(t-2),
∵OQ=BQ- BO=t-2,
∴PQ= 2OQ,
综上所述,在运动过程中,线段PQ的长度始终是线段OQ的长的2倍,
即PQ= 2OQ一定成立.
故选:A.
【点评】本题考查了数轴上的动点问题及数轴上两点间的距离,解题时注意分类讨论的运用.
1 、填空题
【考点】解一元一次方程
【分析】将方程移项,然后再将系数化为1即可求得一元一次方程的解.
解:将方程移项得,
2x=2,
系数化为1得,
x=1.
故答案为:1.
【点评】此题主要考查学生对解一元一次方程这一知识点的理解和掌握,此题比较简单,属于基础题
【考点】频数(率)分布直方图
【分析】根据题意和直方图中的数据可以求得成绩为“优良”(80分及以上)的学生人数,本题得以解决.
解:由直方图可得,
成绩为“优良”(80分及以上)的学生有:60+30=90(人),
故答案为:90.
【点评】本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
【考点】绝对值。有理数的混合运算
【分析】根据绝对值的性质求出x的值,再根据有理数的加法运算法则判断出x、y的对应情况,然后代入计算即可得解.
解:∵,
∴,
∵,,
∴,
∴.
故答案为:-4.
【点评】本题考查有理数的加法、绝对值、有理数的混合运算,解题的关键是能根据题目中的信息确定x、y的值.
【考点】同类项,合并同类项
【分析】运用整体思想,将(2a+3)看作一个整体,(2a+3)2+6(2a+3)2=7(2a+3)2.
解:将(2a+3)看作一个整体,化简(2a+3)2+6(2a+3)2=7(2a+3)2
故答案为:7(2a+3)2
【点评】本题考核知识点:合并同类项. 解题关键点:运用整体思想进行化简.
【考点】一元一次方程的应用-配套问题
【分析】设用xkg面粉制作大月饼,则利用(440﹣x)kg制作小月饼,根据题意得到2×小月饼的块数=6×大月饼的块数,依此列出方程.
解:设用xkg面粉制作大月饼,则利用(440﹣x)kg制作小月饼,根据题意得出:
,
解得:x=200,
则440﹣200=220(kg).
所以÷2=8000(盒)
故答案是:8000.
【点评】此题考察一元一次方程的实际应用,正确理解题意是解题的关键,此题找到大小月饼的数量关系即2×小月饼的块数=6×大月饼的块数,设出未知数依据题意列出方程即可得到答案.
【考点】数轴,线段中点
【分析】先根据数轴的定义、线段中点的定义分别求出点表示的数,再归纳类推出一般规律,由此即可得.
解:由题意得:点表示的数为
点表示的数为
点表示的数为
点表示的数为
归纳类推得:点表示的数为(n为正整数)
则点表示的数为
故答案为:.
【点评】本题考查了数轴的定义、线段中点的定义,根据点表示的数,正确归纳类推出一般规律是解题关键.
1 、解答题
【考点】有理数的混合运算.
【分析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解:原式=﹣1+6××=﹣1+1=0.
【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
【考点】解一元一次方程
【分析】(1)移项合并后化系数为1即可.
(2)先去括号,然后再进行移项合并.
(3)按解一元一次方程的一般步骤进行解答即可.
(4)此题比较麻烦,要根据步骤一步一步的进行.
解:(1)解:移项合并同类项得,10x=10,
系数化为得,x=1;
(2)解:去括号得,6-2x=-4x-20,
移项合并同类项得,2x=-26,
系数化为1得,x=-13;
(3)解:去分母得,3(x-7)-4(5x+8)=12,
去括号得,3x-21-20x-32=12,
移项合并同类项得,-17x=65,
系数化为1得,x= ;
(4)解:去括号得,2x-x+x-=x-,
去分母得,24x-6x+3x-3=8x-8,
移项合并同类项得,13x=-5,
系数化为1得,x=-.
【点评】本题考查解一元一次方程的知识,题目难度不大,但是出错率很高,是失分率很高的一类题目,同学们要在按步骤解答的基础上更加细心的解答.
【考点】整式的加减—化简求值
【分析】本题考查了整式的加减、去括号法则两个考点.先按照去括号法则去掉整式中的小括号,再合并整式中的同类项即可.
解:原式=(﹣x2+5x+4)+(5x﹣4+2x2)
=﹣x2+5x+4+5x﹣4+2x2=x2+10x
=x(x+10).
∵x=﹣2,
∴原式=﹣16.
【点评】解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.然后代入求值即可.
【考点】整式的加减.
【分析】根据题意可得出A的值,再计算A﹣B即可.
解:∵A+B=9x2﹣2x+7,B=x2+3x﹣2,
∴A=9x2﹣2x+7﹣(x2+3x﹣2)
=9x2﹣2x+7﹣x2﹣3x+2
=8x2﹣5x+9,
∴A﹣B=8x2﹣5x+9﹣(x2+3x﹣2)
=8x2﹣5x+9﹣x2﹣3x+2
=7x2﹣8x+11.
【考点】用样本估计总体;频数(率)分布表;频数(率)分布直方图
【分析】(1)根据百分比=计算即可;
(2)求出a组人数,画出直方图即可;
(3)根据平均数的定义计算即可;
(4)利用样本估计总体的思想解决问题即可;
解:(1)由题意c=18÷0.36=50,
∴a=50×0.2=10,b==0.28,
故答案为10,0.28,50.
(2)频数分布表直方图如图所示.
(3)所有被调查学生课外阅读的平均本数==6.4(本)
(4)该校八年级共有1200名学生,该校八年级学生课外阅读7本及以上的人数有1200×=528(名).
【点评】本题考查频数分布直方图、扇形统计图、样本估计总体等知识,解题的关键是熟练掌握基本概念,灵活运用所学知识解决问题,属于中考常考题型.
【考点】一元一次方程的应用-方案选择
【分析】(1)设1号车有x个学生,则2号车有(104-x)个学生,根据购票总费用=1号车购票费用+2号车购票费用即可得出关于x的一元一次方程,解之即可得出结论;
(2)求出购买104张票的总钱数,将其与1240做差即可得出结论;
(3)分别求出购买48张门票以及购买51张门票的总钱数,比较后即可得出结论.
解:(1)设1号车有x个学生,则2号车有(104﹣x)个学生,
根据题意得:13x+11(104﹣x)=1240,
解得:x=48,
∴104﹣x=56.
答:1号车有48个学生,2号车有56个学生.
(2)1240﹣9×104=304(元).
答:如果两车联合起来,作为一个团体购票,可省304元钱.
(3)51×11=561(元),48×13=624(元),
∴561<624,
∴如果1号车单独组织去游园,购买51张门票最省钱.
【点评】本题考查了一元一次方程的应用,解题的关键是:(1)根据购票总费用=1号车购票费用+2号车购票费用列出关于x的一元一次方程;(2)根据总价=单价×数量求出购买104张门票的总钱数;(3)根据总价=单价×数量分别求出购买48张门票以及购买51张门票的总钱数.
【考点】线段的和差,线段的中点,数轴,一元一次方程的应用
【分析】(1)由数轴两点距离求法AB=12-(-6)=18;设线段AB的中点为E,由线段中点得AE=BE=,由距离求法OE=OB-EB=3;
(2)根据点C的位置进行分类考虑①当点 C 在 AB 之间时, ②当点 C 在点 B 右侧时,设设点C表示的数为x,③当点C在点A左侧时,根据 AC-3BC=6 列方程解之即可.
(1)点 A在数轴上表示的数是-6,点 B在数轴上表示的数是12,
AB=12-(-6)=12+6=18,
设线段AB的中点为E,
则AE=BE=,
OE=OB-EB=12-9=3,
线段AB的中点表示的数是3,
故答案为:18;3 ;
(2)①当点 C 在 AB 之间时,设点C表示的数为x,则 AC=x+6,BC=12-x,
∵AC-3BC=6,
x+6-3(12-x)=6 ,
解答 x=9,
点 C 表示的数为 9 ,
②当点 C 在点 B 右侧时,设设点C表示的数为x,则 AC=x+6,BC= x -12,
∵AC-3BC=6 ,
x+6-3(x-12)=6 ,
解答 x=18,
点 C 表示的数为 18,
③当点C在点A左侧时,AC当 AC-3BC=6 时,点 C表示的数是9或18.
【点评】本题考查数轴两点间距离,线段中点,利用线段和差列简单方程,会解方程,会根据点的位置分类讨论是解题关键.
【考点】余角和补角,角的计算
【分析】(1)根据∠POB=∠MOP-∠AOB代入数据即可求出结论;
(2)根据∠PON=180°-∠MOP可算出∠PON的度数,根据OB平分∠PON即可求出∠POB的度数,再通过角的计算可得出∠AOP=60°,结合∠MOP=130°即可得出∠AOM;
(3)①根据OP 所在的直线平分∠MOB,可得出∠MOB=100°,从而可求出∠BON=80°,根据∠BOA=90°求出∠AON=10°,根据∠POA=∠PON-∠AON可得结论;
②设∠AON=x°,则∠BON=90°-x°,∠POA=50°-x°,二者做差即可得出结论.
解:(1)∠POB=∠MOP-∠AOB=130°-90°=40°.
(2)∵∠MON是平角,∠MOP=130゜,
∴∠PON=∠MON-∠MOP=180゜-130゜=50゜
∵OB 平分∠PON,
∴∠BOP=∠PON=25゜
∵∠AOB=90゜,
∴∠AOP=∠AOB-∠BOP=90゜-25゜=65゜
∴∠MOA=∠MOP-∠AOP=130゜-65゜=65゜;
(3)①如图,OE是PO的延长线,
∵∠MOP=130゜
∴∠MOE=50゜
∵OE是∠MOB的平分线,
∴∠MOB=100゜,
∴∠BON=80゜
∵∠AOB=90゜
∴∠AON=∠AOB-∠BON=90゜-80゜=10゜
∴∠POA=∠PON-∠AON=50゜-10゜=40゜;
②设∠AON=x°,则∠BON=90°-x°,∠POA=50°-x°,
∴∠BON-∠POA=(90°-x°)-(50°-x°)=40°.
【点评】本题考查了余角和补角以及角的计算,通过角的计算找出各角之间的关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
湘教版2023-2024七年级上期末模拟试题2
姓名:__________班级:__________考号:__________总分__________
1 、选择题(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
2的相反数是( )
A.﹣2 B.2 C.﹣ D.
下列等式的变形正确的是( )
A.如果s=vt,那么v= B.如果x=6,那么x=3
C.如果﹣x﹣1=y﹣1,那么x=y D.如果a=b,那么a+2=2+b
如图的图形,是由( )旋转形成的.
A. B. C. D.
国家统计局数据显示,截至2014年末全国商品房待售面积约为62200万平方米,该数据用科学记数法可表示为( )
A.6.22×104 B. 6.22×107 C. 6.22×108 D. 6.22×109
为了解某校七年级500名学生身高情况,从中抽取了50名学生进行检测,这50名学生的身高是( )
A.总体 B.个体 C.样本容量 D.总体的一个样本
计算:(﹣3)+4的结果是( )
A.﹣7 B.﹣1 C.1 D.7
某土建工程共需动用30台挖运机械,每台机械每分钟能挖土3m3,或者运土2m3,为了使挖土和运土工作同时结束,安排了x台机械挖土,这里的x应满足的方程是( )
A. B. C. D.
高尔基说:“书,是人类进步的阶梯”.阅读可以丰富知识,拓展视野,充实生活,给我们带来愉快.英才中学计划在各班设立图书角,为合理搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅不完整的统计图,则下列说法错误的是( )
A.样本容量为400 B.类型D所对应的扇形的圆心角为
C.类型C所占百分比为 D.类型B的人数为120人
用一副三角板(两块)画角,不可能画出的角的度数是( )
A. 15° B. 55° C. 75° D. 135°
多项式x2﹣2xy3﹣y﹣1是( )
A.三次四项式 B.三次三项式 C.四次四项式 D.四次三项式
观察下列等式:①1=12;②2+3+4=32;③3+4+5+6+7=52;④4+5+6+7+8+9+10=72;…请根据上述规律判断下列等式正确的是( )
A. 1008+1009+…+3025=20162 B. 1009+1010+…+3026=20172
C. 1009+1010+…+3025=20172 D. 1010+1011+…+3029=20192
数轴上,点对应的数是,点对应的数是,点对应的数是0.动点、从、同时出发,分别以每秒3个单位和每秒1个单位的速度向右运动.在运动过程中,下列数量关系一定成立的是( )
A. B. C. D.
1 、填空题(本大题共6小题,每小题4分,共24分)
一元一次方程2x+1=3的解是x=_____.
某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“优良”(80分及以上)的学生有 人.
已知,且,则的值是___.
将(2a+3)看作一个整体,化简(2a+3)2+6(2a+3)2=___________.
要制作一批盒装月饼,每盒装2块大月饼和6块小月饼,制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉,则生产_____盒月饼正好共用面粉440kg.
一个电子跳蚤在数轴上做跳跃运动.第一次从原点O起跳,落点为A1,点A1表示的数为1;第二次从点A1起跳,落点为OA1的中点A2;第三次从A2点起跳,落点为0A2的中点A3;如此跳跃下去……最后落点为OA2019的中点A2020.则点A2020表示的数为__________.
1 、解答题(本大题共8小题,共78分)
计算:﹣12014﹣6÷(﹣2)×|﹣|.
解下列方程
(1);
(2)
(3)
(4)
先化简,再求值:(﹣x2+5x+4)+(5x﹣4+2x2),其中x=﹣2.
小黄做一道题“已知两个多项式A,B,计算A﹣B”.小黄误将A﹣B看作A+B,求得结果是9x2﹣2x+7.若B=x2+3x﹣2,请你帮助小黄求出A﹣B的正确答案.
中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如图所示:
本数(本) 频数(人数) 频率
5 a 0.2
6 18 0.36
7 14 b
8 8 0.16
合计 c 1
(1)统计表中的a= ,b= ,c= ;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的人数.
学校组织游学活动,去往北京市某公园,公园门票价格规定如下表:
购票张数 1﹣50张 51﹣100张 100张以上
单张票价 13元 11元 9元
北京线路共有104人参加本次游园,分两车出发,编号为1号和2号.其中1号车有40多人,不足50人.经估算,如果两辆车以车为单位购票,则一共应付1240元.
(1)1号车与2号车各有多少学生?
(2)若两车联合起来,作为一个团体购票,可省多少钱?
(3)若1号车单独组织去游园,如何购票才最省钱,并说明理由.
如图,点 A在数轴上表示的数是-6,点 B在数轴上表示的数是12
(1)线段AB的长为_______;线段AB的中点表示的数是______
(2)点C是数轴上的一个动点,当 AC-3BC=6 时,点 C表示的数是多少?
已知点O在直线MN上,过点O作射线OP,使∠MOP=130°,现将一块直角三角板的直角顶点始终放在点O处.
(1)如图①,当三角板的一边OA在射线OM上,另一边OB在直线MN的上方时,∠POB的度数 是 ;
(2)若将三角板绕点O旋转至图②所示的位置,此时OB恰好平分∠PON,则∠BOP 的度数为 ;∠AOM 的度数为 ;
(3)若将三角板绕点O旋转至图③所示位置,此时OA在∠PON 的内部,
①若 OP 所在的直线平分∠MOB,则∠POA 的度数为 ;
②∠BON-∠POA的度数为 .
答案解析
1 、选择题
【考点】相反数.
【分析】只有符号不同的两个数叫做互为相反数,由此即可得到答案.
解:2的相反数是﹣2.
故选:A.
【点评】本题考查相反数,关键是掌握相反数的定义.
【考点】等式的性质.
【分析】的两边同时乘以或除以同一个不为0数或字母,等式仍成立,可得答案.
解:A.左边乘以,右边乘以,故A错误;
B、左边乘以2,右边乘以,故B错误;
C、左边加(2x+1),右边加1,故C错误;
D、两边都加2,故D正确;
故选:D.
【点评】本题主要考查了等式的基本性质,等式的两边同时加上或减去同一个数或字母,等式仍成立;等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.
【考点】点、线、面、体
【分析】根据每一个几何体的特征判断即可.
解:A.可以旋转形成圆台;
B.可以旋转形成球;
C.可以旋转形成圆柱;
D.可以旋转形成圆锥;
故选:A.
【点评】本题考查了点、线、面、体,熟练掌握每一个几何体的特征是解题的关键.
【考点】科学记数法—表示较大的数..
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解:将62200万用科学记数法表示为6.22×108.
故选C
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
【考点】总体、个体、样本、样本容量.
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
解:为了解某校七年级500名学生身高情况,从中抽取了50名学生进行检测,这50名学生的身高是总体的一个样本,
故选:D.
【点评】本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
【考点】有理数的加法.
【分析】根据异号两数相加,取绝对值较大的数的符号,再用较大的绝对值减去较小的绝对值,可得答案.
解:原式=+(4﹣3)=1.
故选:C.
【点评】此题主要考查了有理数加法,正确掌握运算法则是解题关键。
【考点】一元一次方程的应用-配套问题
【分析】根据安排x台机械挖土,则有(30-x)台机械运土,x台机械挖土的总数为3xm3,则(30-x)台机械运土总数为2(30-x)m3,进而得出方程.
解:设安排x台机械挖土,则有(30-x)台机械运土,x台机械挖土的总数为3xm3,则(30-x)台机械运土总数为2(30-x)m3,
根据挖出的土等于运走的土,得:3x=2(30-x).
故选:D.
【点评】此题主要考查了由实际问题抽象出一元一次方程,找出题目蕴含的数量关系是解决问题的关键.
【考点】条形统计图,扇形统计图
【分析】根据类型的条形统计图和扇形统计图信息可判断选项;利用乘以可判断选项;利用类型的人数除以样本总人数可判断选项;利用类型所在百分比乘以样本总人数即可判断选项.
解:,则样本容量为400,选项A说法正确;
,则选项B说法正确;
,则选项C说法错误;
(人),则选项D说法正确;
故选:C.
【点评】本题考查了条形统计图和扇形统计图的信息关联,熟练掌握统计调查的相关知识是解题关键.
【考点】角的计算.
【分析】解答此题的关键是分清两块三角板的锐角度数的度数分别是多少,然后对应着4个选项再进行组合,看看可能画出的角的度数是多少即可.
解:两块三角板的锐角度数分别为:30°,60°;45°,45°
用一块三角板的45°角和另一块三角板的30°角组合可画出15°、75°角,
用一块三角板的直角和和另一块三角板的45°角组合可画出135°角,
无论两块三角板怎么组合也不能画出55°角.
故选B.
【点评】此题主要考查学生对角的计算这一知识点的理解和掌握,解答此题的关键是分清两块三角板的锐角度数的度数分别是多少,比较简单,属于基础题.
【考点】多项式
【分析】先观察多项式的项数,再确定每项的次数,最高次项的次数就是多项式的次数.
解:多项式x2﹣2xy3﹣y﹣1有四项,最高次项﹣2xy3的次数为四,是四次四项式.
故选:C.
【点评】本题考查了多项式的项和次数定义.多项式中每个单项式叫做多项式的项,这些单项式中的最高次数,就是这个多项式的次数.
【考点】探索规律
【分析】根据题目中各个式子的变化规律为n+(n+1)+(n+2)+…+(3n-2)=(2n-1)2,可以判断各个选项中的等式是否成立,从而可以解答本题.
解:由题意可得:1008+1009+…+3022+(3023+3024+3025)=()2+9072=20152+9072≠20162.故选项A错误.
1009+1010+…+3025+3026=()2+3026=20172+3026.故选项B错误.
1009+1010+…+3025=()2=20172.故选项C正确.
1010+1011+…+3029=()2+3029=20192+3029.故选项D错误.
故选C.
【点评】本题考查了有理数的混合运算、规律型:数字的变化类,解答本题的关键是明确题意,发现各个式子的变化规律,可以判断各个选项中的等式是否成立.
【考点】线段的和差,数轴
【分析】设运动时间为t秒,根据题意可知AP=3t,BQ=t,AB=2,然后分类讨论:①当动点P、Q在点O左侧运动时,②当动点P、Q运动到点O右侧时,利用各线段之间的和、差关系即可解答.
解:设运动时间为t秒,由题意可知: AP=3t, BQ=t,
AB=|-6-(-2)|=4,BO=|-2-0|=2,
①当动点P、Q在点O左侧运动时,
PQ=AB-AP+BQ=4-3t+t=2(2-t),
∵OQ= BO- BQ=2-t,
∴PQ= 2OQ ;
②当动点P、Q运动到点O右侧时,
PQ=AP-AB-BQ=3t-4-t=2(t-2),
∵OQ=BQ- BO=t-2,
∴PQ= 2OQ,
综上所述,在运动过程中,线段PQ的长度始终是线段OQ的长的2倍,
即PQ= 2OQ一定成立.
故选:A.
【点评】本题考查了数轴上的动点问题及数轴上两点间的距离,解题时注意分类讨论的运用.
1 、填空题
【考点】解一元一次方程
【分析】将方程移项,然后再将系数化为1即可求得一元一次方程的解.
解:将方程移项得,
2x=2,
系数化为1得,
x=1.
故答案为:1.
【点评】此题主要考查学生对解一元一次方程这一知识点的理解和掌握,此题比较简单,属于基础题
【考点】频数(率)分布直方图
【分析】根据题意和直方图中的数据可以求得成绩为“优良”(80分及以上)的学生人数,本题得以解决.
解:由直方图可得,
成绩为“优良”(80分及以上)的学生有:60+30=90(人),
故答案为:90.
【点评】本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
【考点】绝对值。有理数的混合运算
【分析】根据绝对值的性质求出x的值,再根据有理数的加法运算法则判断出x、y的对应情况,然后代入计算即可得解.
解:∵,
∴,
∵,,
∴,
∴.
故答案为:-4.
【点评】本题考查有理数的加法、绝对值、有理数的混合运算,解题的关键是能根据题目中的信息确定x、y的值.
【考点】同类项,合并同类项
【分析】运用整体思想,将(2a+3)看作一个整体,(2a+3)2+6(2a+3)2=7(2a+3)2.
解:将(2a+3)看作一个整体,化简(2a+3)2+6(2a+3)2=7(2a+3)2
故答案为:7(2a+3)2
【点评】本题考核知识点:合并同类项. 解题关键点:运用整体思想进行化简.
【考点】一元一次方程的应用-配套问题
【分析】设用xkg面粉制作大月饼,则利用(440﹣x)kg制作小月饼,根据题意得到2×小月饼的块数=6×大月饼的块数,依此列出方程.
解:设用xkg面粉制作大月饼,则利用(440﹣x)kg制作小月饼,根据题意得出:
,
解得:x=200,
则440﹣200=220(kg).
所以÷2=8000(盒)
故答案是:8000.
【点评】此题考察一元一次方程的实际应用,正确理解题意是解题的关键,此题找到大小月饼的数量关系即2×小月饼的块数=6×大月饼的块数,设出未知数依据题意列出方程即可得到答案.
【考点】数轴,线段中点
【分析】先根据数轴的定义、线段中点的定义分别求出点表示的数,再归纳类推出一般规律,由此即可得.
解:由题意得:点表示的数为
点表示的数为
点表示的数为
点表示的数为
归纳类推得:点表示的数为(n为正整数)
则点表示的数为
故答案为:.
【点评】本题考查了数轴的定义、线段中点的定义,根据点表示的数,正确归纳类推出一般规律是解题关键.
1 、解答题
【考点】有理数的混合运算.
【分析】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解:原式=﹣1+6××=﹣1+1=0.
【点评】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.
【考点】解一元一次方程
【分析】(1)移项合并后化系数为1即可.
(2)先去括号,然后再进行移项合并.
(3)按解一元一次方程的一般步骤进行解答即可.
(4)此题比较麻烦,要根据步骤一步一步的进行.
解:(1)解:移项合并同类项得,10x=10,
系数化为得,x=1;
(2)解:去括号得,6-2x=-4x-20,
移项合并同类项得,2x=-26,
系数化为1得,x=-13;
(3)解:去分母得,3(x-7)-4(5x+8)=12,
去括号得,3x-21-20x-32=12,
移项合并同类项得,-17x=65,
系数化为1得,x= ;
(4)解:去括号得,2x-x+x-=x-,
去分母得,24x-6x+3x-3=8x-8,
移项合并同类项得,13x=-5,
系数化为1得,x=-.
【点评】本题考查解一元一次方程的知识,题目难度不大,但是出错率很高,是失分率很高的一类题目,同学们要在按步骤解答的基础上更加细心的解答.
【考点】整式的加减—化简求值
【分析】本题考查了整式的加减、去括号法则两个考点.先按照去括号法则去掉整式中的小括号,再合并整式中的同类项即可.
解:原式=(﹣x2+5x+4)+(5x﹣4+2x2)
=﹣x2+5x+4+5x﹣4+2x2=x2+10x
=x(x+10).
∵x=﹣2,
∴原式=﹣16.
【点评】解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.然后代入求值即可.
【考点】整式的加减.
【分析】根据题意可得出A的值,再计算A﹣B即可.
解:∵A+B=9x2﹣2x+7,B=x2+3x﹣2,
∴A=9x2﹣2x+7﹣(x2+3x﹣2)
=9x2﹣2x+7﹣x2﹣3x+2
=8x2﹣5x+9,
∴A﹣B=8x2﹣5x+9﹣(x2+3x﹣2)
=8x2﹣5x+9﹣x2﹣3x+2
=7x2﹣8x+11.
【考点】用样本估计总体;频数(率)分布表;频数(率)分布直方图
【分析】(1)根据百分比=计算即可;
(2)求出a组人数,画出直方图即可;
(3)根据平均数的定义计算即可;
(4)利用样本估计总体的思想解决问题即可;
解:(1)由题意c=18÷0.36=50,
∴a=50×0.2=10,b==0.28,
故答案为10,0.28,50.
(2)频数分布表直方图如图所示.
(3)所有被调查学生课外阅读的平均本数==6.4(本)
(4)该校八年级共有1200名学生,该校八年级学生课外阅读7本及以上的人数有1200×=528(名).
【点评】本题考查频数分布直方图、扇形统计图、样本估计总体等知识,解题的关键是熟练掌握基本概念,灵活运用所学知识解决问题,属于中考常考题型.
【考点】一元一次方程的应用-方案选择
【分析】(1)设1号车有x个学生,则2号车有(104-x)个学生,根据购票总费用=1号车购票费用+2号车购票费用即可得出关于x的一元一次方程,解之即可得出结论;
(2)求出购买104张票的总钱数,将其与1240做差即可得出结论;
(3)分别求出购买48张门票以及购买51张门票的总钱数,比较后即可得出结论.
解:(1)设1号车有x个学生,则2号车有(104﹣x)个学生,
根据题意得:13x+11(104﹣x)=1240,
解得:x=48,
∴104﹣x=56.
答:1号车有48个学生,2号车有56个学生.
(2)1240﹣9×104=304(元).
答:如果两车联合起来,作为一个团体购票,可省304元钱.
(3)51×11=561(元),48×13=624(元),
∴561<624,
∴如果1号车单独组织去游园,购买51张门票最省钱.
【点评】本题考查了一元一次方程的应用,解题的关键是:(1)根据购票总费用=1号车购票费用+2号车购票费用列出关于x的一元一次方程;(2)根据总价=单价×数量求出购买104张门票的总钱数;(3)根据总价=单价×数量分别求出购买48张门票以及购买51张门票的总钱数.
【考点】线段的和差,线段的中点,数轴,一元一次方程的应用
【分析】(1)由数轴两点距离求法AB=12-(-6)=18;设线段AB的中点为E,由线段中点得AE=BE=,由距离求法OE=OB-EB=3;
(2)根据点C的位置进行分类考虑①当点 C 在 AB 之间时, ②当点 C 在点 B 右侧时,设设点C表示的数为x,③当点C在点A左侧时,根据 AC-3BC=6 列方程解之即可.
(1)点 A在数轴上表示的数是-6,点 B在数轴上表示的数是12,
AB=12-(-6)=12+6=18,
设线段AB的中点为E,
则AE=BE=,
OE=OB-EB=12-9=3,
线段AB的中点表示的数是3,
故答案为:18;3 ;
(2)①当点 C 在 AB 之间时,设点C表示的数为x,则 AC=x+6,BC=12-x,
∵AC-3BC=6,
x+6-3(12-x)=6 ,
解答 x=9,
点 C 表示的数为 9 ,
②当点 C 在点 B 右侧时,设设点C表示的数为x,则 AC=x+6,BC= x -12,
∵AC-3BC=6 ,
x+6-3(x-12)=6 ,
解答 x=18,
点 C 表示的数为 18,
③当点C在点A左侧时,AC
【点评】本题考查数轴两点间距离,线段中点,利用线段和差列简单方程,会解方程,会根据点的位置分类讨论是解题关键.
【考点】余角和补角,角的计算
【分析】(1)根据∠POB=∠MOP-∠AOB代入数据即可求出结论;
(2)根据∠PON=180°-∠MOP可算出∠PON的度数,根据OB平分∠PON即可求出∠POB的度数,再通过角的计算可得出∠AOP=60°,结合∠MOP=130°即可得出∠AOM;
(3)①根据OP 所在的直线平分∠MOB,可得出∠MOB=100°,从而可求出∠BON=80°,根据∠BOA=90°求出∠AON=10°,根据∠POA=∠PON-∠AON可得结论;
②设∠AON=x°,则∠BON=90°-x°,∠POA=50°-x°,二者做差即可得出结论.
解:(1)∠POB=∠MOP-∠AOB=130°-90°=40°.
(2)∵∠MON是平角,∠MOP=130゜,
∴∠PON=∠MON-∠MOP=180゜-130゜=50゜
∵OB 平分∠PON,
∴∠BOP=∠PON=25゜
∵∠AOB=90゜,
∴∠AOP=∠AOB-∠BOP=90゜-25゜=65゜
∴∠MOA=∠MOP-∠AOP=130゜-65゜=65゜;
(3)①如图,OE是PO的延长线,
∵∠MOP=130゜
∴∠MOE=50゜
∵OE是∠MOB的平分线,
∴∠MOB=100゜,
∴∠BON=80゜
∵∠AOB=90゜
∴∠AON=∠AOB-∠BON=90゜-80゜=10゜
∴∠POA=∠PON-∠AON=50゜-10゜=40゜;
②设∠AON=x°,则∠BON=90°-x°,∠POA=50°-x°,
∴∠BON-∠POA=(90°-x°)-(50°-x°)=40°.
【点评】本题考查了余角和补角以及角的计算,通过角的计算找出各角之间的关系是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
