2023-2024学年人教版数学九年级下册 26.1.2反比例函数的图像和性质随堂训练 (含答案)
文档属性
| 名称 | 2023-2024学年人教版数学九年级下册 26.1.2反比例函数的图像和性质随堂训练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 378.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 16:57:37 | ||
图片预览

文档简介
26.1.2反比例函数的图像和性质
一、单选题
1.某函数图象刚经过(1,1),该函数的解析式可以是( )
A. B. C. D.
2.点A(-1,1)是反比例函数的图象上一点,则m的值为( )
A.0 B.-2 C.-1 D.1
3.在反比例函数y=﹣图象上有三个点A(-1,y1)、B(-2,y2)、C(1,y3),则下列结论正确的是( )
A.y3<y2<y1 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
4.直线y=ax+b与双曲线y=的图象,如图所示,则( )
A.a>0,b>0,c>0 B.a<0,b<0,c<0
C.a<0,b>0,c>0 D.a<0,b<0,c>0
5.已知反比例函数的图象如图所示,若点P的坐标为,则k的值可能为( )
A.3 B.6 C.7 D.8
6.如图,函数与函数的图象相交于点,,,.若,则x的取值范围是( )
A.或 B.或
C.或 D.或
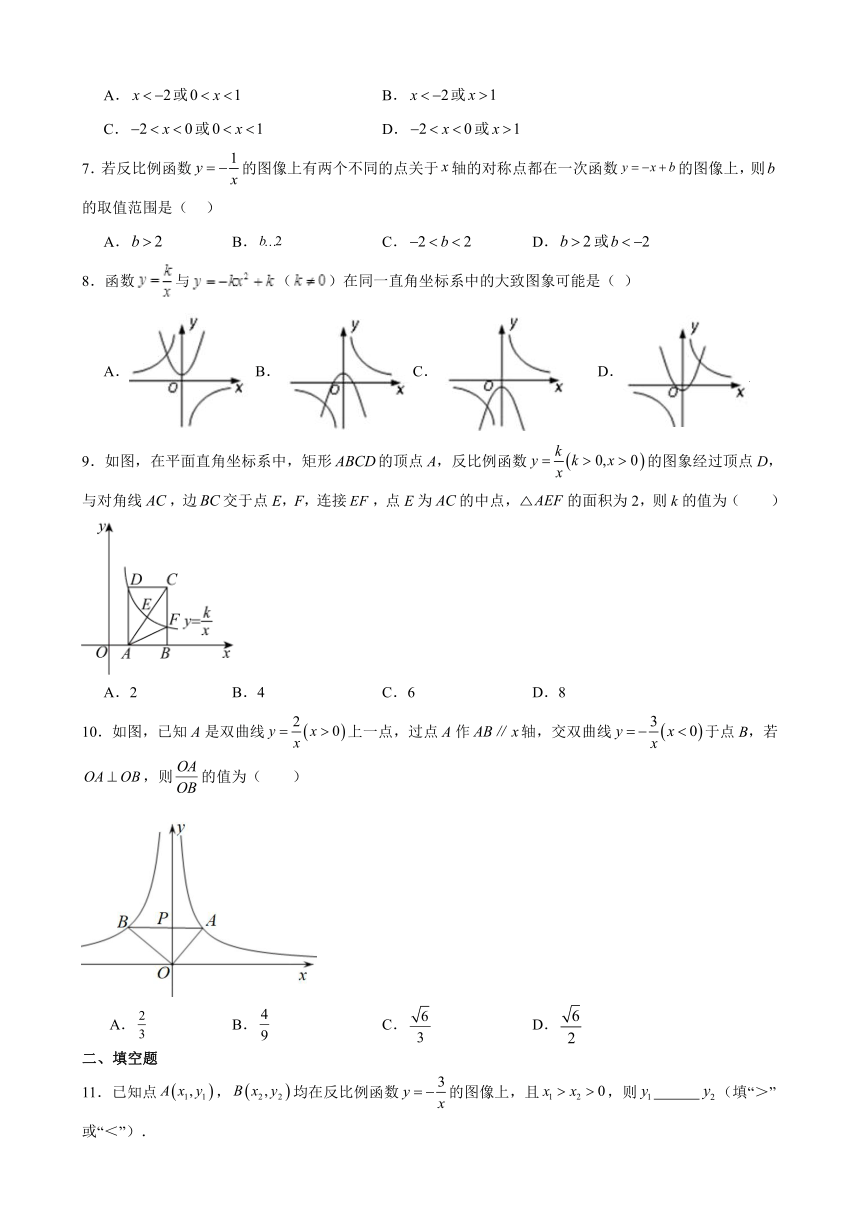
7.若反比例函数的图像上有两个不同的点关于轴的对称点都在一次函数的图像上,则的取值范围是( )
A. B. C. D.或
8.函数与()在同一直角坐标系中的大致图象可能是( )
A.B.C. D.
9.如图,在平面直角坐标系中,矩形的顶点A,反比例函数的图象经过顶点D,与对角线,边交于点E,F,连接,点E为的中点,的面积为2,则k的值为( )
A.2 B.4 C.6 D.8
10.如图,已知A是双曲线上一点,过点A作轴,交双曲线于点B,若,则的值为( )
A. B. C. D.
二、填空题
11.已知点,均在反比例函数的图像上,且,则 (填“>”或“<”).
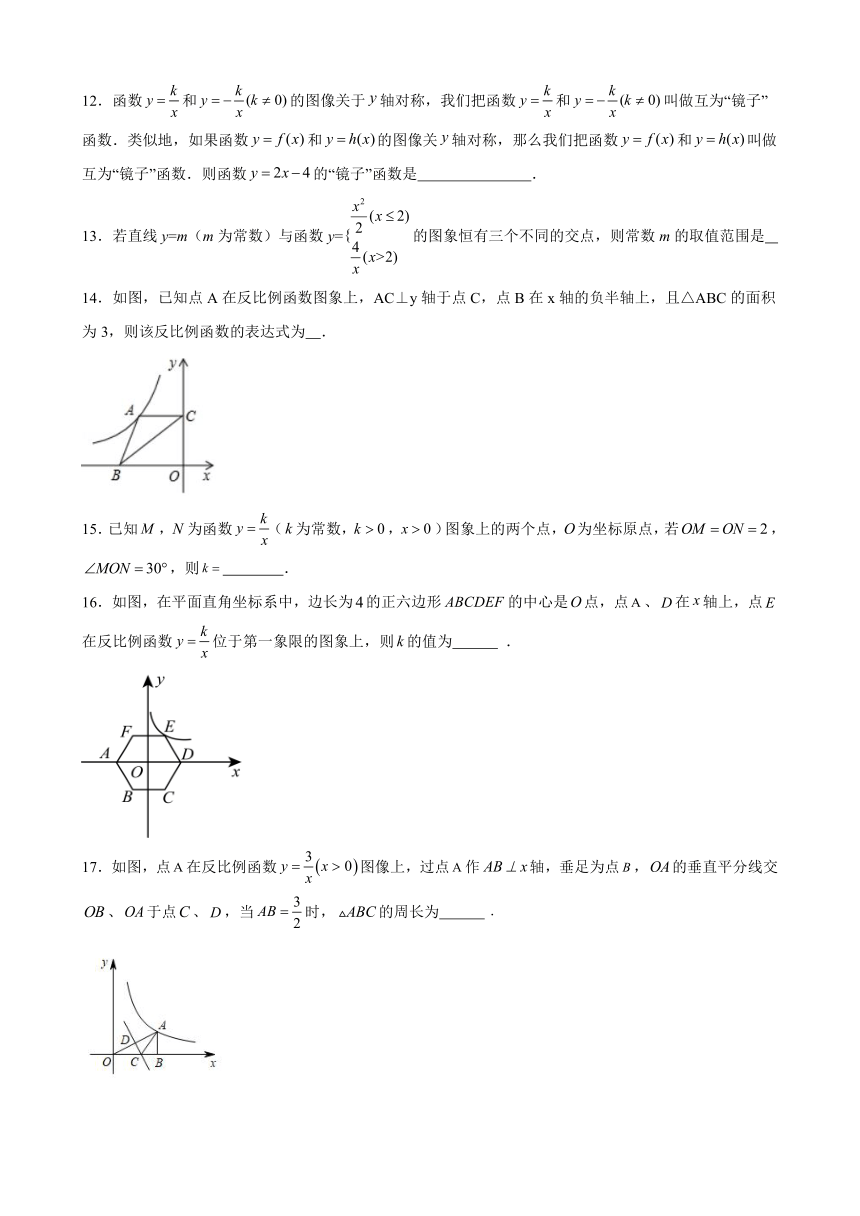
12.函数和的图像关于轴对称,我们把函数和叫做互为“镜子”函数.类似地,如果函数和的图像关轴对称,那么我们把函数和叫做互为“镜子”函数.则函数的“镜子”函数是 .
13.若直线y=m(m为常数)与函数y=的图象恒有三个不同的交点,则常数m的取值范围是
14.如图,已知点A在反比例函数图象上,AC⊥y轴于点C,点B在x轴的负半轴上,且△ABC的面积为3,则该反比例函数的表达式为 .
15.已知,为函数(为常数,,)图象上的两个点,为坐标原点,若,,则 .
16.如图,在平面直角坐标系中,边长为的正六边形的中心是点,点、在轴上,点在反比例函数位于第一象限的图象上,则的值为 .
17.如图,点在反比例函数图像上,过点作轴,垂足为点,的垂直平分线交、于点、,当时,的周长为 ﹒
三、解答题
18.已知,反比例函数图象经过点
(1)求这个反比例函数的解析式;
(2)这个函数的图象位于哪些象限;
(3)随的增大如何变化.
19.一定质量的二氧化碳,它的密度ρ与体积V之间成反比例函数关系,其图象如图所示.求ρ与V之间的函数表达式.
20.如图,在平面直角坐标系中,一次函数与反比例函数(m为常数,且)的图象交于点,.
(1)求反比例函数的解析式;
(2)连接,,求的面积.
21.如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=在第一象限内的图象交于点B,连接BO,若S△OBC=1,tan∠BOC=,求k2的值.
22.如图,已知一次函数的图象与轴相交于点,与反比例函数的图象相交于,两点.
(1 )求一次函数和反比例函数的表达式;
(2 )点是反比例函数的图象上的点,过点作轴的平行线与一次函数的图象相交于点,连接,求的面积.
参考答案:
1.A
2.C
3.A
4.C
5.A
6.D
7.D
8.B
9.C
10.C
11.>
12.
13.0<m<2.
14.y=﹣
15.
16.
17.3.5
18.(1);(2)第一,三象限;(3)在每个象限内随的增大而减小.
19.
20.(1)(2)
21.k2=3
22.(1);;(2)的面积为.
一、单选题
1.某函数图象刚经过(1,1),该函数的解析式可以是( )
A. B. C. D.
2.点A(-1,1)是反比例函数的图象上一点,则m的值为( )
A.0 B.-2 C.-1 D.1
3.在反比例函数y=﹣图象上有三个点A(-1,y1)、B(-2,y2)、C(1,y3),则下列结论正确的是( )
A.y3<y2<y1 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
4.直线y=ax+b与双曲线y=的图象,如图所示,则( )
A.a>0,b>0,c>0 B.a<0,b<0,c<0
C.a<0,b>0,c>0 D.a<0,b<0,c>0
5.已知反比例函数的图象如图所示,若点P的坐标为,则k的值可能为( )
A.3 B.6 C.7 D.8
6.如图,函数与函数的图象相交于点,,,.若,则x的取值范围是( )
A.或 B.或
C.或 D.或
7.若反比例函数的图像上有两个不同的点关于轴的对称点都在一次函数的图像上,则的取值范围是( )
A. B. C. D.或
8.函数与()在同一直角坐标系中的大致图象可能是( )
A.B.C. D.
9.如图,在平面直角坐标系中,矩形的顶点A,反比例函数的图象经过顶点D,与对角线,边交于点E,F,连接,点E为的中点,的面积为2,则k的值为( )
A.2 B.4 C.6 D.8
10.如图,已知A是双曲线上一点,过点A作轴,交双曲线于点B,若,则的值为( )
A. B. C. D.
二、填空题
11.已知点,均在反比例函数的图像上,且,则 (填“>”或“<”).
12.函数和的图像关于轴对称,我们把函数和叫做互为“镜子”函数.类似地,如果函数和的图像关轴对称,那么我们把函数和叫做互为“镜子”函数.则函数的“镜子”函数是 .
13.若直线y=m(m为常数)与函数y=的图象恒有三个不同的交点,则常数m的取值范围是
14.如图,已知点A在反比例函数图象上,AC⊥y轴于点C,点B在x轴的负半轴上,且△ABC的面积为3,则该反比例函数的表达式为 .
15.已知,为函数(为常数,,)图象上的两个点,为坐标原点,若,,则 .
16.如图,在平面直角坐标系中,边长为的正六边形的中心是点,点、在轴上,点在反比例函数位于第一象限的图象上,则的值为 .
17.如图,点在反比例函数图像上,过点作轴,垂足为点,的垂直平分线交、于点、,当时,的周长为 ﹒
三、解答题
18.已知,反比例函数图象经过点
(1)求这个反比例函数的解析式;
(2)这个函数的图象位于哪些象限;
(3)随的增大如何变化.
19.一定质量的二氧化碳,它的密度ρ与体积V之间成反比例函数关系,其图象如图所示.求ρ与V之间的函数表达式.
20.如图,在平面直角坐标系中,一次函数与反比例函数(m为常数,且)的图象交于点,.
(1)求反比例函数的解析式;
(2)连接,,求的面积.
21.如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=在第一象限内的图象交于点B,连接BO,若S△OBC=1,tan∠BOC=,求k2的值.
22.如图,已知一次函数的图象与轴相交于点,与反比例函数的图象相交于,两点.
(1 )求一次函数和反比例函数的表达式;
(2 )点是反比例函数的图象上的点,过点作轴的平行线与一次函数的图象相交于点,连接,求的面积.
参考答案:
1.A
2.C
3.A
4.C
5.A
6.D
7.D
8.B
9.C
10.C
11.>
12.
13.0<m<2.
14.y=﹣
15.
16.
17.3.5
18.(1);(2)第一,三象限;(3)在每个象限内随的增大而减小.
19.
20.(1)(2)
21.k2=3
22.(1);;(2)的面积为.
