7.1.2 平面直角坐标系(一)教学设计(表格式)2023-2024学年人教版七年级数学下册
文档属性
| 名称 | 7.1.2 平面直角坐标系(一)教学设计(表格式)2023-2024学年人教版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 110.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 18:43:05 | ||
图片预览

文档简介
7.1.2平面直角坐标系(一)
课题:7.1.2 平面直角坐标系(一) 上课时间
教学目标 1.使学生了解点的坐标的意义,认识平面直角坐标系,理解平面直角坐标系的意义,会正确建立平面直角坐标系,并会用坐标表示平面直角坐标系内的点。 2.经历坐标概念的形成,渗透对应关系,提高学生的数感。 3.认识到直角坐标系是解决平面实际问题的重要工具。 4.使学生体验数学来源于生活并服务于生活的理念。
教学重点:平面直角坐标系和点的坐标。
教学难点:根据点的位置写出点的坐标,根据点的坐标描出点的位置。
课型课时:新授课,1课时
教学手段:现代课堂教学手段
教学方法:创设情境法
教 学 设 计 二次备课
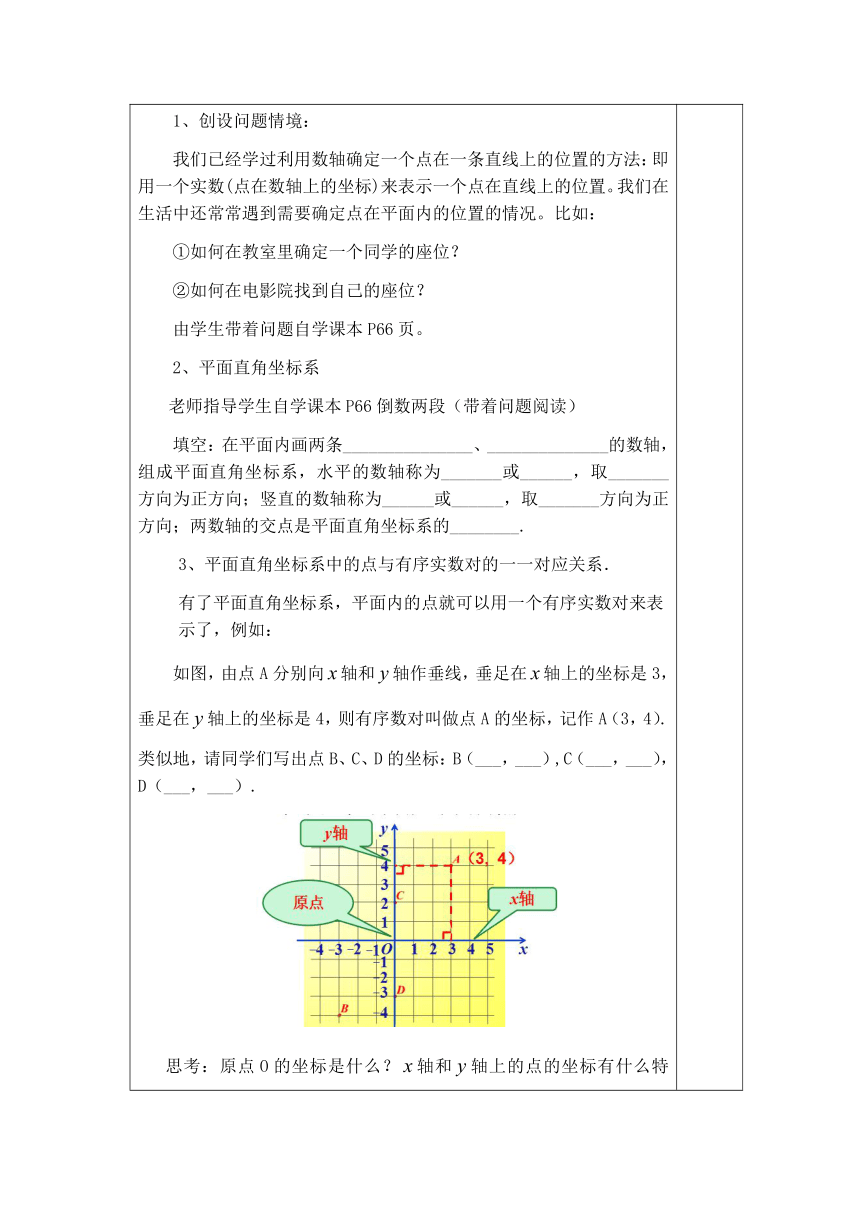
一、课前三分钟 二、复习引入 引导学生回忆(学生自学课本P65页): 1.什么是数轴?(规定了原点,正方向及单位长度的直线) 2.数轴上的点与实数间的关系是什么? (一一对应关系,即数轴上每一个点的位置都能用一个实数表示,反之,任何一个实数在数轴上都有唯一的一个点和它对应,这个实数叫做这个点在数轴上的坐标)。 3.介绍坐标概念。 三、探究新知 1、创设问题情境: 我们已经学过利用数轴确定一个点在一条直线上的位置的方法:即用一个实数(点在数轴上的坐标)来表示一个点在直线上的位置。我们在生活中还常常遇到需要确定点在平面内的位置的情况。比如: ①如何在教室里确定一个同学的座位? ②如何在电影院找到自己的座位? 由学生带着问题自学课本P66页。 2、平面直角坐标系 老师指导学生自学课本P66倒数两段(带着问题阅读) 填空:在平面内画两条_______________、______________的数轴,组成平面直角坐标系,水平的数轴称为_______或______,取_______方向为正方向;竖直的数轴称为______或______,取_______方向为正方向;两数轴的交点是平面直角坐标系的________. 3、平面直角坐标系中的点与有序实数对的一一对应关系. 有了平面直角坐标系,平面内的点就可以用一个有序实数对来表示了,例如: 如图,由点A分别向轴和轴作垂线,垂足在轴上的坐标是3,垂足在轴上的坐标是4,则有序数对叫做点A的坐标,记作A(3,4).类似地,请同学们写出点B、C、D的坐标:B(___,___),C(___,___),D(___,___). 思考:原点O的坐标是什么?轴和轴上的点的坐标有什么特点? 归纳总结:可以看出,原点O的坐标为(0,0);轴上的点的纵坐标为0,例如(0,0),(-1,0)…;轴上的点的横坐标为0,例如(0,1),(0,-1),…. 4、建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个部分(如图所示),每个部分叫做象限,分别叫做第一象限、第二象限、第三象限和第四象限. 注意:坐标轴上的点不属于任何象限! 总结:平面直角坐标系中任一点M,有一对有序实数(x,y)和它对应;反之,对任意实数对(x,y),在坐标系中都有一个点和它对应,这就是说平面内所有的点与有序实数对是一一对应的. 例 在平面直角坐标系中描出下列各点: A(4,5),B(-2,3),C(-4,-1),D(0,-4) 教师带领学生分析并讲解。 四、草原练兵 以军事演练为案例,引导学生巩固新知,将班级划分为平面直角坐标系,选几名学生说出自己的位置坐标,并在坐标系中描述出来。 五、课堂小结 本节课我们主要认识了平面直角坐标系,用有序数对表示点的坐标及将点在平面直角坐标系中表示出来!
作业 布置 必做 课本P68练习第1题、第2题
选做 习题7.1第1题
板书 设计 7.1.2 平面直角坐标系(一) 一、课前三分钟 二、复习引入 数轴及数轴上的点与实数的关系 三、探究新知 平面直角坐标系及象限 四、草原练兵 五、课堂小结及作业布置
课后 反思
课题:7.1.2 平面直角坐标系(一) 上课时间
教学目标 1.使学生了解点的坐标的意义,认识平面直角坐标系,理解平面直角坐标系的意义,会正确建立平面直角坐标系,并会用坐标表示平面直角坐标系内的点。 2.经历坐标概念的形成,渗透对应关系,提高学生的数感。 3.认识到直角坐标系是解决平面实际问题的重要工具。 4.使学生体验数学来源于生活并服务于生活的理念。
教学重点:平面直角坐标系和点的坐标。
教学难点:根据点的位置写出点的坐标,根据点的坐标描出点的位置。
课型课时:新授课,1课时
教学手段:现代课堂教学手段
教学方法:创设情境法
教 学 设 计 二次备课
一、课前三分钟 二、复习引入 引导学生回忆(学生自学课本P65页): 1.什么是数轴?(规定了原点,正方向及单位长度的直线) 2.数轴上的点与实数间的关系是什么? (一一对应关系,即数轴上每一个点的位置都能用一个实数表示,反之,任何一个实数在数轴上都有唯一的一个点和它对应,这个实数叫做这个点在数轴上的坐标)。 3.介绍坐标概念。 三、探究新知 1、创设问题情境: 我们已经学过利用数轴确定一个点在一条直线上的位置的方法:即用一个实数(点在数轴上的坐标)来表示一个点在直线上的位置。我们在生活中还常常遇到需要确定点在平面内的位置的情况。比如: ①如何在教室里确定一个同学的座位? ②如何在电影院找到自己的座位? 由学生带着问题自学课本P66页。 2、平面直角坐标系 老师指导学生自学课本P66倒数两段(带着问题阅读) 填空:在平面内画两条_______________、______________的数轴,组成平面直角坐标系,水平的数轴称为_______或______,取_______方向为正方向;竖直的数轴称为______或______,取_______方向为正方向;两数轴的交点是平面直角坐标系的________. 3、平面直角坐标系中的点与有序实数对的一一对应关系. 有了平面直角坐标系,平面内的点就可以用一个有序实数对来表示了,例如: 如图,由点A分别向轴和轴作垂线,垂足在轴上的坐标是3,垂足在轴上的坐标是4,则有序数对叫做点A的坐标,记作A(3,4).类似地,请同学们写出点B、C、D的坐标:B(___,___),C(___,___),D(___,___). 思考:原点O的坐标是什么?轴和轴上的点的坐标有什么特点? 归纳总结:可以看出,原点O的坐标为(0,0);轴上的点的纵坐标为0,例如(0,0),(-1,0)…;轴上的点的横坐标为0,例如(0,1),(0,-1),…. 4、建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个部分(如图所示),每个部分叫做象限,分别叫做第一象限、第二象限、第三象限和第四象限. 注意:坐标轴上的点不属于任何象限! 总结:平面直角坐标系中任一点M,有一对有序实数(x,y)和它对应;反之,对任意实数对(x,y),在坐标系中都有一个点和它对应,这就是说平面内所有的点与有序实数对是一一对应的. 例 在平面直角坐标系中描出下列各点: A(4,5),B(-2,3),C(-4,-1),D(0,-4) 教师带领学生分析并讲解。 四、草原练兵 以军事演练为案例,引导学生巩固新知,将班级划分为平面直角坐标系,选几名学生说出自己的位置坐标,并在坐标系中描述出来。 五、课堂小结 本节课我们主要认识了平面直角坐标系,用有序数对表示点的坐标及将点在平面直角坐标系中表示出来!
作业 布置 必做 课本P68练习第1题、第2题
选做 习题7.1第1题
板书 设计 7.1.2 平面直角坐标系(一) 一、课前三分钟 二、复习引入 数轴及数轴上的点与实数的关系 三、探究新知 平面直角坐标系及象限 四、草原练兵 五、课堂小结及作业布置
课后 反思
