2023-2024学年 北师大版 八年级数学下册1.2直角三角形 直角三角形全等的判定(HL)-讲练课件-(共28张PPT)
文档属性
| 名称 | 2023-2024学年 北师大版 八年级数学下册1.2直角三角形 直角三角形全等的判定(HL)-讲练课件-(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 619.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
第一章 三角形的证明
第6课 直角三角形全等的判定(HL)
数学(RS版) 八年级下册
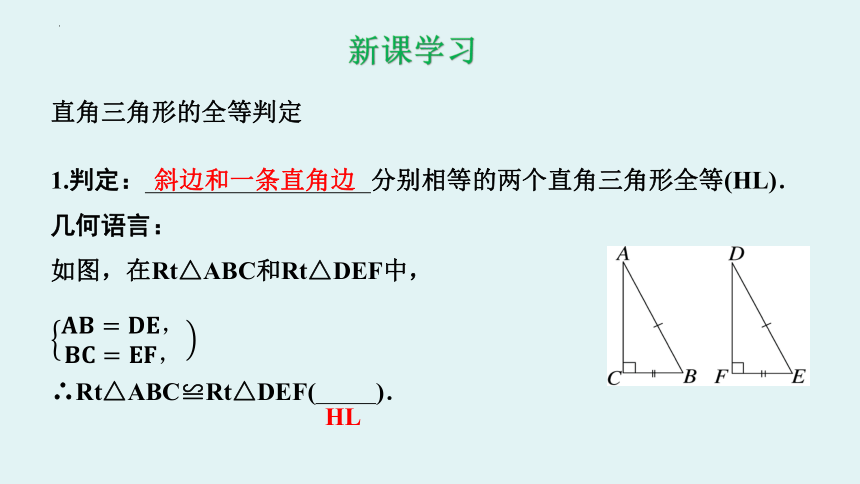
直角三角形的全等判定
1.判定: 分别相等的两个直角三角形全等(HL).
几何语言:
如图,在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF( ).
斜边和一条直角边
HL
新课学习
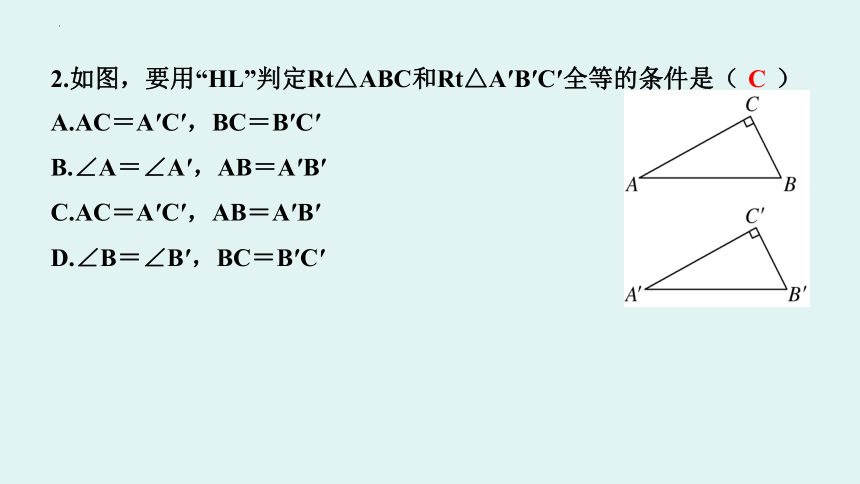
2.如图,要用“HL”判定Rt△ABC和Rt△A′B′C′全等的条件是( C )
A.AC=A′C′,BC=B′C′
B.∠A=∠A′,AB=A′B′
C.AC=A′C′,AB=A′B′
D.∠B=∠B′,BC=B′C′
C
例1 如图,AC⊥BC于点C,BD⊥AD于点D,AC=BD.求证:∠ABC
=∠BAD.
证明:∵AC⊥BC,BD⊥AD,
∴∠ACB=∠BDA=90°.
在Rt△ABC和Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL).
∴∠ABC=∠BAD.
3.如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边
BC,EF在同一条直线上,斜边AC,DF交于点G,且BF=CE,AC=DF.
求证:GF=GC.
证明:∵BF=CE,∴BF+FC=CE+FC.∴BC=EF.
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL).
∴∠ACB=∠DFE.∴GF=GC.
直角三角形全等的性质与判定的应用
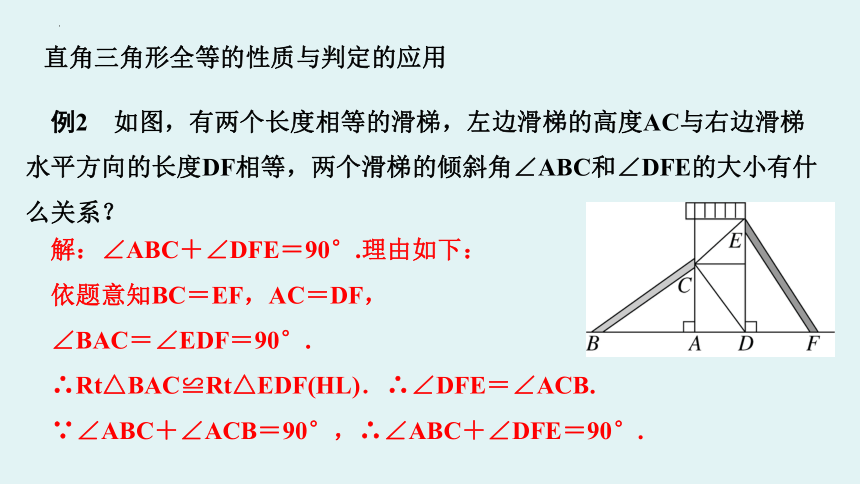
例2 如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯
水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什
么关系?
解:∠ABC+∠DFE=90°.理由如下:
依题意知BC=EF,AC=DF,
∠BAC=∠EDF=90°.
∴Rt△BAC≌Rt△EDF(HL).∴∠DFE=∠ACB.
∵∠ABC+∠ACB=90°,∴∠ABC+∠DFE=90°.
4.如图,点C是路段AB的中点,小明和小红两人从点C同时出发,以相
同的速度分别沿两条直线行走,并同时到达D,E两地,并且DA⊥AB于
点A,EB⊥AB于点B.此时小明到路段AB的距离是50米,则小红到路段
AB的距离是多少米?
解:∵DA⊥AB,EB⊥AB,
∴△ADC和△BEC为直角三角形.
∵点C是路段AB的中点,∴AC=BC.
∵小明和小红同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,∴CD=CE.
∴Rt△ADC≌Rt△BEC(HL).∴BE=AD=50米.
答:小红到路段AB的距离是50米.
1.如图,点P是∠BAC内一点,PE⊥AC于点E,PF⊥AB于点F,
PE=PF,则能直接得到△PEA≌△PFA的理由是( A )
A.HL B.ASA
C.AAS D.SAS
A
基础巩固
2.用尺规作图,不能作出唯一一种直角三角形的是( B )
A.已知两条直角边
B.已知两个锐角
C.已知一直角边和该直角边所对的一锐角
D.已知斜边和一直角边
B
3.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=
( B )
A.40° B.50° C.60° D.75°
B
4.一题多问 如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°.
(1)若∠A=∠D,BC=EF,则Rt△ABC≌Rt△DEF的依据
是 ;
(2)若∠A=∠D,AC=DF,则Rt△ABC≌Rt△DEF的依据
是 ;
AAS
ASA
(3)若∠A=∠D,AB=DE,则Rt△ABC≌Rt△DEF的依据
是 ;
(4)若AC=DF,CB=FE,则Rt△ABC≌Rt△DEF的依据是 ;
(5)若AC=DF,AB=DE,则Rt△ABC≌Rt△DEF的依据是 .
AAS
SAS
HL
5.如图,CE⊥AB,DF⊥AB,AC=BD,AF=BE.求证:AC∥BD.
证明:∵AF=BE,
∴AF-EF=BE-EF,即AE=BF.
∵CE⊥AB,DF⊥AB,
∴∠AEC=∠BFD=90°.
在Rt△AEC和Rt△BFD中,
∴Rt△AEC≌Rt△BFD(HL).
∴∠A=∠B.∴AC∥BD.
6.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ
=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当
AP= 时,△ABC和△PQA全等.
5或10
7.【教材P35复习题T13变式】如图,AC⊥BC,AD⊥BD,垂足分别
为点C,D,AD=BC,CE⊥AB,DF⊥AB,垂足分别是点E,F.求证:
CE=DF.
证明:∵AC⊥BC,AD⊥BD,
∴∠ACB=∠BDA=90°.
∵BC=AD,AB=BA,∴Rt△ABC≌Rt△BAD(HL).
∴∠CBE=∠DAF.
∵CE⊥AB,DF⊥AB,∴∠CEB=∠DFA=90°.
在△BCE和△ADF中, ∴△BCE≌△ADF(AAS).
∴CE=DF.
1.如图,∠B=∠E=90°,AB=DE,AC=DF,则
△ABC≌△DEF的理由是( D )
A.SAS
B.ASA
C.AAS
D.HL
D
复习训练
2.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定
Rt△ABC和Rt△ABD全等.以下给出的条件适合的是( A )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
3.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若
AC=6 cm,则AE+DE等于( C )
A.4 cm B.5 cm C.6 cm D.7 cm
C
4.如图,AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
( 1 )若以“SAS”为依据,需添加的一个条件为 ;
( 2 )若以“HL”为依据,需添加的一个条件为 .
AB=CD
BC=DA
5.下列三角形:①有两个角等于60°的三角形;②有一个角等于
60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角
形.其中等边三角形是( D )
A.①②③ B.①②④
C.①③④ D.①②③④
D
1.如图,已知AC⊥BD,垂足为点O,AO=CO,AB=CD,则可得
到△AOB≌△COD,理由是( A )
A.HL B.SAS C.ASA D.SSS
A
基础训练
2.如图,在△ABC中,∠C=90°,AD=AC,DE⊥AB于点D.若
∠B=28°,则∠AEC=( B )
A.28° B.59° C.60° D.62°
B
3.如图,在△ABC中,∠BAC=90°,ED⊥BC于点D,AB=
BD,若AC=8,DE=3,则EC的长为 5 .
5
4.【教材P21习题T1变式】如图,点D是△ABC的边BC的中点,
DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.求证:AB=AC.
证明:∵点D是△ABC的边BC的中点,∴BD=CD.
∵DF⊥AB,DE⊥AC,
∴∠BFD=∠CED=90°.
在Rt△BDF和Rt△CDE中,
∴Rt△BDF≌Rt△CDE( HL ).
∴∠B=∠C.∴AB=AC.
5.【教材P34复习题T4变式】如图,CD⊥AB,BE⊥AC,垂足分别
为点D,E,BE与CD相交于点O,连接AO,且∠1=∠2,则下列结论
中:①∠ABC=∠ACB;②△ADO≌△AEO;③△BOD≌△COE;④图
中有四对三角形全等.正确的个数为( C )
A.1个
B.2个
C.3个
D.4个
C
6.如图,已知Rt△ABC中,∠ACB=90°,CA=CB,点D是AC上
一点,点E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试
探索BF与AE有何特殊的位置关系?并说明理由.
解:BF⊥AE.理由如下:
∵∠ACB=90°,点E在BC的延长线上,∴∠ACE=90°.
在Rt△BCD和Rt△ACE中,
∴Rt△BCD≌Rt△ACE( HL ).∴∠CBD=∠CAE.
∵∠ACB=90°,∴∠CBD+∠BDC=90°.
∴∠CAE+∠BDC=90°.
又∠BDC=∠ADF,∴∠CAE+∠ADF=90°.
∴∠AFD=90°,即BF⊥AE.
7.如图,已知P( 2,2 ),点A在x轴正半轴上运动,点B在y轴负半轴
上运动,且PA=PB.
( 1 )求证:PA⊥PB;
( 1 )证明:如图,过点P作PM⊥x轴于点M,
PN⊥y轴于点N,BP交OA于点Q.
∴∠PMA=∠PNB=90°,PM=PN=2.
在Rt△PMA和Rt△PNB中,
∴Rt△PMA≌Rt△PNB( HL ).∴∠PAM=∠PBN.
∵∠PQA+∠PAQ=∠BQO+∠PBN.
∴∠BPA=∠BOA=90°.∴PA⊥PB.
( 2 )若点A( 8,0 ),则点B的坐标为 ( 0,-4 ) ;
( 3 )求OA-OB的值.
( 0,-4 )
( 3 )解:由( 1 ),得△PMA≌△PNB.∴MA=BN.
∴OA-OB=( OM+MA )-( BN-ON )
=OM+ON=4.
第一章 三角形的证明
第6课 直角三角形全等的判定(HL)
数学(RS版) 八年级下册
直角三角形的全等判定
1.判定: 分别相等的两个直角三角形全等(HL).
几何语言:
如图,在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF( ).
斜边和一条直角边
HL
新课学习
2.如图,要用“HL”判定Rt△ABC和Rt△A′B′C′全等的条件是( C )
A.AC=A′C′,BC=B′C′
B.∠A=∠A′,AB=A′B′
C.AC=A′C′,AB=A′B′
D.∠B=∠B′,BC=B′C′
C
例1 如图,AC⊥BC于点C,BD⊥AD于点D,AC=BD.求证:∠ABC
=∠BAD.
证明:∵AC⊥BC,BD⊥AD,
∴∠ACB=∠BDA=90°.
在Rt△ABC和Rt△BAD中,
∴Rt△ABC≌Rt△BAD(HL).
∴∠ABC=∠BAD.
3.如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边
BC,EF在同一条直线上,斜边AC,DF交于点G,且BF=CE,AC=DF.
求证:GF=GC.
证明:∵BF=CE,∴BF+FC=CE+FC.∴BC=EF.
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL).
∴∠ACB=∠DFE.∴GF=GC.
直角三角形全等的性质与判定的应用
例2 如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯
水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什
么关系?
解:∠ABC+∠DFE=90°.理由如下:
依题意知BC=EF,AC=DF,
∠BAC=∠EDF=90°.
∴Rt△BAC≌Rt△EDF(HL).∴∠DFE=∠ACB.
∵∠ABC+∠ACB=90°,∴∠ABC+∠DFE=90°.
4.如图,点C是路段AB的中点,小明和小红两人从点C同时出发,以相
同的速度分别沿两条直线行走,并同时到达D,E两地,并且DA⊥AB于
点A,EB⊥AB于点B.此时小明到路段AB的距离是50米,则小红到路段
AB的距离是多少米?
解:∵DA⊥AB,EB⊥AB,
∴△ADC和△BEC为直角三角形.
∵点C是路段AB的中点,∴AC=BC.
∵小明和小红同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地,∴CD=CE.
∴Rt△ADC≌Rt△BEC(HL).∴BE=AD=50米.
答:小红到路段AB的距离是50米.
1.如图,点P是∠BAC内一点,PE⊥AC于点E,PF⊥AB于点F,
PE=PF,则能直接得到△PEA≌△PFA的理由是( A )
A.HL B.ASA
C.AAS D.SAS
A
基础巩固
2.用尺规作图,不能作出唯一一种直角三角形的是( B )
A.已知两条直角边
B.已知两个锐角
C.已知一直角边和该直角边所对的一锐角
D.已知斜边和一直角边
B
3.如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=
( B )
A.40° B.50° C.60° D.75°
B
4.一题多问 如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°.
(1)若∠A=∠D,BC=EF,则Rt△ABC≌Rt△DEF的依据
是 ;
(2)若∠A=∠D,AC=DF,则Rt△ABC≌Rt△DEF的依据
是 ;
AAS
ASA
(3)若∠A=∠D,AB=DE,则Rt△ABC≌Rt△DEF的依据
是 ;
(4)若AC=DF,CB=FE,则Rt△ABC≌Rt△DEF的依据是 ;
(5)若AC=DF,AB=DE,则Rt△ABC≌Rt△DEF的依据是 .
AAS
SAS
HL
5.如图,CE⊥AB,DF⊥AB,AC=BD,AF=BE.求证:AC∥BD.
证明:∵AF=BE,
∴AF-EF=BE-EF,即AE=BF.
∵CE⊥AB,DF⊥AB,
∴∠AEC=∠BFD=90°.
在Rt△AEC和Rt△BFD中,
∴Rt△AEC≌Rt△BFD(HL).
∴∠A=∠B.∴AC∥BD.
6.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ
=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当
AP= 时,△ABC和△PQA全等.
5或10
7.【教材P35复习题T13变式】如图,AC⊥BC,AD⊥BD,垂足分别
为点C,D,AD=BC,CE⊥AB,DF⊥AB,垂足分别是点E,F.求证:
CE=DF.
证明:∵AC⊥BC,AD⊥BD,
∴∠ACB=∠BDA=90°.
∵BC=AD,AB=BA,∴Rt△ABC≌Rt△BAD(HL).
∴∠CBE=∠DAF.
∵CE⊥AB,DF⊥AB,∴∠CEB=∠DFA=90°.
在△BCE和△ADF中, ∴△BCE≌△ADF(AAS).
∴CE=DF.
1.如图,∠B=∠E=90°,AB=DE,AC=DF,则
△ABC≌△DEF的理由是( D )
A.SAS
B.ASA
C.AAS
D.HL
D
复习训练
2.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定
Rt△ABC和Rt△ABD全等.以下给出的条件适合的是( A )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
3.如图,在△ABC中,∠C=90°,ED⊥AB于点D,BD=BC,若
AC=6 cm,则AE+DE等于( C )
A.4 cm B.5 cm C.6 cm D.7 cm
C
4.如图,AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
( 1 )若以“SAS”为依据,需添加的一个条件为 ;
( 2 )若以“HL”为依据,需添加的一个条件为 .
AB=CD
BC=DA
5.下列三角形:①有两个角等于60°的三角形;②有一个角等于
60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角
形.其中等边三角形是( D )
A.①②③ B.①②④
C.①③④ D.①②③④
D
1.如图,已知AC⊥BD,垂足为点O,AO=CO,AB=CD,则可得
到△AOB≌△COD,理由是( A )
A.HL B.SAS C.ASA D.SSS
A
基础训练
2.如图,在△ABC中,∠C=90°,AD=AC,DE⊥AB于点D.若
∠B=28°,则∠AEC=( B )
A.28° B.59° C.60° D.62°
B
3.如图,在△ABC中,∠BAC=90°,ED⊥BC于点D,AB=
BD,若AC=8,DE=3,则EC的长为 5 .
5
4.【教材P21习题T1变式】如图,点D是△ABC的边BC的中点,
DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.求证:AB=AC.
证明:∵点D是△ABC的边BC的中点,∴BD=CD.
∵DF⊥AB,DE⊥AC,
∴∠BFD=∠CED=90°.
在Rt△BDF和Rt△CDE中,
∴Rt△BDF≌Rt△CDE( HL ).
∴∠B=∠C.∴AB=AC.
5.【教材P34复习题T4变式】如图,CD⊥AB,BE⊥AC,垂足分别
为点D,E,BE与CD相交于点O,连接AO,且∠1=∠2,则下列结论
中:①∠ABC=∠ACB;②△ADO≌△AEO;③△BOD≌△COE;④图
中有四对三角形全等.正确的个数为( C )
A.1个
B.2个
C.3个
D.4个
C
6.如图,已知Rt△ABC中,∠ACB=90°,CA=CB,点D是AC上
一点,点E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试
探索BF与AE有何特殊的位置关系?并说明理由.
解:BF⊥AE.理由如下:
∵∠ACB=90°,点E在BC的延长线上,∴∠ACE=90°.
在Rt△BCD和Rt△ACE中,
∴Rt△BCD≌Rt△ACE( HL ).∴∠CBD=∠CAE.
∵∠ACB=90°,∴∠CBD+∠BDC=90°.
∴∠CAE+∠BDC=90°.
又∠BDC=∠ADF,∴∠CAE+∠ADF=90°.
∴∠AFD=90°,即BF⊥AE.
7.如图,已知P( 2,2 ),点A在x轴正半轴上运动,点B在y轴负半轴
上运动,且PA=PB.
( 1 )求证:PA⊥PB;
( 1 )证明:如图,过点P作PM⊥x轴于点M,
PN⊥y轴于点N,BP交OA于点Q.
∴∠PMA=∠PNB=90°,PM=PN=2.
在Rt△PMA和Rt△PNB中,
∴Rt△PMA≌Rt△PNB( HL ).∴∠PAM=∠PBN.
∵∠PQA+∠PAQ=∠BQO+∠PBN.
∴∠BPA=∠BOA=90°.∴PA⊥PB.
( 2 )若点A( 8,0 ),则点B的坐标为 ( 0,-4 ) ;
( 3 )求OA-OB的值.
( 0,-4 )
( 3 )解:由( 1 ),得△PMA≌△PNB.∴MA=BN.
∴OA-OB=( OM+MA )-( BN-ON )
=OM+ON=4.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
