2023-2024学年 北师大版 八年级数学下册1.3线段垂直平分线 线段垂直平分线的性质与判定-讲练课件-(共30张PPT)
文档属性
| 名称 | 2023-2024学年 北师大版 八年级数学下册1.3线段垂直平分线 线段垂直平分线的性质与判定-讲练课件-(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 498.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 19:10:46 | ||
图片预览










文档简介
(共30张PPT)
第一章 三角形的证明
第7课 线段垂直平分线的性质与判定
数学(RS版) 八年级下册
线段垂直平分线的性质
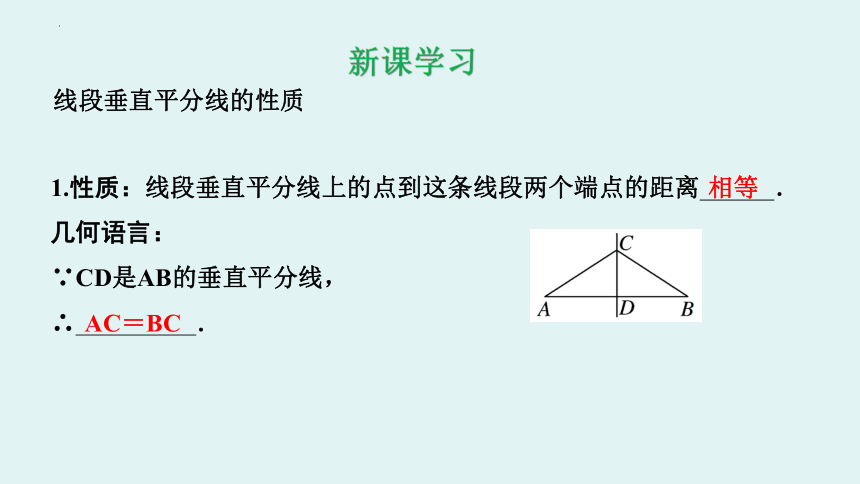
1.性质:线段垂直平分线上的点到这条线段两个端点的距离 .
几何语言:
∵CD是AB的垂直平分线,
∴ .
相等
AC=BC
新课学习
2.如图,CD是AB的垂直平分线,垂足为点D.
(1)AD=________,∠ADC= °,AC= ;
(2)若AD=4,AC=5,则△ABC的周长为 .
BD或(AB)
90
BC
18
例1 如图,AD是BC的垂直平分线,点M是AD上一点.求证:
∠ABM=∠ACM.
证明:∵AD是BC的垂直平分线,
∴AB=AC,MB=MC.
∴∠ABC=∠ACB,∠MBC=∠MCB.
∴∠ABC-∠MBC=∠ACB-∠MCB.
∴∠ABM=∠ACM.
3.如图,在△ABC中,AC的垂直平分线交AC于点D,交BC的延长线于
点E,连接AE,若∠B=50°,∠BAC=21°,求∠CAE的度数.
解:∵DE垂直平分AC,∴EA=EC.
∴∠CAE=∠ECA.
∵∠B=50°,∠BAC=21°,
∴∠ECA=∠B+∠BAC=71°.
∴∠CAE=71°.
线段垂直平分线的判定
4.判定:到一条线段两个端点距离相等的点,在这条线段的
上 .
几何语言:
∵ ,
∴点P在AB的垂直平分线上.
垂直平分
线
AP=BP
5.如图,直线PO与AB交于点O,PA=PB,则下列结论中正确的是
( D )
A.AO=BO
B.PO⊥AB
C.PO是AB的垂直平分线
D.点P在AB的垂直平分线上
D
例2 如图,在△ABC中,AB=AC,点O是△ABC内一点,且OB=
OC.求证:直线AO垂直平分线段BC.
证明:∵AB=AC,
∴点A在线段BC的垂直平分线上.
∵OB=OC,
∴点O在线段BC的垂直平分线上.
∵两点确定一条直线,
∴直线AO垂直平分线段BC.
6.如图,AB=AC,DB=DC,点E是AD延长线上的一点,BE是否与
CE相等?试说明理由.
解:BE=CE.理由如下:
如图,连接BC.∵AB=AC,
∴点A在线段BC的垂直平分线上.
∵DB=DC,∴点D也在线段BC的垂直平分线上.
∵两点确定一条直线,∴AD是线段BC的垂直平分线.
∵点E是AD延长线上的一点,∴BE=CE.
1.如图,线段AC的垂直平分线DE交线段AB于点D,∠A=50°,
则∠BDC=( B )
A.50° B.100°
C.110° D.120°
B
基础巩固
2.如图,在△ABC中,边AC的垂直平分线交AC于点M,交BC于点
N,若AB=3,BC=13,则△ABN的周长是( C )
A.10 B.13
C.16 D.无法确定
C
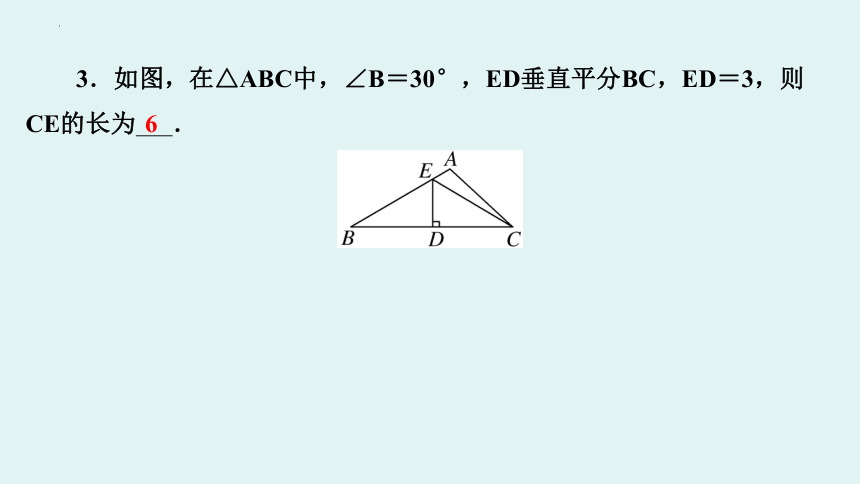
3.如图,在△ABC中,∠B=30°,ED垂直平分BC,ED=3,则
CE的长为 .
6
4.如图,在四边形ABCD中,AB=AD,边BC的垂直平分线MN经
过点A.求证:点A在CD的垂直平分线上.
证明:如图,连接AC.
∵MN垂直平分BC,
∴AB=AC.
∵AB=AD,
∴AC=AD.
∴点A在CD的垂直平分线上.
5.如图,在△ABC中,∠C=90°,∠A=30°.
(1)用尺规作出AB的垂直平分线交AB于点D,交AC于点E;
(2)求证:AE=2CE.
(1)解:如图,DE即为所作.
(2)证明:如图,连接BE.
∵DE垂直平分AB,∴AE=BE.∴∠EBA=∠A=30°.
∵∠ABC=90°-∠A=60°,∴∠CBE=30°.
∵∠C=90°,∴BE=2CE.∴AE=2CE.
6.【拓展题】如图,在△ABC中,若MP和NQ分别垂直平分AB和
AC.
(1)若BC=15,求△APQ的周长;
解:(1)∵MP和NQ分别垂直平分AB,AC,
∴AP=BP,AQ=CQ.
∴△APQ的周长=AP+AQ+PQ=BP+CQ+PQ=BC=15.
(2)若∠BAC=105°,求∠PAQ的度数.
解:(2)∵∠B+∠BAC+∠C=180°,
∴∠B+∠C=180°-∠BAC=180°-105°=75°.
∵MP,NQ分别垂直平分AB和AC,∴AP=BP,AQ=CQ.
∴∠BAP=∠B,∠CAQ=∠C.
∴∠BAP+∠CAQ=∠B+∠C=75°.
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=105°-75°=30°.
1.如图,直线l垂直平分线段AB,点P是l上一点,已知PA=1,则
PB( A )
A.等于1
B.小于1
C.大于1
D.不能确定
A
复习训练
2.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P
一定( D )
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高线上 D.在边AB的垂直平分线上
D
3.如图,在△ABC中,AB的垂直平分线交AC于点D,如果AC=5
cm,BD=3 cm,那么DC的长是( A )
A.2 cm B.3 cm C.4 cm D.5 cm
A
4.如图,在△ABC中,DE垂直平分AC交AB于点E,∠A=30°,
∠ACB=80°,则∠BCE= °.
50
5.如图,AB垂直平分CD,AC=6,BD=4,则四边形ADBC的周
长是 .
20
6.如图,BD平分∠ABC,CD⊥BD,点D为垂足,∠C=55°,则
∠ABC的度数是( D )
A.35°
B.55°
C.60°
D.70°
D
1.如图,直线CD是线段AB的垂直平分线,点P为直线CD上的一
点.已知PA=4,则线段PB的长为 4 .
4
基础训练
2.如图,若AC=AD,BC=BD,则( B )
A.CD垂直平分AB B.AB垂直平分CD
C.CD平分∠ACB D.以上均不对
B
3.如图,AD⊥BC于点D,BD=DC,点C在AE的垂直平分线上,
则AB,AC,CE的长度关系为( D )
A.AB>AC=CE B.AB=AC>CE
C.AB>AC>CE D.AB=AC=CE
D
4.如图,在Rt△ABC中,∠C=90°,DE是AB的垂直平分线,若
∠CAD∶∠DAB=2∶1,则∠B的度数为( B )
A.20° B.22.5° C.25° D.30°
B
5.如图,在△ABC中,∠BAC=90°,AC=8 cm,DE是BC的垂
直平分线,△ABD的周长为14 cm.求BC的长.
解:∵DE是BC的垂直平分线,∴BD=DC.
∵△ABD的周长为14,
∴AB+AD+BD=14.
∴AB+AD+DC=AB+AC=14.
∴AB=14-8=6( cm ).
在Rt△ABC中,由勾股定理,得BC==10( cm ).
6.如图,∠1=∠2,∠3=∠4.求证:AB垂直平分MN.
证明:在△ABM和△ABN中,
∴△ABM≌△ABN( ASA ).
∴AM=AN,BM=BN.
∴点A,B都落在MN的垂直平分线上.
∴AB垂直平分MN.
7.如图,在△ABC中,AB=BC,∠ABC=120°,AB的垂直平分
线DE交AC于点D,连接BD,若AC=12.
( 1 )求证:DB⊥BC;
( 1 )证明:∵AB=BC,∠ABC=120°,
∴∠A=∠C=30°.
∵DE垂直平分AB,∴AD=BD.∴∠ABD=∠A=30°.
∴∠DBC=∠ABC-∠ABD=120°-30°=90°.
∴DB⊥BC.
( 2 )求DB的长.
( 2 )解:由( 1 )可知∠DBC=90°,∠A=∠C=30°.
∴CD=2DB.
∵DE垂直平分AB,∴AD=DB.
∵AD+CD=AC,∴3DB=AC=12.
∴DB=4.
第一章 三角形的证明
第7课 线段垂直平分线的性质与判定
数学(RS版) 八年级下册
线段垂直平分线的性质
1.性质:线段垂直平分线上的点到这条线段两个端点的距离 .
几何语言:
∵CD是AB的垂直平分线,
∴ .
相等
AC=BC
新课学习
2.如图,CD是AB的垂直平分线,垂足为点D.
(1)AD=________,∠ADC= °,AC= ;
(2)若AD=4,AC=5,则△ABC的周长为 .
BD或(AB)
90
BC
18
例1 如图,AD是BC的垂直平分线,点M是AD上一点.求证:
∠ABM=∠ACM.
证明:∵AD是BC的垂直平分线,
∴AB=AC,MB=MC.
∴∠ABC=∠ACB,∠MBC=∠MCB.
∴∠ABC-∠MBC=∠ACB-∠MCB.
∴∠ABM=∠ACM.
3.如图,在△ABC中,AC的垂直平分线交AC于点D,交BC的延长线于
点E,连接AE,若∠B=50°,∠BAC=21°,求∠CAE的度数.
解:∵DE垂直平分AC,∴EA=EC.
∴∠CAE=∠ECA.
∵∠B=50°,∠BAC=21°,
∴∠ECA=∠B+∠BAC=71°.
∴∠CAE=71°.
线段垂直平分线的判定
4.判定:到一条线段两个端点距离相等的点,在这条线段的
上 .
几何语言:
∵ ,
∴点P在AB的垂直平分线上.
垂直平分
线
AP=BP
5.如图,直线PO与AB交于点O,PA=PB,则下列结论中正确的是
( D )
A.AO=BO
B.PO⊥AB
C.PO是AB的垂直平分线
D.点P在AB的垂直平分线上
D
例2 如图,在△ABC中,AB=AC,点O是△ABC内一点,且OB=
OC.求证:直线AO垂直平分线段BC.
证明:∵AB=AC,
∴点A在线段BC的垂直平分线上.
∵OB=OC,
∴点O在线段BC的垂直平分线上.
∵两点确定一条直线,
∴直线AO垂直平分线段BC.
6.如图,AB=AC,DB=DC,点E是AD延长线上的一点,BE是否与
CE相等?试说明理由.
解:BE=CE.理由如下:
如图,连接BC.∵AB=AC,
∴点A在线段BC的垂直平分线上.
∵DB=DC,∴点D也在线段BC的垂直平分线上.
∵两点确定一条直线,∴AD是线段BC的垂直平分线.
∵点E是AD延长线上的一点,∴BE=CE.
1.如图,线段AC的垂直平分线DE交线段AB于点D,∠A=50°,
则∠BDC=( B )
A.50° B.100°
C.110° D.120°
B
基础巩固
2.如图,在△ABC中,边AC的垂直平分线交AC于点M,交BC于点
N,若AB=3,BC=13,则△ABN的周长是( C )
A.10 B.13
C.16 D.无法确定
C
3.如图,在△ABC中,∠B=30°,ED垂直平分BC,ED=3,则
CE的长为 .
6
4.如图,在四边形ABCD中,AB=AD,边BC的垂直平分线MN经
过点A.求证:点A在CD的垂直平分线上.
证明:如图,连接AC.
∵MN垂直平分BC,
∴AB=AC.
∵AB=AD,
∴AC=AD.
∴点A在CD的垂直平分线上.
5.如图,在△ABC中,∠C=90°,∠A=30°.
(1)用尺规作出AB的垂直平分线交AB于点D,交AC于点E;
(2)求证:AE=2CE.
(1)解:如图,DE即为所作.
(2)证明:如图,连接BE.
∵DE垂直平分AB,∴AE=BE.∴∠EBA=∠A=30°.
∵∠ABC=90°-∠A=60°,∴∠CBE=30°.
∵∠C=90°,∴BE=2CE.∴AE=2CE.
6.【拓展题】如图,在△ABC中,若MP和NQ分别垂直平分AB和
AC.
(1)若BC=15,求△APQ的周长;
解:(1)∵MP和NQ分别垂直平分AB,AC,
∴AP=BP,AQ=CQ.
∴△APQ的周长=AP+AQ+PQ=BP+CQ+PQ=BC=15.
(2)若∠BAC=105°,求∠PAQ的度数.
解:(2)∵∠B+∠BAC+∠C=180°,
∴∠B+∠C=180°-∠BAC=180°-105°=75°.
∵MP,NQ分别垂直平分AB和AC,∴AP=BP,AQ=CQ.
∴∠BAP=∠B,∠CAQ=∠C.
∴∠BAP+∠CAQ=∠B+∠C=75°.
∴∠PAQ=∠BAC-(∠BAP+∠CAQ)=105°-75°=30°.
1.如图,直线l垂直平分线段AB,点P是l上一点,已知PA=1,则
PB( A )
A.等于1
B.小于1
C.大于1
D.不能确定
A
复习训练
2.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P
一定( D )
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高线上 D.在边AB的垂直平分线上
D
3.如图,在△ABC中,AB的垂直平分线交AC于点D,如果AC=5
cm,BD=3 cm,那么DC的长是( A )
A.2 cm B.3 cm C.4 cm D.5 cm
A
4.如图,在△ABC中,DE垂直平分AC交AB于点E,∠A=30°,
∠ACB=80°,则∠BCE= °.
50
5.如图,AB垂直平分CD,AC=6,BD=4,则四边形ADBC的周
长是 .
20
6.如图,BD平分∠ABC,CD⊥BD,点D为垂足,∠C=55°,则
∠ABC的度数是( D )
A.35°
B.55°
C.60°
D.70°
D
1.如图,直线CD是线段AB的垂直平分线,点P为直线CD上的一
点.已知PA=4,则线段PB的长为 4 .
4
基础训练
2.如图,若AC=AD,BC=BD,则( B )
A.CD垂直平分AB B.AB垂直平分CD
C.CD平分∠ACB D.以上均不对
B
3.如图,AD⊥BC于点D,BD=DC,点C在AE的垂直平分线上,
则AB,AC,CE的长度关系为( D )
A.AB>AC=CE B.AB=AC>CE
C.AB>AC>CE D.AB=AC=CE
D
4.如图,在Rt△ABC中,∠C=90°,DE是AB的垂直平分线,若
∠CAD∶∠DAB=2∶1,则∠B的度数为( B )
A.20° B.22.5° C.25° D.30°
B
5.如图,在△ABC中,∠BAC=90°,AC=8 cm,DE是BC的垂
直平分线,△ABD的周长为14 cm.求BC的长.
解:∵DE是BC的垂直平分线,∴BD=DC.
∵△ABD的周长为14,
∴AB+AD+BD=14.
∴AB+AD+DC=AB+AC=14.
∴AB=14-8=6( cm ).
在Rt△ABC中,由勾股定理,得BC==10( cm ).
6.如图,∠1=∠2,∠3=∠4.求证:AB垂直平分MN.
证明:在△ABM和△ABN中,
∴△ABM≌△ABN( ASA ).
∴AM=AN,BM=BN.
∴点A,B都落在MN的垂直平分线上.
∴AB垂直平分MN.
7.如图,在△ABC中,AB=BC,∠ABC=120°,AB的垂直平分
线DE交AC于点D,连接BD,若AC=12.
( 1 )求证:DB⊥BC;
( 1 )证明:∵AB=BC,∠ABC=120°,
∴∠A=∠C=30°.
∵DE垂直平分AB,∴AD=BD.∴∠ABD=∠A=30°.
∴∠DBC=∠ABC-∠ABD=120°-30°=90°.
∴DB⊥BC.
( 2 )求DB的长.
( 2 )解:由( 1 )可知∠DBC=90°,∠A=∠C=30°.
∴CD=2DB.
∵DE垂直平分AB,∴AD=DB.
∵AD+CD=AC,∴3DB=AC=12.
∴DB=4.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
