2023-2024学年 北师大版 八年级数学下册1.4 角平分线 角平分线的性质与判定 课件(共33张PPT)
文档属性
| 名称 | 2023-2024学年 北师大版 八年级数学下册1.4 角平分线 角平分线的性质与判定 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 19:54:04 | ||
图片预览











文档简介
(共33张PPT)
第一章 三角形的证明
第9课 角平分线的性质与判定
数学(RS版) 八年级下册
角平分线的性质
1.性质:角平分线上的点到这个角的两边的距离 .
几何语言:
∵ , , ,
∴ .
相等
AP平分∠BAC
PB⊥AB
PC⊥AC
PB=PC
新课学习
2.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点
D,DE⊥BC于点E,若AD=3,DC=5,则DE= ,CE= .
3
4
例1 如图,在△ABC中,AD是它的角平分线,且BD=CD,
DE⊥AB,DF⊥AC,垂足分别为点E,F.求证:EB=FC.
证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°.
在Rt△BED和Rt△CFD中,
∴Rt△BED≌Rt△CFD(HL).
∴EB=FC.
3.如图,CD⊥AB于点D,BE⊥AC于点E,CD,BE交于点O,连接
AO,∠1=∠2.求证:OB=OC.
证明:∵∠1=∠2,∴AO是∠BAC的平分线.
∵CD⊥AB,BE⊥AC,
∴DO=EO,∠BDO=∠CEO=90°.
在△BDO和△CEO中,
∴△BDO≌△CEO(ASA).
∴OB=OC.
角平分线的判定
4.判定:在一个角的内部,到角的两边距离 的点在这个角的平分
线上.
几何语言:
∵PB⊥AB, , ,
∴AP平分∠BAC,即∠BAP=∠CAP.
相等
PC⊥AC
PB=PC
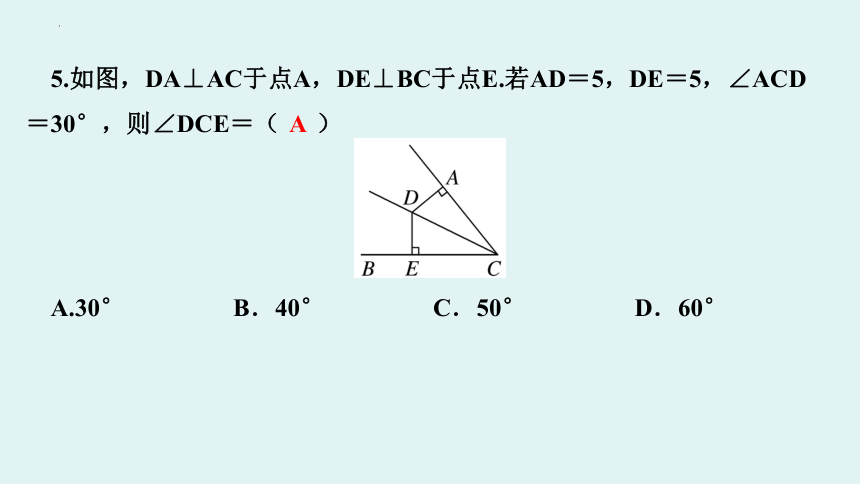
5.如图,DA⊥AC于点A,DE⊥BC于点E.若AD=5,DE=5,∠ACD
=30°,则∠DCE=( A )
A.30° B.40° C.50° D.60°
A
例2 如图,在△ABC中,点D是BC的中点,DE⊥AB,DF⊥AC,垂
足分别是点E,F,BE=CF.求证:AD平分∠BAC.
证明:∵点D是BC的中点,∴DB=DC.
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°.
∵BE=CF,∴Rt△DEB≌Rt△DFC(HL).
∴DE=DF.
∵DE⊥AB,DF⊥AC,∴AD平分∠BAC.
6.如图,在△ABC中,∠B=60°,点D为AC边上的点,DE⊥AB,
DF⊥BC,垂足分别为点E,F,且DE=DF= .求线段BE的长.
解:如图,连接BD.
∵DE=DF,DE⊥AB,DF⊥BC,
∴BD平分∠ABC.
∴∠ABD=∠ABC=×60°=30°.
在Rt△BDE中,DE=,∠DBE=30°,
∴BD=2DE=2.∴BE==3.
1.如图,DB⊥AB,DC⊥AC,垂足分别为点B,C,AD平分
∠BAC,BD=2,∠BAC=80°,则DC= ,∠ADC= °.
2
50
基础巩固
2.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为点A,
B.下列结论中不一定成立的是( D )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
D
3.如图,在Rt△ABC中,∠A=90°,∠C=30°,BD平分∠ABC
且与AC边交于点D,AC=3,则点D到边BC的距离是 .
1
4.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点
D,CD=2,点Q为AB上一动点,则DQ的最小值为( A )
A.2 B.2 C. D.
A
5.如图,在Rt△ABC中,∠C=90°,点D是AC上一点,DE⊥AB
于点E,且DE=DC.
(1)求证:BD平分∠ABC;
(2)若∠A=38°,求∠DBC的度数.
(1)证明:∵∠C=90°,∴DC⊥BC.
∵DE⊥AB,DE=DC,∴BD平分∠ABC.
(2)解:∵∠C=90°,∠A=38°,∴∠ABC=52°.
由(1)知,BD平分∠ABC.∴∠DBC=∠ABC=26°.
6.如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交
BC于点D,DE⊥AB,垂足为点E.若DE=1,则BC=________ .
2+
7.如图,一把直尺压住射线OB,另一把完全一样的直尺压住射线
OA并且与第一把直尺交于点P,小明说:“射线OP就是∠AOB的平分
线.”这样说的依据是
.
在一个角的内部,到角的两边距离相等的点在这
个角的平分线上
8.如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC
于点F,AB=8 cm,AC=6 cm,△ABC的面积为21 cm2,求DE的长度.
解:∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF.
∵S△ABC=S△ABD+S△ACD
= AB·DE+ AC·DF=21,
AB=8 cm,AC=6 cm,
∴×(8+6)·DE=21.
∴DE=3.
9.如图,已知AB=AC,DE⊥AB交AB的延长线于点E,DF⊥AC交
AC的延长线于点F,DE=DF.求证:BD=CD.
证明:如图,连接AD.
∵DE=DF,DE⊥AB,DF⊥AC,∴AD平分∠BAC.
∴∠1=∠2.
在△ADB和△ADC中,
∴△ADB≌△ADC(SAS).
∴BD=CD.
1.如图,观察尺规作图痕迹,下列说法错误的是( C )
A.OE是∠AOB的平分线 B.OC=OD
C.点C,D到OE的距离不相等 D.∠AOE=∠BOE
C
复习训练
2.如图,PD⊥AB,PE⊥AC,垂足分别为点D,E,且PD=PE,若
∠BAP=20°,则∠BAC=( D )
A.10° B.20° C.30° D.40°
D
3.如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则
点C到射线OA的距离为 .
3
4.如图,已知∠CDA=∠CBA=90°,且CD=CB,则点C
在 的平分线上,点A在 的平分线上.
∠BAD
∠DCB
循环复习
5.如图,DE是△ABC中AC边上的垂直平分线,若BC=8 cm,AB
=10 cm,则△EBC的周长为( B )
A.16 cm B.18 cm C.26 cm D.28 cm
B
1.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明
∠AOC=∠BOC的依据是( A )
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
基础训练
2.如图,在△ABC中,∠C=90°,DE⊥AB于点E,CD=DE,若
∠CBD=26°,则∠A的度数为( D )
A.40° B.34° C.36° D.38°
D
3.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交
于点P,过点P作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离
为 4 .
4
4.在9×7的网格中,∠AOB的位置如图所示,则到∠AOB两边距离
相等的点是( A )
A.点M B.点N C.点P D.点Q
A
5.如图,OC是∠AOB的平分线,AC⊥OB于点D,BC⊥OA于点E.
求证:AC=BC.
证明:∵OC平分∠AOB,CE⊥OA,CD⊥OB,
∴CE=CD.
在△ACE和△BCD中,
∵∠AEC=∠BDC=90°,CE=CD,∠ACE=∠BCD,
∴△ACE≌△BCD( ASA ).
∴AC=BC.
6.已知:如图,锐角三角形ABC的两条高BD,CE相交于点O,且
OB=OC.
( 1 )求证:△ABC是等腰三角形;
( 1 )证明:∵CE,BD是△ABC的高,
∴∠BEC=∠CDB=90°.
∵∠EOB=∠DOC,∴∠ABD=∠ACE.
∵OB=OC,∴∠OBC=∠OCB.
∴∠ABD+∠OBC=∠ACE+∠OCB,即∠ABC=∠ACB.
∴AB=AC.∴△ABC是等腰三角形.
( 2 )判断点O是否在∠BAC的平分线上,并说明理由.
( 2 )解:点O在∠BAC的平分线上.理由如下:
∵∠BEO=∠CDO=90°,∠BOE=∠COD,
OB=OC,∴△BOE≌△COD( AAS ).
∴OE=OD.
∵OD⊥AC,OE⊥AB,∴点O在∠BAC的平分线上.
7.如图,在四边形ABDC中,∠D=∠B=90°,点O为BD的中点,
且AO平分∠BAC.
( 1 )求证:CO平分∠ACD;
证明:( 1 )如图,过点O作OE⊥AC于点E.
∵∠B=90°,∴OB⊥AB.
∵OE⊥AC,AO平分∠BAC,∴OB=OE.
∵点O为BD的中点,∴OB=OD.∴OE=OD.
∵∠D=90°,∴OD⊥CD.
又OE⊥AC,∴CO平分∠ACD.
( 2 )求证:OA⊥OC;
( 2 )在Rt△ABO和Rt△AEO中,
∴Rt△ABO≌Rt△AEO( HL ).∴∠AOB=∠AOE.
在Rt△CDO和Rt△CEO中,
∴Rt△CDO≌Rt△CEO( HL ).∴∠COD=∠COE.
∵∠AOE+∠AOB+∠COE+∠COD=180°,
∴2∠AOE+2∠COE=180°.
∴∠AOC=∠AOE+∠COE=×180°=90°.∴OA⊥OC.
( 3 )求证:AB+CD=AC.
( 3 )∵Rt△ABO≌Rt△AEO,∴AB=AE.
∵Rt△CDO≌Rt△CEO,∴CD=CE.
∵AE+CE=AC,∴AB+CD=AC.
第一章 三角形的证明
第9课 角平分线的性质与判定
数学(RS版) 八年级下册
角平分线的性质
1.性质:角平分线上的点到这个角的两边的距离 .
几何语言:
∵ , , ,
∴ .
相等
AP平分∠BAC
PB⊥AB
PC⊥AC
PB=PC
新课学习
2.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点
D,DE⊥BC于点E,若AD=3,DC=5,则DE= ,CE= .
3
4
例1 如图,在△ABC中,AD是它的角平分线,且BD=CD,
DE⊥AB,DF⊥AC,垂足分别为点E,F.求证:EB=FC.
证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°.
在Rt△BED和Rt△CFD中,
∴Rt△BED≌Rt△CFD(HL).
∴EB=FC.
3.如图,CD⊥AB于点D,BE⊥AC于点E,CD,BE交于点O,连接
AO,∠1=∠2.求证:OB=OC.
证明:∵∠1=∠2,∴AO是∠BAC的平分线.
∵CD⊥AB,BE⊥AC,
∴DO=EO,∠BDO=∠CEO=90°.
在△BDO和△CEO中,
∴△BDO≌△CEO(ASA).
∴OB=OC.
角平分线的判定
4.判定:在一个角的内部,到角的两边距离 的点在这个角的平分
线上.
几何语言:
∵PB⊥AB, , ,
∴AP平分∠BAC,即∠BAP=∠CAP.
相等
PC⊥AC
PB=PC
5.如图,DA⊥AC于点A,DE⊥BC于点E.若AD=5,DE=5,∠ACD
=30°,则∠DCE=( A )
A.30° B.40° C.50° D.60°
A
例2 如图,在△ABC中,点D是BC的中点,DE⊥AB,DF⊥AC,垂
足分别是点E,F,BE=CF.求证:AD平分∠BAC.
证明:∵点D是BC的中点,∴DB=DC.
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°.
∵BE=CF,∴Rt△DEB≌Rt△DFC(HL).
∴DE=DF.
∵DE⊥AB,DF⊥AC,∴AD平分∠BAC.
6.如图,在△ABC中,∠B=60°,点D为AC边上的点,DE⊥AB,
DF⊥BC,垂足分别为点E,F,且DE=DF= .求线段BE的长.
解:如图,连接BD.
∵DE=DF,DE⊥AB,DF⊥BC,
∴BD平分∠ABC.
∴∠ABD=∠ABC=×60°=30°.
在Rt△BDE中,DE=,∠DBE=30°,
∴BD=2DE=2.∴BE==3.
1.如图,DB⊥AB,DC⊥AC,垂足分别为点B,C,AD平分
∠BAC,BD=2,∠BAC=80°,则DC= ,∠ADC= °.
2
50
基础巩固
2.如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为点A,
B.下列结论中不一定成立的是( D )
A.PA=PB B.PO平分∠APB
C.OA=OB D.AB垂直平分OP
D
3.如图,在Rt△ABC中,∠A=90°,∠C=30°,BD平分∠ABC
且与AC边交于点D,AC=3,则点D到边BC的距离是 .
1
4.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点
D,CD=2,点Q为AB上一动点,则DQ的最小值为( A )
A.2 B.2 C. D.
A
5.如图,在Rt△ABC中,∠C=90°,点D是AC上一点,DE⊥AB
于点E,且DE=DC.
(1)求证:BD平分∠ABC;
(2)若∠A=38°,求∠DBC的度数.
(1)证明:∵∠C=90°,∴DC⊥BC.
∵DE⊥AB,DE=DC,∴BD平分∠ABC.
(2)解:∵∠C=90°,∠A=38°,∴∠ABC=52°.
由(1)知,BD平分∠ABC.∴∠DBC=∠ABC=26°.
6.如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交
BC于点D,DE⊥AB,垂足为点E.若DE=1,则BC=________ .
2+
7.如图,一把直尺压住射线OB,另一把完全一样的直尺压住射线
OA并且与第一把直尺交于点P,小明说:“射线OP就是∠AOB的平分
线.”这样说的依据是
.
在一个角的内部,到角的两边距离相等的点在这
个角的平分线上
8.如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC
于点F,AB=8 cm,AC=6 cm,△ABC的面积为21 cm2,求DE的长度.
解:∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF.
∵S△ABC=S△ABD+S△ACD
= AB·DE+ AC·DF=21,
AB=8 cm,AC=6 cm,
∴×(8+6)·DE=21.
∴DE=3.
9.如图,已知AB=AC,DE⊥AB交AB的延长线于点E,DF⊥AC交
AC的延长线于点F,DE=DF.求证:BD=CD.
证明:如图,连接AD.
∵DE=DF,DE⊥AB,DF⊥AC,∴AD平分∠BAC.
∴∠1=∠2.
在△ADB和△ADC中,
∴△ADB≌△ADC(SAS).
∴BD=CD.
1.如图,观察尺规作图痕迹,下列说法错误的是( C )
A.OE是∠AOB的平分线 B.OC=OD
C.点C,D到OE的距离不相等 D.∠AOE=∠BOE
C
复习训练
2.如图,PD⊥AB,PE⊥AC,垂足分别为点D,E,且PD=PE,若
∠BAP=20°,则∠BAC=( D )
A.10° B.20° C.30° D.40°
D
3.如图,OC为∠AOB的平分线,CM⊥OB,OC=5,OM=4,则
点C到射线OA的距离为 .
3
4.如图,已知∠CDA=∠CBA=90°,且CD=CB,则点C
在 的平分线上,点A在 的平分线上.
∠BAD
∠DCB
循环复习
5.如图,DE是△ABC中AC边上的垂直平分线,若BC=8 cm,AB
=10 cm,则△EBC的周长为( B )
A.16 cm B.18 cm C.26 cm D.28 cm
B
1.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明
∠AOC=∠BOC的依据是( A )
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
基础训练
2.如图,在△ABC中,∠C=90°,DE⊥AB于点E,CD=DE,若
∠CBD=26°,则∠A的度数为( D )
A.40° B.34° C.36° D.38°
D
3.如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交
于点P,过点P作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离
为 4 .
4
4.在9×7的网格中,∠AOB的位置如图所示,则到∠AOB两边距离
相等的点是( A )
A.点M B.点N C.点P D.点Q
A
5.如图,OC是∠AOB的平分线,AC⊥OB于点D,BC⊥OA于点E.
求证:AC=BC.
证明:∵OC平分∠AOB,CE⊥OA,CD⊥OB,
∴CE=CD.
在△ACE和△BCD中,
∵∠AEC=∠BDC=90°,CE=CD,∠ACE=∠BCD,
∴△ACE≌△BCD( ASA ).
∴AC=BC.
6.已知:如图,锐角三角形ABC的两条高BD,CE相交于点O,且
OB=OC.
( 1 )求证:△ABC是等腰三角形;
( 1 )证明:∵CE,BD是△ABC的高,
∴∠BEC=∠CDB=90°.
∵∠EOB=∠DOC,∴∠ABD=∠ACE.
∵OB=OC,∴∠OBC=∠OCB.
∴∠ABD+∠OBC=∠ACE+∠OCB,即∠ABC=∠ACB.
∴AB=AC.∴△ABC是等腰三角形.
( 2 )判断点O是否在∠BAC的平分线上,并说明理由.
( 2 )解:点O在∠BAC的平分线上.理由如下:
∵∠BEO=∠CDO=90°,∠BOE=∠COD,
OB=OC,∴△BOE≌△COD( AAS ).
∴OE=OD.
∵OD⊥AC,OE⊥AB,∴点O在∠BAC的平分线上.
7.如图,在四边形ABDC中,∠D=∠B=90°,点O为BD的中点,
且AO平分∠BAC.
( 1 )求证:CO平分∠ACD;
证明:( 1 )如图,过点O作OE⊥AC于点E.
∵∠B=90°,∴OB⊥AB.
∵OE⊥AC,AO平分∠BAC,∴OB=OE.
∵点O为BD的中点,∴OB=OD.∴OE=OD.
∵∠D=90°,∴OD⊥CD.
又OE⊥AC,∴CO平分∠ACD.
( 2 )求证:OA⊥OC;
( 2 )在Rt△ABO和Rt△AEO中,
∴Rt△ABO≌Rt△AEO( HL ).∴∠AOB=∠AOE.
在Rt△CDO和Rt△CEO中,
∴Rt△CDO≌Rt△CEO( HL ).∴∠COD=∠COE.
∵∠AOE+∠AOB+∠COE+∠COD=180°,
∴2∠AOE+2∠COE=180°.
∴∠AOC=∠AOE+∠COE=×180°=90°.∴OA⊥OC.
( 3 )求证:AB+CD=AC.
( 3 )∵Rt△ABO≌Rt△AEO,∴AB=AE.
∵Rt△CDO≌Rt△CEO,∴CD=CE.
∵AE+CE=AC,∴AB+CD=AC.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
