第一章 三角形的证明 章末复习 讲练课件(共48张PPT)
文档属性
| 名称 | 第一章 三角形的证明 章末复习 讲练课件(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 20:24:15 | ||
图片预览







文档简介
(共48张PPT)
第一章 三角形的证明
第11课 三角形的证明章末复习
数学(RS版) 八年级下册
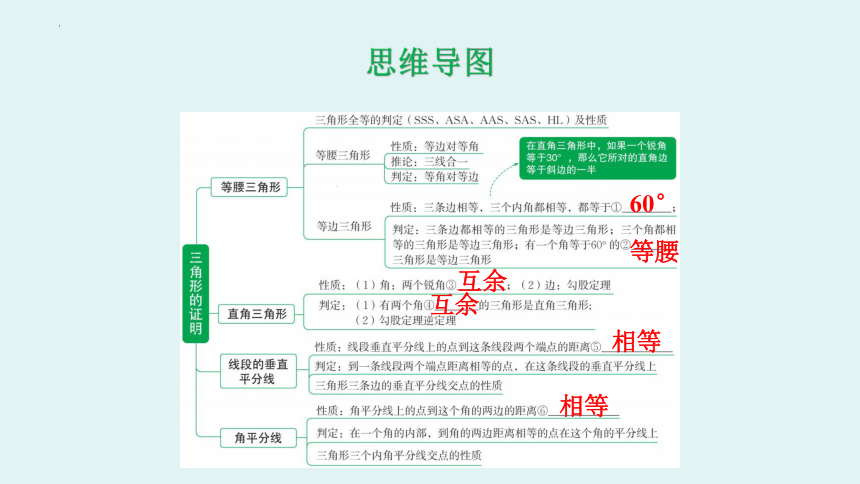
60°
等腰
互余
互余
相等
相等
思维导图
等腰三角形
1.如图,在△ABC中,AB=AC.
(1)若∠A=50°,则∠C= ;
(2)若∠B=50°,则∠A= .
65°
80°
高频考点
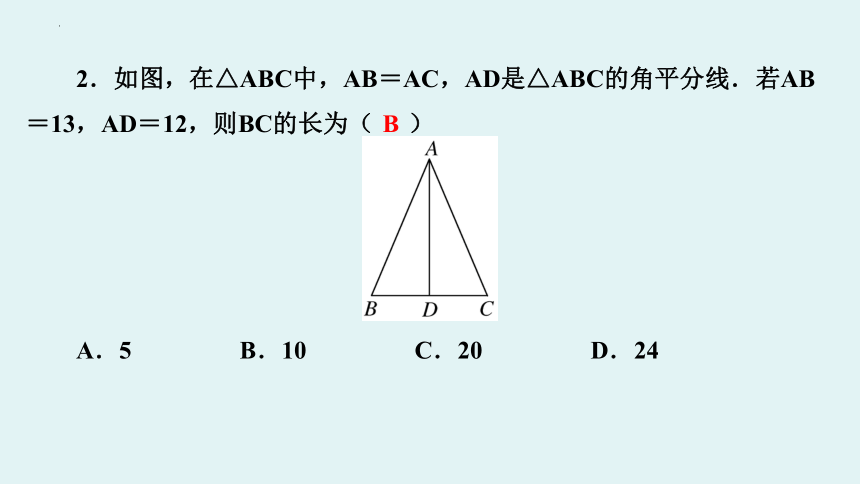
2.如图,在△ABC中,AB=AC,AD是△ABC的角平分线.若AB
=13,AD=12,则BC的长为( B )
A.5 B.10 C.20 D.24
B
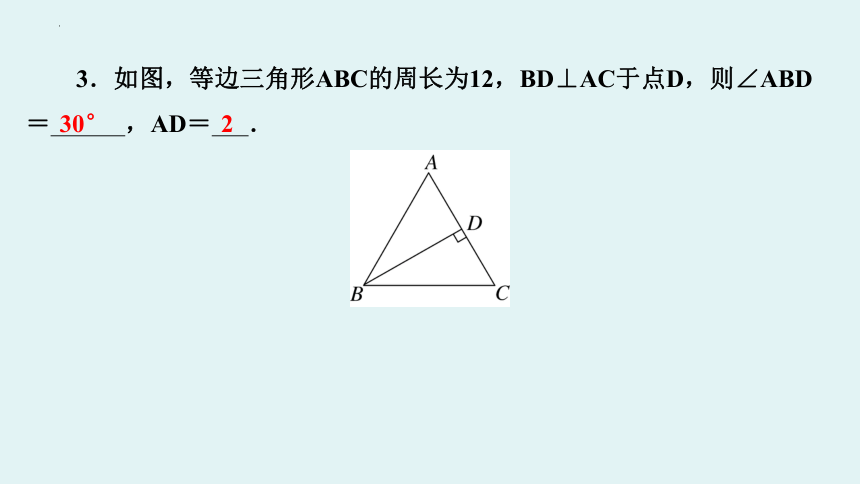
3.如图,等边三角形ABC的周长为12,BD⊥AC于点D,则∠ABD
= ,AD= .
30°
2
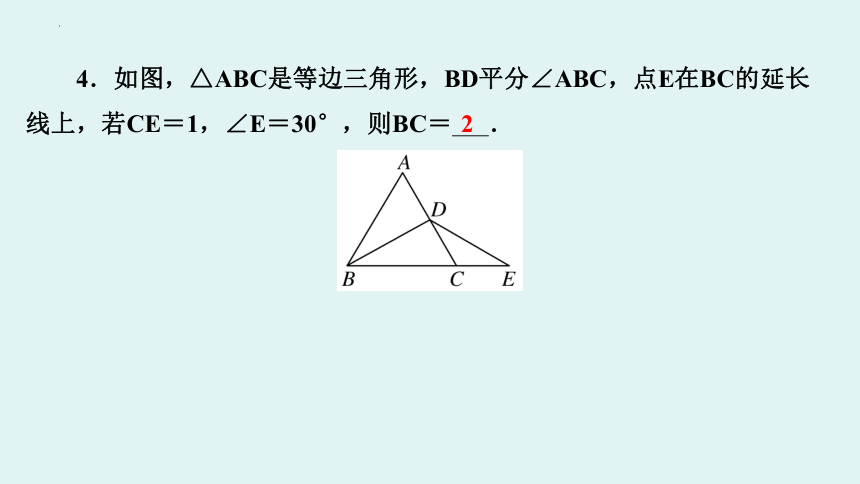
4.如图,△ABC是等边三角形,BD平分∠ABC,点E在BC的延长
线上,若CE=1,∠E=30°,则BC= .
2
5.如图,在△ABC中,点D,E分别是AB,AC边上的点,BD=CE,
∠ABE=∠ACD,BE与CD相交于点F.求证:△ABC是等腰三角形.
证明:在△BFD和△CFE中,
∴△BFD≌△CFE(AAS).∴FB=FC.
∴∠FBC=∠FCB.∴∠ABE+∠FBC=∠ACD+∠FCB.
∴∠ABC=∠ACB.∴AB=AC.
∴△ABC是等腰三角形.
直角三角形
6.下列条件,不能判定两个直角三角形全等的是( A )
A.两个锐角对应相等
B.斜边和一直角边分别对应相等
C.两条直角边分别对应相等
D.一条直角边相等且另一条直角边上的中线对应相等
A
7.在△ABC中,∠A=40°,要使△ABC为直角三角形,则∠B的
度数为 .
8.已知直角三角形的两边长为6和10,则斜边长为____________ .
50°或90°
10或2
9.如图,在△ABC中,AB=AC,△ABC的高BH,CM交于点P.
(1)求证:PB=PC;
(1)证明:∵AB=AC,
∴∠ABC=∠ACB.
∵BH,CM为△ABC的高,
∴∠BMC=∠CHB=90°.
∴∠ABC+∠BCM=90°,∠ACB+∠CBH=90°.
∴∠BCM=∠CBH.∴PB=PC.
(2)若PB=5,PH=3,求AB的长.
(2)解:∵PB=PC,PB=5,∴PC=5.
∵PH=3,∠CHB=90°,∴CH==4.
设AB=AC=x,则AH=x-4.
在Rt△ABH中,AH2+BH2=AB2,
∴(x-4)2+(5+3)2=x2.∴x=10,即AB=10.
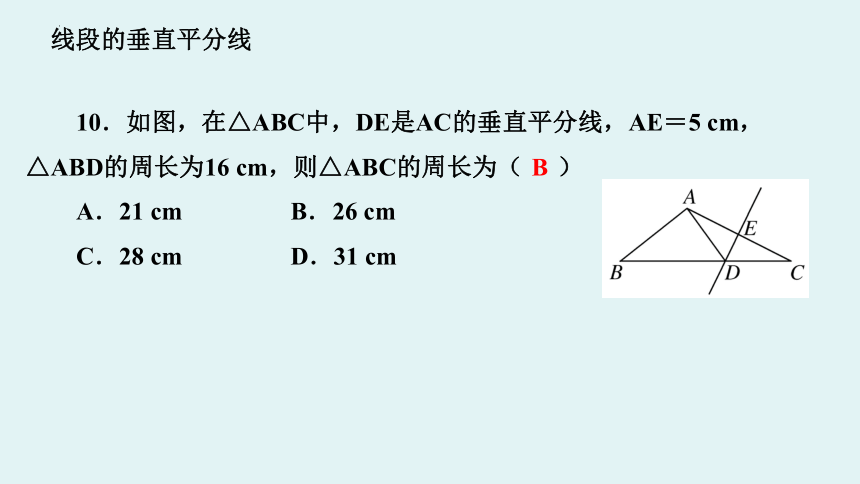
线段的垂直平分线
10.如图,在△ABC中,DE是AC的垂直平分线,AE=5 cm,
△ABD的周长为16 cm,则△ABC的周长为( B )
A.21 cm B.26 cm
C.28 cm D.31 cm
B
11.如图,在△ABC中,AB=AC,∠BAC=120°.
(1)作AC的垂直平分线EF交AC于点E,交BC于点F;
(2)若BC=6,求CF的长.
解:(1)如图所示.
(2)如图,连接AF.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=×(180°-120°)=30°.
∵EF垂直平分AC,∴AF=CF.∴∠FAC=∠C=30°.∴∠BAF=90°.
∴BF=2AF=2CF.∴3CF=BC=6.∴CF=2.
角平分线
12.如图,在△ABC中,∠C=90°,AD平分∠BAC,AB=8,CD
=3,则△ABD的面积为 .
12
13.如图,DE⊥AB于点E,DF⊥AC于点F,BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°.
∴△BDE和△CDF均为直角三角形.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).∴DE=DF.
又DE⊥AB,DF⊥AC,∴AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.
(2)解:AB+AC=2AE.理由如下:
在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF(HL).∴AE=AF.
∴AB+AC=(AE-BE)+(AF+CF)=AE-BE+AE+BE=2AE.
转化思想就是将未知问题转化成已知问题,将比较复杂的问题转化
成比较简单的问题的一种思想方法.
转化
14.如图,在Rt△ABC中,∠C=90°,∠B=30°,以顶点A为圆心,
适当长为半径画弧,分别交AC,AB于点E,F;再分别以点E,F为圆
心,大于EF的长为半径画弧,两弧交于点P,作射线AP交BC于点D,则
CD与BD的数量关系是__________________ .
CD=BD(或BD=2CD)
点拨:本题可利用角平分线的性质转化线段CD,或利用等腰三角形的
判定转化线段BD.
15.如图,△ABC是等边三角形,AB=6,点N是AB的中点,AD是BC
边上的中线,点M是AD上的一个动点,连接BM,MN,则BM+MN的最
小值是________ .
3
点拨:本题利用等边三角形的性质及轴对称中最短路径问题将两个线
段的和转化成求已知线段的长.
1.下列命题的逆命题不正确的是( D )
A.角平分线上的点到角两边的距离相等
B.两直线平行,内错角相等
C.等腰三角形的两个底角相等
D.对顶角相等
D
核心练习
2.如图,在△ABC中,AB=AC,用尺规作图的方法作出射线AD和
直线EF,AD交EF于点O,连接BE,OC.下列结论中,不一定成立的是
( A )
A.AE⊥BE
B.EF平分∠AEB
C.OA=OC
D.AB=BE+EC
A
3.如图,把等边三角形ABC沿DE折叠,使点A恰好落在BC边上的
点P处,且DP⊥BC于点P.若BP=4 cm,则EC=__________ cm.
(2+2)
4.将一副直角三角板按如图所示的位置摆放,使点A,B,D在同一
直线上,且EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=
60°,若DE=2 ,则BD= 3 .
3
5.如图,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;
②AD=AE;③BD=CE.以此三个等式中的两个作为条件,另一个作为结
论,构成三个命题:①② ③;①③ ②;②③ ①.
(1)以上三个命题是真命题的是 ;
(直接作答)
(2)请选择其中一个真命题,并证明.(先写出所选命题,然后证明)
解:选择①③ ②.
①② ③;①③ ②;②③ ①
证明:∵AB=AC,∴∠B=∠C.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).∴AD=AE.(答案不唯一)
6.如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的
中线,且BD=BE,CD的垂直平分线FM交AC于点F,交BC于点M,FM
=2.
(1)求∠ADE的度数.
解:(1)在△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=(180°-∠BAC)=30°.
∵BD=BE,∴∠BDE=∠BED=(180°-∠B)=75°.
在△ABC中,AB=AC,AD是BC边上的中线,
∴AD⊥BC,即∠ADB=90°.
∴∠ADE=∠ADB-∠BDE=15°.
(2)△ADF是等边三角形吗?为什么?
(2)△ADF是等边三角形.理由如下:
∵FM是CD的垂直平分线,∴DF=CF.
由(1)知∠C=30°.∴∠FDC=∠C=30°.
∴∠AFD=∠C+∠FDC=60°.
由(1)知AD⊥BC.∴∠ADC=90°.
∴∠DAF=90°-∠C=60°.
∴∠AFD=∠DAF=∠ADF=60°.
∴△ADF是等边三角形.
(3)求AB的长.
(3)∵FM是CD的垂直平分线,
∴∠FMC=90°,DF=CF.
由(1)知∠C=30°.∴DF=CF=2FM=4.
由(2)知△ADF是等边三角形.
∴AF=DF=4.∴AC=AF+CF=4+4=8.
∵AB=AC,∴AB=8.
解与等腰三角形有关问题时,考虑不全面
1.(1)已知实数x,y满足|x-5|+ =0,则以x,y的值为两边
长的等腰三角形的周长是 .
(2)已知等腰三角形的一个内角为50°,则它的顶角的度数为
.
【易错点拨】 题(1)未明确腰和底边,题(2)未明确底角和顶角,需要分
类讨论,切记求长度时还要结合三角形三边关系求解.
27
50°或
80°
易错点拨
未考虑三角形形状
2.等腰三角形一腰上的高与另一腰的夹角为30°,腰长为6,则其
底边上的高是________ .
3.在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所
得的锐角为50°,则∠B的度数为 .
【易错点拨】 此类题目条件中未给出图形,在画图分析解答时,容易只
考虑锐角三角形的情况,而忽略钝角三角形的情况.
3或3
70°或20°
未能正确判断直角边和斜边
4.在Rt△ABC中,BC=3,AB=4,则这个三角形的周长为
______ .
【易错点拨】 在没有明确直角边、斜边时,应分类讨论,以免漏解.本
题易误认为已知的两条边是直角边.
12或7
+
对角平分线的性质理解不准确
5.如图,点Q是△OAB的角平分线OP上的一点,PC⊥OA于点C,
PD⊥OB于点D,QE⊥OB于点E,FQ⊥OQ,交OA于点F,则下列结论
正确的是( B )
A.PA=PB B.PC=PD
C.PC=QE D.QE=QF
B
【易错点拨】 应用角平分线的性质时应注意两点:一是点在角平分线上;二是垂足在角的两边上.本题易误把FQ的长看成点Q到OA的距离.
1.已知等腰三角形的一个角为72°,则其底角为( D )
A.54° B.45°
C.60° D.72°或54°
D
复习训练
2.已知一个等腰三角形的两边长分别是2和5,则该等腰三角形的周
长为( B )
A.9 B.12 C.9或12 D.7
B
3.如图,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点
N,交AB于点M,BC=3 cm,则△BCN的周长为( D )
A.10 cm B.4 cm C.6 cm D.7 cm
D
4.如图,PE⊥OA于点E,PF⊥OB于点F,若PE=PF,∠AOB=
48°,则∠OPE= °.
66
5.如图,在△ABC中,∠A=90°,DE是BC的垂直平分线,AD=
DE,则∠C的度数是 °.
30
6.定理“如果直角三角形的两直角边分别是a,b,斜边是c,那么a2
+b2=c2”的逆定理是
.
如果三角形的三边长a,b,c满足a2+b2=c2,那
么这个三角形是直角三角形,且a,b是直角边,c是斜边
循环复习
7.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DE=
2,AC=3,则△ADC的面积为 .
3
1.如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD=
( B )
A.10 B.5 C.4 D.3
B
基础训练
2.如图,AP平分∠BAC,PB⊥AB,PC⊥AC,垂足分别为点B,
C,PB=3,AC=8,则四边形ABPC的面积为 24 .
24
3.如图,直线l1∥l2,AB=BC,CD⊥AB于点D,若∠DCA=
25°,则∠1的度数为 65° .
65°
4.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半
径作圆弧,两弧相交于点M和点N,作直线MN交CB于点D,连接AD.若
AC=8,BC=15,则△ACD的周长为 23 .
23
5.如图,在△ABC中,AB=4,点D为BC上一点,AD=BD=
4,在AD上找一点E,使BE=AC.
( 1 )判断△ABD的形状,并说明理由;
( 1 )解:△ABD是等腰直角三角形.理由如下:
在△ABD中,∵AD=BD=4,AB=4,
∴AD2+BD2=32=AB2.
∴△ABD为等腰直角三角形,∠ADB=90°.
( 2 )证明:由( 1 )知∠ADB=90°.
∵∠ADB+∠ADC=180°,
∴∠ADC=∠ADB=90°.
∴△BDE和△ADC为直角三角形.
在Rt△BDE和Rt△ADC中,
∴Rt△BDE≌Rt△ADC( HL ).
( 2 )求证:△BDE≌△ADC.
6.如图,△ABC的顶点B,C的坐标分别是( 1,0 ),( 0, ),且
∠ABC=90°,∠A=30°,则顶点A的坐标是 ( 4,) .
( 4,)
7.如图,在△ABC中,∠BAC=120°,分别作AC,AB两边的垂
直平分线PM,PN,垂足分别是点M,N,给出以下说法:①∠P=
60°;②∠EAF=∠B+∠C;③PE=PF;④点P到点B和点C的距离相
等.其中正确的是 ①②④ .( 填序号 )
①②④
8.如图,将一张长方形纸片ABCD沿EF折叠,使C,A两点重合,
点D落在点G处.已知AB=4,BC=8.
( 1 )求证:△AEF是等腰三角形;
( 1 )证明:由折叠的性质,可知∠AEF=∠CEF.
由长方形的性质,得AD∥BC.∴∠AFE=∠CEF.
∴∠AEF=∠AFE.∴AE=AF.
∴△AEF是等腰三角形.
( 2 )求线段FD的长.
( 2 )解:由折叠的性质,得AE=CE.
设CE=x,则AE=x,BE=BC-CE=8-x.
∵∠B=90°,
∴在Rt△ABE中,AB2+BE2=AE2,
即42+( 8-x )2=x2.解得x=5,即AE=5.
由( 1 ),得AE=AF.∴AF=5.
∴FD=AD-AF=BC-AF=8-5=3.
第一章 三角形的证明
第11课 三角形的证明章末复习
数学(RS版) 八年级下册
60°
等腰
互余
互余
相等
相等
思维导图
等腰三角形
1.如图,在△ABC中,AB=AC.
(1)若∠A=50°,则∠C= ;
(2)若∠B=50°,则∠A= .
65°
80°
高频考点
2.如图,在△ABC中,AB=AC,AD是△ABC的角平分线.若AB
=13,AD=12,则BC的长为( B )
A.5 B.10 C.20 D.24
B
3.如图,等边三角形ABC的周长为12,BD⊥AC于点D,则∠ABD
= ,AD= .
30°
2
4.如图,△ABC是等边三角形,BD平分∠ABC,点E在BC的延长
线上,若CE=1,∠E=30°,则BC= .
2
5.如图,在△ABC中,点D,E分别是AB,AC边上的点,BD=CE,
∠ABE=∠ACD,BE与CD相交于点F.求证:△ABC是等腰三角形.
证明:在△BFD和△CFE中,
∴△BFD≌△CFE(AAS).∴FB=FC.
∴∠FBC=∠FCB.∴∠ABE+∠FBC=∠ACD+∠FCB.
∴∠ABC=∠ACB.∴AB=AC.
∴△ABC是等腰三角形.
直角三角形
6.下列条件,不能判定两个直角三角形全等的是( A )
A.两个锐角对应相等
B.斜边和一直角边分别对应相等
C.两条直角边分别对应相等
D.一条直角边相等且另一条直角边上的中线对应相等
A
7.在△ABC中,∠A=40°,要使△ABC为直角三角形,则∠B的
度数为 .
8.已知直角三角形的两边长为6和10,则斜边长为____________ .
50°或90°
10或2
9.如图,在△ABC中,AB=AC,△ABC的高BH,CM交于点P.
(1)求证:PB=PC;
(1)证明:∵AB=AC,
∴∠ABC=∠ACB.
∵BH,CM为△ABC的高,
∴∠BMC=∠CHB=90°.
∴∠ABC+∠BCM=90°,∠ACB+∠CBH=90°.
∴∠BCM=∠CBH.∴PB=PC.
(2)若PB=5,PH=3,求AB的长.
(2)解:∵PB=PC,PB=5,∴PC=5.
∵PH=3,∠CHB=90°,∴CH==4.
设AB=AC=x,则AH=x-4.
在Rt△ABH中,AH2+BH2=AB2,
∴(x-4)2+(5+3)2=x2.∴x=10,即AB=10.
线段的垂直平分线
10.如图,在△ABC中,DE是AC的垂直平分线,AE=5 cm,
△ABD的周长为16 cm,则△ABC的周长为( B )
A.21 cm B.26 cm
C.28 cm D.31 cm
B
11.如图,在△ABC中,AB=AC,∠BAC=120°.
(1)作AC的垂直平分线EF交AC于点E,交BC于点F;
(2)若BC=6,求CF的长.
解:(1)如图所示.
(2)如图,连接AF.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=×(180°-120°)=30°.
∵EF垂直平分AC,∴AF=CF.∴∠FAC=∠C=30°.∴∠BAF=90°.
∴BF=2AF=2CF.∴3CF=BC=6.∴CF=2.
角平分线
12.如图,在△ABC中,∠C=90°,AD平分∠BAC,AB=8,CD
=3,则△ABD的面积为 .
12
13.如图,DE⊥AB于点E,DF⊥AC于点F,BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°.
∴△BDE和△CDF均为直角三角形.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).∴DE=DF.
又DE⊥AB,DF⊥AC,∴AD平分∠BAC.
(2)写出AB+AC与AE之间的等量关系,并说明理由.
(2)解:AB+AC=2AE.理由如下:
在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF(HL).∴AE=AF.
∴AB+AC=(AE-BE)+(AF+CF)=AE-BE+AE+BE=2AE.
转化思想就是将未知问题转化成已知问题,将比较复杂的问题转化
成比较简单的问题的一种思想方法.
转化
14.如图,在Rt△ABC中,∠C=90°,∠B=30°,以顶点A为圆心,
适当长为半径画弧,分别交AC,AB于点E,F;再分别以点E,F为圆
心,大于EF的长为半径画弧,两弧交于点P,作射线AP交BC于点D,则
CD与BD的数量关系是__________________ .
CD=BD(或BD=2CD)
点拨:本题可利用角平分线的性质转化线段CD,或利用等腰三角形的
判定转化线段BD.
15.如图,△ABC是等边三角形,AB=6,点N是AB的中点,AD是BC
边上的中线,点M是AD上的一个动点,连接BM,MN,则BM+MN的最
小值是________ .
3
点拨:本题利用等边三角形的性质及轴对称中最短路径问题将两个线
段的和转化成求已知线段的长.
1.下列命题的逆命题不正确的是( D )
A.角平分线上的点到角两边的距离相等
B.两直线平行,内错角相等
C.等腰三角形的两个底角相等
D.对顶角相等
D
核心练习
2.如图,在△ABC中,AB=AC,用尺规作图的方法作出射线AD和
直线EF,AD交EF于点O,连接BE,OC.下列结论中,不一定成立的是
( A )
A.AE⊥BE
B.EF平分∠AEB
C.OA=OC
D.AB=BE+EC
A
3.如图,把等边三角形ABC沿DE折叠,使点A恰好落在BC边上的
点P处,且DP⊥BC于点P.若BP=4 cm,则EC=__________ cm.
(2+2)
4.将一副直角三角板按如图所示的位置摆放,使点A,B,D在同一
直线上,且EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=
60°,若DE=2 ,则BD= 3 .
3
5.如图,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;
②AD=AE;③BD=CE.以此三个等式中的两个作为条件,另一个作为结
论,构成三个命题:①② ③;①③ ②;②③ ①.
(1)以上三个命题是真命题的是 ;
(直接作答)
(2)请选择其中一个真命题,并证明.(先写出所选命题,然后证明)
解:选择①③ ②.
①② ③;①③ ②;②③ ①
证明:∵AB=AC,∴∠B=∠C.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).∴AD=AE.(答案不唯一)
6.如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的
中线,且BD=BE,CD的垂直平分线FM交AC于点F,交BC于点M,FM
=2.
(1)求∠ADE的度数.
解:(1)在△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=(180°-∠BAC)=30°.
∵BD=BE,∴∠BDE=∠BED=(180°-∠B)=75°.
在△ABC中,AB=AC,AD是BC边上的中线,
∴AD⊥BC,即∠ADB=90°.
∴∠ADE=∠ADB-∠BDE=15°.
(2)△ADF是等边三角形吗?为什么?
(2)△ADF是等边三角形.理由如下:
∵FM是CD的垂直平分线,∴DF=CF.
由(1)知∠C=30°.∴∠FDC=∠C=30°.
∴∠AFD=∠C+∠FDC=60°.
由(1)知AD⊥BC.∴∠ADC=90°.
∴∠DAF=90°-∠C=60°.
∴∠AFD=∠DAF=∠ADF=60°.
∴△ADF是等边三角形.
(3)求AB的长.
(3)∵FM是CD的垂直平分线,
∴∠FMC=90°,DF=CF.
由(1)知∠C=30°.∴DF=CF=2FM=4.
由(2)知△ADF是等边三角形.
∴AF=DF=4.∴AC=AF+CF=4+4=8.
∵AB=AC,∴AB=8.
解与等腰三角形有关问题时,考虑不全面
1.(1)已知实数x,y满足|x-5|+ =0,则以x,y的值为两边
长的等腰三角形的周长是 .
(2)已知等腰三角形的一个内角为50°,则它的顶角的度数为
.
【易错点拨】 题(1)未明确腰和底边,题(2)未明确底角和顶角,需要分
类讨论,切记求长度时还要结合三角形三边关系求解.
27
50°或
80°
易错点拨
未考虑三角形形状
2.等腰三角形一腰上的高与另一腰的夹角为30°,腰长为6,则其
底边上的高是________ .
3.在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所
得的锐角为50°,则∠B的度数为 .
【易错点拨】 此类题目条件中未给出图形,在画图分析解答时,容易只
考虑锐角三角形的情况,而忽略钝角三角形的情况.
3或3
70°或20°
未能正确判断直角边和斜边
4.在Rt△ABC中,BC=3,AB=4,则这个三角形的周长为
______ .
【易错点拨】 在没有明确直角边、斜边时,应分类讨论,以免漏解.本
题易误认为已知的两条边是直角边.
12或7
+
对角平分线的性质理解不准确
5.如图,点Q是△OAB的角平分线OP上的一点,PC⊥OA于点C,
PD⊥OB于点D,QE⊥OB于点E,FQ⊥OQ,交OA于点F,则下列结论
正确的是( B )
A.PA=PB B.PC=PD
C.PC=QE D.QE=QF
B
【易错点拨】 应用角平分线的性质时应注意两点:一是点在角平分线上;二是垂足在角的两边上.本题易误把FQ的长看成点Q到OA的距离.
1.已知等腰三角形的一个角为72°,则其底角为( D )
A.54° B.45°
C.60° D.72°或54°
D
复习训练
2.已知一个等腰三角形的两边长分别是2和5,则该等腰三角形的周
长为( B )
A.9 B.12 C.9或12 D.7
B
3.如图,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点
N,交AB于点M,BC=3 cm,则△BCN的周长为( D )
A.10 cm B.4 cm C.6 cm D.7 cm
D
4.如图,PE⊥OA于点E,PF⊥OB于点F,若PE=PF,∠AOB=
48°,则∠OPE= °.
66
5.如图,在△ABC中,∠A=90°,DE是BC的垂直平分线,AD=
DE,则∠C的度数是 °.
30
6.定理“如果直角三角形的两直角边分别是a,b,斜边是c,那么a2
+b2=c2”的逆定理是
.
如果三角形的三边长a,b,c满足a2+b2=c2,那
么这个三角形是直角三角形,且a,b是直角边,c是斜边
循环复习
7.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DE=
2,AC=3,则△ADC的面积为 .
3
1.如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD=
( B )
A.10 B.5 C.4 D.3
B
基础训练
2.如图,AP平分∠BAC,PB⊥AB,PC⊥AC,垂足分别为点B,
C,PB=3,AC=8,则四边形ABPC的面积为 24 .
24
3.如图,直线l1∥l2,AB=BC,CD⊥AB于点D,若∠DCA=
25°,则∠1的度数为 65° .
65°
4.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半
径作圆弧,两弧相交于点M和点N,作直线MN交CB于点D,连接AD.若
AC=8,BC=15,则△ACD的周长为 23 .
23
5.如图,在△ABC中,AB=4,点D为BC上一点,AD=BD=
4,在AD上找一点E,使BE=AC.
( 1 )判断△ABD的形状,并说明理由;
( 1 )解:△ABD是等腰直角三角形.理由如下:
在△ABD中,∵AD=BD=4,AB=4,
∴AD2+BD2=32=AB2.
∴△ABD为等腰直角三角形,∠ADB=90°.
( 2 )证明:由( 1 )知∠ADB=90°.
∵∠ADB+∠ADC=180°,
∴∠ADC=∠ADB=90°.
∴△BDE和△ADC为直角三角形.
在Rt△BDE和Rt△ADC中,
∴Rt△BDE≌Rt△ADC( HL ).
( 2 )求证:△BDE≌△ADC.
6.如图,△ABC的顶点B,C的坐标分别是( 1,0 ),( 0, ),且
∠ABC=90°,∠A=30°,则顶点A的坐标是 ( 4,) .
( 4,)
7.如图,在△ABC中,∠BAC=120°,分别作AC,AB两边的垂
直平分线PM,PN,垂足分别是点M,N,给出以下说法:①∠P=
60°;②∠EAF=∠B+∠C;③PE=PF;④点P到点B和点C的距离相
等.其中正确的是 ①②④ .( 填序号 )
①②④
8.如图,将一张长方形纸片ABCD沿EF折叠,使C,A两点重合,
点D落在点G处.已知AB=4,BC=8.
( 1 )求证:△AEF是等腰三角形;
( 1 )证明:由折叠的性质,可知∠AEF=∠CEF.
由长方形的性质,得AD∥BC.∴∠AFE=∠CEF.
∴∠AEF=∠AFE.∴AE=AF.
∴△AEF是等腰三角形.
( 2 )求线段FD的长.
( 2 )解:由折叠的性质,得AE=CE.
设CE=x,则AE=x,BE=BC-CE=8-x.
∵∠B=90°,
∴在Rt△ABE中,AB2+BE2=AE2,
即42+( 8-x )2=x2.解得x=5,即AE=5.
由( 1 ),得AE=AF.∴AF=5.
∴FD=AD-AF=BC-AF=8-5=3.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
