北师大版(2012)数学八年级上册 第四章 一次函数 期末章节拔高练习(含答案)
文档属性
| 名称 | 北师大版(2012)数学八年级上册 第四章 一次函数 期末章节拔高练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 319.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 20:25:48 | ||
图片预览

文档简介
北师大版(2012)数学八年级上册第四章一次函数期末章节拔高练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,已知两车相遇时快车比慢车多行驶40千米,快车到达乙地时,慢车还有( )千米到达甲地.
A.70 B.80 C.90 D.100
2.一次函数,y随着x的增大而减小,且,则该函数的图像不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限.
3.已知长方体的高是1,长和宽分别是、,体积是,则下列说法正确的是( )
A.是的正比例函数 B.是的正比例函数
C.是或的正比例函数 D.是的正比例函数
4.若点在一次函数的图象上,则的值( )
A. B.3 C. D.2
5.下列各点中,在直线y=2x上的点是( )
A.(1,1) B.(2,1) C.(2,-2) D.(1,2)
6.在函数中,自变量的取值范围是( )
A. B. C. D.
7.已知一次函数y=kx+1的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )
A.(﹣2,0) B.(2,﹣1) C.(1,1) D.(3,2)
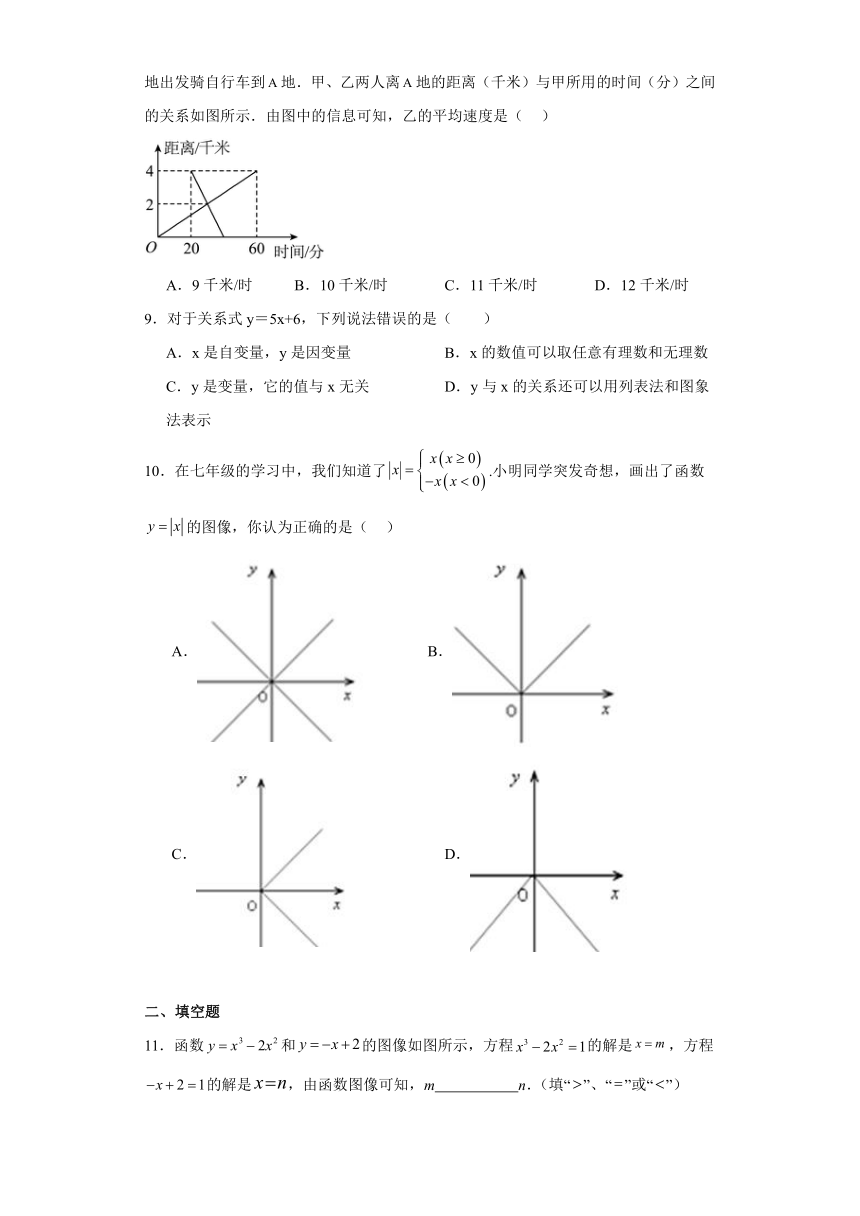
8.已知,两地相距4千米.上午8:00,甲从地出发步行到地,8:20乙从地出发骑自行车到地.甲、乙两人离地的距离(千米)与甲所用的时间(分)之间的关系如图所示.由图中的信息可知,乙的平均速度是( )
A.9千米/时 B.10千米/时 C.11千米/时 D.12千米/时
9.对于关系式y=5x+6,下列说法错误的是( )
A.x是自变量,y是因变量 B.x的数值可以取任意有理数和无理数
C.y是变量,它的值与x无关 D.y与x的关系还可以用列表法和图象法表示
10.在七年级的学习中,我们知道了.小明同学突发奇想,画出了函数的图像,你认为正确的是( )
A. B.
C. D.
二、填空题
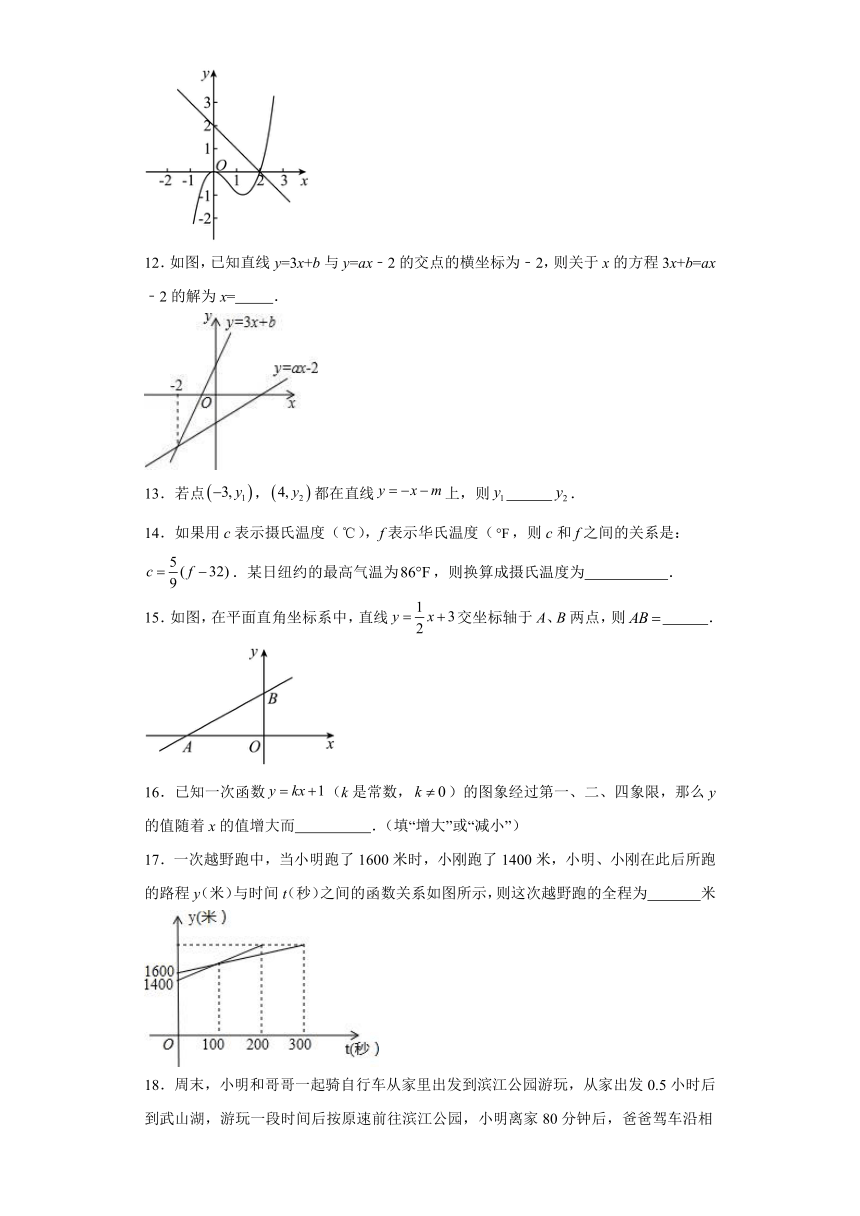
11.函数和的图像如图所示,方程的解是,方程的解是,由函数图像可知,m n.(填“”、“”或“”)
12.如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,则关于x的方程3x+b=ax﹣2的解为x= .
13.若点,都在直线上,则 .
14.如果用c表示摄氏温度(),f表示华氏温度(,则c和f之间的关系是:.某日纽约的最高气温为,则换算成摄氏温度为 .
15.如图,在平面直角坐标系中,直线交坐标轴于A、B两点,则 .
16.已知一次函数(k是常数,)的图象经过第一、二、四象限,那么y的值随着x的值增大而 .(填“增大”或“减小”)
17.一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为 米
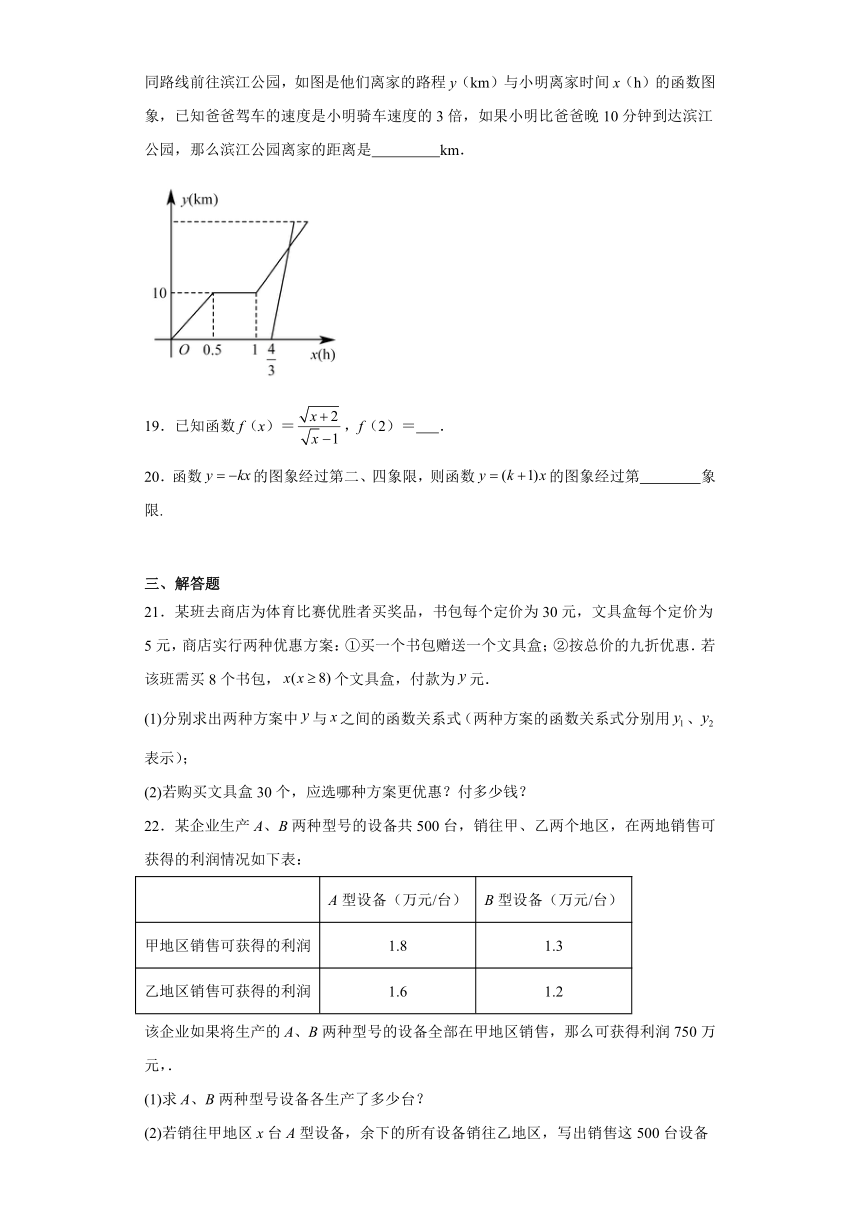
18.周末,小明和哥哥一起骑自行车从家里出发到滨江公园游玩,从家出发0.5小时后到武山湖,游玩一段时间后按原速前往滨江公园,小明离家80分钟后,爸爸驾车沿相同路线前往滨江公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知爸爸驾车的速度是小明骑车速度的3倍,如果小明比爸爸晚10分钟到达滨江公园,那么滨江公园离家的距离是 km.
19.已知函数f(x)=,f(2)= .
20.函数的图象经过第二、四象限,则函数的图象经过第 象限.
三、解答题
21.某班去商店为体育比赛优胜者买奖品,书包每个定价为30元,文具盒每个定价为5元,商店实行两种优惠方案:①买一个书包赠送一个文具盒;②按总价的九折优惠.若该班需买8个书包,个文具盒,付款为元.
(1)分别求出两种方案中与之间的函数关系式(两种方案的函数关系式分别用、表示);
(2)若购买文具盒30个,应选哪种方案更优惠?付多少钱?
22.某企业生产A、B两种型号的设备共500台,销往甲、乙两个地区,在两地销售可获得的利润情况如下表:
A型设备(万元/台) B型设备(万元/台)
甲地区销售可获得的利润 1.8 1.3
乙地区销售可获得的利润 1.6 1.2
该企业如果将生产的A、B两种型号的设备全部在甲地区销售,那么可获得利润750万元,.
(1)求A、B两种型号设备各生产了多少台?
(2)若销往甲地区x台A型设备,余下的所有设备销往乙地区,写出销售这500台设备可获得的利润y(万元)与x之间的函数表达式,并求利润的最大值.
23.为了响应政府“绿色出行”的号召,李华选择骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图像回答下列问题.
(1)李华到达离家最远的地方是几时?此时离家多远?
(2)李华返回时的速度是多少?
(3)李华全程骑车的平均速度是多少?
24.小林同学在保养自己的山地自行车时发现,自行车每节链条的长度为,交叉重叠部分的圆的直径为.
(1)观察图形填表:
链条节数(节) 2 3 6
链条长度() ________ ________ ________
(2)如果节链条的总长度是,求与之间的关系式.
25.甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元,如果一次购买以上的苹果,超过的部分按标价6折售卖.(单位:)表示购买苹果的重量,(单位:元)表示付款金额.
(1)文文购买苹果需付款___________元,购买苹果需付款____________元;
(2)求付款金额关于购买苹果的重量的函数解析式;
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元,且全部按标价的8折售卖.文文如果要购买苹果,请问她在哪个超市购买更划算?
26.电力公司为鼓励市民节约用电,采取按月用电量分段收费办法若某户民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1)分别写出当和时,y与x的函数关系式:
(2)利用函数关系式,说明电力公司采取的收费标准;
(3)若该用户某月用电52度,则应缴费多少元?若该用户某月缴费105元时,则该用户该几用了多少度电?
27.某游泳馆夏季推出两种游泳付费方式.方式一:先购买会员证,每张会员证200元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费15元.
设小强计划今年夏季游泳次数为x(x为正整数).
(1)根据题意,填写下表:
游泳次数 10 15 …
方式一的总费用(元) 250 …
方式二的总费用(元) 150 …
(2)设小强今年夏季游泳用方式一付费元,用方式二付费元,分别写出关于x的函数关系式;
(3)①若小强今年夏季用方式一和用方式二游泳的次数相同,且费用相同,则小强游泳的次数为_________次;
②若小强用同一种付费方式游泳30次,则他用方式一和用方式二中的方式__________付费方式,花费少;
③若小强用同一种付费方式游泳花费270元,则用方式一和用方式二中的方式_________付费方式,游泳的次数多.
参考答案:
1.A
2.A
3.D
4.B
5.D
6.A
7.B
8.D
9.C
10.B
11.
12.﹣2
13.
14.
15.
16.减小
17.2200
18.30
19./
20.一、三
21.(1);;
(2)方案①更省钱,付款350元.
22.(1)型号设备生产了200台,型号设备生产了300台;
(2),720万元.
23.(1)(1)李华到达离家最远的地方是在12时,此时离家30千米;(2)李华返回的途中速度为:千米/小时;(3)李华全程骑车的平均速度为:千米/小时.
24.(1)4.2;5.9;11
(2)
25.(1)30,46;(2)当时,,当时,;(3)甲超市
26.(1)当0≤x≤100时,y=0.65x,当x>100时,y=0.8x-15;
(2)月用电量在0度到100度之间时,每度电的收费的标准是0.65元;月用电量超出100度时,超过部分每度电的收费标准是0.8元;
(3)该用户某月用电52度,则应缴费33.8元,该用户某月缴费105元时,该用户该月用了150度电.
27.(1)275,225;(2),;(3)①20,②一,③二
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,已知两车相遇时快车比慢车多行驶40千米,快车到达乙地时,慢车还有( )千米到达甲地.
A.70 B.80 C.90 D.100
2.一次函数,y随着x的增大而减小,且,则该函数的图像不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限.
3.已知长方体的高是1,长和宽分别是、,体积是,则下列说法正确的是( )
A.是的正比例函数 B.是的正比例函数
C.是或的正比例函数 D.是的正比例函数
4.若点在一次函数的图象上,则的值( )
A. B.3 C. D.2
5.下列各点中,在直线y=2x上的点是( )
A.(1,1) B.(2,1) C.(2,-2) D.(1,2)
6.在函数中,自变量的取值范围是( )
A. B. C. D.
7.已知一次函数y=kx+1的图象经过点A,且y随x的增大而减小,则点A的坐标可以是( )
A.(﹣2,0) B.(2,﹣1) C.(1,1) D.(3,2)
8.已知,两地相距4千米.上午8:00,甲从地出发步行到地,8:20乙从地出发骑自行车到地.甲、乙两人离地的距离(千米)与甲所用的时间(分)之间的关系如图所示.由图中的信息可知,乙的平均速度是( )
A.9千米/时 B.10千米/时 C.11千米/时 D.12千米/时
9.对于关系式y=5x+6,下列说法错误的是( )
A.x是自变量,y是因变量 B.x的数值可以取任意有理数和无理数
C.y是变量,它的值与x无关 D.y与x的关系还可以用列表法和图象法表示
10.在七年级的学习中,我们知道了.小明同学突发奇想,画出了函数的图像,你认为正确的是( )
A. B.
C. D.
二、填空题
11.函数和的图像如图所示,方程的解是,方程的解是,由函数图像可知,m n.(填“”、“”或“”)
12.如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,则关于x的方程3x+b=ax﹣2的解为x= .
13.若点,都在直线上,则 .
14.如果用c表示摄氏温度(),f表示华氏温度(,则c和f之间的关系是:.某日纽约的最高气温为,则换算成摄氏温度为 .
15.如图,在平面直角坐标系中,直线交坐标轴于A、B两点,则 .
16.已知一次函数(k是常数,)的图象经过第一、二、四象限,那么y的值随着x的值增大而 .(填“增大”或“减小”)
17.一次越野跑中,当小明跑了1600米时,小刚跑了1400米,小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示,则这次越野跑的全程为 米
18.周末,小明和哥哥一起骑自行车从家里出发到滨江公园游玩,从家出发0.5小时后到武山湖,游玩一段时间后按原速前往滨江公园,小明离家80分钟后,爸爸驾车沿相同路线前往滨江公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象,已知爸爸驾车的速度是小明骑车速度的3倍,如果小明比爸爸晚10分钟到达滨江公园,那么滨江公园离家的距离是 km.
19.已知函数f(x)=,f(2)= .
20.函数的图象经过第二、四象限,则函数的图象经过第 象限.
三、解答题
21.某班去商店为体育比赛优胜者买奖品,书包每个定价为30元,文具盒每个定价为5元,商店实行两种优惠方案:①买一个书包赠送一个文具盒;②按总价的九折优惠.若该班需买8个书包,个文具盒,付款为元.
(1)分别求出两种方案中与之间的函数关系式(两种方案的函数关系式分别用、表示);
(2)若购买文具盒30个,应选哪种方案更优惠?付多少钱?
22.某企业生产A、B两种型号的设备共500台,销往甲、乙两个地区,在两地销售可获得的利润情况如下表:
A型设备(万元/台) B型设备(万元/台)
甲地区销售可获得的利润 1.8 1.3
乙地区销售可获得的利润 1.6 1.2
该企业如果将生产的A、B两种型号的设备全部在甲地区销售,那么可获得利润750万元,.
(1)求A、B两种型号设备各生产了多少台?
(2)若销往甲地区x台A型设备,余下的所有设备销往乙地区,写出销售这500台设备可获得的利润y(万元)与x之间的函数表达式,并求利润的最大值.
23.为了响应政府“绿色出行”的号召,李华选择骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图像回答下列问题.
(1)李华到达离家最远的地方是几时?此时离家多远?
(2)李华返回时的速度是多少?
(3)李华全程骑车的平均速度是多少?
24.小林同学在保养自己的山地自行车时发现,自行车每节链条的长度为,交叉重叠部分的圆的直径为.
(1)观察图形填表:
链条节数(节) 2 3 6
链条长度() ________ ________ ________
(2)如果节链条的总长度是,求与之间的关系式.
25.甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元,如果一次购买以上的苹果,超过的部分按标价6折售卖.(单位:)表示购买苹果的重量,(单位:元)表示付款金额.
(1)文文购买苹果需付款___________元,购买苹果需付款____________元;
(2)求付款金额关于购买苹果的重量的函数解析式;
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元,且全部按标价的8折售卖.文文如果要购买苹果,请问她在哪个超市购买更划算?
26.电力公司为鼓励市民节约用电,采取按月用电量分段收费办法若某户民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1)分别写出当和时,y与x的函数关系式:
(2)利用函数关系式,说明电力公司采取的收费标准;
(3)若该用户某月用电52度,则应缴费多少元?若该用户某月缴费105元时,则该用户该几用了多少度电?
27.某游泳馆夏季推出两种游泳付费方式.方式一:先购买会员证,每张会员证200元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费15元.
设小强计划今年夏季游泳次数为x(x为正整数).
(1)根据题意,填写下表:
游泳次数 10 15 …
方式一的总费用(元) 250 …
方式二的总费用(元) 150 …
(2)设小强今年夏季游泳用方式一付费元,用方式二付费元,分别写出关于x的函数关系式;
(3)①若小强今年夏季用方式一和用方式二游泳的次数相同,且费用相同,则小强游泳的次数为_________次;
②若小强用同一种付费方式游泳30次,则他用方式一和用方式二中的方式__________付费方式,花费少;
③若小强用同一种付费方式游泳花费270元,则用方式一和用方式二中的方式_________付费方式,游泳的次数多.
参考答案:
1.A
2.A
3.D
4.B
5.D
6.A
7.B
8.D
9.C
10.B
11.
12.﹣2
13.
14.
15.
16.减小
17.2200
18.30
19./
20.一、三
21.(1);;
(2)方案①更省钱,付款350元.
22.(1)型号设备生产了200台,型号设备生产了300台;
(2),720万元.
23.(1)(1)李华到达离家最远的地方是在12时,此时离家30千米;(2)李华返回的途中速度为:千米/小时;(3)李华全程骑车的平均速度为:千米/小时.
24.(1)4.2;5.9;11
(2)
25.(1)30,46;(2)当时,,当时,;(3)甲超市
26.(1)当0≤x≤100时,y=0.65x,当x>100时,y=0.8x-15;
(2)月用电量在0度到100度之间时,每度电的收费的标准是0.65元;月用电量超出100度时,超过部分每度电的收费标准是0.8元;
(3)该用户某月用电52度,则应缴费33.8元,该用户某月缴费105元时,该用户该月用了150度电.
27.(1)275,225;(2),;(3)①20,②一,③二
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
