对多解题、创新作图题和二次函数本质的考查三类题型的探究
文档属性
| 名称 | 对多解题、创新作图题和二次函数本质的考查三类题型的探究 |

|
|
| 格式 | zip | ||
| 文件大小 | 167.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-30 21:26:12 | ||
图片预览




文档简介
对多解题、创新作图题和二次函数本质的考查三类题型的探究
根据近年江西省试题特点,为了加强对多解题 ( http: / / www.21cnjy.com )、创新作图题和二次函数本质的考查题型的复习,有必要对此三类题型进行解读,以下对三类题型的一般类型及其解法进行例析.
一、满足条件的多解题:
满足条件的多解型试题不但知识覆盖面广,综合 ( http: / / www.21cnjy.com )性较强,题意构思精巧,而且在解答时需要灵活运用一种重要的数学思想方法——分类讨论,因此,这种题型今年不但在综合题中会有所涉及(往年常会出现),而且还规定把原来的多项选择型的第16题调整为一道“满足条件的多解”型题,对于这一调整笔者认为是进一步强调分类讨论这一思想方法考查,明确要求在复习中应加强对学生的多向思维的培养.同时也是为优化思维品质,克服思维的片面性,提高学生解题能力而出台一项具体措施.再则这类题的思维空间较大,解题时常出现考虑不全或不严谨,导致漏解、错解,因此我们应该熟练掌握这一题型的特征与解法.
1.在非负数问题中,是正是负没有明确时,分情况讨论而产生多解
例1. 已知a、b为实数,且ab≠0,那么= .
评析:本例是一道典型的分类讨论题.解答时首先根据公式“”把原式化为:,由于ab≠0即a、b都不为0,但a、b中哪个是正,哪个是负呢?所以只能分:①都是正;②都是负;③a为负,b为正;④a为正,b为负这四种情况来分别求值.
答案:0、2或-2
2.在一列数中,已知数与未知数没有明确大小时,分情况讨论而产生多解
例2.小明等五名同学四月份参加某次数学测验 ( http: / / www.21cnjy.com )(满分为120)的成绩如下:100、100、x、x、80.已知这组数据的中位数和平均数相等,那么整数x的值为 .
评析:由于一列数的中位数是 ( http: / / www.21cnjy.com )先按大小顺序排列后,最中间的那个数或最中间那两个数的平均值;题中x的大小有三种可能:①120≥x>100,②80<x≤100,③0≤x≤80,结合中位数、平均数的定义,可获得整数x值.本例抓住了x相对100和80大小可能性来分类,这种分类只要不漏掉某种情况,应该是不会出错的.
答案: 110或60(有一个非整数值已舍去)
3.在实际问题中,某方面的情境不明确时,分情况讨论而产生多解
例3.“五一”期间,某超市推出如下购物优惠方案:
一次性购物在100元(不含100元)以内时,不享受优惠;
(2)一次性购物在100元(含100元)以上,300元(不含300元)以内时一律享受九折的优惠;
(3)一次购物在300元(含300元)以上时,一律享受八折的优惠.
在此期间某顾客一次性购物付款252元,那么该顾客比平时购买总价相同的商品(没有优惠的时候)优惠了 元.
评析:题中情境有一个不明确的地方,即是:顾客优惠后的付款是252元,那么他所购买的商品的实际价格是在300元以下,还是多于300元呢?于是我们应分两种情况讨论.若是享受了优惠方案(2),则商品实价为=280元;若是享受了优惠方案(3),则商品实价为=315元.
像本例一样的问题,分类时,一定要按可能出现的情境来分类,否则会出现漏解现象,或者陷于无法入手的情形.
答案: 28或63.
4..在等腰三角形问题中,腰和底没有明确时,分情况讨论而产生多解
例4.已知,如图1:在平面直角坐标系中 ( http: / / www.21cnjy.com ),O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .
评析:题目给出了条件“△ODP是等腰三角形”,但未指明在△ODP中哪两条边相等,从而需要分情况考虑.但这里分类方法有几种:
如:方法1:OD、DP、OP轮流为底边,同时要注意以OD为底边时OP、PD是腰,但不会等于5,易产生错解,以OP为底边时又易漏掉一种情况.
方法2:∠POD、∠ODP、∠OP ( http: / / www.21cnjy.com )D轮流为顶角,这样分类同时还要考虑顶角可以是锐角、直角、钝角.本题由于腰为5的限制,故直角是不可能,∠POD为钝角不可能,∠PDO既可以是锐角,又可以为钝角.
方法3:由于腰为5,矩形的宽为4, ( http: / / www.21cnjy.com )易联想到勾3、股4、弦5,所以在OA上,在O点的右边取一点E,使OE=3,则OP=OD=5,在D点的左边取一点F,使DF=3,则OF=2,DP=OD=5,在D点的右边取一点G,使DG=3,则OG=8,DP=OD=5,这样P点坐标可直接写出.
这道题告诉我们,在抓住了分类讨论的特 ( http: / / www.21cnjy.com )征后,还要学会掌握分类的标准(或说方法).而有了分类的标准,就要自始至终使用这一标准分类,同时在求满足条件的点的坐标时,画出相应的图形,使用图形分析求解也是十分必要的,还有一点值得强调的是,分类后还应注意题中约束条件,谨防出现不合要求的解或漏解现象.
答案:(3,4),(2,4),(8,4).
5.在直角三角形问题中.直角边和斜边没有明确时,分情况讨论而产生多解
例5.线段AB的两端点的坐标为A(-1,0),B(0,-2)现请你在坐标轴上找一点P,
使得以P、A、B为顶点的三角形是直角三角形,则满足条件的P点的坐标是
评析:本例思考方法类似于例4,分类的标准也有几种,其中
可以分别以AB、AP、BP为斜边来确定P点的坐标.
答案:如图所示,P点的坐标可为:(0,0)或(0,) 或(4,0)
6. 在平行四边形问题中.边和对角线没有明确时,分情况讨论而产生多解
例6. (2012江西样卷 ( http: / / www.21cnjy.com ))如图2,在直角坐标系中,已知A(1,0)、B(-1,-2)、C(2,-2)三点坐标,若以A、B、C、D为顶点的四边形是平行四边形,那么点D的坐标可以是
评析:题图中由于AB、B ( http: / / www.21cnjy.com )C、AC是平行四边形的边还是对角线是不确定的,因此理所当然要分情况讨论,方法显然是分别以AB、BC、AC为对角线,结合平行四边形的对角线互相平分及其它相关性质易获得点D的坐标 .
本例是一道分类思路清晰,知识涉及较广,结构清爽的分类讨论题.
答案:(-2,0) (0,-4) (4,0)
7.在拼接问题中,拼接的方式没明确时,分情况讨 论而产生多解
例7.已知矩形的长为3,宽为1,现将四个这样的矩形用不同的方式拼成一个面积为12的大矩形,那么这个大矩形的周长是
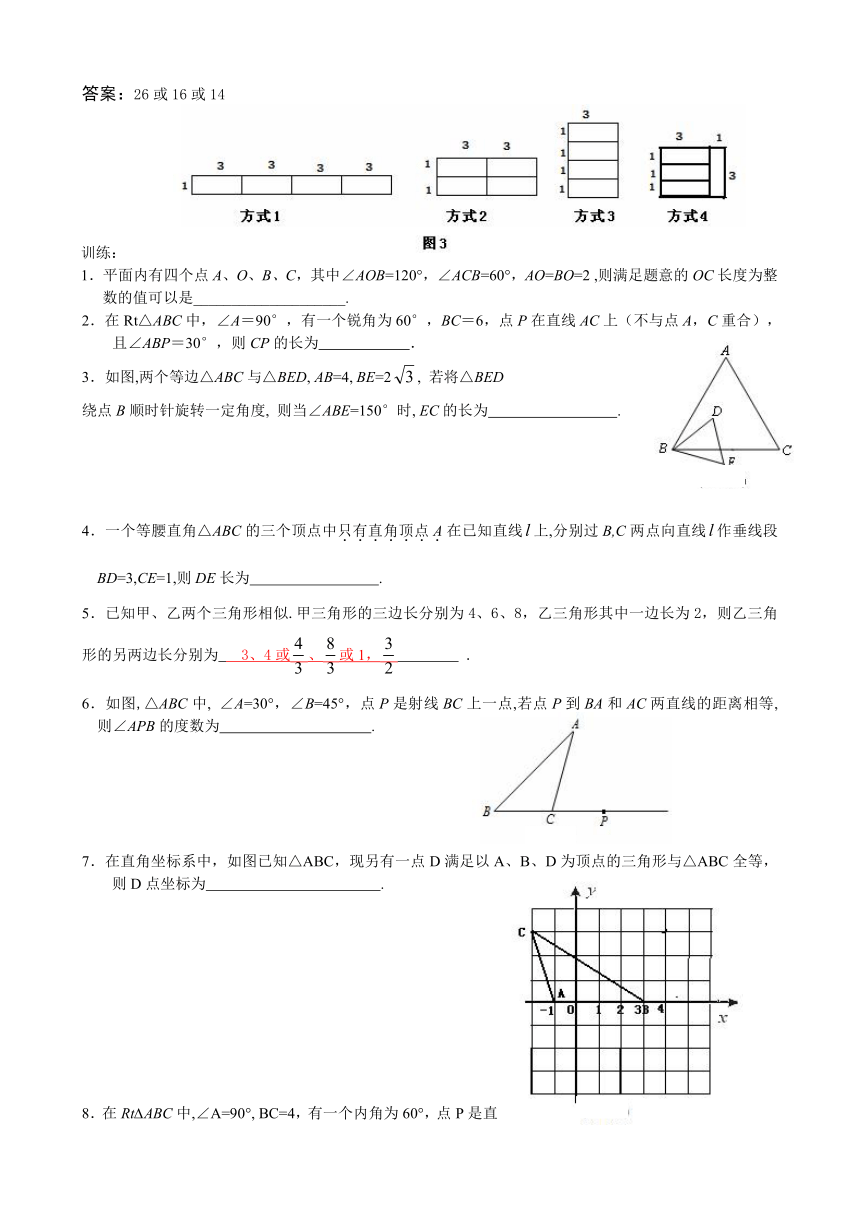
评析:本题分类的标准不太好明确,从实践操作中可发现有4种方法拼接成满足条件的大矩形,如图3:
答案:26或16或14
训练:
1.平面内有四个点A、O、B、C,其中 ( http: / / www.21cnjy.com )∠AOB=120°,∠ACB=60°,AO=BO=2 ,则满足题意的OC长度为整数的值可以是____________________.
2.在Rt△ABC中,∠A=90°,有 ( http: / / www.21cnjy.com )一个锐角为60°,BC=6,点P在直线AC上(不与点A,C重合),且∠ABP=30°,则CP的长为 .
3.如图,两个等边△ABC与△BED, AB=4, BE=2, 若将△BED
绕点B顺时针旋转一定角度, 则当∠ABE=150°时, EC的长为 .
4.一个等腰直角△ABC的三个顶点中只有直角顶点A在已知直线上,分别过B,C两点向直线作垂线段BD=3,CE=1,则DE长为 .
5.已知甲、乙两个三角形相似.甲三角形的三边长分别为4、6、8,乙三角形其中一边长为2,则乙三角形的另两边长分别为 3、4或、或1, .
6.如图,△ABC中, ∠A=30 ( http: / / www.21cnjy.com )°,∠B=45°,点P是射线BC上一点,若点P到BA和AC两直线的距离相等,则∠APB的度数为 .
7.在直角坐标系中,如图已知△ABC,现 ( http: / / www.21cnjy.com )另有一点D满足以A、B、D为顶点的三角形与△ABC全等,则D点坐标为 .
8.在Rt ABC中,∠A=90°, ( http: / / www.21cnjy.com ) BC=4,有一个内角为60°,点P是直线AB上不同于A、B的一点,且∠ACP=30°,则PB的长为________________.
9.二次函数的图象与坐标轴只有两个交点,则的值为 .
10.已知⊙O的直径为4cm,A是圆上一定点,弦BC长为cm (A,B,C三点均不重合),当△ABC为等腰三角形时,其底边上的高为 ㎝.
对于“满足条件的多解”题,远不止上述那 ( http: / / www.21cnjy.com )些方面存在,当然也不是只有小题才有多解,在综合题中也是常有出现,并且所涉及到分类讨论那部分其特点或本质也是相同的,就是处理方法或策略也完全一样.笔者希望同学们在复习备考中掌握其技能、技巧、做到举一反三、触类旁通,努力提高自己的思维能力,培养自己的思维的条理性、缜密性、科学性.这是我们师生共同追求的目标之一.
二、创新画(作)图题:
本题型是新增加在第三大 ( http: / / www.21cnjy.com )题(原第三大题中有3小题,今年调整为共4小题)之中,也有可能放在第二大题中,这类题不但是考查对相关图形的性质掌握和合情合理的推理能力,同时也是检查相关的操作能力.
1.不限工具,利用网格画出满足条件的图形
例8. (2012江西样卷)如图4,在 ( http: / / www.21cnjy.com )边长为1的正方形网格中画有一个圆心为O的半圆,请在网格中以O为圆心,画一个与已知半圆的半径不同,且面积相等的扇形.
评析:要画扇形,首先弄清所画扇形应满足哪些条件?①圆心为O,②面积为2,③半径必须大于2,④扇形要落在网格中.根据这些要求,结合扇形面积计算公式,定能确定扇形的半径长和它的圆心角的大小,在这个探索过程中,方法为“转化”,思维是“逆向”,考查的是“知识与能力”.
答案:
2. 只用单项工具,作出满足要求的图形
例9. 题a:(2012江西样卷)如图5 ( http: / / www.21cnjy.com ),AB=AC,AD⊥BC于点D,请你在△ABC内部,仅用圆规确定E、F两点,使∠BEC=∠BFC=90°.
题b:(2012江西样卷)如图6,四边形ABCD是一个等腰梯形,请直接在图中仅用直尺,准确画出它的对称轴.
评析:本例有两个小题,题a只 ( http: / / www.21cnjy.com )能用圆规作图,题b只能用直尺,这个要求是侧重对作图方法的探究考查.题a所要作的两点在以BC为直径的圆且在△ABC内部的一段弧上.要发现这一点,必须灵活运用等腰三角形和圆周角的性质定理.题b要作等腰梯形的对称轴,实际上就是作上、下底边的公共中垂线,故必须是找出两点,这两点分别到线段AD、BC的两端距离相等,具体作法如下答案图.
答案
3. 不限工具,将一个图形按要求进行分割
例10.把一个等边三角形分成四个等腰三角形,要求:1.除图a外再画出三种互不相同的分法,2.像图a一样,注明每个等腰顶角的度数.
( http: / / www.21cnjy.com )
评析:本题初看确有一点不好入手,但只要 ( http: / / www.21cnjy.com )静下心来,反复理清等边三角形的性质、判定,还是不难找到突破口,例如:应用等腰三角形的“三线合一”这个性质,把等边三角形分成两个全等的直角三角形,再由直角三角形斜边上的中线,可把直角三角形分成两个等腰三角形.这不就获得一种分割方法吗?当然这个题在构造上与传统的作图不同,考查的重点是如何灵活运用相关的知识探求出怎样分割,更重要的是还要考查学生的创新能力.
答案:
4.不限工具,已知一部分图形按要求添画或补充图形
例11. .如图8是由三个小正方形组成 ( http: / / www.21cnjy.com )的图形,现再给你一个同样的小正方形拼接在原图上,使原图形变为一个轴对称图形,请你分别在图a、b、c中画出不同的拼接方案,并画出对称轴.
( http: / / www.21cnjy.com )
评析:本题要从不同角度观察图形,结合对称 ( http: / / www.21cnjy.com )图形相关概念,展开想象力,找到需补充的部分.才能顺利添画对称轴,这类题目难度虽然不大,但要有一定空间想象力.
答案:
( http: / / www.21cnjy.com )
5. 不限工具,在数轴上找出表示无理数的点
例12.甲同学用如图9所示方法作出了C点,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O、A、C在同一数轴上,OB=OC.
( http: / / www.21cnjy.com )
(1)C点所表示的数是 ;
(2)仿照甲同学的做法,在如下所给数轴上描出表示-的点C.
评析:在甲同学的作图的启发下,先应构造一个斜边为的直角三角形,如:OA=2,AB=5,斜边OB为,于是在数轴上表示-点就不难确定.这类题虽比较常见,但既体现作图原理,又有运用数形结合的思想和构造法的探索经历.
答案:(1)点C表示数.
(2).如答图:
6. 不限工具,画出图形变换后(或前)的图形
例13.如图10,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)先作△ABC关于直线成轴对称的图形,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
评析:本题是画出变换后的图形,画图时关键是根据相应的变换性质找出对应顶点的位置.
答案: 如图:
通过上述例举,“创新画(作)图题”中的“创新 ( http: / / www.21cnjy.com )”两字.其意思是说这类题不完全是指传统的尺规作图题.“画”或“作”也不是本质,本质是放在如何“画”,怎样“作”的层面上,这类题是试题改革不断发展过程中涌现出来的又一新题型.此类题型形式多样,既灵活又简洁,可以充分考查学生的想象力和创造能力,在学生经历观察、分析、想象、推理、操作的过程中,不仅考查了学生掌握知识的情况,同时考查了学生的动手操作的能力.
在另一方面还需理解的是:它既保留了尺 ( http: / / www.21cnjy.com )规作图的严密的逻辑推理的要求,同时还需要结合几何推理,对所要作的图形进行作图原理的推究和作图方法的探索,这就是“创新画(作)图题”的特色之一.
训练:
1.如图,线段OA放置在正方形网格中,现请你分别在图1、图2中添画(工具只能用无刻度的直尺)射线OB,使tan∠OAB的值分别为3和1.
( http: / / www.21cnjy.com )
2..如图,等边△ABC和等边△ECD的边长相等,BC与CD两边在同一直线上,请根据如下要求,使用无刻度的直尺,通过连线的方式画图.
(1)在图1中画一个直角三角形;
(2)在图2中画出∠ACE的平分线.
( http: / / www.21cnjy.com )
3.如图,矩形ABCD中,点E在BC上,AE=CE,试分别在下列两个图中按要求使用无刻度的直尺画图.
(1)在图1中,画出∠DAE的平分线;
(2)在图2中,画出∠AEC的平分线.
4.如图,是由一个正方形和等腰直角三角 ( http: / / www.21cnjy.com )形组成的图形.试分别在图1和图2中,用无刻度的直尺通过连线的方式,在图1中画出一个小正方形;在图2中画出图形的对称轴,并在指定位置表示出来.
( http: / / www.21cnjy.com )
正方形 , 对称轴 .
三.以二次函数知识为主体的二次函数综合题:
《课程标准》对二次函数这一知识点的学习要 ( http: / / www.21cnjy.com )求比较高,它最能体现初中代数的综合性和能力性.因此二次函数在近几年中考试卷中已形成必不可少的题型,但有时只是把二次函数作为问题的背景,而真正探究的是三角形、四边形或其它些知识.所要考查的二次函数知识涉及得少之又少,因此今年对二次函数的考查角度有所调整,目的要将二次函数的性质和特征作为试题主体来考查,促使我们在复习中把二次函数作为最核心的内容之一来教学.
1.抛物线的顶点在另一抛物线上运动而引发的相关问题的探究
例14.甲、乙两同学对关于y、x的抛物线f: 进行探讨交流时,各得出一个结论.
甲同学:当抛物线f经过原点时,顶点在第三象限平分线所在的直线上;
乙同学:不论m取什么实数值,抛物线f顶点一定不在第四象限.
(1)请你求出抛物线f经过原点时m的值及顶点坐标,并说明甲同学的结论是否正确?
(2)乙同学的结论正确吗?若你认为 ( http: / / www.21cnjy.com )正确,请求出当实数m变化时,抛物线f顶点的纵横坐标之间的函数关系式,并说明顶点不在第四象限的理由;若你认为不正确,求出抛物线f顶点在第四象限时,m的取值范围.
评析:本例呈现形式新颖,它以学生交流 ( http: / / www.21cnjy.com )为背景,围绕抛物线f的顶点位置特征来探讨.题中设问是由特殊到一般,探究的内容是如何求出抛物线横坐标之间函数(二次函数)关系式,根据这个二次函数关系式分析抛物线f的顶点位置特征,因此这是一道典型的以二次函数知识为主体的综合性试题.
答案: (1)抛物线f经过原点时,=0 则:=0或
∴当m=-1时抛物线f表达式为 顶点(-1,-1),
当m=0时抛物线f表达式为, 顶点(0,0).
由于顶点(-1,-1)和顶点(0,0)都在第三象限的平分线所在的直线上,
∴甲同学结论正确,
(2)乙同学的结论正确.
∵抛物线f的解析式可变为
∴抛物线f的顶点为(m, ),若设抛物线f的顶点为(x,y)
则:,
∴抛物线f顶点的纵横坐标的函数关系式为:,
又由于抛物线的顶点为(-1,-1),与x轴的交点为(0,0),(-2,0),
抛物线开口向上.∴抛物线不可能在第四象限.
即:不论m取什么实数值,抛物线f顶点一定不在第四象限..
2.抛物线通过变换得到新抛物线,由此引起对新旧抛物线相互关系的问题探究
例15.已知抛物线的图象向上平移m个单位()得到的新抛物线过点(1,8).
(1)求m的值,并将平移后的抛物线解析式写成的形式;
(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数y的解析式,在所给的平面直角坐标系中直接画出简图,并直接写出y与之间关系式.
评析:这是一道典型的以二次函数知识为主体的二次函数综合题.题中将抛物线进行了先平移,再将其中部分翻折的两次变换,并要求写出变换后的图象的解析式,其中稍难理解的是第二次变换,因为有一部分图象不动,还是第一次变换后的图象,而在x轴下方部分沿x轴翻折,即翻折后的图象与原图象关于x轴对称,因此第二次变换后的函数是一个分段函数.
答案:(1)由题意可得
又点(1,8)在图象上
∴
∴ ∴
(2)
当x≤-3或x≥-1时,y=+2, 当-3<x<-1时,y=2-
3.由二次函数中的a、b、c值变化产生的不同图象的认识与探究
例16. 已知抛物线m、n的解析式分别是关于y与的关系式:.
(1)对上述两个抛物线说法正确的序号是 ;
①两条抛物线与y轴的交点一定不在x轴的上方
②在抛物线m、n中,可以将其中一条抛物线经过向上或向下平移得到另一条抛物线
③在抛物线m、n中,可以将其中一条抛物线经过向左或向右平移得到另一条抛物线
④两条抛物线的顶点之间的距离为1
(2)若这两条抛物线中,只有一条与x轴交于A、B(A点在左)两个不同的点,问是哪条抛物线经过A、B两点?为什么?并求出A、B两点的坐标.
评析:本题根据两个抛物线系数的特征,探讨两条抛物线的位置关系.解答时:要注意到两解析式中的“a、b”都相同,则两抛物线的开口大小、方向相同,对称轴也相同.怎样平移才能重合,一看就知道.再因,<0,可以判断两条抛物线与y轴的交点位置,同时推断两条抛物线与x轴的交点情况.因此这是一道以抛物线知识为主体的说理题.
答案:(1)①②④
(2)①抛物线n与x轴交于A、B两个不同的点.
方法1:∵不论m为何值时,,<0,那么两条抛物线与y轴的交点一定不在x轴的上方,只有当m=0时,抛物线m的顶点在原点,而抛物线n与x轴有两个交点,
除此之外两条抛物线与x轴都有两个不同的交点.
∴当这两条抛物线中,只有一条与x轴交于A、B(A点在左)两个不同的点时,这条是抛物线n.且解析式为;,
令=0,得=0时,解得,
∴A(-1,0),B(1,0).
方法2:∵, =6≥0
所以此抛物线与轴有一个或两个交点;又∵, = =>0,所以此函数与轴一定有两个不同的交点,又∵只有一条与x轴交于A、B(A点在左)两个不同的点,∴这条只有抛物线n经过A、B两点,此时m=0.
当时,,令=0,得=0时,解得,
∴A(-1,0),B(1,0).
4.利用二次函数的性质解决实际问题
例17. 某校七年级学生准备去购买《英 ( http: / / www.21cnjy.com )汉词典》一书,此书的标价为20元,现A,B两书店都有此书出售,A店按如下方法促销:若只购1本则按标价销售,若一次性购买多于1本,但不多于20本时,每多购1本,每本售价在标价的基础上优惠2%(例如买两本,每本价优惠2%;买3本每本价优惠4%,依此类推),若多于20本时,每本售价为12元;B书店一律按标价的7折销售.
(1)试分别写出在两书店购此书总价,与购书本数之间的函数关系式;
(2)若某班一次性购买多于20本时,那么去哪家书店购买更合算,为什么?若要一次性购买不多于20本时,先写出y(y=-)与购书本数x之间的函数式,画出其函数图象,再利用函数图象分析去哪家书店买更合算.
评析:本例首先要根据实际问题 ( http: / / www.21cnjy.com )中的数量关系,建立二次函数关系,进而利用二次函数的增减性解决相关的实际问题.这类题突出二次函数性质的应用,应该说从另一个角度来考查二次函数的核心内容.
答案:(1)设购买x本,则在A书店购书的总费用为
在B书店购书的总费用为=20×0.7x=14x
(2)当x>20时, 显然,
当0<X≤20时,y=-=+=
当=0时,x=0或16.
由图象可得:当时, y>0,当x=16时,y=0,当20>x>16时,y<0.
综上所述,若购书少于16本时,到B书店购买,
若购买16本,到A、B书店费用一样;
若超过16本,则到A书店购买合算.
仔细分析上述四例,与几何知识综合不多,全都是以二次函数知识为主线,从不同角度来评价学生对二次函数知识的掌握程度和应用能力.
这次对题型的调整,可以认为 ( http: / / www.21cnjy.com )是对知识板块侧重点的调整,丝毫没有放松对数学问题的本质和解题能力要求的考查,相反加强了对数形结合、分类讨论等思想方法和操作能力的考查.因此复习时注意总结体会各类数学习题中的思想方法,培养用数学思想方法解决问题的能力.
根据近年江西省试题特点,为了加强对多解题 ( http: / / www.21cnjy.com )、创新作图题和二次函数本质的考查题型的复习,有必要对此三类题型进行解读,以下对三类题型的一般类型及其解法进行例析.
一、满足条件的多解题:
满足条件的多解型试题不但知识覆盖面广,综合 ( http: / / www.21cnjy.com )性较强,题意构思精巧,而且在解答时需要灵活运用一种重要的数学思想方法——分类讨论,因此,这种题型今年不但在综合题中会有所涉及(往年常会出现),而且还规定把原来的多项选择型的第16题调整为一道“满足条件的多解”型题,对于这一调整笔者认为是进一步强调分类讨论这一思想方法考查,明确要求在复习中应加强对学生的多向思维的培养.同时也是为优化思维品质,克服思维的片面性,提高学生解题能力而出台一项具体措施.再则这类题的思维空间较大,解题时常出现考虑不全或不严谨,导致漏解、错解,因此我们应该熟练掌握这一题型的特征与解法.
1.在非负数问题中,是正是负没有明确时,分情况讨论而产生多解
例1. 已知a、b为实数,且ab≠0,那么= .
评析:本例是一道典型的分类讨论题.解答时首先根据公式“”把原式化为:,由于ab≠0即a、b都不为0,但a、b中哪个是正,哪个是负呢?所以只能分:①都是正;②都是负;③a为负,b为正;④a为正,b为负这四种情况来分别求值.
答案:0、2或-2
2.在一列数中,已知数与未知数没有明确大小时,分情况讨论而产生多解
例2.小明等五名同学四月份参加某次数学测验 ( http: / / www.21cnjy.com )(满分为120)的成绩如下:100、100、x、x、80.已知这组数据的中位数和平均数相等,那么整数x的值为 .
评析:由于一列数的中位数是 ( http: / / www.21cnjy.com )先按大小顺序排列后,最中间的那个数或最中间那两个数的平均值;题中x的大小有三种可能:①120≥x>100,②80<x≤100,③0≤x≤80,结合中位数、平均数的定义,可获得整数x值.本例抓住了x相对100和80大小可能性来分类,这种分类只要不漏掉某种情况,应该是不会出错的.
答案: 110或60(有一个非整数值已舍去)
3.在实际问题中,某方面的情境不明确时,分情况讨论而产生多解
例3.“五一”期间,某超市推出如下购物优惠方案:
一次性购物在100元(不含100元)以内时,不享受优惠;
(2)一次性购物在100元(含100元)以上,300元(不含300元)以内时一律享受九折的优惠;
(3)一次购物在300元(含300元)以上时,一律享受八折的优惠.
在此期间某顾客一次性购物付款252元,那么该顾客比平时购买总价相同的商品(没有优惠的时候)优惠了 元.
评析:题中情境有一个不明确的地方,即是:顾客优惠后的付款是252元,那么他所购买的商品的实际价格是在300元以下,还是多于300元呢?于是我们应分两种情况讨论.若是享受了优惠方案(2),则商品实价为=280元;若是享受了优惠方案(3),则商品实价为=315元.
像本例一样的问题,分类时,一定要按可能出现的情境来分类,否则会出现漏解现象,或者陷于无法入手的情形.
答案: 28或63.
4..在等腰三角形问题中,腰和底没有明确时,分情况讨论而产生多解
例4.已知,如图1:在平面直角坐标系中 ( http: / / www.21cnjy.com ),O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为 .
评析:题目给出了条件“△ODP是等腰三角形”,但未指明在△ODP中哪两条边相等,从而需要分情况考虑.但这里分类方法有几种:
如:方法1:OD、DP、OP轮流为底边,同时要注意以OD为底边时OP、PD是腰,但不会等于5,易产生错解,以OP为底边时又易漏掉一种情况.
方法2:∠POD、∠ODP、∠OP ( http: / / www.21cnjy.com )D轮流为顶角,这样分类同时还要考虑顶角可以是锐角、直角、钝角.本题由于腰为5的限制,故直角是不可能,∠POD为钝角不可能,∠PDO既可以是锐角,又可以为钝角.
方法3:由于腰为5,矩形的宽为4, ( http: / / www.21cnjy.com )易联想到勾3、股4、弦5,所以在OA上,在O点的右边取一点E,使OE=3,则OP=OD=5,在D点的左边取一点F,使DF=3,则OF=2,DP=OD=5,在D点的右边取一点G,使DG=3,则OG=8,DP=OD=5,这样P点坐标可直接写出.
这道题告诉我们,在抓住了分类讨论的特 ( http: / / www.21cnjy.com )征后,还要学会掌握分类的标准(或说方法).而有了分类的标准,就要自始至终使用这一标准分类,同时在求满足条件的点的坐标时,画出相应的图形,使用图形分析求解也是十分必要的,还有一点值得强调的是,分类后还应注意题中约束条件,谨防出现不合要求的解或漏解现象.
答案:(3,4),(2,4),(8,4).
5.在直角三角形问题中.直角边和斜边没有明确时,分情况讨论而产生多解
例5.线段AB的两端点的坐标为A(-1,0),B(0,-2)现请你在坐标轴上找一点P,
使得以P、A、B为顶点的三角形是直角三角形,则满足条件的P点的坐标是
评析:本例思考方法类似于例4,分类的标准也有几种,其中
可以分别以AB、AP、BP为斜边来确定P点的坐标.
答案:如图所示,P点的坐标可为:(0,0)或(0,) 或(4,0)
6. 在平行四边形问题中.边和对角线没有明确时,分情况讨论而产生多解
例6. (2012江西样卷 ( http: / / www.21cnjy.com ))如图2,在直角坐标系中,已知A(1,0)、B(-1,-2)、C(2,-2)三点坐标,若以A、B、C、D为顶点的四边形是平行四边形,那么点D的坐标可以是
评析:题图中由于AB、B ( http: / / www.21cnjy.com )C、AC是平行四边形的边还是对角线是不确定的,因此理所当然要分情况讨论,方法显然是分别以AB、BC、AC为对角线,结合平行四边形的对角线互相平分及其它相关性质易获得点D的坐标 .
本例是一道分类思路清晰,知识涉及较广,结构清爽的分类讨论题.
答案:(-2,0) (0,-4) (4,0)
7.在拼接问题中,拼接的方式没明确时,分情况讨 论而产生多解
例7.已知矩形的长为3,宽为1,现将四个这样的矩形用不同的方式拼成一个面积为12的大矩形,那么这个大矩形的周长是
评析:本题分类的标准不太好明确,从实践操作中可发现有4种方法拼接成满足条件的大矩形,如图3:
答案:26或16或14
训练:
1.平面内有四个点A、O、B、C,其中 ( http: / / www.21cnjy.com )∠AOB=120°,∠ACB=60°,AO=BO=2 ,则满足题意的OC长度为整数的值可以是____________________.
2.在Rt△ABC中,∠A=90°,有 ( http: / / www.21cnjy.com )一个锐角为60°,BC=6,点P在直线AC上(不与点A,C重合),且∠ABP=30°,则CP的长为 .
3.如图,两个等边△ABC与△BED, AB=4, BE=2, 若将△BED
绕点B顺时针旋转一定角度, 则当∠ABE=150°时, EC的长为 .
4.一个等腰直角△ABC的三个顶点中只有直角顶点A在已知直线上,分别过B,C两点向直线作垂线段BD=3,CE=1,则DE长为 .
5.已知甲、乙两个三角形相似.甲三角形的三边长分别为4、6、8,乙三角形其中一边长为2,则乙三角形的另两边长分别为 3、4或、或1, .
6.如图,△ABC中, ∠A=30 ( http: / / www.21cnjy.com )°,∠B=45°,点P是射线BC上一点,若点P到BA和AC两直线的距离相等,则∠APB的度数为 .
7.在直角坐标系中,如图已知△ABC,现 ( http: / / www.21cnjy.com )另有一点D满足以A、B、D为顶点的三角形与△ABC全等,则D点坐标为 .
8.在Rt ABC中,∠A=90°, ( http: / / www.21cnjy.com ) BC=4,有一个内角为60°,点P是直线AB上不同于A、B的一点,且∠ACP=30°,则PB的长为________________.
9.二次函数的图象与坐标轴只有两个交点,则的值为 .
10.已知⊙O的直径为4cm,A是圆上一定点,弦BC长为cm (A,B,C三点均不重合),当△ABC为等腰三角形时,其底边上的高为 ㎝.
对于“满足条件的多解”题,远不止上述那 ( http: / / www.21cnjy.com )些方面存在,当然也不是只有小题才有多解,在综合题中也是常有出现,并且所涉及到分类讨论那部分其特点或本质也是相同的,就是处理方法或策略也完全一样.笔者希望同学们在复习备考中掌握其技能、技巧、做到举一反三、触类旁通,努力提高自己的思维能力,培养自己的思维的条理性、缜密性、科学性.这是我们师生共同追求的目标之一.
二、创新画(作)图题:
本题型是新增加在第三大 ( http: / / www.21cnjy.com )题(原第三大题中有3小题,今年调整为共4小题)之中,也有可能放在第二大题中,这类题不但是考查对相关图形的性质掌握和合情合理的推理能力,同时也是检查相关的操作能力.
1.不限工具,利用网格画出满足条件的图形
例8. (2012江西样卷)如图4,在 ( http: / / www.21cnjy.com )边长为1的正方形网格中画有一个圆心为O的半圆,请在网格中以O为圆心,画一个与已知半圆的半径不同,且面积相等的扇形.
评析:要画扇形,首先弄清所画扇形应满足哪些条件?①圆心为O,②面积为2,③半径必须大于2,④扇形要落在网格中.根据这些要求,结合扇形面积计算公式,定能确定扇形的半径长和它的圆心角的大小,在这个探索过程中,方法为“转化”,思维是“逆向”,考查的是“知识与能力”.
答案:
2. 只用单项工具,作出满足要求的图形
例9. 题a:(2012江西样卷)如图5 ( http: / / www.21cnjy.com ),AB=AC,AD⊥BC于点D,请你在△ABC内部,仅用圆规确定E、F两点,使∠BEC=∠BFC=90°.
题b:(2012江西样卷)如图6,四边形ABCD是一个等腰梯形,请直接在图中仅用直尺,准确画出它的对称轴.
评析:本例有两个小题,题a只 ( http: / / www.21cnjy.com )能用圆规作图,题b只能用直尺,这个要求是侧重对作图方法的探究考查.题a所要作的两点在以BC为直径的圆且在△ABC内部的一段弧上.要发现这一点,必须灵活运用等腰三角形和圆周角的性质定理.题b要作等腰梯形的对称轴,实际上就是作上、下底边的公共中垂线,故必须是找出两点,这两点分别到线段AD、BC的两端距离相等,具体作法如下答案图.
答案
3. 不限工具,将一个图形按要求进行分割
例10.把一个等边三角形分成四个等腰三角形,要求:1.除图a外再画出三种互不相同的分法,2.像图a一样,注明每个等腰顶角的度数.
( http: / / www.21cnjy.com )
评析:本题初看确有一点不好入手,但只要 ( http: / / www.21cnjy.com )静下心来,反复理清等边三角形的性质、判定,还是不难找到突破口,例如:应用等腰三角形的“三线合一”这个性质,把等边三角形分成两个全等的直角三角形,再由直角三角形斜边上的中线,可把直角三角形分成两个等腰三角形.这不就获得一种分割方法吗?当然这个题在构造上与传统的作图不同,考查的重点是如何灵活运用相关的知识探求出怎样分割,更重要的是还要考查学生的创新能力.
答案:
4.不限工具,已知一部分图形按要求添画或补充图形
例11. .如图8是由三个小正方形组成 ( http: / / www.21cnjy.com )的图形,现再给你一个同样的小正方形拼接在原图上,使原图形变为一个轴对称图形,请你分别在图a、b、c中画出不同的拼接方案,并画出对称轴.
( http: / / www.21cnjy.com )
评析:本题要从不同角度观察图形,结合对称 ( http: / / www.21cnjy.com )图形相关概念,展开想象力,找到需补充的部分.才能顺利添画对称轴,这类题目难度虽然不大,但要有一定空间想象力.
答案:
( http: / / www.21cnjy.com )
5. 不限工具,在数轴上找出表示无理数的点
例12.甲同学用如图9所示方法作出了C点,在△OAB中,∠OAB=90°,OA=2,AB=3,且点O、A、C在同一数轴上,OB=OC.
( http: / / www.21cnjy.com )
(1)C点所表示的数是 ;
(2)仿照甲同学的做法,在如下所给数轴上描出表示-的点C.
评析:在甲同学的作图的启发下,先应构造一个斜边为的直角三角形,如:OA=2,AB=5,斜边OB为,于是在数轴上表示-点就不难确定.这类题虽比较常见,但既体现作图原理,又有运用数形结合的思想和构造法的探索经历.
答案:(1)点C表示数.
(2).如答图:
6. 不限工具,画出图形变换后(或前)的图形
例13.如图10,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;
(1)先作△ABC关于直线成轴对称的图形,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
评析:本题是画出变换后的图形,画图时关键是根据相应的变换性质找出对应顶点的位置.
答案: 如图:
通过上述例举,“创新画(作)图题”中的“创新 ( http: / / www.21cnjy.com )”两字.其意思是说这类题不完全是指传统的尺规作图题.“画”或“作”也不是本质,本质是放在如何“画”,怎样“作”的层面上,这类题是试题改革不断发展过程中涌现出来的又一新题型.此类题型形式多样,既灵活又简洁,可以充分考查学生的想象力和创造能力,在学生经历观察、分析、想象、推理、操作的过程中,不仅考查了学生掌握知识的情况,同时考查了学生的动手操作的能力.
在另一方面还需理解的是:它既保留了尺 ( http: / / www.21cnjy.com )规作图的严密的逻辑推理的要求,同时还需要结合几何推理,对所要作的图形进行作图原理的推究和作图方法的探索,这就是“创新画(作)图题”的特色之一.
训练:
1.如图,线段OA放置在正方形网格中,现请你分别在图1、图2中添画(工具只能用无刻度的直尺)射线OB,使tan∠OAB的值分别为3和1.
( http: / / www.21cnjy.com )
2..如图,等边△ABC和等边△ECD的边长相等,BC与CD两边在同一直线上,请根据如下要求,使用无刻度的直尺,通过连线的方式画图.
(1)在图1中画一个直角三角形;
(2)在图2中画出∠ACE的平分线.
( http: / / www.21cnjy.com )
3.如图,矩形ABCD中,点E在BC上,AE=CE,试分别在下列两个图中按要求使用无刻度的直尺画图.
(1)在图1中,画出∠DAE的平分线;
(2)在图2中,画出∠AEC的平分线.
4.如图,是由一个正方形和等腰直角三角 ( http: / / www.21cnjy.com )形组成的图形.试分别在图1和图2中,用无刻度的直尺通过连线的方式,在图1中画出一个小正方形;在图2中画出图形的对称轴,并在指定位置表示出来.
( http: / / www.21cnjy.com )
正方形 , 对称轴 .
三.以二次函数知识为主体的二次函数综合题:
《课程标准》对二次函数这一知识点的学习要 ( http: / / www.21cnjy.com )求比较高,它最能体现初中代数的综合性和能力性.因此二次函数在近几年中考试卷中已形成必不可少的题型,但有时只是把二次函数作为问题的背景,而真正探究的是三角形、四边形或其它些知识.所要考查的二次函数知识涉及得少之又少,因此今年对二次函数的考查角度有所调整,目的要将二次函数的性质和特征作为试题主体来考查,促使我们在复习中把二次函数作为最核心的内容之一来教学.
1.抛物线的顶点在另一抛物线上运动而引发的相关问题的探究
例14.甲、乙两同学对关于y、x的抛物线f: 进行探讨交流时,各得出一个结论.
甲同学:当抛物线f经过原点时,顶点在第三象限平分线所在的直线上;
乙同学:不论m取什么实数值,抛物线f顶点一定不在第四象限.
(1)请你求出抛物线f经过原点时m的值及顶点坐标,并说明甲同学的结论是否正确?
(2)乙同学的结论正确吗?若你认为 ( http: / / www.21cnjy.com )正确,请求出当实数m变化时,抛物线f顶点的纵横坐标之间的函数关系式,并说明顶点不在第四象限的理由;若你认为不正确,求出抛物线f顶点在第四象限时,m的取值范围.
评析:本例呈现形式新颖,它以学生交流 ( http: / / www.21cnjy.com )为背景,围绕抛物线f的顶点位置特征来探讨.题中设问是由特殊到一般,探究的内容是如何求出抛物线横坐标之间函数(二次函数)关系式,根据这个二次函数关系式分析抛物线f的顶点位置特征,因此这是一道典型的以二次函数知识为主体的综合性试题.
答案: (1)抛物线f经过原点时,=0 则:=0或
∴当m=-1时抛物线f表达式为 顶点(-1,-1),
当m=0时抛物线f表达式为, 顶点(0,0).
由于顶点(-1,-1)和顶点(0,0)都在第三象限的平分线所在的直线上,
∴甲同学结论正确,
(2)乙同学的结论正确.
∵抛物线f的解析式可变为
∴抛物线f的顶点为(m, ),若设抛物线f的顶点为(x,y)
则:,
∴抛物线f顶点的纵横坐标的函数关系式为:,
又由于抛物线的顶点为(-1,-1),与x轴的交点为(0,0),(-2,0),
抛物线开口向上.∴抛物线不可能在第四象限.
即:不论m取什么实数值,抛物线f顶点一定不在第四象限..
2.抛物线通过变换得到新抛物线,由此引起对新旧抛物线相互关系的问题探究
例15.已知抛物线的图象向上平移m个单位()得到的新抛物线过点(1,8).
(1)求m的值,并将平移后的抛物线解析式写成的形式;
(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数y的解析式,在所给的平面直角坐标系中直接画出简图,并直接写出y与之间关系式.
评析:这是一道典型的以二次函数知识为主体的二次函数综合题.题中将抛物线进行了先平移,再将其中部分翻折的两次变换,并要求写出变换后的图象的解析式,其中稍难理解的是第二次变换,因为有一部分图象不动,还是第一次变换后的图象,而在x轴下方部分沿x轴翻折,即翻折后的图象与原图象关于x轴对称,因此第二次变换后的函数是一个分段函数.
答案:(1)由题意可得
又点(1,8)在图象上
∴
∴ ∴
(2)
当x≤-3或x≥-1时,y=+2, 当-3<x<-1时,y=2-
3.由二次函数中的a、b、c值变化产生的不同图象的认识与探究
例16. 已知抛物线m、n的解析式分别是关于y与的关系式:.
(1)对上述两个抛物线说法正确的序号是 ;
①两条抛物线与y轴的交点一定不在x轴的上方
②在抛物线m、n中,可以将其中一条抛物线经过向上或向下平移得到另一条抛物线
③在抛物线m、n中,可以将其中一条抛物线经过向左或向右平移得到另一条抛物线
④两条抛物线的顶点之间的距离为1
(2)若这两条抛物线中,只有一条与x轴交于A、B(A点在左)两个不同的点,问是哪条抛物线经过A、B两点?为什么?并求出A、B两点的坐标.
评析:本题根据两个抛物线系数的特征,探讨两条抛物线的位置关系.解答时:要注意到两解析式中的“a、b”都相同,则两抛物线的开口大小、方向相同,对称轴也相同.怎样平移才能重合,一看就知道.再因,<0,可以判断两条抛物线与y轴的交点位置,同时推断两条抛物线与x轴的交点情况.因此这是一道以抛物线知识为主体的说理题.
答案:(1)①②④
(2)①抛物线n与x轴交于A、B两个不同的点.
方法1:∵不论m为何值时,,<0,那么两条抛物线与y轴的交点一定不在x轴的上方,只有当m=0时,抛物线m的顶点在原点,而抛物线n与x轴有两个交点,
除此之外两条抛物线与x轴都有两个不同的交点.
∴当这两条抛物线中,只有一条与x轴交于A、B(A点在左)两个不同的点时,这条是抛物线n.且解析式为;,
令=0,得=0时,解得,
∴A(-1,0),B(1,0).
方法2:∵, =6≥0
所以此抛物线与轴有一个或两个交点;又∵, = =>0,所以此函数与轴一定有两个不同的交点,又∵只有一条与x轴交于A、B(A点在左)两个不同的点,∴这条只有抛物线n经过A、B两点,此时m=0.
当时,,令=0,得=0时,解得,
∴A(-1,0),B(1,0).
4.利用二次函数的性质解决实际问题
例17. 某校七年级学生准备去购买《英 ( http: / / www.21cnjy.com )汉词典》一书,此书的标价为20元,现A,B两书店都有此书出售,A店按如下方法促销:若只购1本则按标价销售,若一次性购买多于1本,但不多于20本时,每多购1本,每本售价在标价的基础上优惠2%(例如买两本,每本价优惠2%;买3本每本价优惠4%,依此类推),若多于20本时,每本售价为12元;B书店一律按标价的7折销售.
(1)试分别写出在两书店购此书总价,与购书本数之间的函数关系式;
(2)若某班一次性购买多于20本时,那么去哪家书店购买更合算,为什么?若要一次性购买不多于20本时,先写出y(y=-)与购书本数x之间的函数式,画出其函数图象,再利用函数图象分析去哪家书店买更合算.
评析:本例首先要根据实际问题 ( http: / / www.21cnjy.com )中的数量关系,建立二次函数关系,进而利用二次函数的增减性解决相关的实际问题.这类题突出二次函数性质的应用,应该说从另一个角度来考查二次函数的核心内容.
答案:(1)设购买x本,则在A书店购书的总费用为
在B书店购书的总费用为=20×0.7x=14x
(2)当x>20时, 显然,
当0<X≤20时,y=-=+=
当=0时,x=0或16.
由图象可得:当时, y>0,当x=16时,y=0,当20>x>16时,y<0.
综上所述,若购书少于16本时,到B书店购买,
若购买16本,到A、B书店费用一样;
若超过16本,则到A书店购买合算.
仔细分析上述四例,与几何知识综合不多,全都是以二次函数知识为主线,从不同角度来评价学生对二次函数知识的掌握程度和应用能力.
这次对题型的调整,可以认为 ( http: / / www.21cnjy.com )是对知识板块侧重点的调整,丝毫没有放松对数学问题的本质和解题能力要求的考查,相反加强了对数形结合、分类讨论等思想方法和操作能力的考查.因此复习时注意总结体会各类数学习题中的思想方法,培养用数学思想方法解决问题的能力.
同课章节目录
