2.2.3直线与平面平行的性质(广东省东莞市)
文档属性
| 名称 | 2.2.3直线与平面平行的性质(广东省东莞市) |  | |
| 格式 | rar | ||
| 文件大小 | 228.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-04 07:13:00 | ||
图片预览


文档简介
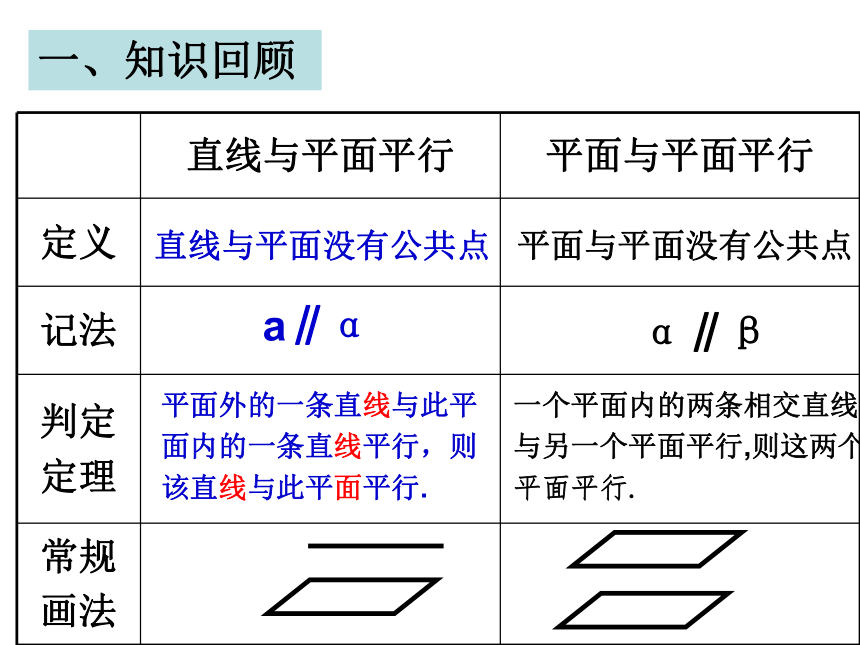
课件14张PPT。直线与平面平行的性质一、知识回顾直线与平面没有公共点a∥α平面外的一条直线与此平
面内的一条直线平行,则
该直线与此平面平行.平面与平面没有公共点α∥β一个平面内的两条相交直线
与另一个平面平行,则这两个
平面平行.空间中直线与直线平行的判定方法1.定义:在同一平面内,没有公共点的两条直线
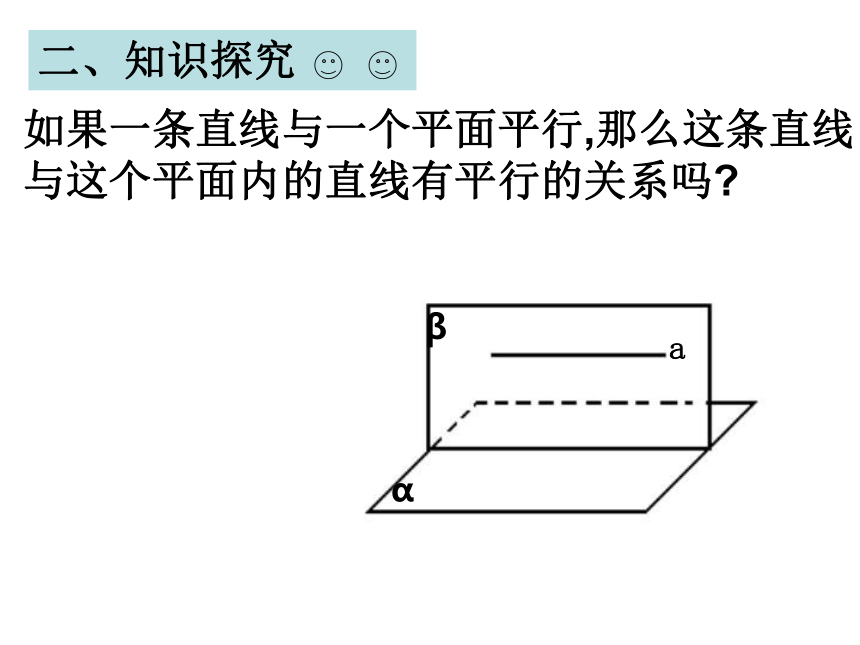
是平行直线.2.公理4:平行于同一直线的两条直线互相平行一、知识回顾二、知识探究如果一条直线与一个平面平行,那么这条直线
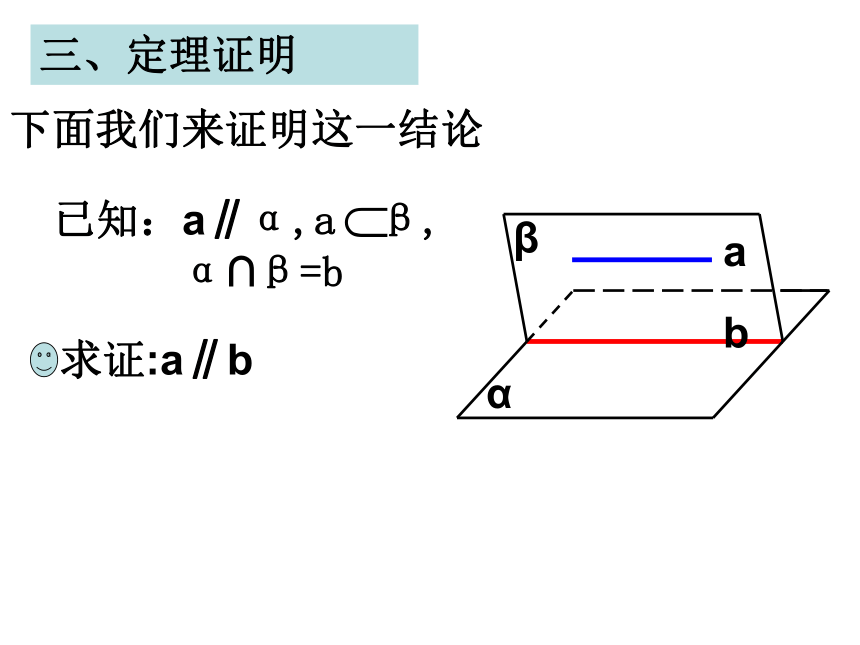
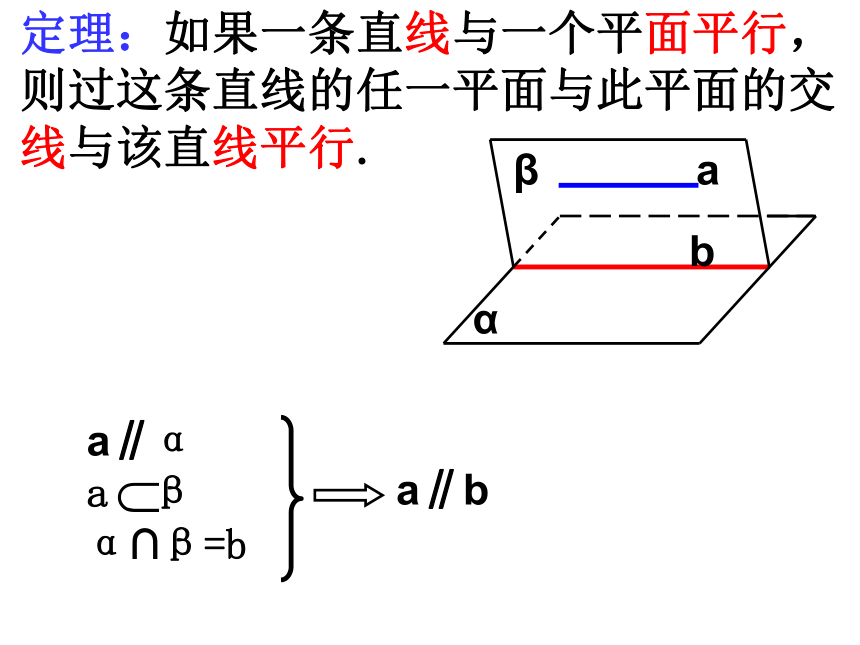
与这个平面内的直线有平行的关系吗?β下面我们来证明这一结论三、定理证明abαβ求证:a∥b定理:如果一条直线与一个平面平行,
则过这条直线的任一平面与此平面的交
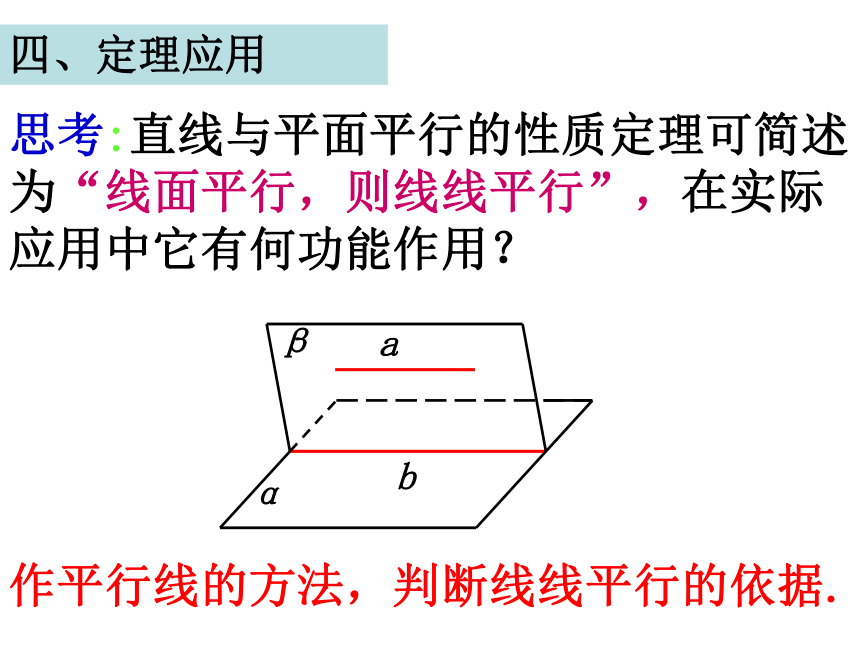
线与该直线平行. abαβa∥b思考:直线与平面平行的性质定理可简述为“线面平行,则线线平行”,在实际应用中它有何功能作用?作平行线的方法,判断线线平行的依据. 四、定理应用P58思考(2):教室内日光灯管所在的直线与地面平行,如何在地面上作一条直线与灯管所在的直线平行? 例4 已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面.abα已知:如图,已知直线a,b和平面α ,a∥b,a∥α , a,b都在平面α外 .
求证:b∥α . 证明:过a作平面β,使它与平面α相交,
交线为cabα∴a∥c∵a∥b∴b∥c∴b∥a例3 如图所示的一块木料中,棱BC平行
于面A′C′.
(1)要经过面A′C′ 内一点P和棱BC将
木料锯开,应怎样画线?
(2)所画的线与平面AC是什么位置关系? 五、课堂小结线线平行线面平行直线与平面平行的判定直线与平面平行的性质1、转化思想2、线线平行的证明方法(1)定义(2)公理4(3)直线与平面平行的性质在空间四边形ABCD中,E,F,G,H分别为AC,BC,BD,AD上的点,若四边形EFGH为平行四边形。求证:AB∥平面EFGH。六、巩固提高ABCDA1B1C1D1
面内的一条直线平行,则
该直线与此平面平行.平面与平面没有公共点α∥β一个平面内的两条相交直线
与另一个平面平行,则这两个
平面平行.空间中直线与直线平行的判定方法1.定义:在同一平面内,没有公共点的两条直线
是平行直线.2.公理4:平行于同一直线的两条直线互相平行一、知识回顾二、知识探究如果一条直线与一个平面平行,那么这条直线
与这个平面内的直线有平行的关系吗?β下面我们来证明这一结论三、定理证明abαβ求证:a∥b定理:如果一条直线与一个平面平行,
则过这条直线的任一平面与此平面的交
线与该直线平行. abαβa∥b思考:直线与平面平行的性质定理可简述为“线面平行,则线线平行”,在实际应用中它有何功能作用?作平行线的方法,判断线线平行的依据. 四、定理应用P58思考(2):教室内日光灯管所在的直线与地面平行,如何在地面上作一条直线与灯管所在的直线平行? 例4 已知平面外的两条平行直线中的一条平行于这个平面,求证:另一条也平行于这个平面.abα已知:如图,已知直线a,b和平面α ,a∥b,a∥α , a,b都在平面α外 .
求证:b∥α . 证明:过a作平面β,使它与平面α相交,
交线为cabα∴a∥c∵a∥b∴b∥c∴b∥a例3 如图所示的一块木料中,棱BC平行
于面A′C′.
(1)要经过面A′C′ 内一点P和棱BC将
木料锯开,应怎样画线?
(2)所画的线与平面AC是什么位置关系? 五、课堂小结线线平行线面平行直线与平面平行的判定直线与平面平行的性质1、转化思想2、线线平行的证明方法(1)定义(2)公理4(3)直线与平面平行的性质在空间四边形ABCD中,E,F,G,H分别为AC,BC,BD,AD上的点,若四边形EFGH为平行四边形。求证:AB∥平面EFGH。六、巩固提高ABCDA1B1C1D1
