2024沪科版数学八年级下学期--第18章《勾股定理》素养综合检测(含解析)
文档属性
| 名称 | 2024沪科版数学八年级下学期--第18章《勾股定理》素养综合检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 477.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024沪科版数学八年级下学期
第18章 勾股定理
第18章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.(2023安徽合肥瑶海期中)以下列各组数为边长,能构成直角三角形的是( )
A.1,1,2 B.2,3,4
C.4,5,6 D.1,,2
2.在下列四组数中,不是勾股数的一组数是( )
A.8,15,17 B.6,8,10
C.5,12,13 D.3,5,7
3.【新独家原创】晓波在练习本上画了四个直角三角形,并分别以这四个三角形的三边为边向外作正方形.若每个正方形中的数字及字母S分别表示所在正方形的面积,那么S的值恰好等于1的是( )
A B C D
4.(2023安徽黄山休宁期中)如图,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为( )
A.米 B.米
C.(+1)米 D.3米
5.(2022安徽安庆期中)直角三角形中一直角边的长为9,另两边的长为连续自然数,则直角三角形的周长为( )
A.121 B.120
C.90 D.不能确定
6.若△ABC的三边长a、b、c满足(a-b)2+|a2+b2-c2|=0,则△ABC是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
7.(2022安徽合肥五十中月考)下列说法中,错误的是( )
A.在△ABC中,若∠C=∠B=∠A,则△ABC是直角三角形
B.在△ABC中,若∠A∶∠B∶∠C=3∶4∶5,则△ABC是直角三角形
C.在△ABC中,若∠A=∠B-∠C,则△ABC是直角三角形
D.在△ABC中,若三边长a,b,c满足a∶b∶c=1∶2∶,则△ABC是直角三角形
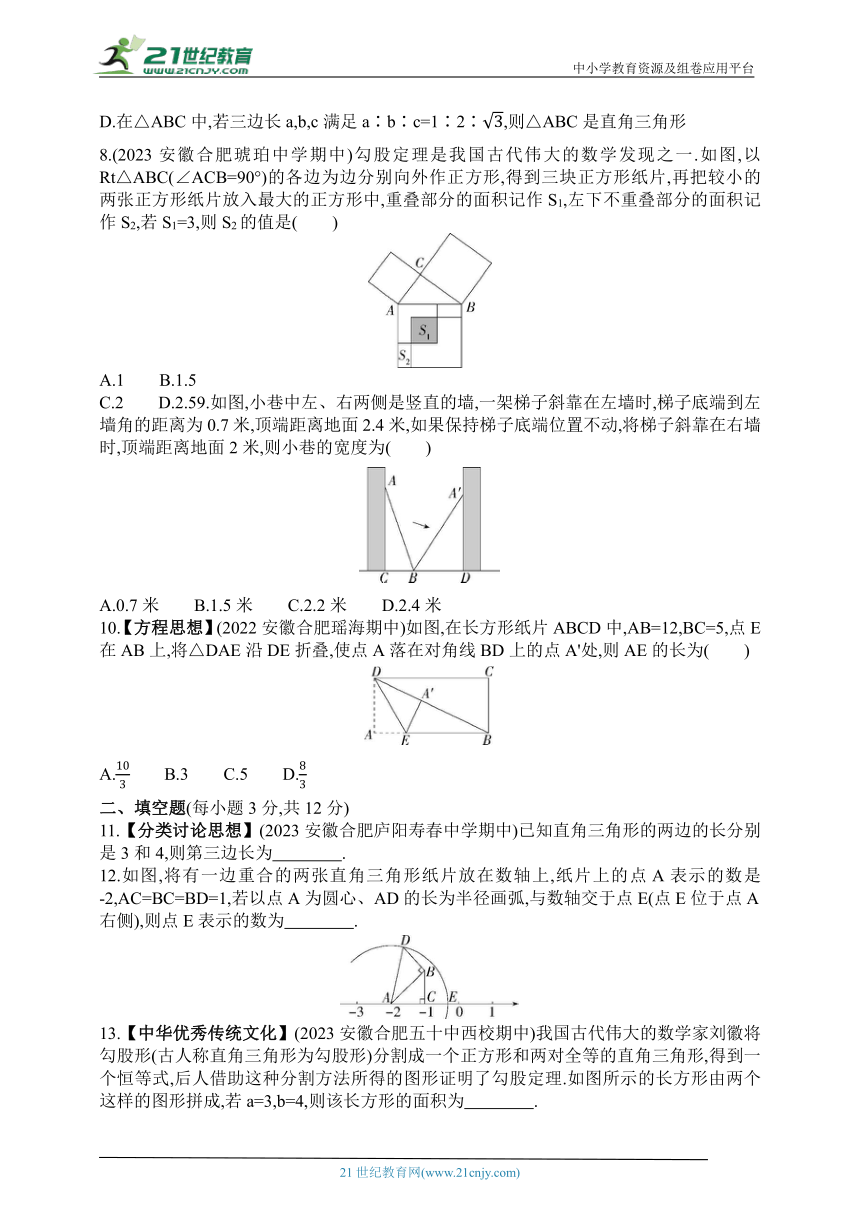
8.(2023安徽合肥琥珀中学期中)勾股定理是我国古代伟大的数学发现之一.如图,以Rt△ABC(∠ACB=90°)的各边为边分别向外作正方形,得到三块正方形纸片,再把较小的两张正方形纸片放入最大的正方形中,重叠部分的面积记作S1,左下不重叠部分的面积记作S2,若S1=3,则S2的值是( )
A.1 B.1.5
C.2 D.2.59.如图,小巷中左、右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米 B.1.5米 C.2.2米 D.2.4米
10.【方程思想】(2022安徽合肥瑶海期中)如图,在长方形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A'处,则AE的长为( )
A. B.3 C.5 D.
二、填空题(每小题3分,共12分)
11.【分类讨论思想】(2023安徽合肥庐阳寿春中学期中)已知直角三角形的两边的长分别是3和4,则第三边长为 .
12.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2,AC=BC=BD=1,若以点A为圆心、AD的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为 .
13.【中华优秀传统文化】(2023安徽合肥五十中西校期中)我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示的长方形由两个这样的图形拼成,若a=3,b=4,则该长方形的面积为 .
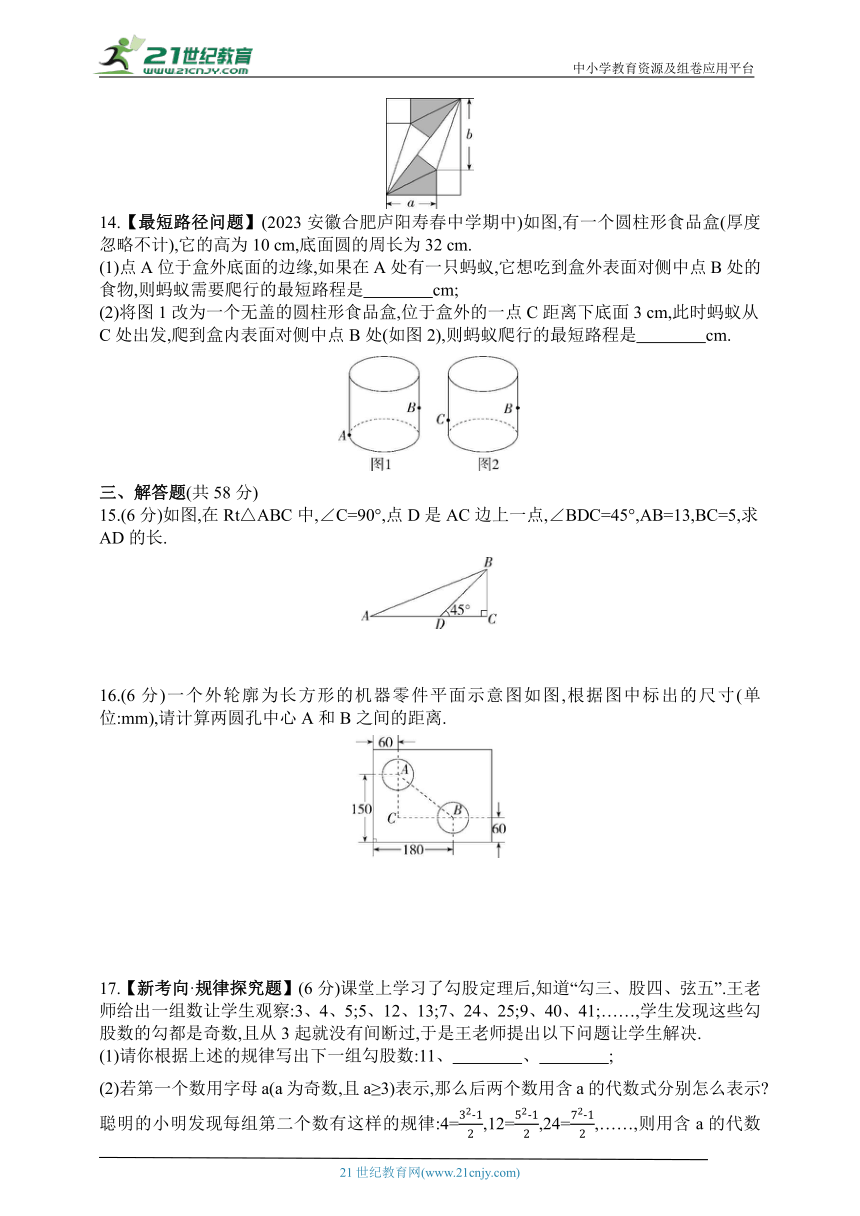
14.【最短路径问题】(2023安徽合肥庐阳寿春中学期中)如图,有一个圆柱形食品盒(厚度忽略不计),它的高为10 cm,底面圆的周长为32 cm.
(1)点A位于盒外底面的边缘,如果在A处有一只蚂蚁,它想吃到盒外表面对侧中点B处的食物,则蚂蚁需要爬行的最短路程是 cm;
(2)将图1改为一个无盖的圆柱形食品盒,位于盒外的一点C距离下底面3 cm,此时蚂蚁从C处出发,爬到盒内表面对侧中点B处(如图2),则蚂蚁爬行的最短路程是 cm.
三、解答题(共58分)
15.(6分)如图,在Rt△ABC中,∠C=90°,点D是AC边上一点,∠BDC=45°,AB=13,BC=5,求AD的长.
16.(6分)一个外轮廓为长方形的机器零件平面示意图如图,根据图中标出的尺寸(单位:mm),请计算两圆孔中心A和B之间的距离.
17.【新考向·规律探究题】(6分)课堂上学习了勾股定理后,知道“勾三、股四、弦五”.王老师给出一组数让学生观察:3、4、5;5、12、13;7、24、25;9、40、41;……,学生发现这些勾股数的勾都是奇数,且从3起就没有间断过,于是王老师提出以下问题让学生解决.
(1)请你根据上述的规律写出下一组勾股数:11、 、 ;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别怎么表示 聪明的小明发现每组第二个数有这样的规律:4=,12=,24=,……,则用含a的代数式表示每组第二个数和第三个数分别为 、 ,并用所学知识加以证明.
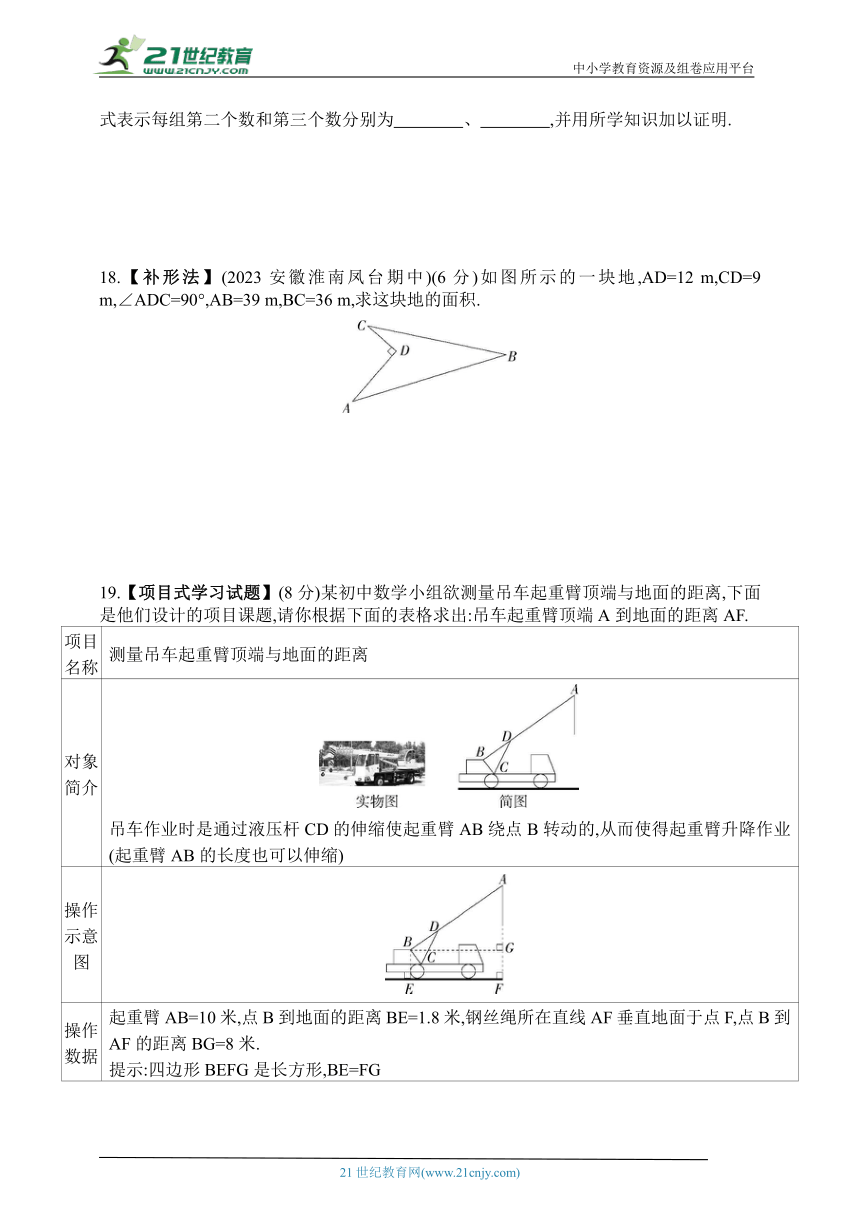
18.【补形法】(2023安徽淮南凤台期中)(6分)如图所示的一块地,AD=12 m,CD=9 m,∠ADC=90°,AB=39 m,BC=36 m,求这块地的面积.
19.【项目式学习试题】(8分)某初中数学小组欲测量吊车起重臂顶端与地面的距离,下面是他们设计的项目课题,请你根据下面的表格求出:吊车起重臂顶端A到地面的距离AF.
项目 名称 测量吊车起重臂顶端与地面的距离
对象 简介 吊车作业时是通过液压杆CD的伸缩使起重臂AB绕点B转动的,从而使得起重臂升降作业(起重臂AB的长度也可以伸缩)
操作 示意 图
操作 数据 起重臂AB=10米,点B到地面的距离BE=1.8米,钢丝绳所在直线AF垂直地面于点F,点B到AF的距离BG=8米. 提示:四边形BEFG是长方形,BE=FG
20.【分割法】【教材变式·P60T3】(2023安徽合肥琥珀中学期中)(8分)为了绿化环境,我市某中学有一块四边形的空地ABCD,如图.学校计划在空地上种植草皮,经测量∠A=90°,AB=9 m,DA=12 m,BC=8 m,CD=17 m.
(1)求空地ABCD的面积.
(2)若每种植1平方米草皮需要350元,问总共需投入多少元
21.(8分)拖拉机行驶过程中会对周围产生较大的噪声影响.如图,有一台拖拉机沿公路AB由点A向点B行驶,AB=250 m,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为150 m和200 m,拖拉机周围130 m以内为受噪声影响区域.
(1)求∠ACB的度数.
(2)学校C会受噪声影响吗 为什么
(3)若学校受拖拉机噪声影响,拖拉机的行驶速度为每分钟50 m,则拖拉机噪声影响该学校持续的时间为多少分钟
22.(10分)如图,在Rt△ABC中,∠B=90°,AB=6 cm,BC=10 cm,点P从点A开始沿AB边向点B移动,速度为1 cm/s;点Q从点B开始沿BC边向点C移动,速度为2 cm/s,点P、Q分别从点A、B同时出发,当其中一点到达终点时,另一点也随之停止运动.
(1)几秒后,PQ的长度为3 cm
(2)几秒后,△PBQ的面积为8 cm2
(3)△PBQ的面积能不能是14 cm2 请说明理由.
第18章 勾股定理
第18章 素养综合检测
答案全解全析
1.D 12+12≠22,22+32≠42,42+52≠62,均不能构成直角三角形,故选项A、B、C不符合题意;12+()2=22,能构成直角三角形,故选项D符合题意.
2.D 82+152=172,且都是正整数,是勾股数,选项A不符合题意;62+82=102,且都是正整数,是勾股数,选项B不符合题意;52+122=132,且都是正整数,是勾股数,选项C不符合题意;32+52≠72,不是勾股数,选项D符合题意.
3.D ∵每个正方形中的数字及字母S表示所在正方形的面积,∴每个正方形中的数字以及字母S表示所在正方形的边长的平方.选项A中,由勾股定理得S=4+9=13,故选项A不符合题意;选项B中,S=9-4=5,故选项B不符合题意;选项C中,S=4+3=7,故选项C不符合题意;选项D中,S=4-3=1,故选项D符合题意.
4.C 在Rt△ACB中,根据勾股定理可求得BC==米,∴树的高度:AC+BC=(+1)米,故选C.
5.C 设另一直角边的长为a,则斜边的长为a+1.
根据勾股定理得(a+1)2-a2=92,
解得a=40,则a+1=41,
所以直角三角形的周长为9+40+41=90.
6.C ∵(a-b)2+|a2+b2-c2|=0,
∴a-b=0,a2+b2-c2=0,∴a=b,a2+b2=c2,
∴△ABC为等腰直角三角形.故选C.
7.B 在△ABC中,若∠C=∠B=∠A,则∠A+∠B+∠C=3∠C+2∠C+∠C=6∠C=180°,∴∠A=3∠C=90°,是直角三角形,选项A不符合题意;在△ABC中,若∠A∶∠B∶∠C=3∶4∶5,则最大角∠C=180°×=75°,不是直角三角形,选项B符合题意;在△ABC中,若∠A=∠B-∠C,则∠B=∠A+∠C=90°,是直角三角形,选项C不符合题意;∵12+()2=22,∴△ABC是直角三角形,选项D不符合题意.
8.B 设Rt△ABC的直角边AC=a,BC=b,BA=c,∴a2+b2=c2.∵面积为S2的长方形的长和宽分别是c-a,c-b,∴S2=(c-a)(c-b)=c2-(a+b)c+ab.∵面积为S1的正方形的边长是a+b-c,∴S1=(a+b-c)2=3,∴a2+b2+c2+2ab-2ac-2bc=3,∴2c2+2ab-2ac-2bc=3,∴c2-(a+b)c+ab=1.5,∴S2=1.5.故选B.
9.C 在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,∴AB2=0.72+2.42=6.25.
在Rt△A'BD中,∵∠A'DB=90°,A'D=2米,
∴BD2+A'D2=A'B2.
又∵AB=A'B,∴BD2+22=6.25,
∵BD>0,∴BD=1.5米,
∴CD=BC+BD=0.7+1.5=2.2(米).故选C.
10.A 在Rt△BCD中,CD=AB=12,BC=5,
由勾股定理得BD==13,
由折叠可知AE=A'E,AD=BC=DA'=5,∠A=∠DA'E=90°,∴A'B=BD-DA'=8,∠BA'E=90°,
设AE=A'E=x,则BE=12-x,
在Rt△A'BE中,由勾股定理得A'E2+A'B2=BE2,
∴x2+82=(12-x)2,解得x=,
故AE的长为.
11.答案 5或
解析 ①长为3的边是直角边,长为4的边是斜边时,第三边的长为=;②长为3、4的边都是直角边时,第三边的长为=5.综上,第三边的长为5或.
12.答案 -2
解析 由勾股定理得AB==,AD==,设点E表示的数为x,则x-(-2)=,∴x=-2,即点E表示的数为-2.
13.答案 24
解析 设小正方形的边长为x,∵a=3,b=4,∴AB=3+4=7.如图,在Rt△ABC中,AC2+BC2=AB2,即(3+x)2+(x+4)2=72,整理得x2+7x-12=0,∴x2+7x=12,∴该长方形的面积=(3+x)(x+4)=x2+7x+12=12+12=24.
14.答案 (1) (2)20
解析 (1)如图,把圆柱侧面展开,连接AB,
在Rt△ADB中,∵AD=16 cm,BD=5 cm,
∴AB===(cm).
(2)如图,把圆柱侧面展开,点B与点B'关于PQ对称,连接CB',交PQ于E,连接BE,BB'过点C作CD⊥直线B'B于D,可得CD=16 cm,B'D=12 cm,
则最短路程为CB'===20(cm).
15.解析 在Rt△ABC中,AC===12.
∵∠C=90°,∠BDC=45°,∴∠DBC=45°=∠BDC,
∴CD=BC=5,∴AD=AC-CD=12-5=7.
故AD的长为7.
16.解析 在Rt△ABC中,AC=150-60=90(mm),
BC=180-60=120(mm),
∴AB===150(mm).
答:两圆孔中心A和B之间的距离为150 mm.
17.解析 (1)∵3、4、5;5、12、13;7、24、25;9、40、41;……,∴11,60,61.
(2)第一个数用字母a(a为奇数,且a≥3)表示,则用含a的代数式表示每组第二个数和第三个数分别为,.
∵a2+=,=,
∴a2+=.
又∵a为奇数,且a≥3,
∴由a,,三个数组成的数是勾股数.
18.解析 如图,连接AC,
由勾股定理可知AC===15 m.
又∵AC2+BC2=152+362=392=AB2,∴△ABC是直角三角形,∠ACB=90°.故这块地的面积=S△ABC-S△ACD=×15×36-×12×9=216(m)2.
19.解析 在Rt△ABG中,由勾股定理得AG===6(米),
∵FG=BE=1.8米,∴AF=AG+GF=6+1.8=7.8(米).
答:点A到地面的距离AF为7.8米.
20.解析 (1)如图,连接BD,
在Rt△ABD中,BD2=AB2+AD2=92+122=152,即BD=15 m,在△CBD中,CD2=172,BC2=82,而82+152=172,∴BC2+BD2=CD2,∴∠DBC=90°,
则S四边形ABCD=S△BAD+S△DBC=AD·AB+DB·BC
=×12×9+×15×8=114(m2).
答:空地ABCD的面积为114 m2.
(2)114×350=39 900(元).
答:总共需投入39 900元.
21.解析 (1)∵AC=150 m,BC=200 m,AB=250 m,
∴AC2+BC2=AB2,∴∠ACB=90°.
(2)学校C会受噪声影响.
理由:如图,过点C作CD⊥AB于点D,
∴AC·BC=CD·AB,
∴150×200=250×CD,
∴CD=120 m.
∵拖拉机周围130 m以内为受噪声影响区域,120 m<130 m,
∴学校C会受噪声影响.
(3)如图,当EC=130 m,FC=130 m时,拖拉机噪声正好影响学校,
∵ED===50(m),
∴EF=100 m.
∵拖拉机的行驶速度为每分钟50 m,
∴拖拉机噪声影响该学校持续的时间为100÷50=2(分钟).
22.解析 设点P、Q的运动时间为t s,则0≤t≤5,AP=t cm,BP=(6-t)cm,BQ=2t cm.
(1)由勾股定理,得BP2+BQ2=PQ2=(3)2=45,
即(6-t)2+(2t)2=45,解得t=3或t=-(舍去).
故3秒后,PQ的长度为3 cm.
(2)由S△PBQ=BP·BQ,得8=(6-t)·2t,
解得t=2或t=4.
故2秒或4秒后,△PBQ的面积为8 cm2.
(3)△PBQ的面积不可能是14 cm2.理由如下:
当S△PBQ=14 cm2时,BP·BQ=14,
即(6-t)·2t=14,整理得t2-6t+14=0,
∵Δ=(-6)2-4×14=-20<0,
∴方程没有实数根.
∴△PBQ的面积不可能是14 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024沪科版数学八年级下学期
第18章 勾股定理
第18章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.(2023安徽合肥瑶海期中)以下列各组数为边长,能构成直角三角形的是( )
A.1,1,2 B.2,3,4
C.4,5,6 D.1,,2
2.在下列四组数中,不是勾股数的一组数是( )
A.8,15,17 B.6,8,10
C.5,12,13 D.3,5,7
3.【新独家原创】晓波在练习本上画了四个直角三角形,并分别以这四个三角形的三边为边向外作正方形.若每个正方形中的数字及字母S分别表示所在正方形的面积,那么S的值恰好等于1的是( )
A B C D
4.(2023安徽黄山休宁期中)如图,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B恰好碰到地面,经测量AB=2米,则树高为( )
A.米 B.米
C.(+1)米 D.3米
5.(2022安徽安庆期中)直角三角形中一直角边的长为9,另两边的长为连续自然数,则直角三角形的周长为( )
A.121 B.120
C.90 D.不能确定
6.若△ABC的三边长a、b、c满足(a-b)2+|a2+b2-c2|=0,则△ABC是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
7.(2022安徽合肥五十中月考)下列说法中,错误的是( )
A.在△ABC中,若∠C=∠B=∠A,则△ABC是直角三角形
B.在△ABC中,若∠A∶∠B∶∠C=3∶4∶5,则△ABC是直角三角形
C.在△ABC中,若∠A=∠B-∠C,则△ABC是直角三角形
D.在△ABC中,若三边长a,b,c满足a∶b∶c=1∶2∶,则△ABC是直角三角形
8.(2023安徽合肥琥珀中学期中)勾股定理是我国古代伟大的数学发现之一.如图,以Rt△ABC(∠ACB=90°)的各边为边分别向外作正方形,得到三块正方形纸片,再把较小的两张正方形纸片放入最大的正方形中,重叠部分的面积记作S1,左下不重叠部分的面积记作S2,若S1=3,则S2的值是( )
A.1 B.1.5
C.2 D.2.59.如图,小巷中左、右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米 B.1.5米 C.2.2米 D.2.4米
10.【方程思想】(2022安徽合肥瑶海期中)如图,在长方形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A'处,则AE的长为( )
A. B.3 C.5 D.
二、填空题(每小题3分,共12分)
11.【分类讨论思想】(2023安徽合肥庐阳寿春中学期中)已知直角三角形的两边的长分别是3和4,则第三边长为 .
12.如图,将有一边重合的两张直角三角形纸片放在数轴上,纸片上的点A表示的数是-2,AC=BC=BD=1,若以点A为圆心、AD的长为半径画弧,与数轴交于点E(点E位于点A右侧),则点E表示的数为 .
13.【中华优秀传统文化】(2023安徽合肥五十中西校期中)我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示的长方形由两个这样的图形拼成,若a=3,b=4,则该长方形的面积为 .
14.【最短路径问题】(2023安徽合肥庐阳寿春中学期中)如图,有一个圆柱形食品盒(厚度忽略不计),它的高为10 cm,底面圆的周长为32 cm.
(1)点A位于盒外底面的边缘,如果在A处有一只蚂蚁,它想吃到盒外表面对侧中点B处的食物,则蚂蚁需要爬行的最短路程是 cm;
(2)将图1改为一个无盖的圆柱形食品盒,位于盒外的一点C距离下底面3 cm,此时蚂蚁从C处出发,爬到盒内表面对侧中点B处(如图2),则蚂蚁爬行的最短路程是 cm.
三、解答题(共58分)
15.(6分)如图,在Rt△ABC中,∠C=90°,点D是AC边上一点,∠BDC=45°,AB=13,BC=5,求AD的长.
16.(6分)一个外轮廓为长方形的机器零件平面示意图如图,根据图中标出的尺寸(单位:mm),请计算两圆孔中心A和B之间的距离.
17.【新考向·规律探究题】(6分)课堂上学习了勾股定理后,知道“勾三、股四、弦五”.王老师给出一组数让学生观察:3、4、5;5、12、13;7、24、25;9、40、41;……,学生发现这些勾股数的勾都是奇数,且从3起就没有间断过,于是王老师提出以下问题让学生解决.
(1)请你根据上述的规律写出下一组勾股数:11、 、 ;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别怎么表示 聪明的小明发现每组第二个数有这样的规律:4=,12=,24=,……,则用含a的代数式表示每组第二个数和第三个数分别为 、 ,并用所学知识加以证明.
18.【补形法】(2023安徽淮南凤台期中)(6分)如图所示的一块地,AD=12 m,CD=9 m,∠ADC=90°,AB=39 m,BC=36 m,求这块地的面积.
19.【项目式学习试题】(8分)某初中数学小组欲测量吊车起重臂顶端与地面的距离,下面是他们设计的项目课题,请你根据下面的表格求出:吊车起重臂顶端A到地面的距离AF.
项目 名称 测量吊车起重臂顶端与地面的距离
对象 简介 吊车作业时是通过液压杆CD的伸缩使起重臂AB绕点B转动的,从而使得起重臂升降作业(起重臂AB的长度也可以伸缩)
操作 示意 图
操作 数据 起重臂AB=10米,点B到地面的距离BE=1.8米,钢丝绳所在直线AF垂直地面于点F,点B到AF的距离BG=8米. 提示:四边形BEFG是长方形,BE=FG
20.【分割法】【教材变式·P60T3】(2023安徽合肥琥珀中学期中)(8分)为了绿化环境,我市某中学有一块四边形的空地ABCD,如图.学校计划在空地上种植草皮,经测量∠A=90°,AB=9 m,DA=12 m,BC=8 m,CD=17 m.
(1)求空地ABCD的面积.
(2)若每种植1平方米草皮需要350元,问总共需投入多少元
21.(8分)拖拉机行驶过程中会对周围产生较大的噪声影响.如图,有一台拖拉机沿公路AB由点A向点B行驶,AB=250 m,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为150 m和200 m,拖拉机周围130 m以内为受噪声影响区域.
(1)求∠ACB的度数.
(2)学校C会受噪声影响吗 为什么
(3)若学校受拖拉机噪声影响,拖拉机的行驶速度为每分钟50 m,则拖拉机噪声影响该学校持续的时间为多少分钟
22.(10分)如图,在Rt△ABC中,∠B=90°,AB=6 cm,BC=10 cm,点P从点A开始沿AB边向点B移动,速度为1 cm/s;点Q从点B开始沿BC边向点C移动,速度为2 cm/s,点P、Q分别从点A、B同时出发,当其中一点到达终点时,另一点也随之停止运动.
(1)几秒后,PQ的长度为3 cm
(2)几秒后,△PBQ的面积为8 cm2
(3)△PBQ的面积能不能是14 cm2 请说明理由.
第18章 勾股定理
第18章 素养综合检测
答案全解全析
1.D 12+12≠22,22+32≠42,42+52≠62,均不能构成直角三角形,故选项A、B、C不符合题意;12+()2=22,能构成直角三角形,故选项D符合题意.
2.D 82+152=172,且都是正整数,是勾股数,选项A不符合题意;62+82=102,且都是正整数,是勾股数,选项B不符合题意;52+122=132,且都是正整数,是勾股数,选项C不符合题意;32+52≠72,不是勾股数,选项D符合题意.
3.D ∵每个正方形中的数字及字母S表示所在正方形的面积,∴每个正方形中的数字以及字母S表示所在正方形的边长的平方.选项A中,由勾股定理得S=4+9=13,故选项A不符合题意;选项B中,S=9-4=5,故选项B不符合题意;选项C中,S=4+3=7,故选项C不符合题意;选项D中,S=4-3=1,故选项D符合题意.
4.C 在Rt△ACB中,根据勾股定理可求得BC==米,∴树的高度:AC+BC=(+1)米,故选C.
5.C 设另一直角边的长为a,则斜边的长为a+1.
根据勾股定理得(a+1)2-a2=92,
解得a=40,则a+1=41,
所以直角三角形的周长为9+40+41=90.
6.C ∵(a-b)2+|a2+b2-c2|=0,
∴a-b=0,a2+b2-c2=0,∴a=b,a2+b2=c2,
∴△ABC为等腰直角三角形.故选C.
7.B 在△ABC中,若∠C=∠B=∠A,则∠A+∠B+∠C=3∠C+2∠C+∠C=6∠C=180°,∴∠A=3∠C=90°,是直角三角形,选项A不符合题意;在△ABC中,若∠A∶∠B∶∠C=3∶4∶5,则最大角∠C=180°×=75°,不是直角三角形,选项B符合题意;在△ABC中,若∠A=∠B-∠C,则∠B=∠A+∠C=90°,是直角三角形,选项C不符合题意;∵12+()2=22,∴△ABC是直角三角形,选项D不符合题意.
8.B 设Rt△ABC的直角边AC=a,BC=b,BA=c,∴a2+b2=c2.∵面积为S2的长方形的长和宽分别是c-a,c-b,∴S2=(c-a)(c-b)=c2-(a+b)c+ab.∵面积为S1的正方形的边长是a+b-c,∴S1=(a+b-c)2=3,∴a2+b2+c2+2ab-2ac-2bc=3,∴2c2+2ab-2ac-2bc=3,∴c2-(a+b)c+ab=1.5,∴S2=1.5.故选B.
9.C 在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,∴AB2=0.72+2.42=6.25.
在Rt△A'BD中,∵∠A'DB=90°,A'D=2米,
∴BD2+A'D2=A'B2.
又∵AB=A'B,∴BD2+22=6.25,
∵BD>0,∴BD=1.5米,
∴CD=BC+BD=0.7+1.5=2.2(米).故选C.
10.A 在Rt△BCD中,CD=AB=12,BC=5,
由勾股定理得BD==13,
由折叠可知AE=A'E,AD=BC=DA'=5,∠A=∠DA'E=90°,∴A'B=BD-DA'=8,∠BA'E=90°,
设AE=A'E=x,则BE=12-x,
在Rt△A'BE中,由勾股定理得A'E2+A'B2=BE2,
∴x2+82=(12-x)2,解得x=,
故AE的长为.
11.答案 5或
解析 ①长为3的边是直角边,长为4的边是斜边时,第三边的长为=;②长为3、4的边都是直角边时,第三边的长为=5.综上,第三边的长为5或.
12.答案 -2
解析 由勾股定理得AB==,AD==,设点E表示的数为x,则x-(-2)=,∴x=-2,即点E表示的数为-2.
13.答案 24
解析 设小正方形的边长为x,∵a=3,b=4,∴AB=3+4=7.如图,在Rt△ABC中,AC2+BC2=AB2,即(3+x)2+(x+4)2=72,整理得x2+7x-12=0,∴x2+7x=12,∴该长方形的面积=(3+x)(x+4)=x2+7x+12=12+12=24.
14.答案 (1) (2)20
解析 (1)如图,把圆柱侧面展开,连接AB,
在Rt△ADB中,∵AD=16 cm,BD=5 cm,
∴AB===(cm).
(2)如图,把圆柱侧面展开,点B与点B'关于PQ对称,连接CB',交PQ于E,连接BE,BB'过点C作CD⊥直线B'B于D,可得CD=16 cm,B'D=12 cm,
则最短路程为CB'===20(cm).
15.解析 在Rt△ABC中,AC===12.
∵∠C=90°,∠BDC=45°,∴∠DBC=45°=∠BDC,
∴CD=BC=5,∴AD=AC-CD=12-5=7.
故AD的长为7.
16.解析 在Rt△ABC中,AC=150-60=90(mm),
BC=180-60=120(mm),
∴AB===150(mm).
答:两圆孔中心A和B之间的距离为150 mm.
17.解析 (1)∵3、4、5;5、12、13;7、24、25;9、40、41;……,∴11,60,61.
(2)第一个数用字母a(a为奇数,且a≥3)表示,则用含a的代数式表示每组第二个数和第三个数分别为,.
∵a2+=,=,
∴a2+=.
又∵a为奇数,且a≥3,
∴由a,,三个数组成的数是勾股数.
18.解析 如图,连接AC,
由勾股定理可知AC===15 m.
又∵AC2+BC2=152+362=392=AB2,∴△ABC是直角三角形,∠ACB=90°.故这块地的面积=S△ABC-S△ACD=×15×36-×12×9=216(m)2.
19.解析 在Rt△ABG中,由勾股定理得AG===6(米),
∵FG=BE=1.8米,∴AF=AG+GF=6+1.8=7.8(米).
答:点A到地面的距离AF为7.8米.
20.解析 (1)如图,连接BD,
在Rt△ABD中,BD2=AB2+AD2=92+122=152,即BD=15 m,在△CBD中,CD2=172,BC2=82,而82+152=172,∴BC2+BD2=CD2,∴∠DBC=90°,
则S四边形ABCD=S△BAD+S△DBC=AD·AB+DB·BC
=×12×9+×15×8=114(m2).
答:空地ABCD的面积为114 m2.
(2)114×350=39 900(元).
答:总共需投入39 900元.
21.解析 (1)∵AC=150 m,BC=200 m,AB=250 m,
∴AC2+BC2=AB2,∴∠ACB=90°.
(2)学校C会受噪声影响.
理由:如图,过点C作CD⊥AB于点D,
∴AC·BC=CD·AB,
∴150×200=250×CD,
∴CD=120 m.
∵拖拉机周围130 m以内为受噪声影响区域,120 m<130 m,
∴学校C会受噪声影响.
(3)如图,当EC=130 m,FC=130 m时,拖拉机噪声正好影响学校,
∵ED===50(m),
∴EF=100 m.
∵拖拉机的行驶速度为每分钟50 m,
∴拖拉机噪声影响该学校持续的时间为100÷50=2(分钟).
22.解析 设点P、Q的运动时间为t s,则0≤t≤5,AP=t cm,BP=(6-t)cm,BQ=2t cm.
(1)由勾股定理,得BP2+BQ2=PQ2=(3)2=45,
即(6-t)2+(2t)2=45,解得t=3或t=-(舍去).
故3秒后,PQ的长度为3 cm.
(2)由S△PBQ=BP·BQ,得8=(6-t)·2t,
解得t=2或t=4.
故2秒或4秒后,△PBQ的面积为8 cm2.
(3)△PBQ的面积不可能是14 cm2.理由如下:
当S△PBQ=14 cm2时,BP·BQ=14,
即(6-t)·2t=14,整理得t2-6t+14=0,
∵Δ=(-6)2-4×14=-20<0,
∴方程没有实数根.
∴△PBQ的面积不可能是14 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
