2024冀教版数学八年级下学期--专项素养综合全练(七)用转化思想求不规则图形的角度(含解析)
文档属性
| 名称 | 2024冀教版数学八年级下学期--专项素养综合全练(七)用转化思想求不规则图形的角度(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 583.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:14 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2024冀教版数学八年级下学期
专项素养综合全练(七)
用转化思想求不规则图形的角度
类型一 直接利用三角形外角性质进行转化
1.(2023山东青岛五十三中期末)如图,若∠A=31°,那么∠A+∠B+∠C+∠D+∠E=( )
A.90° B.180° C.211° D.242°
2.(2023广东中山期末)如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.90° B.180°
C.120° D.360°
3.(2023山东淄博期中)如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.180° B.260°
C.270° D.360°
4.【项目式学习试题】(2023山东青岛六十五中开学测试)利用图形这一直观性语言,在一定程度上可以降低我们认识和理解抽象逻辑推理的难度.利用图形构建几何直观,可以轻松实现空间形式和数量关系的相互转化.让我们在如下的问题解决中体验一下吧!
【模块探究】
如图1,求证:∠BOC=∠A+∠B+∠C.
【直观应用】
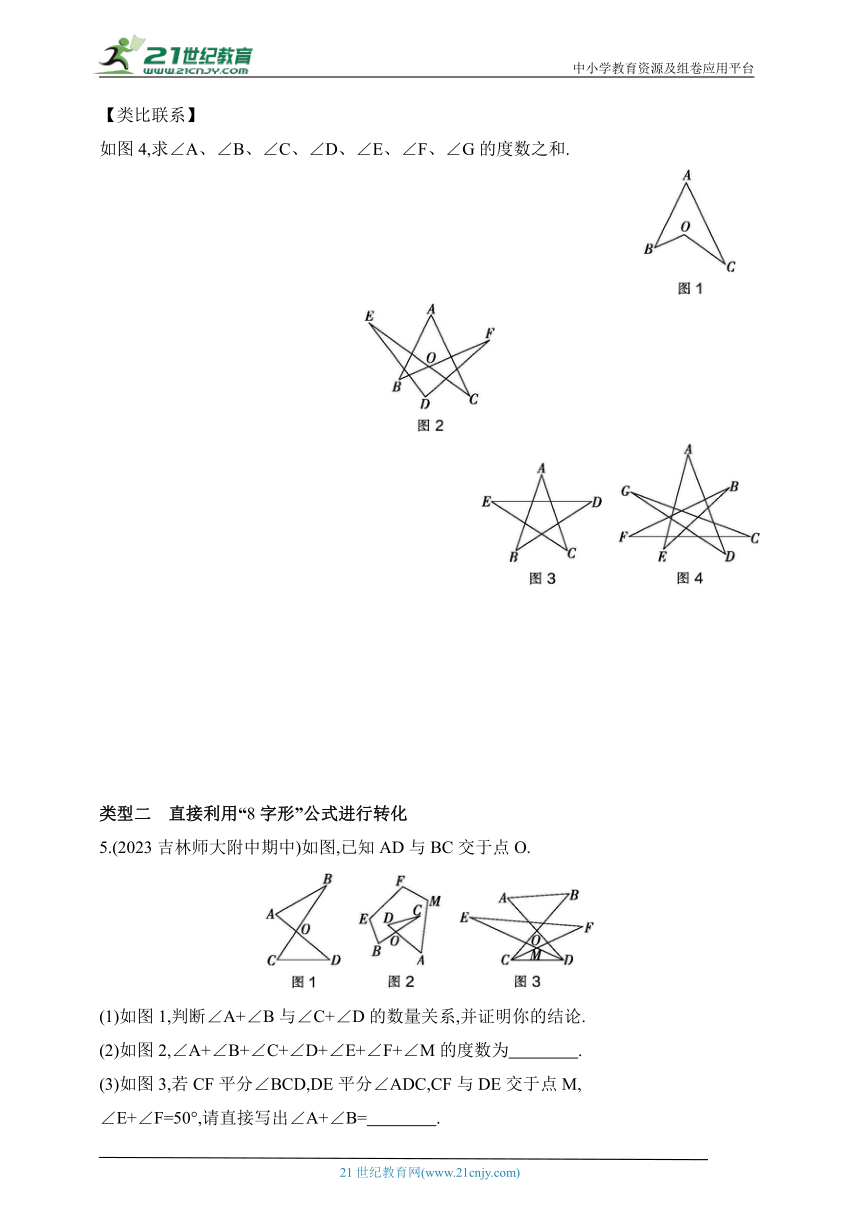
(1)如图2,∠EOF=α,则∠A、∠B、∠C、∠D、∠E、∠F的度数之和等于 .
(2)求图3中∠A、∠B、∠C、∠D、∠E的度数之和.
【类比联系】
如图4,求∠A、∠B、∠C、∠D、∠E、∠F、∠G的度数之和.
类型二 直接利用“8字形”公式进行转化
5.(2023吉林师大附中期中)如图,已知AD与BC交于点O.
(1)如图1,判断∠A+∠B与∠C+∠D的数量关系,并证明你的结论.
(2)如图2,∠A+∠B+∠C+∠D+∠E+∠F+∠M的度数为 .
(3)如图3,若CF平分∠BCD,DE平分∠ADC,CF与DE交于点M,
∠E+∠F=50°,请直接写出∠A+∠B= .
6.(2023山东青岛莱西期中)在同一平面内不重合的两条直线有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同的关系,今天我们就来探究一下这些奇妙的图形吧!
【问题探究】
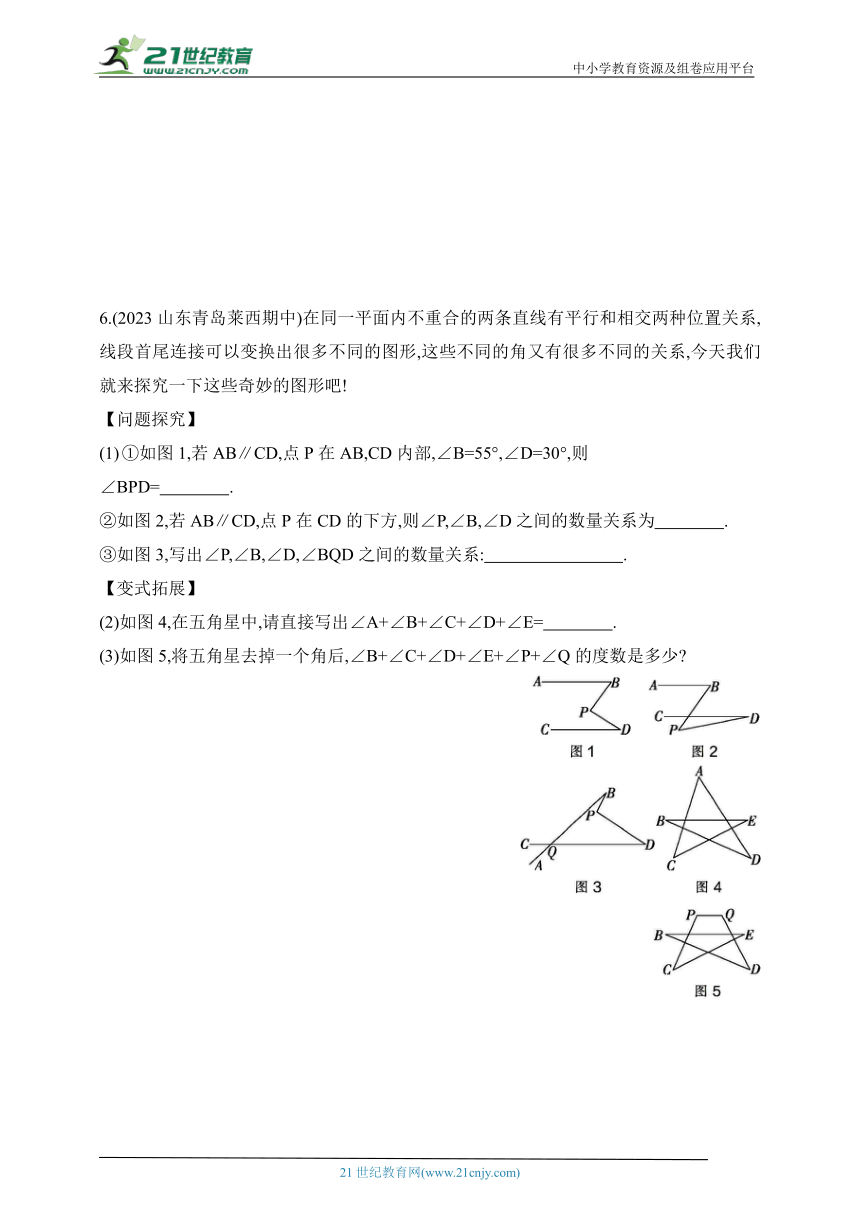
①如图1,若AB∥CD,点P在AB,CD内部,∠B=55°,∠D=30°,则
∠BPD= .
②如图2,若AB∥CD,点P在CD的下方,则∠P,∠B,∠D之间的数量关系为 .
③如图3,写出∠P,∠B,∠D,∠BQD之间的数量关系: .
【变式拓展】
(2)如图4,在五角星中,请直接写出∠A+∠B+∠C+∠D+∠E= .
(3)如图5,将五角星去掉一个角后,∠B+∠C+∠D+∠E+∠P+∠Q的度数是多少
答案全解全析
D ∵∠A=31°,∴∠AFG+∠AGF=180°-31°=149°,∵∠AFB+
∠AFG+∠AGD+∠AGF=360°,∴∠AFB+∠AGD=360°-149°=211°,
∵∠B+∠C=∠AFB,∠D+∠E=∠AGD,∴∠A+∠B+∠C+∠D+∠E=∠A+∠AFB+∠AGD=31°+211°=242°,故选D.
B 如图,∵∠1=∠2+∠C,∠2=∠A+∠D,∴∠1=∠A+∠C+∠D,
∵∠1+∠B+∠E=180°,∴∠A+∠B+∠C+∠D+∠E=180°,故选B.
3.A 如图,
∵∠1=∠B+∠2,∠2=∠D+∠E,∠A+∠1+∠C=180°,∴∠A+∠B+
∠D+∠E+∠C=180°,故选A.
4.解析 【模块探究】证明:如图1,延长BO交AC于点D,
∵∠BOC=∠C+∠CDO,∠CDO=∠A+∠B,
∴∠BOC=∠A+∠B+∠C.
【直观应用】(1)如图2,由上述结论得∠BOC=∠A+∠B+∠C,∠EOF=∠D+∠E+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠EOF=2α.故答案为2a.
如图3,BD交CE于点O,∵∠BOC=∠A+∠B+∠C,∠COD=
∠E+∠D,
∴∠A+∠B+∠C+∠E+∠D=∠BOC+∠COD=180°.
【类比联系】如图4,GD与EB交于点M,GC与EB交于点N.
∵∠DMN=∠G+∠GNM,∠GNM=∠BNC=∠F+∠B+∠C,
∴∠DMN=∠G+∠F+∠B+∠C,
∵∠EMD=∠A+∠E+∠D,
∴∠A+∠E+∠D+∠G+∠F+∠B+∠C=∠EMD+∠DMN=180°.
5.解析 (1)∠A+∠B=∠C+∠D.
证明:∵∠AOB+∠A+∠B=180°=∠COD+∠C+∠D,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)如图,连接AB,
由(1)得,∠OBA+∠OAB=∠C+∠D,
∴∠DAM+∠CBE+∠C+∠D+∠E+∠F+∠M的度数为五边形ABEFM的内角和,即(5-2)×180°=540°,
故答案为540°.
(3)∵CF平分∠BCD,DE平分∠ADC,
∴∠MCD=∠OCD,∠MDC=∠ODC,
由(1)可得,∠E+∠F=∠MCD+∠MDC,
∴∠OCD+∠ODC=50°,
∴∠OCD+∠ODC=100°,
∴∠A+∠B=∠OCD+∠ODC=100°.
故答案为100°.
6.解析 (1)①如图1,过点P作PQ∥AB,
∵AB∥CD,∴AB∥PQ∥CD,
∴∠B=∠BPQ,∠D=∠DPQ,∴∠BPD=∠BPQ+∠DPQ=∠B+
∠D=55°+30°=85°.
故答案为85°.
②如图2,CD与BP交于点Q,
∵AB∥CD,∴∠B=∠BQD,
又∵∠BQD=∠D+∠P,∴∠B=∠P+∠D.
故答案为∠B=∠P+∠D.
③如图3,延长BP交CD于点E,
∵∠BPD=∠D+∠BED,∠BED=∠QBP+∠BQD,
∴∠BPD=∠D+∠QBP+∠BQD,
故答案为∠P=∠BQD+∠B+∠D.
(2)如图4,连接CD,
易知∠B+∠E=∠ECD+∠BDC,
∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠ECD+∠BDC+∠ACE+
∠ADB=∠A+∠ACD+∠ADC=180°.
故答案为180°.
(3)如图5,连接CD,
易知∠B+∠E=∠DCE+∠BDC,
∵∠PCE+∠DCE+∠BDC+∠BDQ+∠P+∠Q=360°,
∴∠B+∠PCE+∠BDQ+∠E+∠P+∠Q=360°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024冀教版数学八年级下学期
专项素养综合全练(七)
用转化思想求不规则图形的角度
类型一 直接利用三角形外角性质进行转化
1.(2023山东青岛五十三中期末)如图,若∠A=31°,那么∠A+∠B+∠C+∠D+∠E=( )
A.90° B.180° C.211° D.242°
2.(2023广东中山期末)如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.90° B.180°
C.120° D.360°
3.(2023山东淄博期中)如图,∠A+∠B+∠C+∠D+∠E的度数为( )
A.180° B.260°
C.270° D.360°
4.【项目式学习试题】(2023山东青岛六十五中开学测试)利用图形这一直观性语言,在一定程度上可以降低我们认识和理解抽象逻辑推理的难度.利用图形构建几何直观,可以轻松实现空间形式和数量关系的相互转化.让我们在如下的问题解决中体验一下吧!
【模块探究】
如图1,求证:∠BOC=∠A+∠B+∠C.
【直观应用】
(1)如图2,∠EOF=α,则∠A、∠B、∠C、∠D、∠E、∠F的度数之和等于 .
(2)求图3中∠A、∠B、∠C、∠D、∠E的度数之和.
【类比联系】
如图4,求∠A、∠B、∠C、∠D、∠E、∠F、∠G的度数之和.
类型二 直接利用“8字形”公式进行转化
5.(2023吉林师大附中期中)如图,已知AD与BC交于点O.
(1)如图1,判断∠A+∠B与∠C+∠D的数量关系,并证明你的结论.
(2)如图2,∠A+∠B+∠C+∠D+∠E+∠F+∠M的度数为 .
(3)如图3,若CF平分∠BCD,DE平分∠ADC,CF与DE交于点M,
∠E+∠F=50°,请直接写出∠A+∠B= .
6.(2023山东青岛莱西期中)在同一平面内不重合的两条直线有平行和相交两种位置关系,线段首尾连接可以变换出很多不同的图形,这些不同的角又有很多不同的关系,今天我们就来探究一下这些奇妙的图形吧!
【问题探究】
①如图1,若AB∥CD,点P在AB,CD内部,∠B=55°,∠D=30°,则
∠BPD= .
②如图2,若AB∥CD,点P在CD的下方,则∠P,∠B,∠D之间的数量关系为 .
③如图3,写出∠P,∠B,∠D,∠BQD之间的数量关系: .
【变式拓展】
(2)如图4,在五角星中,请直接写出∠A+∠B+∠C+∠D+∠E= .
(3)如图5,将五角星去掉一个角后,∠B+∠C+∠D+∠E+∠P+∠Q的度数是多少
答案全解全析
D ∵∠A=31°,∴∠AFG+∠AGF=180°-31°=149°,∵∠AFB+
∠AFG+∠AGD+∠AGF=360°,∴∠AFB+∠AGD=360°-149°=211°,
∵∠B+∠C=∠AFB,∠D+∠E=∠AGD,∴∠A+∠B+∠C+∠D+∠E=∠A+∠AFB+∠AGD=31°+211°=242°,故选D.
B 如图,∵∠1=∠2+∠C,∠2=∠A+∠D,∴∠1=∠A+∠C+∠D,
∵∠1+∠B+∠E=180°,∴∠A+∠B+∠C+∠D+∠E=180°,故选B.
3.A 如图,
∵∠1=∠B+∠2,∠2=∠D+∠E,∠A+∠1+∠C=180°,∴∠A+∠B+
∠D+∠E+∠C=180°,故选A.
4.解析 【模块探究】证明:如图1,延长BO交AC于点D,
∵∠BOC=∠C+∠CDO,∠CDO=∠A+∠B,
∴∠BOC=∠A+∠B+∠C.
【直观应用】(1)如图2,由上述结论得∠BOC=∠A+∠B+∠C,∠EOF=∠D+∠E+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠EOF=2α.故答案为2a.
如图3,BD交CE于点O,∵∠BOC=∠A+∠B+∠C,∠COD=
∠E+∠D,
∴∠A+∠B+∠C+∠E+∠D=∠BOC+∠COD=180°.
【类比联系】如图4,GD与EB交于点M,GC与EB交于点N.
∵∠DMN=∠G+∠GNM,∠GNM=∠BNC=∠F+∠B+∠C,
∴∠DMN=∠G+∠F+∠B+∠C,
∵∠EMD=∠A+∠E+∠D,
∴∠A+∠E+∠D+∠G+∠F+∠B+∠C=∠EMD+∠DMN=180°.
5.解析 (1)∠A+∠B=∠C+∠D.
证明:∵∠AOB+∠A+∠B=180°=∠COD+∠C+∠D,∠AOB=∠COD,
∴∠A+∠B=∠C+∠D.
(2)如图,连接AB,
由(1)得,∠OBA+∠OAB=∠C+∠D,
∴∠DAM+∠CBE+∠C+∠D+∠E+∠F+∠M的度数为五边形ABEFM的内角和,即(5-2)×180°=540°,
故答案为540°.
(3)∵CF平分∠BCD,DE平分∠ADC,
∴∠MCD=∠OCD,∠MDC=∠ODC,
由(1)可得,∠E+∠F=∠MCD+∠MDC,
∴∠OCD+∠ODC=50°,
∴∠OCD+∠ODC=100°,
∴∠A+∠B=∠OCD+∠ODC=100°.
故答案为100°.
6.解析 (1)①如图1,过点P作PQ∥AB,
∵AB∥CD,∴AB∥PQ∥CD,
∴∠B=∠BPQ,∠D=∠DPQ,∴∠BPD=∠BPQ+∠DPQ=∠B+
∠D=55°+30°=85°.
故答案为85°.
②如图2,CD与BP交于点Q,
∵AB∥CD,∴∠B=∠BQD,
又∵∠BQD=∠D+∠P,∴∠B=∠P+∠D.
故答案为∠B=∠P+∠D.
③如图3,延长BP交CD于点E,
∵∠BPD=∠D+∠BED,∠BED=∠QBP+∠BQD,
∴∠BPD=∠D+∠QBP+∠BQD,
故答案为∠P=∠BQD+∠B+∠D.
(2)如图4,连接CD,
易知∠B+∠E=∠ECD+∠BDC,
∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠ECD+∠BDC+∠ACE+
∠ADB=∠A+∠ACD+∠ADC=180°.
故答案为180°.
(3)如图5,连接CD,
易知∠B+∠E=∠DCE+∠BDC,
∵∠PCE+∠DCE+∠BDC+∠BDQ+∠P+∠Q=360°,
∴∠B+∠PCE+∠BDQ+∠E+∠P+∠Q=360°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
