2024青岛版数学八年级下学期--专项素养综合全练(一)平行四边形及特殊平行四边形中的四种常考模型(含解析)
文档属性
| 名称 | 2024青岛版数学八年级下学期--专项素养综合全练(一)平行四边形及特殊平行四边形中的四种常考模型(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 371.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览

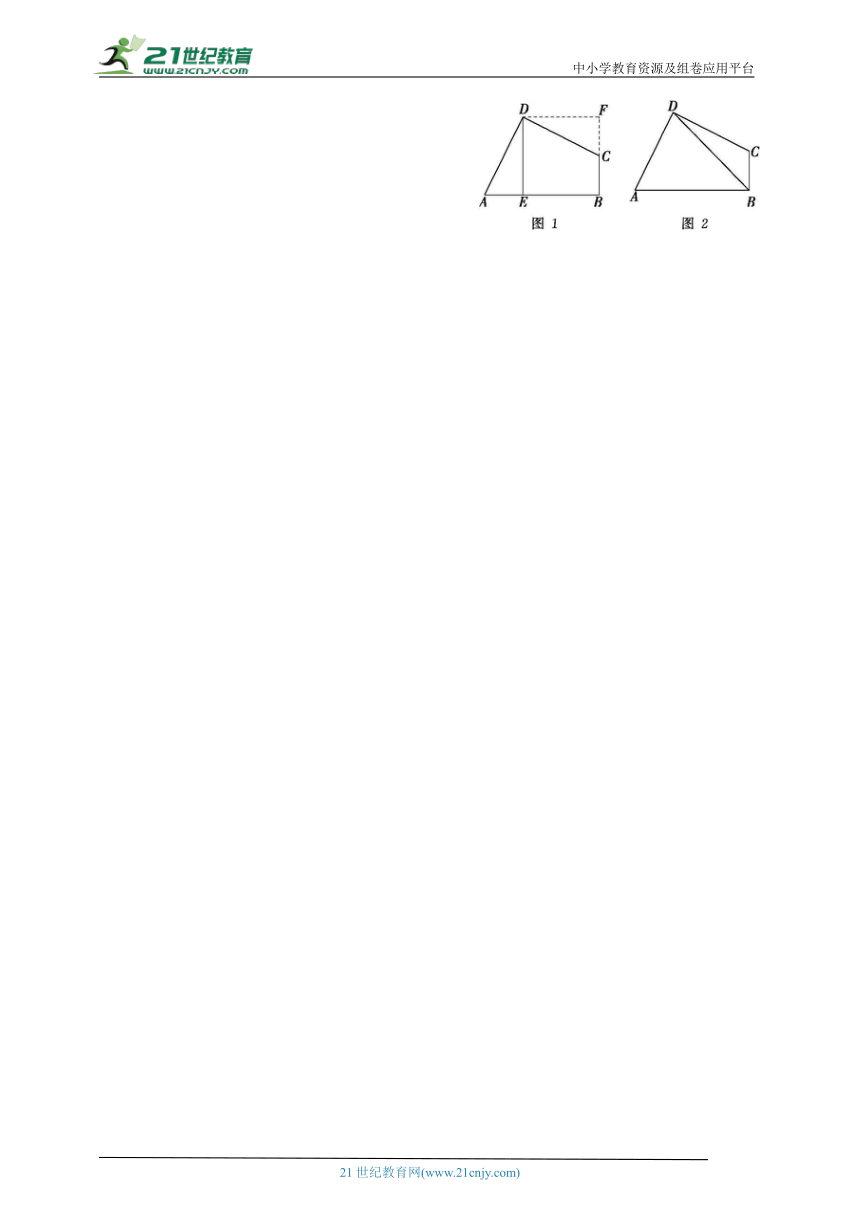

文档简介
中小学教育资源及组卷应用平台
2024青岛版数学八年级下学期
专项素养综合全练(一)
平行四边形及特殊平行四边形
中的四种常考模型
模型一 “半角”全等模型
1.【教材变式·P29T14】如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE、AF、EF,∠EAF=45°.
(1)求证:DF+BE=EF.
(2)过点A作AH⊥EF,垂足为H,求证:AH=AD.
模型二 “十字架”模型
2.【教材变式·P37T16】【问题】如图,四边形ABCD是一个正方形花园,E、F是它的两个门,且DE=CF,要修建两条路BE和AF,请证明BE=AF,BE⊥AF.
【探究】去掉“DE=CF”这一条件.
(1)若已知BE=AF,则BE⊥AF吗 请说明理由.
(2)若已知BE⊥AF,则BE=AF吗 请说明理由.
模型三 对角互补模型
3.(2022吉林长春期末)
(1)如图1,四边形ABCD中,∠ADC=∠B=90°,DE⊥AB,垂足为E,且AD=CD,DE=5,求四边形ABCD的面积.可作如下思考:过点D作DF⊥BC,交BC的延长线于点F,则有△ADE≌△CDF,由此可证DE=DF,进一步得出四边形DEBF的形状为 ,最后得出四边形ABCD的面积为 .
(2)如图2,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,BD=6,求四边形ABCD的面积.
模型四 含60°角的菱形
4.如图,在菱形ABCD中,∠A=60°,点E、F分别为AD、DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( )
A.逐渐增加
B.逐渐减小
C.始终与EF的长度相等
D.保持不变且与AB的长度相等
5.【新独家原创】如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,AE=BF,
(1)若EF=2,求△DEF的周长.
(2)若菱形ABCD的面积为8,求四边形DEBF的面积.
答案全解全析
1.证明 (1)如图,延长CB至点G,使BG=DF,连接AG.
因为四边形ABCD是正方形,所以AD=AB,∠D=∠ABE=90°,
所以∠ABG=90°.在△ABG和△ADF中,,
所以△ABG≌△ADF(SAS),所以AG=AF,∠GAB=∠DAF.
因为∠EAF=45°,所以∠GAE=∠BAE+∠GAB=∠BAE+∠DAF=45°,所以∠EAF=∠GAE.在△AEG和△AEF中,
所以△AEG≌△AEF(SAS),所以GE=EF,
所以DF+BE=BG+BE=GE=EF.
(2)补全图形后,如图,由(1)得△AEG≌△AEF,
所以EG=EF,S△AEG=S△AEF,所以GE·AB=EF·AH,所以AB=AH,
因为AB=AD,所以AH=AD.
方法解读 当一个小角度数等于与其共顶点的大角度数一半时,可考虑“半角”全等模型.对于“半角”全等模型,一般情况下需要作辅助线(构造等角或旋转一定角度),构造全等三角形,利用全等三角形的性质得到相关结论.
2.解析 【问题】证明:因为四边形ABCD是正方形,
所以∠BAE=∠D=90°,AB=AD=CD,因为DE=CF,所以AE=DF,
所以△BAE≌△ADF,所以BE=AF,∠ABE=∠FAD.
因为∠ABE+∠AEB=90°,所以∠FAD+∠AEB=90°,
所以∠AOE=90°,所以BE⊥AF.
【探究】(1)BE⊥AF,理由如下:
因为四边形ABCD是正方形,所以∠BAE=∠D=90°,AB=AD,
因为BE=AF,所以Rt△BAE≌Rt△ADF(HL),所以∠ABE=∠FAD.
因为∠ABE+∠AEB=90°,所以∠FAD+∠AEB=90°,
所以∠AOE=90°,所以BE⊥AF.
(2)BE=AF,理由如下:
因为四边形ABCD是正方形,所以∠BAE=∠D=90°,AB=AD,
因为BE⊥AF,所以∠AOE=90°,所以∠FAD+∠AEB=90°,
因为∠ABE+∠AEB=90°,所以∠ABE=∠FAD,
所以△BAE≌△ADF(ASA),所以BE=AF.
3.解析 (1)由题可知,∠F=∠B=∠DEB=90°,
所以四边形DEBF是矩形,所以∠EDF=90°.
因为∠ADC=90°,所以∠ADC=∠EDF,所以∠ADE=∠CDF,
因为∠AED=∠F,AD=CD,所以△ADE≌△CDF(AAS),所以DE=DF,
所以四边形DEBF是正方形,所以四边形ABCD的面积等于正方形DEBF的面积,所以四边形ABCD的面积为52=25.故填正方形;25.
(2)如图,过点D作DF⊥BD,交BC的延长线于F,则∠BDF=90°,所以∠BDF=∠ADC,所以∠ADB=∠CDF.因为∠ADC=∠ABC=90°,所以∠A+∠BCD=180°,因为∠BCD+∠DCF=180°,所以∠A=∠DCF,又因为AD=CD,所以△ADB≌△CDF(ASA),所以BD=DF=6,S△ADB=S△CDF,所以S四边形ABCD=S△BDF.因为BD=DF=6,∠BDF=90°,
所以S△BDF=×6×6=18,
所以S四边形ABCD=18,即四边形ABCD的面积为18.
4.D 如图,连接BD,因为四边形ABCD是菱形,
所以AB=AD=CD,AB∥CD,因为∠A=60°,所以△ABD是等边三角形,所以AB=BD,∠ABD=60°.因为DC∥AB,所以∠CDB=∠ABD=60°,
所以∠A=∠CDB,因为∠ABD=∠EBF=60°,
所以∠ABE+∠EBD=∠EBD+∠DBF,即∠ABE=∠DBF.
在△ABE和△DBF中,
所以△ABE≌△DBF(ASA),
所以AE=DF,所以AE+CF=DF+CF=CD=AB,故选D.
5.解析 (1)如图,连接BD,因为四边形ABCD是菱形,
所以AB=BC=CD,∠C=∠A=60°,AD∥BC,所以△BCD是等边三角形,∠ABC=180°-∠A=120°,所以∠BDC=∠DBC=60°,BD=CD,
所以∠DBE=∠ABC-∠DBC=60°,所以∠DBE=∠C.
因为AE=BF,所以AB-AE=BC-BF,即BE=CF.
在△DBE和△DCF中,所以△DBE≌△DCF(SAS),
所以DE=DF,∠EDB=∠FDC,
所以∠EDB+∠BDF=∠FDC+∠BDF=∠BDC=60°,所以∠EDF=60°,
所以△DEF是等边三角形,所以DE=DF=EF=2,
所以△DEF的周长为2×3=6.
(2)由(1)得△DBE≌△DCF,所以S△DBE=S△DCF,
所以S四边形DEBF=S△DBE+S△DBF=S△DCF+S△DBF=S△DBC.
因为S菱形ABCD=2S△DBC=8,所以S△DBC=4,
所以S四边形DEBF=4,即四边形DEBF的面积为4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学八年级下学期
专项素养综合全练(一)
平行四边形及特殊平行四边形
中的四种常考模型
模型一 “半角”全等模型
1.【教材变式·P29T14】如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE、AF、EF,∠EAF=45°.
(1)求证:DF+BE=EF.
(2)过点A作AH⊥EF,垂足为H,求证:AH=AD.
模型二 “十字架”模型
2.【教材变式·P37T16】【问题】如图,四边形ABCD是一个正方形花园,E、F是它的两个门,且DE=CF,要修建两条路BE和AF,请证明BE=AF,BE⊥AF.
【探究】去掉“DE=CF”这一条件.
(1)若已知BE=AF,则BE⊥AF吗 请说明理由.
(2)若已知BE⊥AF,则BE=AF吗 请说明理由.
模型三 对角互补模型
3.(2022吉林长春期末)
(1)如图1,四边形ABCD中,∠ADC=∠B=90°,DE⊥AB,垂足为E,且AD=CD,DE=5,求四边形ABCD的面积.可作如下思考:过点D作DF⊥BC,交BC的延长线于点F,则有△ADE≌△CDF,由此可证DE=DF,进一步得出四边形DEBF的形状为 ,最后得出四边形ABCD的面积为 .
(2)如图2,四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,BD=6,求四边形ABCD的面积.
模型四 含60°角的菱形
4.如图,在菱形ABCD中,∠A=60°,点E、F分别为AD、DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( )
A.逐渐增加
B.逐渐减小
C.始终与EF的长度相等
D.保持不变且与AB的长度相等
5.【新独家原创】如图,在菱形ABCD中,∠A=60°,点E,F分别在边AB,BC上,AE=BF,
(1)若EF=2,求△DEF的周长.
(2)若菱形ABCD的面积为8,求四边形DEBF的面积.
答案全解全析
1.证明 (1)如图,延长CB至点G,使BG=DF,连接AG.
因为四边形ABCD是正方形,所以AD=AB,∠D=∠ABE=90°,
所以∠ABG=90°.在△ABG和△ADF中,,
所以△ABG≌△ADF(SAS),所以AG=AF,∠GAB=∠DAF.
因为∠EAF=45°,所以∠GAE=∠BAE+∠GAB=∠BAE+∠DAF=45°,所以∠EAF=∠GAE.在△AEG和△AEF中,
所以△AEG≌△AEF(SAS),所以GE=EF,
所以DF+BE=BG+BE=GE=EF.
(2)补全图形后,如图,由(1)得△AEG≌△AEF,
所以EG=EF,S△AEG=S△AEF,所以GE·AB=EF·AH,所以AB=AH,
因为AB=AD,所以AH=AD.
方法解读 当一个小角度数等于与其共顶点的大角度数一半时,可考虑“半角”全等模型.对于“半角”全等模型,一般情况下需要作辅助线(构造等角或旋转一定角度),构造全等三角形,利用全等三角形的性质得到相关结论.
2.解析 【问题】证明:因为四边形ABCD是正方形,
所以∠BAE=∠D=90°,AB=AD=CD,因为DE=CF,所以AE=DF,
所以△BAE≌△ADF,所以BE=AF,∠ABE=∠FAD.
因为∠ABE+∠AEB=90°,所以∠FAD+∠AEB=90°,
所以∠AOE=90°,所以BE⊥AF.
【探究】(1)BE⊥AF,理由如下:
因为四边形ABCD是正方形,所以∠BAE=∠D=90°,AB=AD,
因为BE=AF,所以Rt△BAE≌Rt△ADF(HL),所以∠ABE=∠FAD.
因为∠ABE+∠AEB=90°,所以∠FAD+∠AEB=90°,
所以∠AOE=90°,所以BE⊥AF.
(2)BE=AF,理由如下:
因为四边形ABCD是正方形,所以∠BAE=∠D=90°,AB=AD,
因为BE⊥AF,所以∠AOE=90°,所以∠FAD+∠AEB=90°,
因为∠ABE+∠AEB=90°,所以∠ABE=∠FAD,
所以△BAE≌△ADF(ASA),所以BE=AF.
3.解析 (1)由题可知,∠F=∠B=∠DEB=90°,
所以四边形DEBF是矩形,所以∠EDF=90°.
因为∠ADC=90°,所以∠ADC=∠EDF,所以∠ADE=∠CDF,
因为∠AED=∠F,AD=CD,所以△ADE≌△CDF(AAS),所以DE=DF,
所以四边形DEBF是正方形,所以四边形ABCD的面积等于正方形DEBF的面积,所以四边形ABCD的面积为52=25.故填正方形;25.
(2)如图,过点D作DF⊥BD,交BC的延长线于F,则∠BDF=90°,所以∠BDF=∠ADC,所以∠ADB=∠CDF.因为∠ADC=∠ABC=90°,所以∠A+∠BCD=180°,因为∠BCD+∠DCF=180°,所以∠A=∠DCF,又因为AD=CD,所以△ADB≌△CDF(ASA),所以BD=DF=6,S△ADB=S△CDF,所以S四边形ABCD=S△BDF.因为BD=DF=6,∠BDF=90°,
所以S△BDF=×6×6=18,
所以S四边形ABCD=18,即四边形ABCD的面积为18.
4.D 如图,连接BD,因为四边形ABCD是菱形,
所以AB=AD=CD,AB∥CD,因为∠A=60°,所以△ABD是等边三角形,所以AB=BD,∠ABD=60°.因为DC∥AB,所以∠CDB=∠ABD=60°,
所以∠A=∠CDB,因为∠ABD=∠EBF=60°,
所以∠ABE+∠EBD=∠EBD+∠DBF,即∠ABE=∠DBF.
在△ABE和△DBF中,
所以△ABE≌△DBF(ASA),
所以AE=DF,所以AE+CF=DF+CF=CD=AB,故选D.
5.解析 (1)如图,连接BD,因为四边形ABCD是菱形,
所以AB=BC=CD,∠C=∠A=60°,AD∥BC,所以△BCD是等边三角形,∠ABC=180°-∠A=120°,所以∠BDC=∠DBC=60°,BD=CD,
所以∠DBE=∠ABC-∠DBC=60°,所以∠DBE=∠C.
因为AE=BF,所以AB-AE=BC-BF,即BE=CF.
在△DBE和△DCF中,所以△DBE≌△DCF(SAS),
所以DE=DF,∠EDB=∠FDC,
所以∠EDB+∠BDF=∠FDC+∠BDF=∠BDC=60°,所以∠EDF=60°,
所以△DEF是等边三角形,所以DE=DF=EF=2,
所以△DEF的周长为2×3=6.
(2)由(1)得△DBE≌△DCF,所以S△DBE=S△DCF,
所以S四边形DEBF=S△DBE+S△DBF=S△DCF+S△DBF=S△DBC.
因为S菱形ABCD=2S△DBC=8,所以S△DBC=4,
所以S四边形DEBF=4,即四边形DEBF的面积为4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
