2024青岛版数学八年级下学期--第6章《平行四边形》素养综合检测(含解析)
文档属性
| 名称 | 2024青岛版数学八年级下学期--第6章《平行四边形》素养综合检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 509.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024青岛版数学八年级下学期
第6章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共36分)
1.(2023四川成都中考)如图,在 ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是 ( )
A.AC=BD B.OA=OC
C.AC⊥BD D.∠ADC=∠BCD
2.(2022山东滨州中考)下列命题,其中是真命题的是 ( )
A.对角线互相垂直的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形
D.对角线互相垂直的矩形是正方形
3.如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,连接DE,EF,DF,则图中平行四边形的个数是 ( )
A.2 B.3
C.4 D.5
4.(2023北京清华附中期中)如图,在 ABCD中,AE⊥CD于点E,∠B=60°,则∠DAE等于( )
A.15° B.30° C.45° D.60°
5.【平行线+角平分线】(2023山东聊城东阿、临清期中)如图,在 ABCD中,AD=2AB,CE平分∠BCD,交AD边于点E,且AE=5,则AB的长为( )
A. B.3 C.4 D.5
6.【新考向·尺规作图】(2023湖北随州中考)如图,在 ABCD中,分别以B,D为圆心,大于BD的长为半径画弧,两弧相交于点M,N,过M,N两点作直线交BD于点O,交AD,BC于点E,F,下列结论不正确的是( )
A.AE=CF B.DE=BF C.OE=OF D.DE=DC
7.(2023四川泸州中考)如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( )
A.1 B.2 C.3 D.4
8.(2023山东菏泽曹县期中)如图,在菱形ABCD中,对角线AC,BD交于点O,DE⊥AB于点E,连接OE,若∠DAB=70°,则∠EOB的度数是( )
A.50° B.60° C.70° D.80°
9.(2022山东聊城东阿期中)若顺次连接四边形ABCD各边中点所得到的四边形是矩形,则四边形ABCD必然是( )
A.菱形
B.对角线互相垂直的四边形
C.正方形
D.对角线相等的四边形
10.【分类讨论思想】(2022山东聊城临清期中)如图,在四边形ABCD中,AD∥BC,AD=8 cm,BC=12 cm,M是BC上一点,且BM=9 cm,点E从点A出发,以1 cm/s的速度向点D运动,点F从点C出发,以3 cm/s的速度向点B运动,当其中一点到达终点时,另一点也随之停止,设运动时间为t(s),当以A、M、E、F为顶点的四边形是平行四边形时,t的值是( )
A. B.3 C.3或 D.或
11.【“半角”全等模型】(2023重庆中考A卷)如图,在正方形 ABCD中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于( )
A.2α B.90°-2α
C.45°-α D.90°-α
12.(2022山东东营垦利期末)如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD的延长线上一点,且CD=DE,连接BE,分别交AC、AD于点F、G,连接OG,下列结论:①OG=AB;②S四边形ODGF>S△ABF;③以点A、B、D、E为顶点的四边形是菱形;④S△ACD=4S△BOG.其中正确的是( )
A.①② B.①②③
C.①③④ D.②③④
二、填空题(每小题3分,共15分)
13.【新考法】(2022湖北荆州中考)如图,点E,F分别在 ABCD的边AB,CD的延长线上,连接EF,分别交AD,BC于G,H.添加一个条件使△AEG≌△CFH,这个条件可以是 .(只需写一种情况)
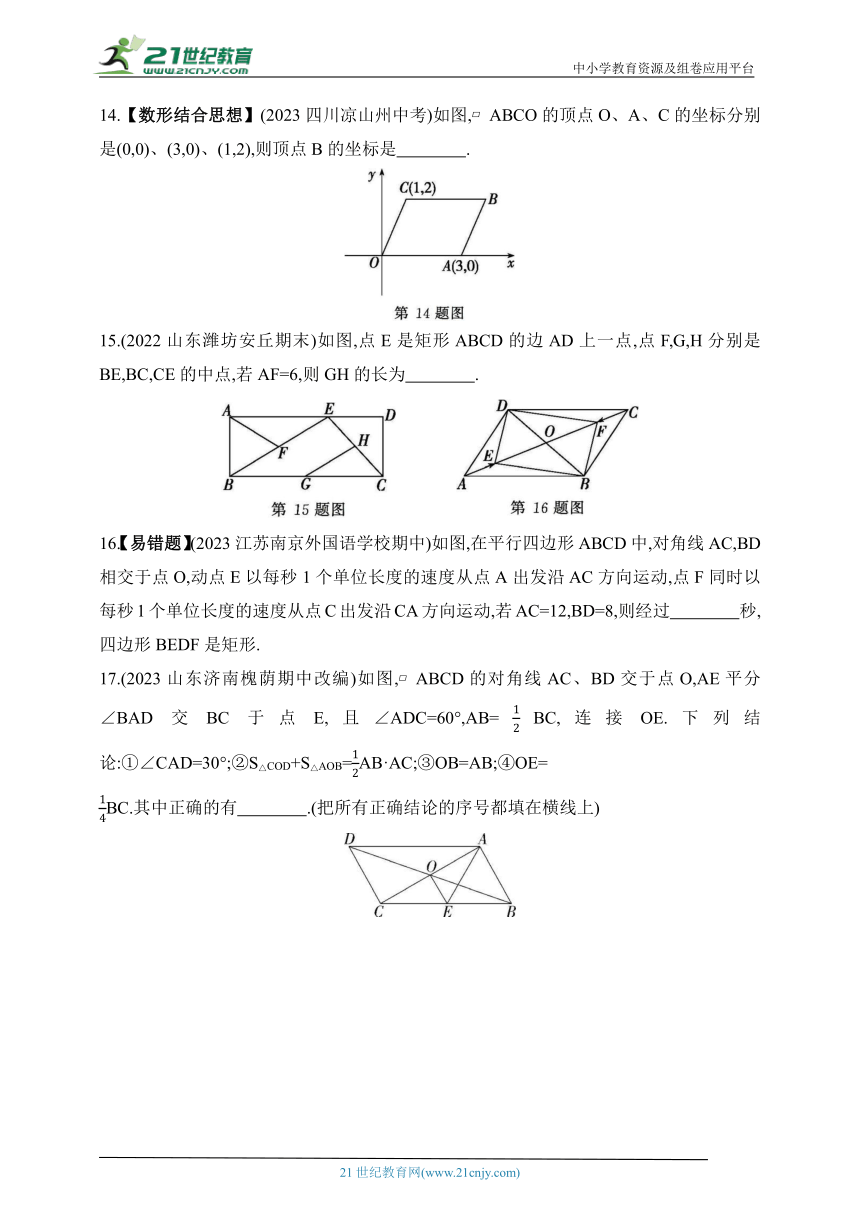
14.【数形结合思想】(2023四川凉山州中考)如图, ABCO的顶点O、A、C的坐标分别是(0,0)、(3,0)、(1,2),则顶点B的坐标是 .
15.(2022山东潍坊安丘期末)如图,点E是矩形ABCD的边AD上一点,点F,G,H分别是BE,BC,CE的中点,若AF=6,则GH的长为 .
16.【易错题】(2023江苏南京外国语学校期中)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,动点E以每秒1个单位长度的速度从点A出发沿AC方向运动,点F同时以每秒1个单位长度的速度从点C出发沿CA方向运动,若AC=12,BD=8,则经过 秒,四边形BEDF是矩形.
17.(2023山东济南槐荫期中改编)如图, ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S△COD+S△AOB=AB·AC;③OB=AB;④OE=
BC.其中正确的有 .(把所有正确结论的序号都填在横线上)
三、解答题(共49分)
18.(2022江苏常州期中)(12分)如图,四边形ABCD是平行四边形,AE,CF分别平分∠BAD和∠BCD,交BD于点E,F.
(1)若∠BCF=65°,求∠ABC的度数.
(2)连接CE,AF,求证:四边形AECF是平行四边形.
19.【教材变式·P28T7】(2023湖北随州中考改编)(12分)如图,矩形ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.
(1)求证:CE=DE.
(2)若BC=3,DC=2,求四边形OCED的面积.
20.【教材变式·P26例2】(2023浙江绍兴中考)(12分)如图,在正方形ABCD中,G是对角线BD上的一点(与点B,D不重合),GE⊥CD,GF⊥
BC,E,F分别为垂足.连接EF,AG,并延长AG交EF于点H.
(1)求证:∠DAG=∠EGH.
(2)判断AH与EF是否垂直,并说明理由.
21.(13分)如图,在 ABCD中,对角线AC与BD相交于点O,点M,N分别为OB,OD的中点,连接AM并延长至点E,使EM=AM,连接CE,CN.
(1)求证:△ABM≌△CDN.
(2)当AB与AC满足什么数量关系时,四边形MECN是矩形 请说明理由.
(3)连接AN,EN,当△ANE满足什么条件时,四边形MECN是正方形 请说明理由.
答案全解全析
一、选择题
1.B 平行四边形的对角线互相平分,但不一定相等,不一定垂直,选项B正确,选项A,C不一定正确.平行四边形的对角相等,但邻角不一定相等,选项D不一定正确.
2.D
3.B ∵D,E,F分别是AB,BC,CA的中点,
∴DE,DF,EF是△ABC的中位线,
∴DE∥AC,DF∥BC,EF∥AB,
∴四边形EDFC、四边形EBDF、四边形ADEF均是平行四边形.
故选B.
4.B 因为四边形ABCD是平行四边形,所以∠D=∠B=60°,
因为AE⊥CD,所以∠AED=90°,所以∠DAE=90°-∠D=30°.故选B.
5.D 因为四边形ABCD为平行四边形,所以AB=CD,AD∥BC,所以∠DEC=∠ECB,因为CE平分∠BCD,所以∠DCE=∠ECB,所以∠DEC=∠DCE,所以CD=DE.因为AD=2AB,所以AD=2CD=2ED,因为AD=AE+ED,所以ED=AE=5,所以AB=5.故选D.
6.D 根据作图可知,EF垂直平分BD,所以BO=DO.因为四边形ABCD是平行四边形,所以AD=BC,AD∥BC,所以∠EDO=∠FBO,因为∠BOF=∠DOE,所以△BOF≌△DOE(ASA),所以BF=DE,OE=OF,选项B,C正确.因为AD-DE=BC-BF,所以AE=CF,选项A正确.无法证明DE=CD,选项D错误.故选D.
7.A 因为四边形ABCD为平行四边形,所以AB∥DC,AB=CD=6,OD=OB,所以∠CDP=∠APD.因为DP平分∠ADC,所以∠CDP=∠ADP,所以∠ADP=∠APD,所以AP=AD=4,所以PB=AB-AP=6-4=2.因为E是PD的中点,O是BD的中点,所以EO是△DPB的中位线,所以EO=PB=1,故选A.
8.C 因为四边形ABCD是菱形,所以AB=AD,DO=BO.因为∠DAB=70°,所以∠ABD=∠ADB==55°.因为DE⊥AB,所以∠DEB=90°.在Rt△DEB中,因为DO=BO,所以OE=BO=DO=DB,所以∠OEB=∠ABD=55°,所以∠EOB=180°-55°-55°=70°.
9.B 如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、AD的中点,所以EH∥FG∥BD,EF∥AC∥HG,因为四边形EFGH是矩形,所以EF⊥FG,所以AC⊥BD,故选B.
10.D 因为AD∥BC,所以①当F在线段CM上,且AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,则t=12-9-3t,解得t=;②当点F在线段BM上,且AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,则t=3t-(12-9),解得t=.综上所述,当t=或时,以A、M、E、F为顶点的四边形是平行四边形.
11.A 因为四边形ABCD是正方形,所以AD=AB,∠BAD=∠ABC=∠ADC=90°.如图,延长CB到G,使BG=DF,连接AG,则∠ABG=90°.在△ADF和△ABG中,所以△ADF≌△ABG(SAS),所以AF=AG,∠DAF=∠BAG.因为∠EAF=45°,所以∠BAE+∠DAF=45°,所以∠BAE+∠BAG=45°,所以∠GAE=∠FAE=45°.在△AEF和△AEG中,,所以△AEF≌△AEG(SAS),所以∠AEF=∠AEG.因为∠BAE=α,所以∠AEB=90°-α,所以∠AEF=∠AEB=90°-α,
所以∠FEC=180°-∠AEF-∠AEB=180°-2×(90°-α)=2α,故选A.
12.C 因为四边形ABCD是菱形,
所以AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
所以∠BAG=∠EDG,因为CD=DE,所以AB=DE.在△ABG和△DEG中,所以△ABG≌△DEG(AAS),所以AG=DG,所以OG是△ABD的中位线,所以OG=AB,故①正确;
如图,连接AE,因为AB∥CE,AB=DE,所以四边形ABDE是平行四边形,因为∠BAD=60°,AB=AD,所以△ABD是等边三角形,所以AB=BD,所以平行四边形ABDE是菱形,故③正确;
因为OA=OC,AG=DG,所以S△ACD=2S△AOD,S△AOD=2S△AOG,所以S△ACD=4S△AOG,易知S△AOG=S△BOG,所以S△ACD=4S△BOG,故④正确;
易知S△ABG=S△DBG,OB=AG,∠AOB=∠BGA=90°,
又因为∠BFO=∠AFG,所以△BOF≌△AGF,所以S△BOF=S△AGF,所以S△DBG-S△BOF=S△ABG-S△AGF,即S四边形ODGF=S△ABF,故②错误.
综上,正确的结论是①③④.
二、填空题
13.答案 BE=DF(答案不唯一)
解析 本题通过三角形全等的判定考查平行四边形的性质.添加的条件可以是BE=DF.因为四边形ABCD是平行四边形,所以AB∥CD,∠A=∠C,AB=CD,所以∠E=∠F.因为BE=DF,所以BE+AB=DF+CD,即AE=CF.在△AEG和△CFH中,所以△AEG≌△CFH(ASA).(答案不唯一)
14.答案 (4,2)
解析 如图,延长BC交y轴于点D,因为四边形ABCO是平行四边形,所以BC=OA,BC∥OA.因为OA⊥y轴,所以BC⊥y轴.因为A(3,0),C(1,2),所以BC=OA=3,CD=1,OD=2,所以BD=CD+BC=1+3=4,所以B(4,2).
15.答案 6
解析 因为四边形ABCD是矩形,所以∠BAD=90°,因为F为BE的中点,AF=6,所以BE=2AF=12.因为G,H分别为BC,EC的中点,所以GH是△CBE的中位线,所以GH=BE=6.
16.答案 2或10
解析 设运动的时间为t秒.因为四边形ABCD是平行四边形,AC=12,BD=8,所以OA=OC=AC=6,OB=OD=BD=4.因为AE=CF=t,所以OE=OF=6-t或OE=OF=t-6,所以四边形BEDF是平行四边形,当EF=BD时, BEDF是矩形,此时OE=OD,所以6-t=4或t-6=4,解得t=2或t=10,所以经过2秒或10秒,四边形BEDF是矩形.
17.答案 ①②④
解析 因为四边形ABCD是平行四边形,所以∠ABC=∠ADC=60°,AB∥CD,AD∥BC,所以∠BAD=120°.因为AE平分∠BAD,所以∠BAE=∠EAD=60°,所以△ABE是等边三角形,所以AE=AB=BE,∠AEB=60°.因为AB=BC,所以BE=BC,所以AE=AB=BE=EC,所以∠ACB=∠CAE=∠AEB=30°,因为AD∥BC,所以∠CAD=∠ACB,所以∠CAD=30°,①正确;因为∠BAC=∠BAE+∠CAE=90°,所以AC⊥AB,所以S ABCD=AB·AC,易知S△AOB=S△COB=S△COD=S△AOD,所以S△COD+S△AOB=AB·AC,②正确;因为∠BCD=∠BAD=120°,∠BDC<60°,所以∠BCD与∠BDC不相等,所以BD与BC不相等.因为AB=BC,OB=BD,所以AB与OB不相等,③错误;因为OA=OC,BE=EC,所以OE是△ABC的中位线,所以OE=AB,因为AB=BC,所以OE=BC,④正确.
三、解答题
18.解析 (1)因为CF平分∠BCD,所以∠BCD=2∠BCF=2×65°=130°.因为四边形ABCD是平行四边形,所以AB∥CD,所以∠ABC+∠BCD=180°,所以∠ABC=180°-∠BCD=180°-130°=50°.
(2)证明:因为四边形ABCD是平行四边形,所以AB=CD,AB∥CD,∠BAD=∠DCB,所以∠ABE=∠CDF.由题意知∠BAE=∠BAD,∠DCF=∠DCB,所以∠BAE=∠DCF,所以△ABE≌△CDF(ASA),所以∠AEB=∠CFD,AE=CF,所以∠AEF=∠CFE,所以AE∥CF,所以四边形AECF是平行四边形.
19.解析 (1)证明:因为DE∥AC,CE∥BD,所以四边形OCED是平行四边形.因为四边形ABCD是矩形,所以AC=BD,OC=AC,OD=BD,所以OC=OD,所以四边形OCED是菱形,所以CE=DE.
(2)因为四边形ABCD是矩形,BC=3,DC=2,
所以OA=OB=OC=OD,S矩形ABCD=3×2=6,
所以S△OCD=S矩形ABCD=×6=1.5.
因为四边形OCED是菱形,所以菱形OCED的面积=2S△OCD=2×1.5=3.
20.解析 (1)证明:因为四边形ABCD是正方形,GE⊥CD,
所以∠ADE=∠GEC=90°,所以AD∥GE,所以∠DAG=∠EGH.
(2)AH⊥EF,理由如下:
连接GC交EF于点O,如图,因为四边形ABCD为正方形,所以∠ADG=∠CDG=45°,AD=CD,
又因为DG=DG,所以△ADG≌△CDG(SAS),所以∠DAG=∠DCG.
在正方形ABCD中,∠ECF=90°,因为GE⊥CD,GF⊥BC,所以∠GEC=∠GFC=90°,所以四边形FCEG为矩形,所以OE=OC,所以∠OEC=∠OCE,所以∠DAG=∠OEC.由(1)得∠DAG=∠EGH,所以∠EGH=∠OEC,所以∠EGH+∠GEH=∠OEC+∠GEH=∠GEC=90°,所以∠GHE=90°,所以AH⊥EF.
21.解析 (1)证明:因为四边形ABCD是平行四边形,所以AB∥CD,AB=CD,OB=OD,OA=OC,所以∠ABM=∠CDN,因为点M,N分别是OB,OD的中点,所以BM=DN,所以△ABM≌△CDN(SAS).
(2)当AC=2AB时,四边形MECN是矩形.理由如下:
因为MA=ME,OA=OC,所以OM是△AEC的中位线,所以OM∥EC,OM=EC,易知OM=ON=MN,所以MN=EC,又因为MN∥EC,所以四边形MECN是平行四边形.因为AC=2AB,AC=2OA,所以AB=OA,又点M是OB的中点,所以AM⊥BO,所以∠EMN=90°,所以 MECN是矩形.
(3)当△ANE是等腰直角三角形,且∠ANE=90°时,四边形MECN是正方形.理由:易得四边形MECN是平行四边形.因为∠ANE=90°,EM=AM,所以MN=AE=ME,所以 MECN是菱形,因为AN=EN,EM=AM,所以NM⊥AE,所以∠EMN=90°,所以菱形MECN是正方形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学八年级下学期
第6章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共36分)
1.(2023四川成都中考)如图,在 ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是 ( )
A.AC=BD B.OA=OC
C.AC⊥BD D.∠ADC=∠BCD
2.(2022山东滨州中考)下列命题,其中是真命题的是 ( )
A.对角线互相垂直的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.对角线互相平分的四边形是菱形
D.对角线互相垂直的矩形是正方形
3.如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,连接DE,EF,DF,则图中平行四边形的个数是 ( )
A.2 B.3
C.4 D.5
4.(2023北京清华附中期中)如图,在 ABCD中,AE⊥CD于点E,∠B=60°,则∠DAE等于( )
A.15° B.30° C.45° D.60°
5.【平行线+角平分线】(2023山东聊城东阿、临清期中)如图,在 ABCD中,AD=2AB,CE平分∠BCD,交AD边于点E,且AE=5,则AB的长为( )
A. B.3 C.4 D.5
6.【新考向·尺规作图】(2023湖北随州中考)如图,在 ABCD中,分别以B,D为圆心,大于BD的长为半径画弧,两弧相交于点M,N,过M,N两点作直线交BD于点O,交AD,BC于点E,F,下列结论不正确的是( )
A.AE=CF B.DE=BF C.OE=OF D.DE=DC
7.(2023四川泸州中考)如图, ABCD的对角线AC,BD相交于点O,∠ADC的平分线与边AB相交于点P,E是PD的中点,若AD=4,CD=6,则EO的长为( )
A.1 B.2 C.3 D.4
8.(2023山东菏泽曹县期中)如图,在菱形ABCD中,对角线AC,BD交于点O,DE⊥AB于点E,连接OE,若∠DAB=70°,则∠EOB的度数是( )
A.50° B.60° C.70° D.80°
9.(2022山东聊城东阿期中)若顺次连接四边形ABCD各边中点所得到的四边形是矩形,则四边形ABCD必然是( )
A.菱形
B.对角线互相垂直的四边形
C.正方形
D.对角线相等的四边形
10.【分类讨论思想】(2022山东聊城临清期中)如图,在四边形ABCD中,AD∥BC,AD=8 cm,BC=12 cm,M是BC上一点,且BM=9 cm,点E从点A出发,以1 cm/s的速度向点D运动,点F从点C出发,以3 cm/s的速度向点B运动,当其中一点到达终点时,另一点也随之停止,设运动时间为t(s),当以A、M、E、F为顶点的四边形是平行四边形时,t的值是( )
A. B.3 C.3或 D.或
11.【“半角”全等模型】(2023重庆中考A卷)如图,在正方形 ABCD中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于( )
A.2α B.90°-2α
C.45°-α D.90°-α
12.(2022山东东营垦利期末)如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD的延长线上一点,且CD=DE,连接BE,分别交AC、AD于点F、G,连接OG,下列结论:①OG=AB;②S四边形ODGF>S△ABF;③以点A、B、D、E为顶点的四边形是菱形;④S△ACD=4S△BOG.其中正确的是( )
A.①② B.①②③
C.①③④ D.②③④
二、填空题(每小题3分,共15分)
13.【新考法】(2022湖北荆州中考)如图,点E,F分别在 ABCD的边AB,CD的延长线上,连接EF,分别交AD,BC于G,H.添加一个条件使△AEG≌△CFH,这个条件可以是 .(只需写一种情况)
14.【数形结合思想】(2023四川凉山州中考)如图, ABCO的顶点O、A、C的坐标分别是(0,0)、(3,0)、(1,2),则顶点B的坐标是 .
15.(2022山东潍坊安丘期末)如图,点E是矩形ABCD的边AD上一点,点F,G,H分别是BE,BC,CE的中点,若AF=6,则GH的长为 .
16.【易错题】(2023江苏南京外国语学校期中)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,动点E以每秒1个单位长度的速度从点A出发沿AC方向运动,点F同时以每秒1个单位长度的速度从点C出发沿CA方向运动,若AC=12,BD=8,则经过 秒,四边形BEDF是矩形.
17.(2023山东济南槐荫期中改编)如图, ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S△COD+S△AOB=AB·AC;③OB=AB;④OE=
BC.其中正确的有 .(把所有正确结论的序号都填在横线上)
三、解答题(共49分)
18.(2022江苏常州期中)(12分)如图,四边形ABCD是平行四边形,AE,CF分别平分∠BAD和∠BCD,交BD于点E,F.
(1)若∠BCF=65°,求∠ABC的度数.
(2)连接CE,AF,求证:四边形AECF是平行四边形.
19.【教材变式·P28T7】(2023湖北随州中考改编)(12分)如图,矩形ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.
(1)求证:CE=DE.
(2)若BC=3,DC=2,求四边形OCED的面积.
20.【教材变式·P26例2】(2023浙江绍兴中考)(12分)如图,在正方形ABCD中,G是对角线BD上的一点(与点B,D不重合),GE⊥CD,GF⊥
BC,E,F分别为垂足.连接EF,AG,并延长AG交EF于点H.
(1)求证:∠DAG=∠EGH.
(2)判断AH与EF是否垂直,并说明理由.
21.(13分)如图,在 ABCD中,对角线AC与BD相交于点O,点M,N分别为OB,OD的中点,连接AM并延长至点E,使EM=AM,连接CE,CN.
(1)求证:△ABM≌△CDN.
(2)当AB与AC满足什么数量关系时,四边形MECN是矩形 请说明理由.
(3)连接AN,EN,当△ANE满足什么条件时,四边形MECN是正方形 请说明理由.
答案全解全析
一、选择题
1.B 平行四边形的对角线互相平分,但不一定相等,不一定垂直,选项B正确,选项A,C不一定正确.平行四边形的对角相等,但邻角不一定相等,选项D不一定正确.
2.D
3.B ∵D,E,F分别是AB,BC,CA的中点,
∴DE,DF,EF是△ABC的中位线,
∴DE∥AC,DF∥BC,EF∥AB,
∴四边形EDFC、四边形EBDF、四边形ADEF均是平行四边形.
故选B.
4.B 因为四边形ABCD是平行四边形,所以∠D=∠B=60°,
因为AE⊥CD,所以∠AED=90°,所以∠DAE=90°-∠D=30°.故选B.
5.D 因为四边形ABCD为平行四边形,所以AB=CD,AD∥BC,所以∠DEC=∠ECB,因为CE平分∠BCD,所以∠DCE=∠ECB,所以∠DEC=∠DCE,所以CD=DE.因为AD=2AB,所以AD=2CD=2ED,因为AD=AE+ED,所以ED=AE=5,所以AB=5.故选D.
6.D 根据作图可知,EF垂直平分BD,所以BO=DO.因为四边形ABCD是平行四边形,所以AD=BC,AD∥BC,所以∠EDO=∠FBO,因为∠BOF=∠DOE,所以△BOF≌△DOE(ASA),所以BF=DE,OE=OF,选项B,C正确.因为AD-DE=BC-BF,所以AE=CF,选项A正确.无法证明DE=CD,选项D错误.故选D.
7.A 因为四边形ABCD为平行四边形,所以AB∥DC,AB=CD=6,OD=OB,所以∠CDP=∠APD.因为DP平分∠ADC,所以∠CDP=∠ADP,所以∠ADP=∠APD,所以AP=AD=4,所以PB=AB-AP=6-4=2.因为E是PD的中点,O是BD的中点,所以EO是△DPB的中位线,所以EO=PB=1,故选A.
8.C 因为四边形ABCD是菱形,所以AB=AD,DO=BO.因为∠DAB=70°,所以∠ABD=∠ADB==55°.因为DE⊥AB,所以∠DEB=90°.在Rt△DEB中,因为DO=BO,所以OE=BO=DO=DB,所以∠OEB=∠ABD=55°,所以∠EOB=180°-55°-55°=70°.
9.B 如图,四边形ABCD中,E、F、G、H分别是AB、BC、CD、AD的中点,所以EH∥FG∥BD,EF∥AC∥HG,因为四边形EFGH是矩形,所以EF⊥FG,所以AC⊥BD,故选B.
10.D 因为AD∥BC,所以①当F在线段CM上,且AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,则t=12-9-3t,解得t=;②当点F在线段BM上,且AE=FM时,以A、M、E、F为顶点的四边形是平行四边形,则t=3t-(12-9),解得t=.综上所述,当t=或时,以A、M、E、F为顶点的四边形是平行四边形.
11.A 因为四边形ABCD是正方形,所以AD=AB,∠BAD=∠ABC=∠ADC=90°.如图,延长CB到G,使BG=DF,连接AG,则∠ABG=90°.在△ADF和△ABG中,所以△ADF≌△ABG(SAS),所以AF=AG,∠DAF=∠BAG.因为∠EAF=45°,所以∠BAE+∠DAF=45°,所以∠BAE+∠BAG=45°,所以∠GAE=∠FAE=45°.在△AEF和△AEG中,,所以△AEF≌△AEG(SAS),所以∠AEF=∠AEG.因为∠BAE=α,所以∠AEB=90°-α,所以∠AEF=∠AEB=90°-α,
所以∠FEC=180°-∠AEF-∠AEB=180°-2×(90°-α)=2α,故选A.
12.C 因为四边形ABCD是菱形,
所以AB=BC=CD=DA,AB∥CD,OA=OC,OB=OD,AC⊥BD,
所以∠BAG=∠EDG,因为CD=DE,所以AB=DE.在△ABG和△DEG中,所以△ABG≌△DEG(AAS),所以AG=DG,所以OG是△ABD的中位线,所以OG=AB,故①正确;
如图,连接AE,因为AB∥CE,AB=DE,所以四边形ABDE是平行四边形,因为∠BAD=60°,AB=AD,所以△ABD是等边三角形,所以AB=BD,所以平行四边形ABDE是菱形,故③正确;
因为OA=OC,AG=DG,所以S△ACD=2S△AOD,S△AOD=2S△AOG,所以S△ACD=4S△AOG,易知S△AOG=S△BOG,所以S△ACD=4S△BOG,故④正确;
易知S△ABG=S△DBG,OB=AG,∠AOB=∠BGA=90°,
又因为∠BFO=∠AFG,所以△BOF≌△AGF,所以S△BOF=S△AGF,所以S△DBG-S△BOF=S△ABG-S△AGF,即S四边形ODGF=S△ABF,故②错误.
综上,正确的结论是①③④.
二、填空题
13.答案 BE=DF(答案不唯一)
解析 本题通过三角形全等的判定考查平行四边形的性质.添加的条件可以是BE=DF.因为四边形ABCD是平行四边形,所以AB∥CD,∠A=∠C,AB=CD,所以∠E=∠F.因为BE=DF,所以BE+AB=DF+CD,即AE=CF.在△AEG和△CFH中,所以△AEG≌△CFH(ASA).(答案不唯一)
14.答案 (4,2)
解析 如图,延长BC交y轴于点D,因为四边形ABCO是平行四边形,所以BC=OA,BC∥OA.因为OA⊥y轴,所以BC⊥y轴.因为A(3,0),C(1,2),所以BC=OA=3,CD=1,OD=2,所以BD=CD+BC=1+3=4,所以B(4,2).
15.答案 6
解析 因为四边形ABCD是矩形,所以∠BAD=90°,因为F为BE的中点,AF=6,所以BE=2AF=12.因为G,H分别为BC,EC的中点,所以GH是△CBE的中位线,所以GH=BE=6.
16.答案 2或10
解析 设运动的时间为t秒.因为四边形ABCD是平行四边形,AC=12,BD=8,所以OA=OC=AC=6,OB=OD=BD=4.因为AE=CF=t,所以OE=OF=6-t或OE=OF=t-6,所以四边形BEDF是平行四边形,当EF=BD时, BEDF是矩形,此时OE=OD,所以6-t=4或t-6=4,解得t=2或t=10,所以经过2秒或10秒,四边形BEDF是矩形.
17.答案 ①②④
解析 因为四边形ABCD是平行四边形,所以∠ABC=∠ADC=60°,AB∥CD,AD∥BC,所以∠BAD=120°.因为AE平分∠BAD,所以∠BAE=∠EAD=60°,所以△ABE是等边三角形,所以AE=AB=BE,∠AEB=60°.因为AB=BC,所以BE=BC,所以AE=AB=BE=EC,所以∠ACB=∠CAE=∠AEB=30°,因为AD∥BC,所以∠CAD=∠ACB,所以∠CAD=30°,①正确;因为∠BAC=∠BAE+∠CAE=90°,所以AC⊥AB,所以S ABCD=AB·AC,易知S△AOB=S△COB=S△COD=S△AOD,所以S△COD+S△AOB=AB·AC,②正确;因为∠BCD=∠BAD=120°,∠BDC<60°,所以∠BCD与∠BDC不相等,所以BD与BC不相等.因为AB=BC,OB=BD,所以AB与OB不相等,③错误;因为OA=OC,BE=EC,所以OE是△ABC的中位线,所以OE=AB,因为AB=BC,所以OE=BC,④正确.
三、解答题
18.解析 (1)因为CF平分∠BCD,所以∠BCD=2∠BCF=2×65°=130°.因为四边形ABCD是平行四边形,所以AB∥CD,所以∠ABC+∠BCD=180°,所以∠ABC=180°-∠BCD=180°-130°=50°.
(2)证明:因为四边形ABCD是平行四边形,所以AB=CD,AB∥CD,∠BAD=∠DCB,所以∠ABE=∠CDF.由题意知∠BAE=∠BAD,∠DCF=∠DCB,所以∠BAE=∠DCF,所以△ABE≌△CDF(ASA),所以∠AEB=∠CFD,AE=CF,所以∠AEF=∠CFE,所以AE∥CF,所以四边形AECF是平行四边形.
19.解析 (1)证明:因为DE∥AC,CE∥BD,所以四边形OCED是平行四边形.因为四边形ABCD是矩形,所以AC=BD,OC=AC,OD=BD,所以OC=OD,所以四边形OCED是菱形,所以CE=DE.
(2)因为四边形ABCD是矩形,BC=3,DC=2,
所以OA=OB=OC=OD,S矩形ABCD=3×2=6,
所以S△OCD=S矩形ABCD=×6=1.5.
因为四边形OCED是菱形,所以菱形OCED的面积=2S△OCD=2×1.5=3.
20.解析 (1)证明:因为四边形ABCD是正方形,GE⊥CD,
所以∠ADE=∠GEC=90°,所以AD∥GE,所以∠DAG=∠EGH.
(2)AH⊥EF,理由如下:
连接GC交EF于点O,如图,因为四边形ABCD为正方形,所以∠ADG=∠CDG=45°,AD=CD,
又因为DG=DG,所以△ADG≌△CDG(SAS),所以∠DAG=∠DCG.
在正方形ABCD中,∠ECF=90°,因为GE⊥CD,GF⊥BC,所以∠GEC=∠GFC=90°,所以四边形FCEG为矩形,所以OE=OC,所以∠OEC=∠OCE,所以∠DAG=∠OEC.由(1)得∠DAG=∠EGH,所以∠EGH=∠OEC,所以∠EGH+∠GEH=∠OEC+∠GEH=∠GEC=90°,所以∠GHE=90°,所以AH⊥EF.
21.解析 (1)证明:因为四边形ABCD是平行四边形,所以AB∥CD,AB=CD,OB=OD,OA=OC,所以∠ABM=∠CDN,因为点M,N分别是OB,OD的中点,所以BM=DN,所以△ABM≌△CDN(SAS).
(2)当AC=2AB时,四边形MECN是矩形.理由如下:
因为MA=ME,OA=OC,所以OM是△AEC的中位线,所以OM∥EC,OM=EC,易知OM=ON=MN,所以MN=EC,又因为MN∥EC,所以四边形MECN是平行四边形.因为AC=2AB,AC=2OA,所以AB=OA,又点M是OB的中点,所以AM⊥BO,所以∠EMN=90°,所以 MECN是矩形.
(3)当△ANE是等腰直角三角形,且∠ANE=90°时,四边形MECN是正方形.理由:易得四边形MECN是平行四边形.因为∠ANE=90°,EM=AM,所以MN=AE=ME,所以 MECN是菱形,因为AN=EN,EM=AM,所以NM⊥AE,所以∠EMN=90°,所以菱形MECN是正方形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
