2024青岛版数学八年级下学期--第7章《实数》素养综合检测(含解析)
文档属性
| 名称 | 2024青岛版数学八年级下学期--第7章《实数》素养综合检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 406.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024青岛版数学八年级下学期
第7章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共36分)
1.(2023四川凉山州中考改编)下列各数中,不是无理数的是( )
A. B.3.232 232 223…(每相邻两个3之间2的个数依次多1)
C. D.
2.(2022山东聊城莘县期中)下列各式一定有意义的是( )
A. B. C. D.
3.(2023山东威海中考)面积为9的正方形,其边长等于( )
A.9的平方根 B.9的算术平方根
C.9的立方根 D.的算术平方根
4.(2023山东菏泽定陶期中)下列计算正确的是( )
A.=±5 B.=4
C.=4 D.±=2
5.【数形结合思想】(2023内蒙古赤峰中考)如图,数轴上表示实数的点可能是( )
A.点P B.点Q C.点R D.点S
6.【真实情境】(2022山东潍坊潍城期中)如图,某超市为了吸引顾客,在超市门口离地高4.5 m的墙上安装了一个由传感器控制的门铃A,如图①所示,人只要移动到距该门铃5 m及5 m以内时,门铃就会自动发出语音“欢迎光临”.如图②所示,一位学生走到D处,门铃恰好自动响起,已知该学生的身高CD=1.5 m,则BD的长为( )
图① 图②
A.3 m B.4 m C.5 m D.7 m
7.(2022山东聊城茌平期末)满足下列条件时,△ABC不是直角三角形的是( )
A.AB=1,BC=2,AC=
B.AB2-BC2=AC2
C.∠A-∠B=∠C
D.∠A∶∠B∶∠C=3∶4∶5
8.【新考向·规律探究题】用计算器计算得≈5.036,≈15.925,则≈( )
A.50.36 B.503.6
C.159.25 D.1.592 5
9.【新考向·规律探究题】在学习“勾股数组”的知识时,爱思考的小琦发现了一组有规律的勾股数组,并将它们记录在如下的表格中:
a 6 8 10 12 14 …
b 8 15 24 35 48 …
c 10 17 26 37 50 …
则当a=18时,b+c的值为( )
A.242 B.200 C.128 D.162
10.(2023山东日照中考)已知直角三角形的三边长a,b,c满足c>a>b,分别以a,b,c为边长作三个正方形,把两个较小的正方形放置在最大正方形内,如图,设三个正方形无重叠部分的面积为S1,均重叠部分的面积为S2,则( )
A.S1>S2 B.S1C.S1=S2 D.S1,S2的大小无法确定
11.【折叠问题】(2023山东聊城莘县期中)如图,矩形纸片ABCD沿过点C的直线MN折叠,使得点B落在边AD的中点E处,且AE=1,则矩形的边AB的长度为( )
A.1 B. C. D.2
12.(2023湖北荆州公安期中)如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠OAB=120°,则点E的坐标为( )
A.(3,) B.(,3) C.(,1) D.(1,)
二、填空题(每小题3分,共15分)
13.(2023山东菏泽成武期末)的相反数是 .
14.计算:(-1)2 021-+|-2|+= .
15.(2022湖北黄冈中考改编)勾股定理最早出现在《周髀算经》:“勾广三,股修四,经隅五.”观察下列勾股数:3,4,5;5,12,13;7,24,25;……,这类勾股数的特点:“勾”为奇数,“弦”与“股”的差为1.若此类勾股数的“勾”为m(m≥3,m为正奇数),则其“弦”是 (结果用含m的式子表示).
16.【分类讨论思想】(2022四川南充中考)若为整数,x为正整数,则x的值是 .
17.如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,点O在原点处,在OB上截取BC=BA,以点O为圆心,OC的长为半径画弧,交数轴于点P,则OP的中点D表示的实数是 .
三、解答题(共49分)
18.【新独家原创】(9分)求下列各式中x的值.
(1)25(x-1)2=121; (2)3(x-2)3-81=0;
(3)|x+3|=π.
19.(2023山东聊城东阿期中)(8分)已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是的整数部分.
(1)求a,b,c的值.
(2)求2a+b-c的平方根.
20.(2022山东潍坊寿光期中)(9分)如图,在△ABC中,BC=15,D是线段AB上一点,BD=9,连接CD,CD=12.
(1)求证:CD⊥AB.
(2)若S△ABC=84,求△ABC的周长.
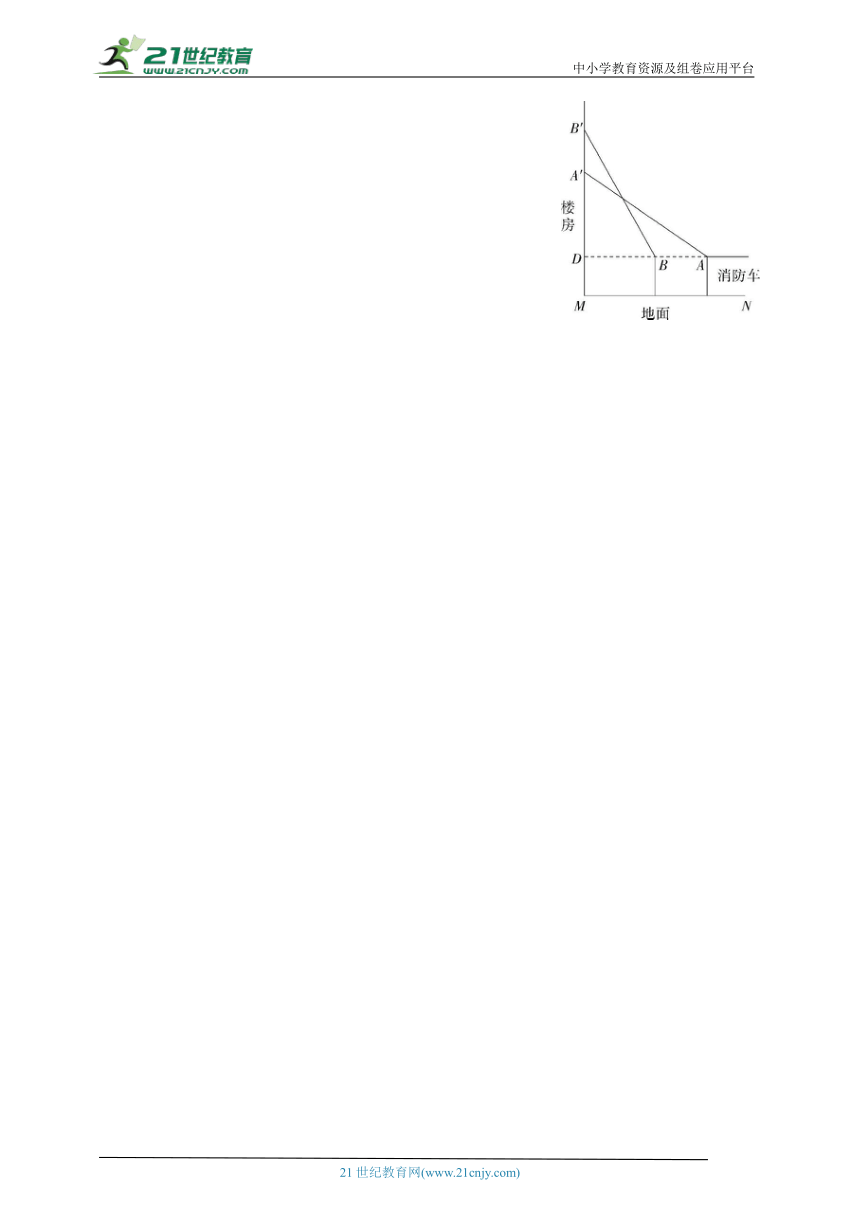
21.(2022山东潍坊昌乐期末)(11分)现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,已知消防车高3 m,云梯最多能伸长到10 m,救人时云梯伸至最长.如图,消防车先在A处完成从9 m高处救人的任务后,前进到B处从12 m高处救人.
(1)求消防车在A处离楼房的距离(AD的长度).
(2)求消防车两次救援移动的距离(AB的长度).(结果精确到0.1 m,参考数据:≈1.73,≈3.16,≈4.36)
22.【分类讨论思想】(2023云南昆明期中)(12分)如图,矩形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
(1)求△ADE的周长.
(2)当t为何值时,△PAE为直角三角形
(3)是否存在这样的t的值,使EA恰好平分∠PED 若存在,求出t的值;若不存在,请说明理由.
答案全解全析
一、选择题
1.A ∵=2,2是有理数,∴选项A符合题意;∵3.232 232 223…(每相邻两个3之间2的个数依次多1),,是无理数,∴选项B,C,D不符合题意.
2.C 选项A,无意义;选项B,当x<0时,无意义;选项C,因为a2+1>0,所以有意义;选项D,当b=0或<0时,无意义.
3.B ∵正方形的面积为9,∴其边长=,故选B.
4.C =5,=-4,=(-2)2=4,±=±2,选项A,B,D错误,选项C正确.
5.B ∵4<7<9,∴<<,∴2<<3.故选B.
6.B 过点C作CE⊥AB于点E(图略).
由题意可知,BE=CD=1.5 m,AC=5 m,BD=CE,
∴AE=AB-BE=4.5-1.5=3(m),
由勾股定理,得BD=CE==4(m),
故BD的长为4 m.
7.D 选项A,∵12+()2=22,∴AB2+AC2=BC2,∴△ABC是直角三角形;选项B,∵AB2-BC2=AC2,∴AB2=BC2+AC2,∴△ABC是直角三角形;选项C,∵∠A-∠B=∠C,∠A+∠B+∠C=180°,∴∠A=90°,∴△ABC是直角三角形;选项D,∵∠A∶∠B∶∠C=3∶4∶5,∠A+∠B+∠C=180°,
∴∠A=45°,∠B=60°,∠C=75°,∴△ABC不是直角三角形.故选D.
8.B 一个正数的小数点向左(或向右)移动2n位(n为正整数),它的算术平方根的小数点就向左(或向右)移动n位.≈503.6,故选B.
9.D 根据题中表格的数据可得a2+b2=c2,且c=b+2,则a2+b2=(b+2)2,当a=18时,182+b2=(b+2)2,解得b=80,∴c=80+2=82,∴b+c=162.
10.C ∵直角三角形的三边长a,b,c满足c>a>b,
∴直角三角形的斜边长为c,∴c2=a2+b2,
∵S2=b(a+b-c)=ab+b2-bc,S1=c2-a2-[b2-b(a+b-c)]=ab+b2-bc,
∴S1=S2,故选C.
11.C 如图,连接BE,∵点E为AD的中点,AE=1,
∴DE=AE=1,AD=2AE=2.
∵四边形ABCD是矩形,∴BC=AD=2,AB=CD,∠D=90°.
由折叠的性质,得直线MN是线段BE的垂直平分线,∴EC=BC=2.
在Rt△CDE中,由勾股定理,得DC===,
∴AB=CD=,故选C.
12.A 过点E作EF⊥x轴于点F(图略),∴∠AFE=90°.
∵四边形OABC为菱形,∠OAB=120°,
∴∠FAE=60°,AC⊥OB,∴∠AEO=90°,
∴∠AOE=90°-∠OAE=30°.
∵A(4,0),∴OA=4,∴AE=OA=×4=2.
在Rt△AFE中,∵∠AFE=90°,∴∠AEF=90°-60°=30°,∴AF=AE=1,
∴EF===,OF=AO-AF=4-1=3,∴E(3,).
二、填空题
13.答案
解析 根据立方根的性质可知,=-,
因为-的相反数是,
所以的相反数是.
14.答案 3-
解析 原式=-1-2+2-+4=3-.
15.答案
解析 设其“股”是a,则其“弦”为a+1,根据勾股定理得,m2+a2=(a+1)2,解得a=,所以其“弦”是+1=.
16.答案 4或7或8
解析 ∵为整数,x为正整数,∴=0或1或2.当=0时,8-x=0,解得x=8;当=1时,8-x=1,解得x=7;当=2时,8-x=4,解得x=4.综上,x的值是4或7或8.
17.答案
解析 在Rt△OAB中,由勾股定理,得OB===,又∵BC=BA=1,∴OP=OC=OB-BC=-1,
∵点D是OP的中点,
∴OD=OP=,
故点D表示的实数为.
三、解答题
18.解析 (1)25(x-1)2=121,等式两边都除以25,得(x-1)2=,开平方,得x-1=±,所以x=1±,即x=或x=-.
(2)3(x-2)3-81=0,移项,得3(x-2)3=81,等式两边都除以3,得(x-2)3=27,开立方,得x-2=3,所以x=5.
(3)由题意,得x+3=±π,解得x=-3+π或x=-3-π.
19.解析 (1)∵5a+2的立方根是3,3a+b-1的算术平方根是4,
∴5a+2=33=27,3a+b-1=42=16,解关于a,b的方程组,得a=5,b=2.
∵9<13<16,∴<<,∴3<<4,
所以的整数部分为3,∴c=3.
(2)∵a=5,b=2,c=3,
∴2a+b-c=2×5+2-3=9,9的平方根是±=±3,
∴2a+b-c的平方根是±3.
20.解析 (1)证明:在△BDC中,BC=15,BD=9,CD=12,
∴BD2+CD2=92+122=225,BC2=152=225,
∴BD2+CD2=BC2,∴△BDC是直角三角形,且∠BDC=90°,∴CD⊥AB.
(2)∵S△ABC=AB·CD=84,CD=12,∴AB=14,∴AD=AB-BD=14-9=5.
∵CD⊥AB,∴∠ADC=90°,在Rt△ADC中,由勾股定理,得AC===13,∴△ABC的周长=13+14+15=42.
21.解析 (1)由题意得DM=3 m,AA'=10 m,A'M=9 m,
∴A'D=A'M-DM=9-3=6(m).在Rt△AA'D中,AD==8(m).
答:消防车在A处离楼房的距离为8 m.
(2)由题意得DM=3 m,BB'=10 m,B'M=12 m,
∴B'D=B'M-DM=12-3=9(m).
在Rt△BB'D中,BD===≈4.36(m),
∴AB=AD-BD=8-4.36≈3.6(m).
答:消防车两次救援移动的距离约为3.6 m.
22.解析 (1)∵四边形ABCD是矩形,
∴CD=AB=9,∠D=90°,∴DE=CD-CE=9-6=3.
在Rt△ADE中,∵AD=4,∴AE===5,
∴△ADE的周长为4+3+5=12.
(2)根据题意,得BP=t,则AP=9-t,当△PAE是直角三角形时,分两种情况考虑:①若∠PEA=90°,如图1,过点P作PH⊥CD于H,∴∠PHC=∠PHE=90°.
∵四边形ABCD是矩形,∴∠B=∠C=90°,
∴四边形BCHP是矩形,∴CH=BP=t,PH=BC=4,
∴HE=CE-CH=6-t.
在Rt△PHE中,PE2=HE2+PH2=(6-t)2+42.
在Rt△PEA中,根据勾股定理,得PE2+AE2=AP2,
∴(6-t)2+42+52=(9-t)2,解得t=;
②若∠EPA=90°,如图2,
∵四边形ABCD是矩形,∴∠D=∠DAB=90°,
∴四边形ADEP是矩形,∴AP=DE=3,
∴BP=AB-AP=6,∴t=6.
综上所述,当t=6或时,△PAE为直角三角形.
(3)存在t=,使EA恰好平分∠PED.理由:
如图3,过点E作EM⊥AB于点M.
假设EA平分∠PED,∴∠PEA=∠DEA.
易知CD∥AB,∴∠DEA=∠EAP,∴∠PEA=∠EAP,
∴PE=PA,∴PE2=PA2,
易知EM=AD=4,PM=PA-AM=PA-ED=9-t-3=6-t,
∴PE2=EM2+PM2=42+(6-t)2,∴(6-t)2+42=(9-t)2,解得t=,
∴存在t=,使EA恰好平分∠PED.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学八年级下学期
第7章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共36分)
1.(2023四川凉山州中考改编)下列各数中,不是无理数的是( )
A. B.3.232 232 223…(每相邻两个3之间2的个数依次多1)
C. D.
2.(2022山东聊城莘县期中)下列各式一定有意义的是( )
A. B. C. D.
3.(2023山东威海中考)面积为9的正方形,其边长等于( )
A.9的平方根 B.9的算术平方根
C.9的立方根 D.的算术平方根
4.(2023山东菏泽定陶期中)下列计算正确的是( )
A.=±5 B.=4
C.=4 D.±=2
5.【数形结合思想】(2023内蒙古赤峰中考)如图,数轴上表示实数的点可能是( )
A.点P B.点Q C.点R D.点S
6.【真实情境】(2022山东潍坊潍城期中)如图,某超市为了吸引顾客,在超市门口离地高4.5 m的墙上安装了一个由传感器控制的门铃A,如图①所示,人只要移动到距该门铃5 m及5 m以内时,门铃就会自动发出语音“欢迎光临”.如图②所示,一位学生走到D处,门铃恰好自动响起,已知该学生的身高CD=1.5 m,则BD的长为( )
图① 图②
A.3 m B.4 m C.5 m D.7 m
7.(2022山东聊城茌平期末)满足下列条件时,△ABC不是直角三角形的是( )
A.AB=1,BC=2,AC=
B.AB2-BC2=AC2
C.∠A-∠B=∠C
D.∠A∶∠B∶∠C=3∶4∶5
8.【新考向·规律探究题】用计算器计算得≈5.036,≈15.925,则≈( )
A.50.36 B.503.6
C.159.25 D.1.592 5
9.【新考向·规律探究题】在学习“勾股数组”的知识时,爱思考的小琦发现了一组有规律的勾股数组,并将它们记录在如下的表格中:
a 6 8 10 12 14 …
b 8 15 24 35 48 …
c 10 17 26 37 50 …
则当a=18时,b+c的值为( )
A.242 B.200 C.128 D.162
10.(2023山东日照中考)已知直角三角形的三边长a,b,c满足c>a>b,分别以a,b,c为边长作三个正方形,把两个较小的正方形放置在最大正方形内,如图,设三个正方形无重叠部分的面积为S1,均重叠部分的面积为S2,则( )
A.S1>S2 B.S1
11.【折叠问题】(2023山东聊城莘县期中)如图,矩形纸片ABCD沿过点C的直线MN折叠,使得点B落在边AD的中点E处,且AE=1,则矩形的边AB的长度为( )
A.1 B. C. D.2
12.(2023湖北荆州公安期中)如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠OAB=120°,则点E的坐标为( )
A.(3,) B.(,3) C.(,1) D.(1,)
二、填空题(每小题3分,共15分)
13.(2023山东菏泽成武期末)的相反数是 .
14.计算:(-1)2 021-+|-2|+= .
15.(2022湖北黄冈中考改编)勾股定理最早出现在《周髀算经》:“勾广三,股修四,经隅五.”观察下列勾股数:3,4,5;5,12,13;7,24,25;……,这类勾股数的特点:“勾”为奇数,“弦”与“股”的差为1.若此类勾股数的“勾”为m(m≥3,m为正奇数),则其“弦”是 (结果用含m的式子表示).
16.【分类讨论思想】(2022四川南充中考)若为整数,x为正整数,则x的值是 .
17.如图,Rt△OAB的直角边OA=2,AB=1,OA在数轴上,点O在原点处,在OB上截取BC=BA,以点O为圆心,OC的长为半径画弧,交数轴于点P,则OP的中点D表示的实数是 .
三、解答题(共49分)
18.【新独家原创】(9分)求下列各式中x的值.
(1)25(x-1)2=121; (2)3(x-2)3-81=0;
(3)|x+3|=π.
19.(2023山东聊城东阿期中)(8分)已知5a+2的立方根是3,3a+b-1的算术平方根是4,c是的整数部分.
(1)求a,b,c的值.
(2)求2a+b-c的平方根.
20.(2022山东潍坊寿光期中)(9分)如图,在△ABC中,BC=15,D是线段AB上一点,BD=9,连接CD,CD=12.
(1)求证:CD⊥AB.
(2)若S△ABC=84,求△ABC的周长.
21.(2022山东潍坊昌乐期末)(11分)现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,已知消防车高3 m,云梯最多能伸长到10 m,救人时云梯伸至最长.如图,消防车先在A处完成从9 m高处救人的任务后,前进到B处从12 m高处救人.
(1)求消防车在A处离楼房的距离(AD的长度).
(2)求消防车两次救援移动的距离(AB的长度).(结果精确到0.1 m,参考数据:≈1.73,≈3.16,≈4.36)
22.【分类讨论思想】(2023云南昆明期中)(12分)如图,矩形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.点P从点B出发,以每秒1个单位的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t秒.
(1)求△ADE的周长.
(2)当t为何值时,△PAE为直角三角形
(3)是否存在这样的t的值,使EA恰好平分∠PED 若存在,求出t的值;若不存在,请说明理由.
答案全解全析
一、选择题
1.A ∵=2,2是有理数,∴选项A符合题意;∵3.232 232 223…(每相邻两个3之间2的个数依次多1),,是无理数,∴选项B,C,D不符合题意.
2.C 选项A,无意义;选项B,当x<0时,无意义;选项C,因为a2+1>0,所以有意义;选项D,当b=0或<0时,无意义.
3.B ∵正方形的面积为9,∴其边长=,故选B.
4.C =5,=-4,=(-2)2=4,±=±2,选项A,B,D错误,选项C正确.
5.B ∵4<7<9,∴<<,∴2<<3.故选B.
6.B 过点C作CE⊥AB于点E(图略).
由题意可知,BE=CD=1.5 m,AC=5 m,BD=CE,
∴AE=AB-BE=4.5-1.5=3(m),
由勾股定理,得BD=CE==4(m),
故BD的长为4 m.
7.D 选项A,∵12+()2=22,∴AB2+AC2=BC2,∴△ABC是直角三角形;选项B,∵AB2-BC2=AC2,∴AB2=BC2+AC2,∴△ABC是直角三角形;选项C,∵∠A-∠B=∠C,∠A+∠B+∠C=180°,∴∠A=90°,∴△ABC是直角三角形;选项D,∵∠A∶∠B∶∠C=3∶4∶5,∠A+∠B+∠C=180°,
∴∠A=45°,∠B=60°,∠C=75°,∴△ABC不是直角三角形.故选D.
8.B 一个正数的小数点向左(或向右)移动2n位(n为正整数),它的算术平方根的小数点就向左(或向右)移动n位.≈503.6,故选B.
9.D 根据题中表格的数据可得a2+b2=c2,且c=b+2,则a2+b2=(b+2)2,当a=18时,182+b2=(b+2)2,解得b=80,∴c=80+2=82,∴b+c=162.
10.C ∵直角三角形的三边长a,b,c满足c>a>b,
∴直角三角形的斜边长为c,∴c2=a2+b2,
∵S2=b(a+b-c)=ab+b2-bc,S1=c2-a2-[b2-b(a+b-c)]=ab+b2-bc,
∴S1=S2,故选C.
11.C 如图,连接BE,∵点E为AD的中点,AE=1,
∴DE=AE=1,AD=2AE=2.
∵四边形ABCD是矩形,∴BC=AD=2,AB=CD,∠D=90°.
由折叠的性质,得直线MN是线段BE的垂直平分线,∴EC=BC=2.
在Rt△CDE中,由勾股定理,得DC===,
∴AB=CD=,故选C.
12.A 过点E作EF⊥x轴于点F(图略),∴∠AFE=90°.
∵四边形OABC为菱形,∠OAB=120°,
∴∠FAE=60°,AC⊥OB,∴∠AEO=90°,
∴∠AOE=90°-∠OAE=30°.
∵A(4,0),∴OA=4,∴AE=OA=×4=2.
在Rt△AFE中,∵∠AFE=90°,∴∠AEF=90°-60°=30°,∴AF=AE=1,
∴EF===,OF=AO-AF=4-1=3,∴E(3,).
二、填空题
13.答案
解析 根据立方根的性质可知,=-,
因为-的相反数是,
所以的相反数是.
14.答案 3-
解析 原式=-1-2+2-+4=3-.
15.答案
解析 设其“股”是a,则其“弦”为a+1,根据勾股定理得,m2+a2=(a+1)2,解得a=,所以其“弦”是+1=.
16.答案 4或7或8
解析 ∵为整数,x为正整数,∴=0或1或2.当=0时,8-x=0,解得x=8;当=1时,8-x=1,解得x=7;当=2时,8-x=4,解得x=4.综上,x的值是4或7或8.
17.答案
解析 在Rt△OAB中,由勾股定理,得OB===,又∵BC=BA=1,∴OP=OC=OB-BC=-1,
∵点D是OP的中点,
∴OD=OP=,
故点D表示的实数为.
三、解答题
18.解析 (1)25(x-1)2=121,等式两边都除以25,得(x-1)2=,开平方,得x-1=±,所以x=1±,即x=或x=-.
(2)3(x-2)3-81=0,移项,得3(x-2)3=81,等式两边都除以3,得(x-2)3=27,开立方,得x-2=3,所以x=5.
(3)由题意,得x+3=±π,解得x=-3+π或x=-3-π.
19.解析 (1)∵5a+2的立方根是3,3a+b-1的算术平方根是4,
∴5a+2=33=27,3a+b-1=42=16,解关于a,b的方程组,得a=5,b=2.
∵9<13<16,∴<<,∴3<<4,
所以的整数部分为3,∴c=3.
(2)∵a=5,b=2,c=3,
∴2a+b-c=2×5+2-3=9,9的平方根是±=±3,
∴2a+b-c的平方根是±3.
20.解析 (1)证明:在△BDC中,BC=15,BD=9,CD=12,
∴BD2+CD2=92+122=225,BC2=152=225,
∴BD2+CD2=BC2,∴△BDC是直角三角形,且∠BDC=90°,∴CD⊥AB.
(2)∵S△ABC=AB·CD=84,CD=12,∴AB=14,∴AD=AB-BD=14-9=5.
∵CD⊥AB,∴∠ADC=90°,在Rt△ADC中,由勾股定理,得AC===13,∴△ABC的周长=13+14+15=42.
21.解析 (1)由题意得DM=3 m,AA'=10 m,A'M=9 m,
∴A'D=A'M-DM=9-3=6(m).在Rt△AA'D中,AD==8(m).
答:消防车在A处离楼房的距离为8 m.
(2)由题意得DM=3 m,BB'=10 m,B'M=12 m,
∴B'D=B'M-DM=12-3=9(m).
在Rt△BB'D中,BD===≈4.36(m),
∴AB=AD-BD=8-4.36≈3.6(m).
答:消防车两次救援移动的距离约为3.6 m.
22.解析 (1)∵四边形ABCD是矩形,
∴CD=AB=9,∠D=90°,∴DE=CD-CE=9-6=3.
在Rt△ADE中,∵AD=4,∴AE===5,
∴△ADE的周长为4+3+5=12.
(2)根据题意,得BP=t,则AP=9-t,当△PAE是直角三角形时,分两种情况考虑:①若∠PEA=90°,如图1,过点P作PH⊥CD于H,∴∠PHC=∠PHE=90°.
∵四边形ABCD是矩形,∴∠B=∠C=90°,
∴四边形BCHP是矩形,∴CH=BP=t,PH=BC=4,
∴HE=CE-CH=6-t.
在Rt△PHE中,PE2=HE2+PH2=(6-t)2+42.
在Rt△PEA中,根据勾股定理,得PE2+AE2=AP2,
∴(6-t)2+42+52=(9-t)2,解得t=;
②若∠EPA=90°,如图2,
∵四边形ABCD是矩形,∴∠D=∠DAB=90°,
∴四边形ADEP是矩形,∴AP=DE=3,
∴BP=AB-AP=6,∴t=6.
综上所述,当t=6或时,△PAE为直角三角形.
(3)存在t=,使EA恰好平分∠PED.理由:
如图3,过点E作EM⊥AB于点M.
假设EA平分∠PED,∴∠PEA=∠DEA.
易知CD∥AB,∴∠DEA=∠EAP,∴∠PEA=∠EAP,
∴PE=PA,∴PE2=PA2,
易知EM=AD=4,PM=PA-AM=PA-ED=9-t-3=6-t,
∴PE2=EM2+PM2=42+(6-t)2,∴(6-t)2+42=(9-t)2,解得t=,
∴存在t=,使EA恰好平分∠PED.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
