2024青岛版数学八年级下学期--第10章《一次函数》素养综合检测(含解析)
文档属性
| 名称 | 2024青岛版数学八年级下学期--第10章《一次函数》素养综合检测(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 475.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024青岛版数学八年级下学期
第10章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共36分)
1.(2023湖南长沙实验教育集团期中)下列函数是正比例函数的是( )
A.y= B.y= C.y=x2+1 D.y=3x+1
2.(2022湖南邵阳中考)在直角坐标系中,已知点A,点B是直线y=kx+b上的两点,则m,n的大小关系是( )
A.mn C.m≥n D.m≤n
3.(2022陕西中考)在同一平面直角坐标系中,直线y=-x+4与y=2x+m相交于点P(3,n),则关于x,y的方程组的解为( )
A. B. C. D.
4.(2023四川乐山中考)下列各点在函数y=2x-1图象上的是( )
A.(-1,3) B.(0,1) C.(1,-1) D.(2,3)
5.(2022辽宁抚顺中考)如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图象分别为直线l1和直线l2,下列结论正确的是( )
A.k1·k2<0 B.k1+k2<0
C.b1-b2<0 D.b1·b2<0
6.(2023内蒙古包头中考)在平面直角坐标系中,将正比例函数y=-2x的图象向右平移3个单位长度得到一次函数y=kx+b(k≠0)的图象,则该一次函数的解析式为( )
A.y=-2x+3 B.y=-2x+6
C.y=-2x-3 D.y=-2x-6
7.(2023四川成都七中期中)如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )
A.x>2 B.x<2
C.x>-1 D.x<-1
8.(2023山东聊城高唐期末)如图,点A(-2,6),B(-4,2),当直线y=kx-2(k≠0)与线段AB有交点时,k的取值范围是( )
A.k≤-1 B.k≥-4
C.k≤-4或k≥-1 D.-4≤k≤-1
9.(2021四川资阳中考改编)一对变量满足如图所示的函数关系.设计以下问题情境:①小明从家骑车以600米/分的速度匀速骑了2.5分钟,在原地停留了2分钟,然后以1 000米/分的速度匀速骑回家.设所用时间为x分钟,离家的距离为y千米.②有一个容积为1.5升的开口空瓶子,小张以0.6升/秒的速度匀速向这个瓶子里注水,注满后停止,等2秒后,再以1升/秒的速度匀速倒出瓶子中的水.设所用时间为x秒,瓶子内水的体积为y升.③在矩形ABCD中,AB=1.5,BC=2,点P从点A出发,沿路线AC—CD—DA运动至点A停止.设点P的运动路程为x,△ABP的面积为y.其中,符合图中函数关系的情境个数为( )
A.3 B.2 C.1 D.0
10.在同一平面直角坐标系中,一次函数y=ax+a2与y=a2x+a的图象可能是( )
A B C D
11.(2023河北石家庄外国语教育集团期中)为了节约水资源,自来水公司按分段收费标准收费,下图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.按照分段收费标准,小颖家三、四月份分别交水费29元和19.8元,则四月份比三月份节约用水( )
A.2吨 B.2.5吨
C.3吨 D.3.5吨
12.【山东常考·最值问题】如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
A.(0,0) B. C. D.
二、填空题(每小题3分,共15分)
13.(2023山东滨州阳信期中)已知函数y=(m-2)+6是关于x的一次函数,则m= .
14.(2023山东潍坊临朐期末)某种小汽车加满油箱,且正常行驶时,油箱中的剩余油量Q(升)与行驶里程x(千米)的关系式为Q=45-0.09x.从关系式可知这种小汽车加满油箱最多可以行驶 千米.
15.(2022山东菏泽单县期末)如图,已知直线l1:y=-2x+4与x轴、y轴分别交于A、B两点,那么过原点O且将△AOB的面积平分的直线l2的表达式为 .
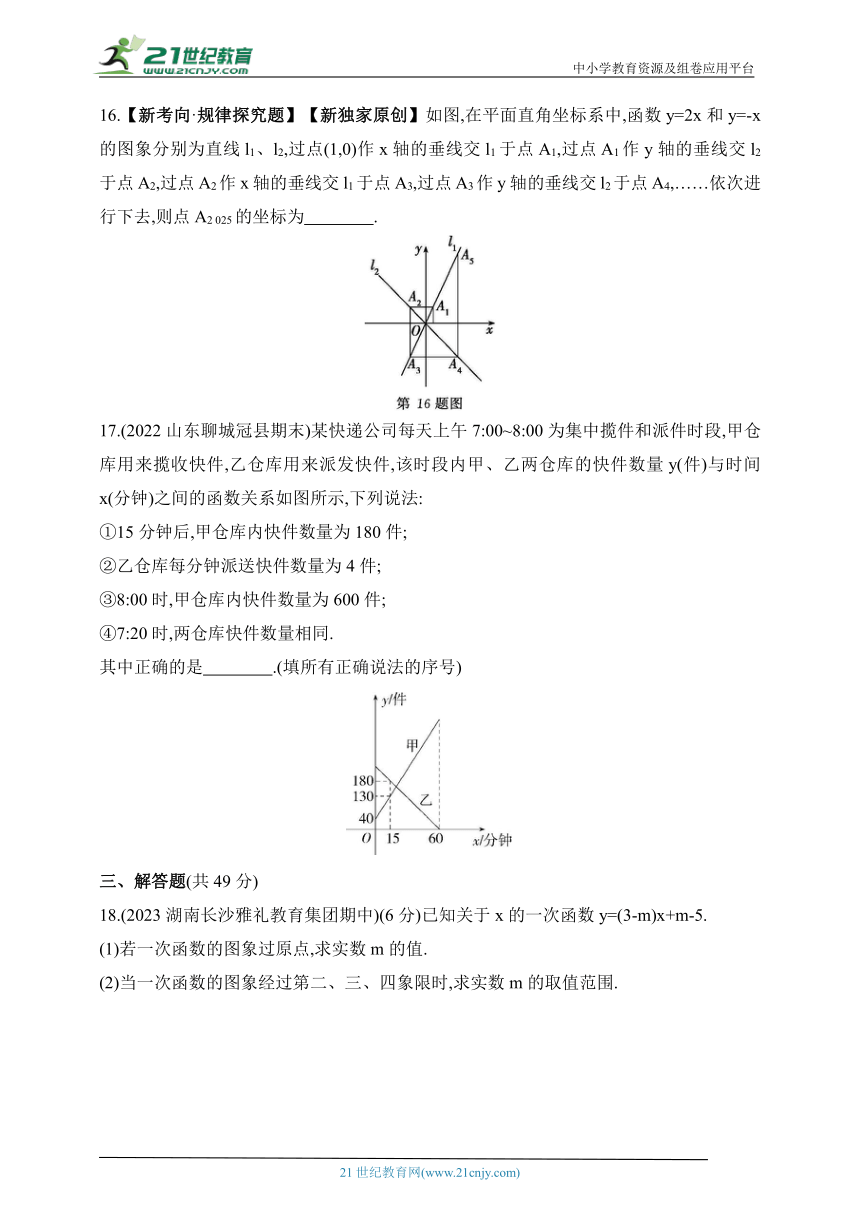
16.【新考向·规律探究题】【新独家原创】如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1、l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,……依次进行下去,则点A2 025的坐标为 .
17.(2022山东聊城冠县期末)某快递公司每天上午7:00~8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分钟)之间的函数关系如图所示,下列说法:
①15分钟后,甲仓库内快件数量为180件;
②乙仓库每分钟派送快件数量为4件;
③8:00时,甲仓库内快件数量为600件;
④7:20时,两仓库快件数量相同.
其中正确的是 .(填所有正确说法的序号)
三、解答题(共49分)
18.(2023湖南长沙雅礼教育集团期中)(6分)已知关于x的一次函数y=(3-m)x+m-5.
(1)若一次函数的图象过原点,求实数m的值.
(2)当一次函数的图象经过第二、三、四象限时,求实数m的取值范围.
19.【跨学科·物理】(2022陕西中考)(7分)在测浮力的实验中,将一长方体石块由玻璃器皿的上方,向下缓慢移动浸入水里的过程中,弹簧测力计的示数F拉力(N)与石块下降的高度x(cm)之间的关系如图所示.
(1)求AB所在直线的函数表达式.
(2)当石块下降的高度为8 cm时,求该石块所受浮力的大小.
(温馨提示:当石块位于水面上方时,F拉力=G重力;当石块入水后,F拉力=G重力-F浮力)
20.(2023湖南永州中考)(8分)小明观察到一个水龙头因损坏而不断地滴水,为探究其漏水造成的浪费情况,小明用一个带有刻度的量筒放在水龙头下面装水,每隔一分钟记录量筒中的总水量,但由于操作延误,开始计时的时候量筒中已经有少量水,因而得到如下表所示的一组数据:
时间t(单位:分钟) 1 2 3 4 5 …
总水量y(单位:毫升) 7 12 17 22 27 …
(1)探究:根据上表中的数据,请判断总水量y与时间t的函数关系,并求出y关于t的表达式.
(2)应用:①请你估算小明在第20分钟测量时量筒中的总水量是多少毫升.
②一个人一天大约饮用1 500毫升水,请你估算这个水龙头一个月(按30天计)的漏水量可供一人饮用多少天.
21.(2023山东聊城莘县期末)(8分)直线y1=-x+3和直线y2=kx-2分别交y轴于点A、B,两直线交于点C(2,m).
(1)求m、k的值.
(2)求△ABC的面积.
(3)在直线y2上存在异于点C的另一点P,使得△ABP与△ABC的面积相等,请求出点P的坐标.
22.(2023山东济南中考)(10分)某校开设智能机器人编程的校本课程,购买了A,B两种型号的机器人模型.A型机器人模型单价比B型机器人模型单价多200元,用2 000元购买A型机器人模型和用1 200元购买B型机器人模型的数量相同.
(1)求A,B两种型号的机器人模型的单价分别是多少元.
(2)学校准备再次购买A,B两种型号的机器人模型共40台,购买B型机器人模型不超过A型机器人模型的3倍,且商家给出了两种型号机器人模型均打八折的优惠.问:购买A,B两种型号的机器人模型各多少台时花费最少 最少花费是多少元
23.(2023山西运城实验中学期中)(10分)如图,在平面直角坐标系中,一次函数y=-x+4的图象分别交x轴、y轴于点A、B,点C在y轴上,AC平分∠OAB.
(1)求点A、B的坐标.
(2)求线段BC的长.
(3)在平面直角坐标系中是否存在点D,使得△ABD是以AB为直角边的等腰直角三角形 若存在,请直接写出点D的坐标;若不存在,请说明理由.
答案全解全析
一、选择题
1.A 形如y=kx(k为常数且k≠0)的函数叫做正比例函数,y=是正比例函数,故选A.
2.A 因为k<0,所以一次函数y=kx+b中,y随x的增大而减小,
因为点A,点B是直线y=kx+b(k<0)上的两点,>,
所以m3.C 将点P(3,n)代入y=-x+4,得n=-3+4=1,所以P(3,1),所以关于x,y的方程组的解为故选C.
4.D A.把x=-1代入y=2x-1,得y=2×(-1)-1=-3,∴点(-1,3)不在函数y=2x-1的图象上;B.把x=0代入y=2x-1,得y=2×0-1=-1,∴点(0,1)不在函数y=2x-1的图象上;C.把x=1代入y=2x-1,得y=2×1-1=1,∴点(1,-1)不在函数y=2x-1的图象上;D.把x=2代入y=2x-1,得y=2×2-1=3,∴点(2,3)在函数y=2x-1的图象上.故选D.
5.D ∵一次函数y=k1x+b1的图象经过第一、二、三象限,∴k1>0,b1>0,∵一次函数y=k2x+b2的图象经过第一、三、四象限,∴k2>0,b2<0,所以k1·k2>0,k1+k2>0,b1-b2>0,b1·b2<0.
6.B 正比例函数y=-2x的图象向右平移3个单位长度,得到的一次函数图象的解析式为y=-2(x-3)=-2x+6.
7.D ∵函数y1=-2x的图象过点A(m,2),∴-2m=2,解得m=-1,∴A(-1,2),由题图可知不等式-2x>ax+3的解集为x<-1.
8.D 当直线过点A时,将A(-2,6)代入y=kx-2中,得6=-2k-2,解得k=-4;当直线过点B时,将B(-4,2)代入y=kx-2中,得2=-4k-2,解得k=-1,易知直线y=kx-2与y轴交于点(0,-2),结合题图可知,当直线y=kx-2与线段AB有交点时,k的取值范围为-4≤k≤-1,故选D.
9.B ①小明从家骑车以600米/分的速度匀速骑了2.5分钟,离家的距离为600×2.5=1 500(米)=1.5(千米),原地停留2分钟,2.5+2=4.5(分钟),返回需要的时间为1 500÷1 000=1.5(分钟),4.5+1.5=6(分钟),符合题意;②将瓶子注满水所用的时间为1.5÷0.6=2.5(秒),2.5+2=4.5(秒),倒出瓶子中的水所用时间为1.5÷1=1.5(秒),4.5+1.5=6(秒),符合题意;③根据勾股定理,得AC===2.5,当点P在AC上运动时,y随x的增大而增大,运动到C点时,x=2.5,y=×2×1.5=1.5,当点P在CD上运动时,y=1.5,运动到点D时,x=2.5+1.5=4,当点P在AD上运动时,y随x的增大而减小,结合题图可知,③不符合题意.故选B.
10.D 对于y=ax+a2与y=a2x+a,当x=1时,两函数的值都是a2+a,所以两直线的交点的横坐标为1.①若a>0,则直线y=ax+a2与y=a2x+a都经过第一、二、三象限;②若a<0,则直线y=ax+a2经过第一、二、四象限,直线y=a2x+a经过第一、三、四象限,故选D.
11.C 当0≤x<10时,设y与x的函数关系式为y=mx(m≠0),由题意得22=10m,解得m=2.2,所以y=2.2x.当x≥10时,设y与x的函数关系式为y=kx+b(k≠0),把(10,22)与(20,57)代入y=kx+b,得解得所以y=3.5x-13.综上,y=因为y=29>22,所以x>10,将y=29代入y=3.5x-13,得29=3.5x-13,解得x=12.因为y=19.8<22,所以0≤x<10,将y=19.8代入y=2.2x,得19.8=2.2x,解得x=9,所以四月份比三月份节约用水12-9=3(吨).
12.B 如图,过点A作AB'⊥OB,垂足为点B',由垂线段最短可知,当点B与点B'重合时,AB最短.因为点B'在直线y=x上,所以∠AOB'=45°,因为AB'⊥OB',所以△AOB'是等腰直角三角形.过点B'作B'C⊥x轴,垂足为C,则△B'CO为等腰直角三角形,因为点A的坐标为(-1,0),所以OA=1,所以OC=CB'=OA=×1=,所以点B'的坐标为,故当线段AB最短时,点B的坐标为.
二、填空题
13.答案 -2
解析 ∵函数y=(m-2)+6是关于x的一次函数,
∴m-2≠0且m2-3=1,∴m=-2.
14.答案 500
解析 把Q=0代入Q=45-0.09x,得45-0.09x=0,解得x=500,
即这种小汽车加满油箱最多可以行驶500千米.
15.答案 y=2x
解析 把x=0代入y=-2x+4,得y=4,则B(0,4),把y=0代入y=-2x+4,得-2x+4=0,解得x=2,则A(2,0),所以线段AB的中点的坐标为(1,2).设直线l2的表达式为y=kx(k≠0),把(1,2)代入,得k=2,所以直线l2的表达式为y=2x.
16.答案 (21 012,21 013)
解析 ∵过点(1,0)作x轴的垂线交l1于点A1,∴A1(1,2),把y=2代入y=-x,得x=-2,即A2(-2,2),把x=-2代入y=2x,得y=-4,即A3(-2,-4),同理可得A4(4,-4),A5(4,8),∴点A2n+1(n为自然数)的横坐标为(-2)n,点A2n+1的纵坐标为2×(-2)n.∵2 025=1 012×2+1,∴A2 025的横坐标为(-2)1 012=21 012,纵坐标为2×(-2)1 012=21 013,∴A2 025的坐标为(21 012,21 013).
17.答案 ②④
解析 由图象可知,对于甲仓库,当x=15时,y=130,即15分钟后,甲仓库内快件数量为130件,①错误;对于乙仓库,当x=15时,y=180,当x=60时,y=0,所以乙仓库每分钟派送快件数量为180÷(60-15)=4(件),②正确;设甲仓库的快件数量y关于时间x的函数关系式为y=kx+b(k≠0),当x=0时,y=40,当x=15时,y=130,所以解得所以y=6x+40,8:00时,x=60,当x=60时,y=6×60+40=400,所以8:00时,甲仓库内快件数量为400件,③错误;设乙仓库的快件数量y关于时间x的函数关系式为y=mx+n(m≠0),当x=15时,y=180,当x=60,y=0,所以解得所以y=-4x+240,7:20时,x=20,把x=20代入y=6x+40,得y=6×20+40=160,把x=20代入y=-4x+240,得y=-4×20+240=160,所以7:20时,两仓库快件数量相同,④正确.
三、解答题
18.解析 (1)把(0,0)代入y=(3-m)x+m-5,得m-5=0,解得m=5.
(2)因为一次函数y=(3-m)x+m-5的图象经过第二、三、四象限,所以解得319.解析 (1)设AB所在直线的函数表达式为F拉力=kx+b(k≠0),将(6,4),(10,2.5)代入,得解得∴AB所在直线的函数表达式为F拉力=-x+.
(2)由题图可知G重力=4 N,当6≤x≤10时,F拉力=-x+,
当x=8时,F拉力=-×8+=.∵4-=(N),
∴当石块下降的高度为8 cm时,该石块所受浮力为 N.
20.解析 (1)根据题表中的数据可知,总水量y与时间t为一次函数关系.设y关于t的表达式为y=kt+b(k≠0),∵当t=1时,y=7,当t=2时,y=12,
∴解得
∴y关于t的表达式为y=5t+2.
经验证,题表中其他数据也符合上式.
(2)①当t=20时,y=5×20+2=102,由此估算,小明在第20分钟测量时量筒中的总水量是102毫升.
②对于y=5t+2,当t=0时,y=2,当t=24×60=1 440时,y=5×1 440+2=7 202,=144(天).
答:估算这个水龙头一个月(按30天计)的漏水量可供一人饮用144天.
21.解析 (1)将点C(2,m)代入y1=-x+3,得m=-2+3=1,∴C(2,1).将点C的坐标代入y2=kx-2,得2k-2=1,解得k=.
(2)当x=0时,y1=0+3=3,∴A(0,3).
当x=0时,y2=0-2=-2,∴B(0,-2),∴AB=5,
∴△ABC的面积=×5×2=5.
(3)∵△ABP与△ABC的面积相等,∴AB·|xP|=AB·|xC|,
∴|xP|=|xC|,∵C(2,1),点P不与点C重合,∴点P的横坐标为-2,
∵点P在直线y2上,∴点P的纵坐标为×(-2)-2=-5,
∴点P的坐标为(-2,-5).
22.解析 (1)设A型机器人模型的单价是x元,则B型机器人模型的单价是(x-200)元,根据题意,得=,解这个方程,得x=500,经检验,x=500是原方程的解,且符合题意,∴x-200=300.
答:A型机器人模型的单价是500元,B型机器人模型的单价是300元.
(2)设购买A型机器人模型m台,购买A,B两种型号的机器人模型共花费w元,则购买B型机器人模型(40-m)台,
由题意得w=500×0.8m+300×0.8(40-m)=160m+9 600.
由题意得40-m≤3m,解得m≥10,∵160>0,
∴w随m的增大而增大,∴当m=10时,w取得最小值,最小值为160×10+9 600=11 200,此时40-m=30.
答:购买A型机器人模型10台,B型机器人模型30台时花费最少,最少花费是11 200元.
23.解析 (1)把y=0代入y=-x+4,得0=-x+4,解得x=3,∴点A的坐标为(3,0).把x=0代入y=-x+4,得y=4,∴点B的坐标为(0,4).
(2)如图①,过点C作CE⊥AB于点E,∵点A的坐标为(3,0),点B的坐标为(0,4),∴OA=3,OB=4,∴AB==5.
∵AC平分∠OAB,∴OC=CE.
∵AC=AC,∴Rt△AOC≌Rt△AEC(HL),∴AE=OA=3,∴BE=5-3=2.
设OC=CE=x,则BC=4-x,
在Rt△BCE中,BC2=CE2+BE2,即(4-x)2=x2+22,
解得x=,∴BC=.
(3)存在.如图②,作出符合要求的△ABD,△ABD1,△ABD2,△ABD3,作DF⊥y轴于点F,
由题意得AB=BD,∠ABD=90°,
∵∠ABO=90°-∠DBF=∠BDF,∠AOB=∠BFD=90°,
∴△ABO≌△BDF(AAS),∴DF=OB=4,BF=OA=3,
∴OF=7,∴点D的坐标为(4,7).
同理,点D1的坐标为(-4,1);点D2的坐标为(7,3);点D3的坐标为(-1,-3).综上,点D的坐标为(4,7)或(-4,1)或(7,3)或(-1,-3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学八年级下学期
第10章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共36分)
1.(2023湖南长沙实验教育集团期中)下列函数是正比例函数的是( )
A.y= B.y= C.y=x2+1 D.y=3x+1
2.(2022湖南邵阳中考)在直角坐标系中,已知点A,点B是直线y=kx+b上的两点,则m,n的大小关系是( )
A.m
3.(2022陕西中考)在同一平面直角坐标系中,直线y=-x+4与y=2x+m相交于点P(3,n),则关于x,y的方程组的解为( )
A. B. C. D.
4.(2023四川乐山中考)下列各点在函数y=2x-1图象上的是( )
A.(-1,3) B.(0,1) C.(1,-1) D.(2,3)
5.(2022辽宁抚顺中考)如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图象分别为直线l1和直线l2,下列结论正确的是( )
A.k1·k2<0 B.k1+k2<0
C.b1-b2<0 D.b1·b2<0
6.(2023内蒙古包头中考)在平面直角坐标系中,将正比例函数y=-2x的图象向右平移3个单位长度得到一次函数y=kx+b(k≠0)的图象,则该一次函数的解析式为( )
A.y=-2x+3 B.y=-2x+6
C.y=-2x-3 D.y=-2x-6
7.(2023四川成都七中期中)如图,函数y1=-2x与y2=ax+3的图象相交于点A(m,2),则关于x的不等式-2x>ax+3的解集是( )
A.x>2 B.x<2
C.x>-1 D.x<-1
8.(2023山东聊城高唐期末)如图,点A(-2,6),B(-4,2),当直线y=kx-2(k≠0)与线段AB有交点时,k的取值范围是( )
A.k≤-1 B.k≥-4
C.k≤-4或k≥-1 D.-4≤k≤-1
9.(2021四川资阳中考改编)一对变量满足如图所示的函数关系.设计以下问题情境:①小明从家骑车以600米/分的速度匀速骑了2.5分钟,在原地停留了2分钟,然后以1 000米/分的速度匀速骑回家.设所用时间为x分钟,离家的距离为y千米.②有一个容积为1.5升的开口空瓶子,小张以0.6升/秒的速度匀速向这个瓶子里注水,注满后停止,等2秒后,再以1升/秒的速度匀速倒出瓶子中的水.设所用时间为x秒,瓶子内水的体积为y升.③在矩形ABCD中,AB=1.5,BC=2,点P从点A出发,沿路线AC—CD—DA运动至点A停止.设点P的运动路程为x,△ABP的面积为y.其中,符合图中函数关系的情境个数为( )
A.3 B.2 C.1 D.0
10.在同一平面直角坐标系中,一次函数y=ax+a2与y=a2x+a的图象可能是( )
A B C D
11.(2023河北石家庄外国语教育集团期中)为了节约水资源,自来水公司按分段收费标准收费,下图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.按照分段收费标准,小颖家三、四月份分别交水费29元和19.8元,则四月份比三月份节约用水( )
A.2吨 B.2.5吨
C.3吨 D.3.5吨
12.【山东常考·最值问题】如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
A.(0,0) B. C. D.
二、填空题(每小题3分,共15分)
13.(2023山东滨州阳信期中)已知函数y=(m-2)+6是关于x的一次函数,则m= .
14.(2023山东潍坊临朐期末)某种小汽车加满油箱,且正常行驶时,油箱中的剩余油量Q(升)与行驶里程x(千米)的关系式为Q=45-0.09x.从关系式可知这种小汽车加满油箱最多可以行驶 千米.
15.(2022山东菏泽单县期末)如图,已知直线l1:y=-2x+4与x轴、y轴分别交于A、B两点,那么过原点O且将△AOB的面积平分的直线l2的表达式为 .
16.【新考向·规律探究题】【新独家原创】如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1、l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,……依次进行下去,则点A2 025的坐标为 .
17.(2022山东聊城冠县期末)某快递公司每天上午7:00~8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分钟)之间的函数关系如图所示,下列说法:
①15分钟后,甲仓库内快件数量为180件;
②乙仓库每分钟派送快件数量为4件;
③8:00时,甲仓库内快件数量为600件;
④7:20时,两仓库快件数量相同.
其中正确的是 .(填所有正确说法的序号)
三、解答题(共49分)
18.(2023湖南长沙雅礼教育集团期中)(6分)已知关于x的一次函数y=(3-m)x+m-5.
(1)若一次函数的图象过原点,求实数m的值.
(2)当一次函数的图象经过第二、三、四象限时,求实数m的取值范围.
19.【跨学科·物理】(2022陕西中考)(7分)在测浮力的实验中,将一长方体石块由玻璃器皿的上方,向下缓慢移动浸入水里的过程中,弹簧测力计的示数F拉力(N)与石块下降的高度x(cm)之间的关系如图所示.
(1)求AB所在直线的函数表达式.
(2)当石块下降的高度为8 cm时,求该石块所受浮力的大小.
(温馨提示:当石块位于水面上方时,F拉力=G重力;当石块入水后,F拉力=G重力-F浮力)
20.(2023湖南永州中考)(8分)小明观察到一个水龙头因损坏而不断地滴水,为探究其漏水造成的浪费情况,小明用一个带有刻度的量筒放在水龙头下面装水,每隔一分钟记录量筒中的总水量,但由于操作延误,开始计时的时候量筒中已经有少量水,因而得到如下表所示的一组数据:
时间t(单位:分钟) 1 2 3 4 5 …
总水量y(单位:毫升) 7 12 17 22 27 …
(1)探究:根据上表中的数据,请判断总水量y与时间t的函数关系,并求出y关于t的表达式.
(2)应用:①请你估算小明在第20分钟测量时量筒中的总水量是多少毫升.
②一个人一天大约饮用1 500毫升水,请你估算这个水龙头一个月(按30天计)的漏水量可供一人饮用多少天.
21.(2023山东聊城莘县期末)(8分)直线y1=-x+3和直线y2=kx-2分别交y轴于点A、B,两直线交于点C(2,m).
(1)求m、k的值.
(2)求△ABC的面积.
(3)在直线y2上存在异于点C的另一点P,使得△ABP与△ABC的面积相等,请求出点P的坐标.
22.(2023山东济南中考)(10分)某校开设智能机器人编程的校本课程,购买了A,B两种型号的机器人模型.A型机器人模型单价比B型机器人模型单价多200元,用2 000元购买A型机器人模型和用1 200元购买B型机器人模型的数量相同.
(1)求A,B两种型号的机器人模型的单价分别是多少元.
(2)学校准备再次购买A,B两种型号的机器人模型共40台,购买B型机器人模型不超过A型机器人模型的3倍,且商家给出了两种型号机器人模型均打八折的优惠.问:购买A,B两种型号的机器人模型各多少台时花费最少 最少花费是多少元
23.(2023山西运城实验中学期中)(10分)如图,在平面直角坐标系中,一次函数y=-x+4的图象分别交x轴、y轴于点A、B,点C在y轴上,AC平分∠OAB.
(1)求点A、B的坐标.
(2)求线段BC的长.
(3)在平面直角坐标系中是否存在点D,使得△ABD是以AB为直角边的等腰直角三角形 若存在,请直接写出点D的坐标;若不存在,请说明理由.
答案全解全析
一、选择题
1.A 形如y=kx(k为常数且k≠0)的函数叫做正比例函数,y=是正比例函数,故选A.
2.A 因为k<0,所以一次函数y=kx+b中,y随x的增大而减小,
因为点A,点B是直线y=kx+b(k<0)上的两点,>,
所以m
4.D A.把x=-1代入y=2x-1,得y=2×(-1)-1=-3,∴点(-1,3)不在函数y=2x-1的图象上;B.把x=0代入y=2x-1,得y=2×0-1=-1,∴点(0,1)不在函数y=2x-1的图象上;C.把x=1代入y=2x-1,得y=2×1-1=1,∴点(1,-1)不在函数y=2x-1的图象上;D.把x=2代入y=2x-1,得y=2×2-1=3,∴点(2,3)在函数y=2x-1的图象上.故选D.
5.D ∵一次函数y=k1x+b1的图象经过第一、二、三象限,∴k1>0,b1>0,∵一次函数y=k2x+b2的图象经过第一、三、四象限,∴k2>0,b2<0,所以k1·k2>0,k1+k2>0,b1-b2>0,b1·b2<0.
6.B 正比例函数y=-2x的图象向右平移3个单位长度,得到的一次函数图象的解析式为y=-2(x-3)=-2x+6.
7.D ∵函数y1=-2x的图象过点A(m,2),∴-2m=2,解得m=-1,∴A(-1,2),由题图可知不等式-2x>ax+3的解集为x<-1.
8.D 当直线过点A时,将A(-2,6)代入y=kx-2中,得6=-2k-2,解得k=-4;当直线过点B时,将B(-4,2)代入y=kx-2中,得2=-4k-2,解得k=-1,易知直线y=kx-2与y轴交于点(0,-2),结合题图可知,当直线y=kx-2与线段AB有交点时,k的取值范围为-4≤k≤-1,故选D.
9.B ①小明从家骑车以600米/分的速度匀速骑了2.5分钟,离家的距离为600×2.5=1 500(米)=1.5(千米),原地停留2分钟,2.5+2=4.5(分钟),返回需要的时间为1 500÷1 000=1.5(分钟),4.5+1.5=6(分钟),符合题意;②将瓶子注满水所用的时间为1.5÷0.6=2.5(秒),2.5+2=4.5(秒),倒出瓶子中的水所用时间为1.5÷1=1.5(秒),4.5+1.5=6(秒),符合题意;③根据勾股定理,得AC===2.5,当点P在AC上运动时,y随x的增大而增大,运动到C点时,x=2.5,y=×2×1.5=1.5,当点P在CD上运动时,y=1.5,运动到点D时,x=2.5+1.5=4,当点P在AD上运动时,y随x的增大而减小,结合题图可知,③不符合题意.故选B.
10.D 对于y=ax+a2与y=a2x+a,当x=1时,两函数的值都是a2+a,所以两直线的交点的横坐标为1.①若a>0,则直线y=ax+a2与y=a2x+a都经过第一、二、三象限;②若a<0,则直线y=ax+a2经过第一、二、四象限,直线y=a2x+a经过第一、三、四象限,故选D.
11.C 当0≤x<10时,设y与x的函数关系式为y=mx(m≠0),由题意得22=10m,解得m=2.2,所以y=2.2x.当x≥10时,设y与x的函数关系式为y=kx+b(k≠0),把(10,22)与(20,57)代入y=kx+b,得解得所以y=3.5x-13.综上,y=因为y=29>22,所以x>10,将y=29代入y=3.5x-13,得29=3.5x-13,解得x=12.因为y=19.8<22,所以0≤x<10,将y=19.8代入y=2.2x,得19.8=2.2x,解得x=9,所以四月份比三月份节约用水12-9=3(吨).
12.B 如图,过点A作AB'⊥OB,垂足为点B',由垂线段最短可知,当点B与点B'重合时,AB最短.因为点B'在直线y=x上,所以∠AOB'=45°,因为AB'⊥OB',所以△AOB'是等腰直角三角形.过点B'作B'C⊥x轴,垂足为C,则△B'CO为等腰直角三角形,因为点A的坐标为(-1,0),所以OA=1,所以OC=CB'=OA=×1=,所以点B'的坐标为,故当线段AB最短时,点B的坐标为.
二、填空题
13.答案 -2
解析 ∵函数y=(m-2)+6是关于x的一次函数,
∴m-2≠0且m2-3=1,∴m=-2.
14.答案 500
解析 把Q=0代入Q=45-0.09x,得45-0.09x=0,解得x=500,
即这种小汽车加满油箱最多可以行驶500千米.
15.答案 y=2x
解析 把x=0代入y=-2x+4,得y=4,则B(0,4),把y=0代入y=-2x+4,得-2x+4=0,解得x=2,则A(2,0),所以线段AB的中点的坐标为(1,2).设直线l2的表达式为y=kx(k≠0),把(1,2)代入,得k=2,所以直线l2的表达式为y=2x.
16.答案 (21 012,21 013)
解析 ∵过点(1,0)作x轴的垂线交l1于点A1,∴A1(1,2),把y=2代入y=-x,得x=-2,即A2(-2,2),把x=-2代入y=2x,得y=-4,即A3(-2,-4),同理可得A4(4,-4),A5(4,8),∴点A2n+1(n为自然数)的横坐标为(-2)n,点A2n+1的纵坐标为2×(-2)n.∵2 025=1 012×2+1,∴A2 025的横坐标为(-2)1 012=21 012,纵坐标为2×(-2)1 012=21 013,∴A2 025的坐标为(21 012,21 013).
17.答案 ②④
解析 由图象可知,对于甲仓库,当x=15时,y=130,即15分钟后,甲仓库内快件数量为130件,①错误;对于乙仓库,当x=15时,y=180,当x=60时,y=0,所以乙仓库每分钟派送快件数量为180÷(60-15)=4(件),②正确;设甲仓库的快件数量y关于时间x的函数关系式为y=kx+b(k≠0),当x=0时,y=40,当x=15时,y=130,所以解得所以y=6x+40,8:00时,x=60,当x=60时,y=6×60+40=400,所以8:00时,甲仓库内快件数量为400件,③错误;设乙仓库的快件数量y关于时间x的函数关系式为y=mx+n(m≠0),当x=15时,y=180,当x=60,y=0,所以解得所以y=-4x+240,7:20时,x=20,把x=20代入y=6x+40,得y=6×20+40=160,把x=20代入y=-4x+240,得y=-4×20+240=160,所以7:20时,两仓库快件数量相同,④正确.
三、解答题
18.解析 (1)把(0,0)代入y=(3-m)x+m-5,得m-5=0,解得m=5.
(2)因为一次函数y=(3-m)x+m-5的图象经过第二、三、四象限,所以解得3
(2)由题图可知G重力=4 N,当6≤x≤10时,F拉力=-x+,
当x=8时,F拉力=-×8+=.∵4-=(N),
∴当石块下降的高度为8 cm时,该石块所受浮力为 N.
20.解析 (1)根据题表中的数据可知,总水量y与时间t为一次函数关系.设y关于t的表达式为y=kt+b(k≠0),∵当t=1时,y=7,当t=2时,y=12,
∴解得
∴y关于t的表达式为y=5t+2.
经验证,题表中其他数据也符合上式.
(2)①当t=20时,y=5×20+2=102,由此估算,小明在第20分钟测量时量筒中的总水量是102毫升.
②对于y=5t+2,当t=0时,y=2,当t=24×60=1 440时,y=5×1 440+2=7 202,=144(天).
答:估算这个水龙头一个月(按30天计)的漏水量可供一人饮用144天.
21.解析 (1)将点C(2,m)代入y1=-x+3,得m=-2+3=1,∴C(2,1).将点C的坐标代入y2=kx-2,得2k-2=1,解得k=.
(2)当x=0时,y1=0+3=3,∴A(0,3).
当x=0时,y2=0-2=-2,∴B(0,-2),∴AB=5,
∴△ABC的面积=×5×2=5.
(3)∵△ABP与△ABC的面积相等,∴AB·|xP|=AB·|xC|,
∴|xP|=|xC|,∵C(2,1),点P不与点C重合,∴点P的横坐标为-2,
∵点P在直线y2上,∴点P的纵坐标为×(-2)-2=-5,
∴点P的坐标为(-2,-5).
22.解析 (1)设A型机器人模型的单价是x元,则B型机器人模型的单价是(x-200)元,根据题意,得=,解这个方程,得x=500,经检验,x=500是原方程的解,且符合题意,∴x-200=300.
答:A型机器人模型的单价是500元,B型机器人模型的单价是300元.
(2)设购买A型机器人模型m台,购买A,B两种型号的机器人模型共花费w元,则购买B型机器人模型(40-m)台,
由题意得w=500×0.8m+300×0.8(40-m)=160m+9 600.
由题意得40-m≤3m,解得m≥10,∵160>0,
∴w随m的增大而增大,∴当m=10时,w取得最小值,最小值为160×10+9 600=11 200,此时40-m=30.
答:购买A型机器人模型10台,B型机器人模型30台时花费最少,最少花费是11 200元.
23.解析 (1)把y=0代入y=-x+4,得0=-x+4,解得x=3,∴点A的坐标为(3,0).把x=0代入y=-x+4,得y=4,∴点B的坐标为(0,4).
(2)如图①,过点C作CE⊥AB于点E,∵点A的坐标为(3,0),点B的坐标为(0,4),∴OA=3,OB=4,∴AB==5.
∵AC平分∠OAB,∴OC=CE.
∵AC=AC,∴Rt△AOC≌Rt△AEC(HL),∴AE=OA=3,∴BE=5-3=2.
设OC=CE=x,则BC=4-x,
在Rt△BCE中,BC2=CE2+BE2,即(4-x)2=x2+22,
解得x=,∴BC=.
(3)存在.如图②,作出符合要求的△ABD,△ABD1,△ABD2,△ABD3,作DF⊥y轴于点F,
由题意得AB=BD,∠ABD=90°,
∵∠ABO=90°-∠DBF=∠BDF,∠AOB=∠BFD=90°,
∴△ABO≌△BDF(AAS),∴DF=OB=4,BF=OA=3,
∴OF=7,∴点D的坐标为(4,7).
同理,点D1的坐标为(-4,1);点D2的坐标为(7,3);点D3的坐标为(-1,-3).综上,点D的坐标为(4,7)或(-4,1)或(7,3)或(-1,-3).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
