2024青岛版数学八年级下学期--第11章《图形的平移与旋转》素养综合检测(含解析)
文档属性
| 名称 | 2024青岛版数学八年级下学期--第11章《图形的平移与旋转》素养综合检测(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 616.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024青岛版数学八年级下学期
第11章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共36分)
1.(2023广东清远清新二中期中)下列运动属于平移的是( )
A.空中放飞的风筝
B.飞机在跑道上直线滑行
C.篮球被运动员投出后进入篮筐的过程
D.乒乓球比赛中,乒乓球的运动
2.【中华优秀传统文化】(2023山东日照中考)窗花是贴在窗户上的剪纸,是中国的传统民间艺术之一.下列窗花作品既是轴对称图形又是中心对称图形的是( )
3.(2023四川凉山州中考)点P(2,-3)关于原点对称的点P'的坐标是( )
A.(2,3) B.(-2,-3) C.(-3,2) D.(-2,3)
4.(2022山东聊城阳谷期末)如图,△ABC中,∠ABC=∠ACB=75°,将△ABC绕点C旋转(旋转角大于0°,且小于360°),得到△DEC,点A的对应点D在BC的延长线上,则旋转方向和旋转角可能为( )
A.逆时针,30° B.逆时针,105° C.顺时针,30° D.顺时针,105°
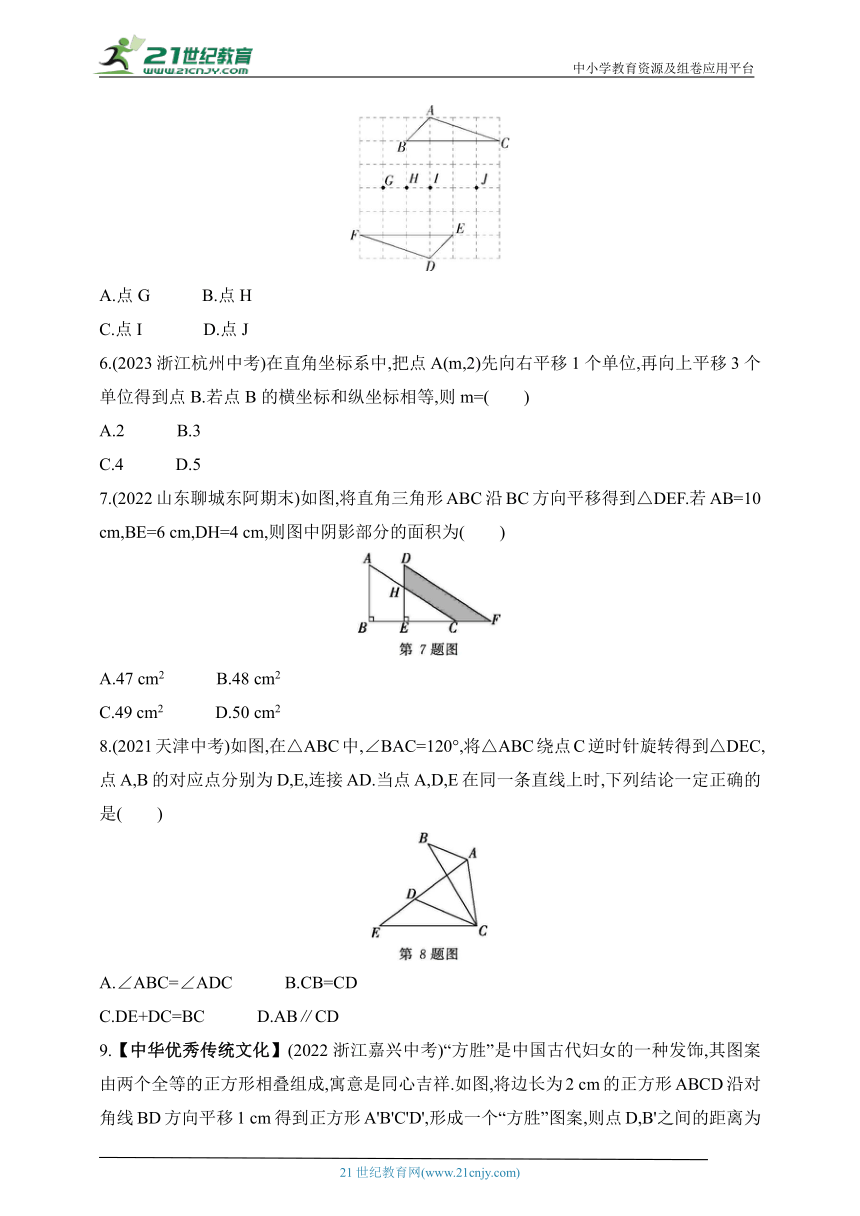
5.【教材变式·P189T1】(2023北京大兴一模)如图,在正方形网格中,A,B,C,D,E,F,G,H,I,J是网格线交点,△ABC与△DEF关于某点成中心对称,则其对称中心是( )
A.点G B.点H
C.点I D.点J
6.(2023浙江杭州中考)在直角坐标系中,把点A(m,2)先向右平移1个单位,再向上平移3个单位得到点B.若点B的横坐标和纵坐标相等,则m=( )
A.2 B.3
C.4 D.5
7.(2022山东聊城东阿期末)如图,将直角三角形ABC沿BC方向平移得到△DEF.若AB=10 cm,BE=6 cm,DH=4 cm,则图中阴影部分的面积为( )
A.47 cm2 B.48 cm2
C.49 cm2 D.50 cm2
8.(2021天津中考)如图,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,下列结论一定正确的是( )
A.∠ABC=∠ADC B.CB=CD
C.DE+DC=BC D.AB∥CD
9.【中华优秀传统文化】(2022浙江嘉兴中考)“方胜”是中国古代妇女的一种发饰,其图案由两个全等的正方形相叠组成,寓意是同心吉祥.如图,将边长为2 cm的正方形ABCD沿对角线BD方向平移1 cm得到正方形A'B'C'D',形成一个“方胜”图案,则点D,B'之间的距离为( )
A.1 cm B.2 cm
C.(-1)cm D.(2-1)cm
10.【山东常考·最值问题】(2021山东菏泽单县期末)如图,Rt△ABC中,∠ACB=90°,AB=5,BC=3,点D是斜边上任意一点,将点D绕点C逆时针旋转60°得到点E,连接CD,DE,CE,则线段DE长度的最小值为 ( )
A. B. C. D.3
11.把一副三角板按如图①所示的方式放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°到△D1CE1的位置(如图②),则AD1的长为( )
A.3 B.5
C.4 D.
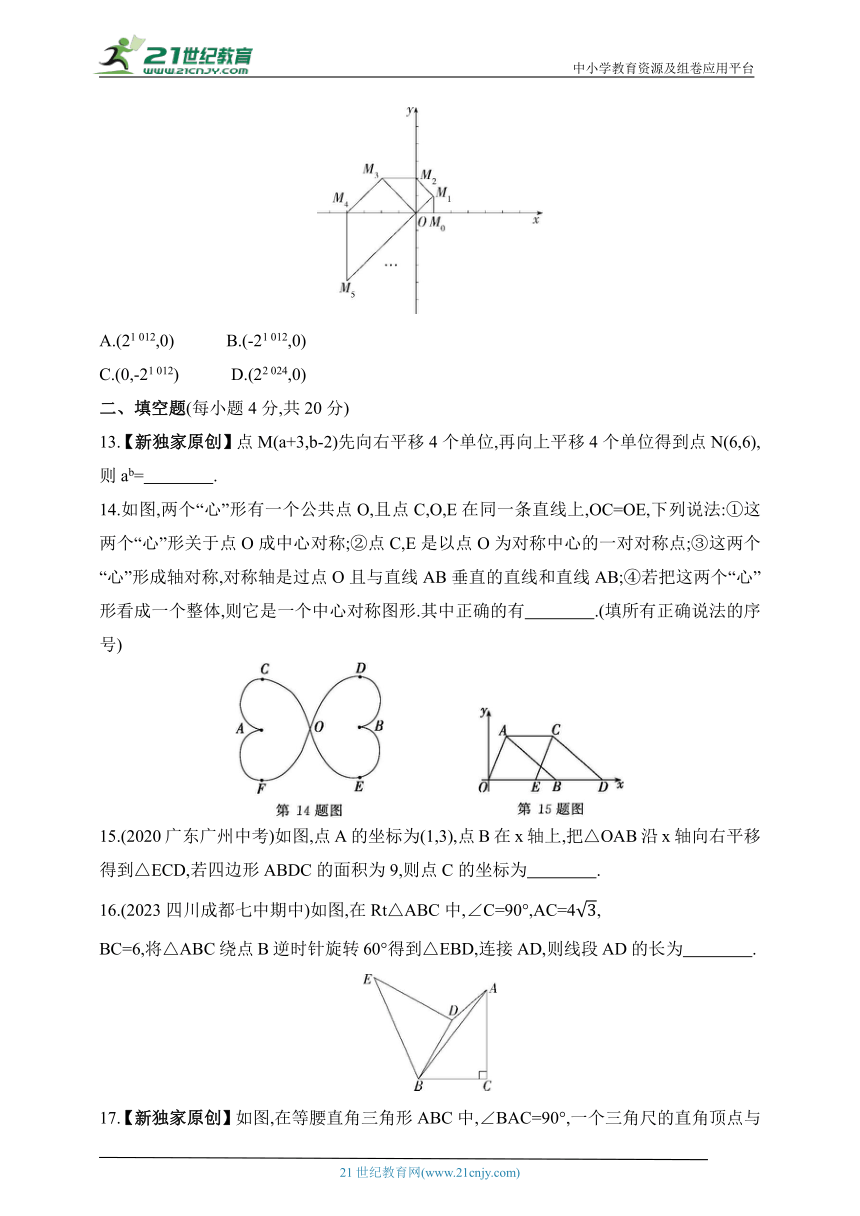
12.【新考向·规律探究题】(2022山东聊城冠县期末改编)如图,在平面直角坐标系中,已知点M0的坐标为(1,0),将线段OM0绕原点O逆时针旋转45°,再将其延长到M1,使得M1M0⊥OM0,得到线段OM1;又将线段OM1绕原点O逆时针旋转45°,再将其延长到M2,使得M2M1⊥OM1,得到线段OM2;如此下去,得到线段OM3,OM4,OM5,…….根据以上规律,点M2 024的坐标为( )
A.(21 012,0) B.(-21 012,0)
C.(0,-21 012) D.(22 024,0)
二、填空题(每小题4分,共20分)
13.【新独家原创】点M(a+3,b-2)先向右平移4个单位,再向上平移4个单位得到点N(6,6),则ab= .
14.如图,两个“心”形有一个公共点O,且点C,O,E在同一条直线上,OC=OE,下列说法:①这两个“心”形关于点O成中心对称;②点C,E是以点O为对称中心的一对对称点;③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB;④若把这两个“心”形看成一个整体,则它是一个中心对称图形.其中正确的有 .(填所有正确说法的序号)
15.(2020广东广州中考)如图,点A的坐标为(1,3),点B在x轴上,把△OAB沿x轴向右平移得到△ECD,若四边形ABDC的面积为9,则点C的坐标为 .
16.(2023四川成都七中期中)如图,在Rt△ABC中,∠C=90°,AC=4,
BC=6,将△ABC绕点B逆时针旋转60°得到△EBD,连接AD,则线段AD的长为 .
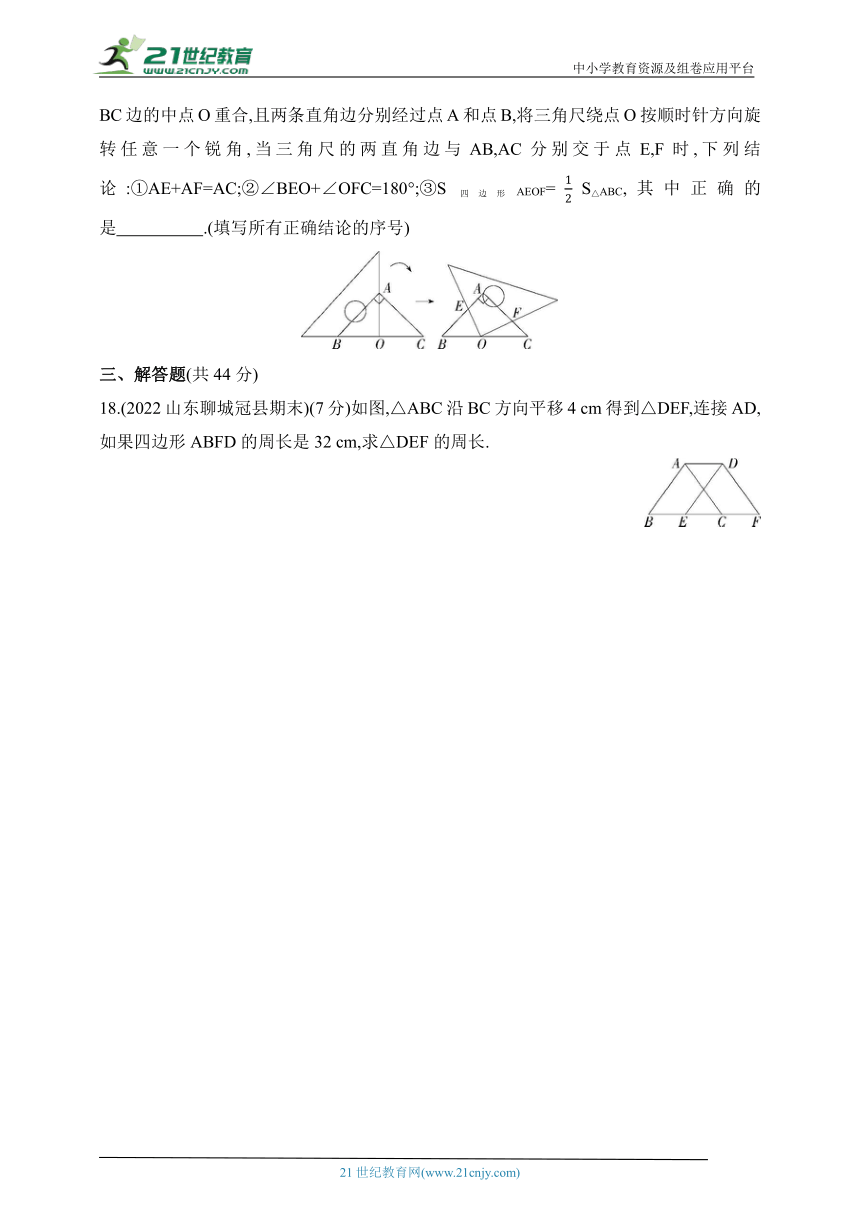
17.【新独家原创】如图,在等腰直角三角形ABC中,∠BAC=90°,一个三角尺的直角顶点与BC边的中点O重合,且两条直角边分别经过点A和点B,将三角尺绕点O按顺时针方向旋转任意一个锐角,当三角尺的两直角边与AB,AC分别交于点E,F时,下列结论:①AE+AF=AC;②∠BEO+∠OFC=180°;③S四边形AEOF=S△ABC,其中正确的是 .(填写所有正确结论的序号)
三、解答题(共44分)
18.(2022山东聊城冠县期末)(7分)如图,△ABC沿BC方向平移4 cm得到△DEF,连接AD,如果四边形ABFD的周长是32 cm,求△DEF的周长.
19.(2023山东潍坊高新区期末)(8分)如图,在方格纸(每个小正方形的边长都是1个单位长度)中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,已知A(0,2),B(2,2),C(1,1).
(1)将△ABC先向左平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,请画出△A1B1C1,并写出点C1的坐标.
(2)△ABC与△A2B2C2关于原点O成中心对称,请画出△A2B2C2,写出点B2的坐标.
(3)将△ABC绕点P按顺时针方向旋转90°后得到△A3B3C3,请直接写出点P的坐标.
20.(2021湖南湘西州中考)(9分)如图,在△ABC中,点D在AB边上,CB=CD,将边CA绕点C旋转到CE的位置,使得∠ECA=∠DCB,连接DE,与AC交于点F,∠B=70°,∠A=10°.
(1)求证:AB=ED.
(2)求∠AFE的度数.
21.【新考法】(2023山东潍坊安丘期末)(10分)材料:“八年级下册课本第187页例2:如图,ABCD是一块正方形的土地,要在这块土地上修建两条笔直的、互相垂直的小路,把这块土地分成面积相等的四部分.你有哪些不同的方案 画出图形,并说明理由.”
方案如下:(理由略)
小亮在学习了上述解决方案后,发现三种分割方案的图形都是中心对称图形.这为他创作数学社团图标提供了灵感.经过思考,小亮设计了一个中心对称图形的社团图标,如下图所示.已知O为正方形ABCD的对称中心,EF为☉O的直径,连接BE,DF.
(1)请你说明此图标是中心对称图形.
(2)若DF⊥EF,则AD,DF,EF三者满足DF2+EF2=AD2.请证明此结论.
22.(2023山东菏泽定陶期末)(10分)
(1)如图①,已知正方形ABCD,点E,F分别在边BC,AB上,且BE=BF.此时AF与CE有怎样的数量关系
(2)如图②,△BEF绕点B顺时针旋转α,当0°<α<90°时,连接AF,CE,此时(1)中的AF与CE的数量关系是否仍然成立 如果成立,请说明理由;否则,请举出反例.
(3)如图③,当α=90°时,连接AF,CE.猜想AB与BE有什么数量关系时,直线AF是线段EC的垂直平分线,试说明理由.
答案全解全析
一、选择题
1.B 选项A,空中放飞的风筝飞行的角度不断变化,不是平移;选项B,飞机在跑道上直线滑行,符合平移的定义,是平移;选项C和D,篮球和乒乓球是在旋转中前进,不是平移.
2.A
3.D 点P(x,y)关于原点的对称点的坐标是(-x,-y),所以点P(2,-3)关于原点对称的点P'的坐标是(-2,3).
4.D 由题意可知∠ACD=180°-∠ACB=105°,360°-105°=255°,所以旋转方向和旋转角为顺时针,105°或逆时针,255°.
5.C ∵△ABC与△DEF关于某点成中心对称,∴对应点B和E的连线与对应点C和F的连线的交点I是对称中心.
6.C 把点A(m,2)先向右平移1个单位,再向上平移3个单位得到点B,∴B(m+1,5).∵点B的横坐标和纵坐标相等,∴m+1=5,解得m=4.
7.B 由题意可知△ABC≌△DEF,DE=AB=10 cm,
所以S△ABC=S△DEF,HE=DE-DH=10-4=6(cm),
所以S梯形ABEH+S△CEH=S△CEH+S阴影部分,
所以S阴影部分=S梯形ABEH=×(6+10)×6=48(cm2).
8.D 由题意得CD=CA,∠EDC=∠CAB=120°,因为点A,D,E在同一条直线上,所以∠ADC=60°,所以△ADC为等边三角形,所以∠DAC=60°,所以∠BAD=∠BAC-∠DAC=60°,所以∠BAD=∠ADC,所以AB∥CD,故选D.
9.D 因为四边形ABCD是边长为2 cm的正方形,所以∠A=90°,AB=AD=2 cm,所以BD==2(cm),由平移的性质可知,BB'=1 cm,所以B'D=BD-BB'=(2-1)cm,故选D.
10.A 在Rt△ABC中,AC===4.由旋转的性质,得CD=CE,∠DCE=60°,所以△CDE为等边三角形,所以CD=CE=DE,当CD的值最小时,DE的值最小,易知当CD⊥AB时,CD的值最小,此时S△ABC=AC·BC=AB·CD,即×4×3=×5CD,所以CD=,所以线段DE长度的最小值是.
11.B ∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°-30°=60°,∴∠ACD=90°-60°=30°.
∵旋转角的度数为15°,∴∠ACD1=30°+15°=45°.
设AB与CD1交于点O,
∵∠OAC=45°,∴∠OAC=∠OCA,∠AOC=90°,∴AO=CO,∴△ACO是等腰直角三角形,易知CO=AO=AB=×6=3,
∵D1C=DC=7,∴D1O=7-3=4,
在Rt△AOD1中,AD1===5.故选B.
12.A 因为点M0的坐标为(1,0),所以OM0=1,
因为∠M1OM0=45°,M1M0⊥OM0,所以△OM0M1是等腰直角三角形,
所以M1M0=OM0=1,所以OM1==,
同理,OM2=OM1=()2,OM3=OM2=()3,……,所以OMn=()n,所以OM2 024=()2 024=21 012.
因为旋转8次循环一周,2 024÷8=253,
所以点M2 024在x轴的正半轴上,所以M2 024(21 012,0),故选A.
二、填空题
13.答案 1
解析 因为点M(a+3,b-2)先向右平移4个单位,再向上平移4个单位,得到点(a+3+4,b-2+4),即(a+7,b+2),所以a+7=6,b+2=6,解得a=-1,b=4,所以ab=(-1)4=1.
14.答案 ②
解析 因为点C,O,E在同一条直线上,OC=OE,
所以点C,E是以点O为对称中心的一对对称点,②说法正确;
其他说法不一定正确.
15.答案 (4,3)
解析 设点C的坐标为(a,b).
∵把△OAB沿x轴向右平移得到△ECD,
∴AC=BD,AC∥BD,
∴四边形ABDC是平行四边形,点A和点C的纵坐标相同,∴b=3.
∵四边形ABDC的面积为9,点A的坐标为(1,3),
∴3(a-1)=9,∴a=4,∴点C的坐标为(4,3).
16.答案 2
解析 如图,连接CD,过D作DF⊥AC于F.∵△ABC绕点B逆时针旋转60°得到△EBD,∴△ABC≌△EBD,∠DBC=60°,∴BC=BD,
∴△DBC为等边三角形,∴CD=CB=6,∠DCB=60°.
∵∠ACB=90°,∴∠DCF=30°.
∴在Rt△DCF中,DF=CD=3,∴CF===3.
∵AC=4,∴AF=AC-CF=.在Rt△ADF中,AD==2.
17.答案 ①②③
解析 连接AO,如图.
∵△ABC为等腰直角三角形,∠BAC=90°,∴AB=AC,∠B=∠C=45°.
又∵点O为BC的中点,
∴∠AOB=∠AOC=90°,OA=BC=OB=OC,∠BAO=∠CAO=∠BAC=45°,∴∠BAO=∠C.∵∠EOA+∠AOF=∠EOF=90°,∠AOF+∠FOC=
∠AOC=90°,∴∠EOA=∠FOC.
在△EOA和△FOC中,∴△EOA≌△FOC(ASA),
∴EA=FC,∴AE+AF=FC+AF=AC,结论①正确;
∵△EOA≌△FOC,∴∠AEO=∠CFO,
∴∠BEO+∠CFO=∠BEO+∠AEO=180°,结论②正确;
∵△EOA≌△FOC,∴S△EOA=S△FOC,
∴S四边形AEOF=S△EOA+S△AOF=S△FOC+S△AOF=S△AOC=S△ABC,结论③正确.
三、解答题
18.解析 因为△ABC沿BC方向平移4 cm得到△DEF,
所以△ABC≌△DEF,AC=DF,AD=CF=4 cm,
因为四边形ABFD的周长是32 cm,
所以AB+BC+CF+DF+AD=32 cm,
即AB+BC+CF+AC+DA=32 cm,
所以AB+BC+AC=24 cm,
所以△ABC的周长为24 cm,
所以△DEF的周长是24 cm.
19.解析 (1)如图所示,△A1B1C1即为所求,点C1的坐标为(-3,0).
(2)如图所示,△A2B2C2即为所求,点B2的坐标为(-2,-2).
(3)如图,点P的坐标是(-2,0).
20.解析 (1)证明:因为∠ECA=∠DCB,
所以∠ECA+∠ACD=∠DCB+∠ACD,即∠ECD=∠BCA.
由旋转的性质可得CA=CE,
在△BCA和△DCE中,
所以△BCA≌△DCE(SAS),所以AB=ED.
(2)因为△BCA≌△DCE,所以∠CDE=∠B=70°,因为CB=CD,所以∠CDB=∠B=70°,所以∠EDA=180°-∠CDE-∠CDB=180°-70°-70°=40°,所以∠AFE=∠EDA+∠A=40°+10°=50°.
21.证明 (1)∵正方形ABCD、☉O、直径EF都是中心对称图形且对称中心均为点O,∴点D和点B关于点O成中心对称,点E和点F关于点O成中心对称,∴DF和BE关于点O成中心对称,∴由正方形ABCD、☉O、直径EF、线段DF和BE组成的图标是以点O为对称中心的中心对称图形.
(2)如图,连接BD,易知点O在BD上,OF=EF,OD=BD.
∵四边形ABCD为正方形,∴BD==AD,∴OD=AD.
∵DF⊥EF,∴在Rt△DFO中,DF2+OF2=OD2,
∴DF2+=,
∴DF2+EF2=AD2.
22.解析 (1)AF与CE的数量关系:AF=CE,
理由:∵四边形ABCD是正方形,∴BA=BC,∵BE=BF,
∴BA-BF=BC-BE,∴AF=CE.
(2)AF=CE仍然成立,理由如下:
∵四边形ABCD是正方形,∴AB=CB,∠ABC=∠EBF=90°,
∴∠ABF+∠CBF=∠CBE+∠CBF=90°,∴∠ABF=∠CBE.
在△ABF和△CBE中,,
∴△ABF≌△CBE(SAS),∴AF=CE.
(3)当AB=(+1)BE时,直线AF是线段EC的垂直平分线,理由如下:连接AC,如图,
当α=90°时,点F落在BC边上,∵∠ABC=∠EBF=90°,
∴A、B、E三点共线.
∵四边形ABCD是正方形,∴AC=AB.
∵AB=(+1)BE,∴BE=(-1)AB,∴AE=AB+BE=AB,∴AE=AC,∴点A在线段EC的垂直平分线上.
在Rt△BEF中,∵BE=BF=(-1)AB,∴EF=(2-)AB,
∵BC=AB,∴CF=BC-BF=(2-)AB,∴EF=CF,∴点F在线段EC的垂直平分线上,∴直线AF是线段EC的垂直平分线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学八年级下学期
第11章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共36分)
1.(2023广东清远清新二中期中)下列运动属于平移的是( )
A.空中放飞的风筝
B.飞机在跑道上直线滑行
C.篮球被运动员投出后进入篮筐的过程
D.乒乓球比赛中,乒乓球的运动
2.【中华优秀传统文化】(2023山东日照中考)窗花是贴在窗户上的剪纸,是中国的传统民间艺术之一.下列窗花作品既是轴对称图形又是中心对称图形的是( )
3.(2023四川凉山州中考)点P(2,-3)关于原点对称的点P'的坐标是( )
A.(2,3) B.(-2,-3) C.(-3,2) D.(-2,3)
4.(2022山东聊城阳谷期末)如图,△ABC中,∠ABC=∠ACB=75°,将△ABC绕点C旋转(旋转角大于0°,且小于360°),得到△DEC,点A的对应点D在BC的延长线上,则旋转方向和旋转角可能为( )
A.逆时针,30° B.逆时针,105° C.顺时针,30° D.顺时针,105°
5.【教材变式·P189T1】(2023北京大兴一模)如图,在正方形网格中,A,B,C,D,E,F,G,H,I,J是网格线交点,△ABC与△DEF关于某点成中心对称,则其对称中心是( )
A.点G B.点H
C.点I D.点J
6.(2023浙江杭州中考)在直角坐标系中,把点A(m,2)先向右平移1个单位,再向上平移3个单位得到点B.若点B的横坐标和纵坐标相等,则m=( )
A.2 B.3
C.4 D.5
7.(2022山东聊城东阿期末)如图,将直角三角形ABC沿BC方向平移得到△DEF.若AB=10 cm,BE=6 cm,DH=4 cm,则图中阴影部分的面积为( )
A.47 cm2 B.48 cm2
C.49 cm2 D.50 cm2
8.(2021天津中考)如图,在△ABC中,∠BAC=120°,将△ABC绕点C逆时针旋转得到△DEC,点A,B的对应点分别为D,E,连接AD.当点A,D,E在同一条直线上时,下列结论一定正确的是( )
A.∠ABC=∠ADC B.CB=CD
C.DE+DC=BC D.AB∥CD
9.【中华优秀传统文化】(2022浙江嘉兴中考)“方胜”是中国古代妇女的一种发饰,其图案由两个全等的正方形相叠组成,寓意是同心吉祥.如图,将边长为2 cm的正方形ABCD沿对角线BD方向平移1 cm得到正方形A'B'C'D',形成一个“方胜”图案,则点D,B'之间的距离为( )
A.1 cm B.2 cm
C.(-1)cm D.(2-1)cm
10.【山东常考·最值问题】(2021山东菏泽单县期末)如图,Rt△ABC中,∠ACB=90°,AB=5,BC=3,点D是斜边上任意一点,将点D绕点C逆时针旋转60°得到点E,连接CD,DE,CE,则线段DE长度的最小值为 ( )
A. B. C. D.3
11.把一副三角板按如图①所示的方式放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°到△D1CE1的位置(如图②),则AD1的长为( )
A.3 B.5
C.4 D.
12.【新考向·规律探究题】(2022山东聊城冠县期末改编)如图,在平面直角坐标系中,已知点M0的坐标为(1,0),将线段OM0绕原点O逆时针旋转45°,再将其延长到M1,使得M1M0⊥OM0,得到线段OM1;又将线段OM1绕原点O逆时针旋转45°,再将其延长到M2,使得M2M1⊥OM1,得到线段OM2;如此下去,得到线段OM3,OM4,OM5,…….根据以上规律,点M2 024的坐标为( )
A.(21 012,0) B.(-21 012,0)
C.(0,-21 012) D.(22 024,0)
二、填空题(每小题4分,共20分)
13.【新独家原创】点M(a+3,b-2)先向右平移4个单位,再向上平移4个单位得到点N(6,6),则ab= .
14.如图,两个“心”形有一个公共点O,且点C,O,E在同一条直线上,OC=OE,下列说法:①这两个“心”形关于点O成中心对称;②点C,E是以点O为对称中心的一对对称点;③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB;④若把这两个“心”形看成一个整体,则它是一个中心对称图形.其中正确的有 .(填所有正确说法的序号)
15.(2020广东广州中考)如图,点A的坐标为(1,3),点B在x轴上,把△OAB沿x轴向右平移得到△ECD,若四边形ABDC的面积为9,则点C的坐标为 .
16.(2023四川成都七中期中)如图,在Rt△ABC中,∠C=90°,AC=4,
BC=6,将△ABC绕点B逆时针旋转60°得到△EBD,连接AD,则线段AD的长为 .
17.【新独家原创】如图,在等腰直角三角形ABC中,∠BAC=90°,一个三角尺的直角顶点与BC边的中点O重合,且两条直角边分别经过点A和点B,将三角尺绕点O按顺时针方向旋转任意一个锐角,当三角尺的两直角边与AB,AC分别交于点E,F时,下列结论:①AE+AF=AC;②∠BEO+∠OFC=180°;③S四边形AEOF=S△ABC,其中正确的是 .(填写所有正确结论的序号)
三、解答题(共44分)
18.(2022山东聊城冠县期末)(7分)如图,△ABC沿BC方向平移4 cm得到△DEF,连接AD,如果四边形ABFD的周长是32 cm,求△DEF的周长.
19.(2023山东潍坊高新区期末)(8分)如图,在方格纸(每个小正方形的边长都是1个单位长度)中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,已知A(0,2),B(2,2),C(1,1).
(1)将△ABC先向左平移4个单位长度,再向下平移1个单位长度,得到△A1B1C1,请画出△A1B1C1,并写出点C1的坐标.
(2)△ABC与△A2B2C2关于原点O成中心对称,请画出△A2B2C2,写出点B2的坐标.
(3)将△ABC绕点P按顺时针方向旋转90°后得到△A3B3C3,请直接写出点P的坐标.
20.(2021湖南湘西州中考)(9分)如图,在△ABC中,点D在AB边上,CB=CD,将边CA绕点C旋转到CE的位置,使得∠ECA=∠DCB,连接DE,与AC交于点F,∠B=70°,∠A=10°.
(1)求证:AB=ED.
(2)求∠AFE的度数.
21.【新考法】(2023山东潍坊安丘期末)(10分)材料:“八年级下册课本第187页例2:如图,ABCD是一块正方形的土地,要在这块土地上修建两条笔直的、互相垂直的小路,把这块土地分成面积相等的四部分.你有哪些不同的方案 画出图形,并说明理由.”
方案如下:(理由略)
小亮在学习了上述解决方案后,发现三种分割方案的图形都是中心对称图形.这为他创作数学社团图标提供了灵感.经过思考,小亮设计了一个中心对称图形的社团图标,如下图所示.已知O为正方形ABCD的对称中心,EF为☉O的直径,连接BE,DF.
(1)请你说明此图标是中心对称图形.
(2)若DF⊥EF,则AD,DF,EF三者满足DF2+EF2=AD2.请证明此结论.
22.(2023山东菏泽定陶期末)(10分)
(1)如图①,已知正方形ABCD,点E,F分别在边BC,AB上,且BE=BF.此时AF与CE有怎样的数量关系
(2)如图②,△BEF绕点B顺时针旋转α,当0°<α<90°时,连接AF,CE,此时(1)中的AF与CE的数量关系是否仍然成立 如果成立,请说明理由;否则,请举出反例.
(3)如图③,当α=90°时,连接AF,CE.猜想AB与BE有什么数量关系时,直线AF是线段EC的垂直平分线,试说明理由.
答案全解全析
一、选择题
1.B 选项A,空中放飞的风筝飞行的角度不断变化,不是平移;选项B,飞机在跑道上直线滑行,符合平移的定义,是平移;选项C和D,篮球和乒乓球是在旋转中前进,不是平移.
2.A
3.D 点P(x,y)关于原点的对称点的坐标是(-x,-y),所以点P(2,-3)关于原点对称的点P'的坐标是(-2,3).
4.D 由题意可知∠ACD=180°-∠ACB=105°,360°-105°=255°,所以旋转方向和旋转角为顺时针,105°或逆时针,255°.
5.C ∵△ABC与△DEF关于某点成中心对称,∴对应点B和E的连线与对应点C和F的连线的交点I是对称中心.
6.C 把点A(m,2)先向右平移1个单位,再向上平移3个单位得到点B,∴B(m+1,5).∵点B的横坐标和纵坐标相等,∴m+1=5,解得m=4.
7.B 由题意可知△ABC≌△DEF,DE=AB=10 cm,
所以S△ABC=S△DEF,HE=DE-DH=10-4=6(cm),
所以S梯形ABEH+S△CEH=S△CEH+S阴影部分,
所以S阴影部分=S梯形ABEH=×(6+10)×6=48(cm2).
8.D 由题意得CD=CA,∠EDC=∠CAB=120°,因为点A,D,E在同一条直线上,所以∠ADC=60°,所以△ADC为等边三角形,所以∠DAC=60°,所以∠BAD=∠BAC-∠DAC=60°,所以∠BAD=∠ADC,所以AB∥CD,故选D.
9.D 因为四边形ABCD是边长为2 cm的正方形,所以∠A=90°,AB=AD=2 cm,所以BD==2(cm),由平移的性质可知,BB'=1 cm,所以B'D=BD-BB'=(2-1)cm,故选D.
10.A 在Rt△ABC中,AC===4.由旋转的性质,得CD=CE,∠DCE=60°,所以△CDE为等边三角形,所以CD=CE=DE,当CD的值最小时,DE的值最小,易知当CD⊥AB时,CD的值最小,此时S△ABC=AC·BC=AB·CD,即×4×3=×5CD,所以CD=,所以线段DE长度的最小值是.
11.B ∵∠ACB=∠DEC=90°,∠D=30°,
∴∠DCE=90°-30°=60°,∴∠ACD=90°-60°=30°.
∵旋转角的度数为15°,∴∠ACD1=30°+15°=45°.
设AB与CD1交于点O,
∵∠OAC=45°,∴∠OAC=∠OCA,∠AOC=90°,∴AO=CO,∴△ACO是等腰直角三角形,易知CO=AO=AB=×6=3,
∵D1C=DC=7,∴D1O=7-3=4,
在Rt△AOD1中,AD1===5.故选B.
12.A 因为点M0的坐标为(1,0),所以OM0=1,
因为∠M1OM0=45°,M1M0⊥OM0,所以△OM0M1是等腰直角三角形,
所以M1M0=OM0=1,所以OM1==,
同理,OM2=OM1=()2,OM3=OM2=()3,……,所以OMn=()n,所以OM2 024=()2 024=21 012.
因为旋转8次循环一周,2 024÷8=253,
所以点M2 024在x轴的正半轴上,所以M2 024(21 012,0),故选A.
二、填空题
13.答案 1
解析 因为点M(a+3,b-2)先向右平移4个单位,再向上平移4个单位,得到点(a+3+4,b-2+4),即(a+7,b+2),所以a+7=6,b+2=6,解得a=-1,b=4,所以ab=(-1)4=1.
14.答案 ②
解析 因为点C,O,E在同一条直线上,OC=OE,
所以点C,E是以点O为对称中心的一对对称点,②说法正确;
其他说法不一定正确.
15.答案 (4,3)
解析 设点C的坐标为(a,b).
∵把△OAB沿x轴向右平移得到△ECD,
∴AC=BD,AC∥BD,
∴四边形ABDC是平行四边形,点A和点C的纵坐标相同,∴b=3.
∵四边形ABDC的面积为9,点A的坐标为(1,3),
∴3(a-1)=9,∴a=4,∴点C的坐标为(4,3).
16.答案 2
解析 如图,连接CD,过D作DF⊥AC于F.∵△ABC绕点B逆时针旋转60°得到△EBD,∴△ABC≌△EBD,∠DBC=60°,∴BC=BD,
∴△DBC为等边三角形,∴CD=CB=6,∠DCB=60°.
∵∠ACB=90°,∴∠DCF=30°.
∴在Rt△DCF中,DF=CD=3,∴CF===3.
∵AC=4,∴AF=AC-CF=.在Rt△ADF中,AD==2.
17.答案 ①②③
解析 连接AO,如图.
∵△ABC为等腰直角三角形,∠BAC=90°,∴AB=AC,∠B=∠C=45°.
又∵点O为BC的中点,
∴∠AOB=∠AOC=90°,OA=BC=OB=OC,∠BAO=∠CAO=∠BAC=45°,∴∠BAO=∠C.∵∠EOA+∠AOF=∠EOF=90°,∠AOF+∠FOC=
∠AOC=90°,∴∠EOA=∠FOC.
在△EOA和△FOC中,∴△EOA≌△FOC(ASA),
∴EA=FC,∴AE+AF=FC+AF=AC,结论①正确;
∵△EOA≌△FOC,∴∠AEO=∠CFO,
∴∠BEO+∠CFO=∠BEO+∠AEO=180°,结论②正确;
∵△EOA≌△FOC,∴S△EOA=S△FOC,
∴S四边形AEOF=S△EOA+S△AOF=S△FOC+S△AOF=S△AOC=S△ABC,结论③正确.
三、解答题
18.解析 因为△ABC沿BC方向平移4 cm得到△DEF,
所以△ABC≌△DEF,AC=DF,AD=CF=4 cm,
因为四边形ABFD的周长是32 cm,
所以AB+BC+CF+DF+AD=32 cm,
即AB+BC+CF+AC+DA=32 cm,
所以AB+BC+AC=24 cm,
所以△ABC的周长为24 cm,
所以△DEF的周长是24 cm.
19.解析 (1)如图所示,△A1B1C1即为所求,点C1的坐标为(-3,0).
(2)如图所示,△A2B2C2即为所求,点B2的坐标为(-2,-2).
(3)如图,点P的坐标是(-2,0).
20.解析 (1)证明:因为∠ECA=∠DCB,
所以∠ECA+∠ACD=∠DCB+∠ACD,即∠ECD=∠BCA.
由旋转的性质可得CA=CE,
在△BCA和△DCE中,
所以△BCA≌△DCE(SAS),所以AB=ED.
(2)因为△BCA≌△DCE,所以∠CDE=∠B=70°,因为CB=CD,所以∠CDB=∠B=70°,所以∠EDA=180°-∠CDE-∠CDB=180°-70°-70°=40°,所以∠AFE=∠EDA+∠A=40°+10°=50°.
21.证明 (1)∵正方形ABCD、☉O、直径EF都是中心对称图形且对称中心均为点O,∴点D和点B关于点O成中心对称,点E和点F关于点O成中心对称,∴DF和BE关于点O成中心对称,∴由正方形ABCD、☉O、直径EF、线段DF和BE组成的图标是以点O为对称中心的中心对称图形.
(2)如图,连接BD,易知点O在BD上,OF=EF,OD=BD.
∵四边形ABCD为正方形,∴BD==AD,∴OD=AD.
∵DF⊥EF,∴在Rt△DFO中,DF2+OF2=OD2,
∴DF2+=,
∴DF2+EF2=AD2.
22.解析 (1)AF与CE的数量关系:AF=CE,
理由:∵四边形ABCD是正方形,∴BA=BC,∵BE=BF,
∴BA-BF=BC-BE,∴AF=CE.
(2)AF=CE仍然成立,理由如下:
∵四边形ABCD是正方形,∴AB=CB,∠ABC=∠EBF=90°,
∴∠ABF+∠CBF=∠CBE+∠CBF=90°,∴∠ABF=∠CBE.
在△ABF和△CBE中,,
∴△ABF≌△CBE(SAS),∴AF=CE.
(3)当AB=(+1)BE时,直线AF是线段EC的垂直平分线,理由如下:连接AC,如图,
当α=90°时,点F落在BC边上,∵∠ABC=∠EBF=90°,
∴A、B、E三点共线.
∵四边形ABCD是正方形,∴AC=AB.
∵AB=(+1)BE,∴BE=(-1)AB,∴AE=AB+BE=AB,∴AE=AC,∴点A在线段EC的垂直平分线上.
在Rt△BEF中,∵BE=BF=(-1)AB,∴EF=(2-)AB,
∵BC=AB,∴CF=BC-BF=(2-)AB,∴EF=CF,∴点F在线段EC的垂直平分线上,∴直线AF是线段EC的垂直平分线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
