2024青岛版数学八年级下学期--期末素养综合测试(一)(含解析)
文档属性
| 名称 | 2024青岛版数学八年级下学期--期末素养综合测试(一)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 621.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024青岛版数学八年级下学期
期末素养综合测试(一)
满分120分,限时100分钟
一、选择题(每小题3分,共36分)
1.(2023山东威海中考)我国民间建筑装饰图案中,蕴含着数学之美.下列图案中既是轴对称图形又是中心对称图形的是( )
A B C D
2.在-1.414,,-π,0,3.14,(-)0,,2+,3.212 212 221…(相邻两个1之间依次多1个2)中,无理数的个数为( )
A.5 B.2 C.3 D.4
3.(2022山东滨州中考)把不等式组中每个不等式的解集在同一条数轴上表示出来,正确的为( )
A B C D
4.【易错题】(2022山东聊城高唐期中)-64的立方根与的平方根之和是( )
A.-7 B.5 C.-13或5 D.-1或-7
5.(2023山东菏泽定陶期中)如图,已知平行四边形ABCD,下列结论中错误的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当AC=BD时,它是矩形
D.当∠ABC=90°时,它是正方形
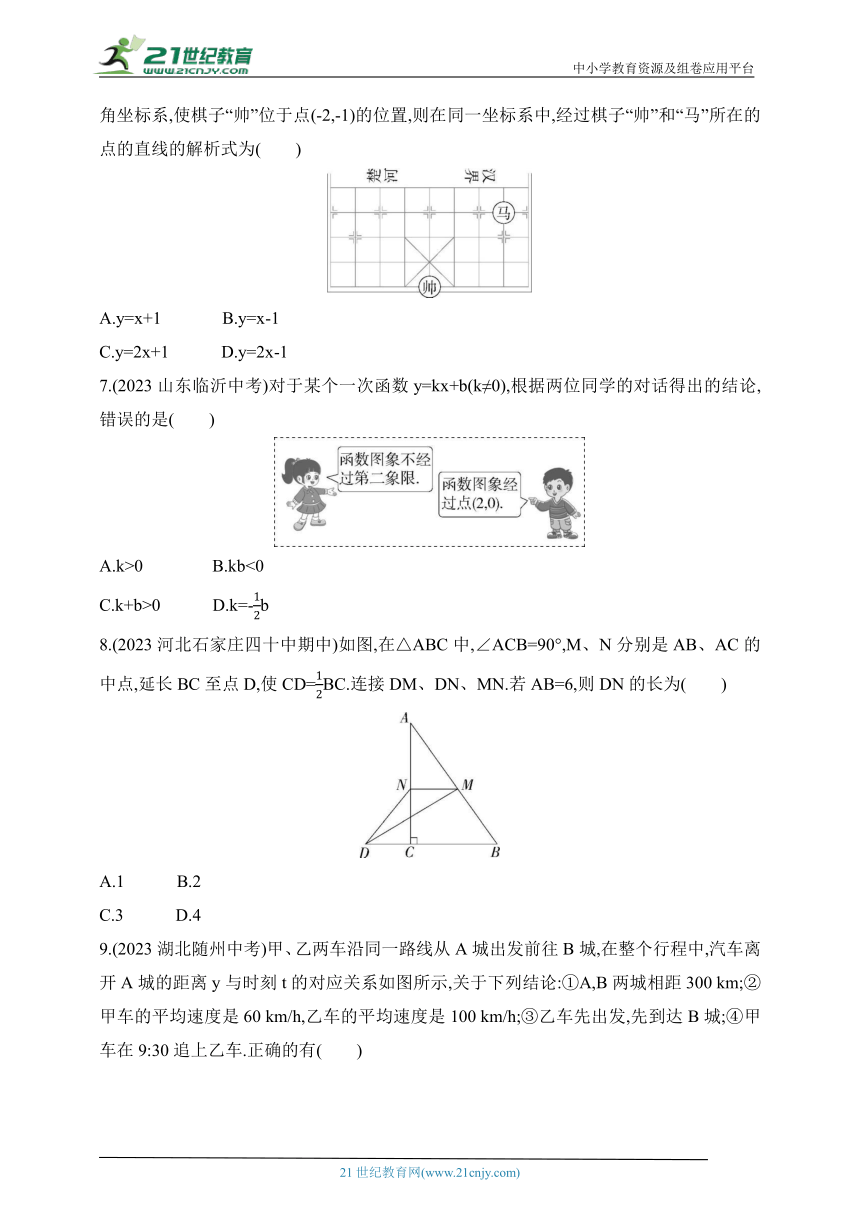
6.【中华优秀传统文化】(2023湖北鄂州中考改编)象棋起源于中国,中国象棋文化历史悠久.如图所示的是某次对弈的残图(其中每个小正方形的边长为1个单位),如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,则在同一坐标系中,经过棋子“帅”和“马”所在的点的直线的解析式为( )
A.y=x+1 B.y=x-1
C.y=2x+1 D.y=2x-1
7.(2023山东临沂中考)对于某个一次函数y=kx+b(k≠0),根据两位同学的对话得出的结论,错误的是( )
A.k>0 B.kb<0
C.k+b>0 D.k=-b
8.(2023河北石家庄四十中期中)如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=BC.连接DM、DN、MN.若AB=6,则DN的长为( )
A.1 B.2
C.3 D.4
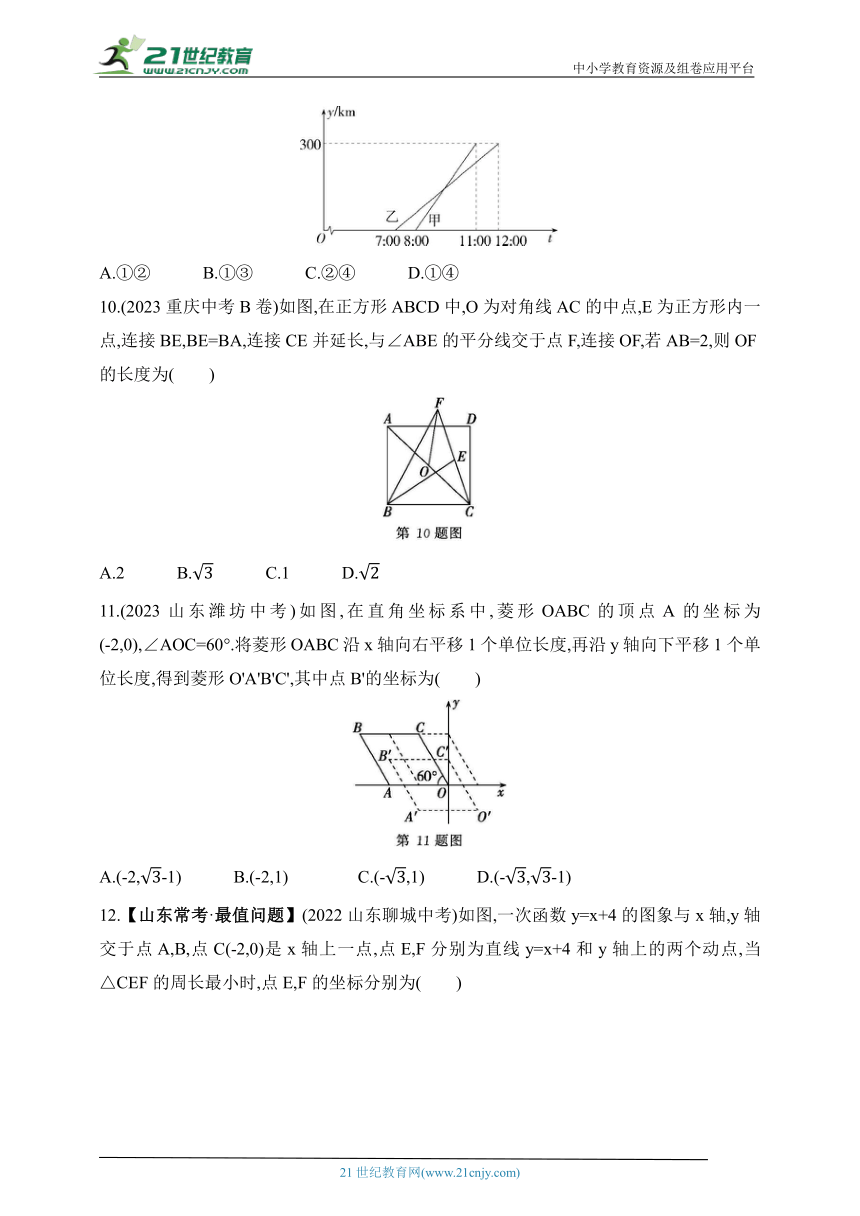
9.(2023湖北随州中考)甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,关于下列结论:①A,B两城相距300 km;②甲车的平均速度是60 km/h,乙车的平均速度是100 km/h;③乙车先出发,先到达B城;④甲车在9:30追上乙车.正确的有( )
A.①② B.①③ C.②④ D.①④
10.(2023重庆中考B卷)如图,在正方形ABCD中,O为对角线AC的中点,E为正方形内一点,连接BE,BE=BA,连接CE并延长,与∠ABE的平分线交于点F,连接OF,若AB=2,则OF的长度为( )
A.2 B. C.1 D.
11.(2023山东潍坊中考)如图,在直角坐标系中,菱形OABC的顶点A的坐标为(-2,0),∠AOC=60°.将菱形OABC沿x轴向右平移1个单位长度,再沿y轴向下平移1个单位长度,得到菱形O'A'B'C',其中点B'的坐标为( )
A.(-2,-1) B.(-2,1) C.(-,1) D.(-,-1)
12.【山东常考·最值问题】(2022山东聊城中考)如图,一次函数y=x+4的图象与x轴,y轴交于点A,B,点C(-2,0)是x轴上一点,点E,F分别为直线y=x+4和y轴上的两个动点,当△CEF的周长最小时,点E,F的坐标分别为( )
A.,(0,2) B.(-2,2),(0,2)
C., D.(-2,2),
二、填空题(每小题3分,共15分)
13.(2023山东聊城冠县期末)若点P(a+b,5)与点Q(-1,3a-b)关于原点对称,则ab= .
14.(2021四川眉山中考)若关于x的不等式x+m<1只有3个正整数解,则m的取值范围是 .
15.【新独家原创】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则EF的长为 .
16.(2023山东潍坊昌乐期末)如图,在矩形ABCD中,E在AD边上,将△ABE沿BE折叠,点A恰好落在矩形ABCD的对称中心O处,若AB=1,则BC的长为 .
17.如图所示的是某地区一种产品30天的销售情况的图象,图①是产品销售量y(单位:件)与时间t(单位:天)的函数关系图象,图②是每件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系图象,则第27天的日销售利润是 元.
三、解答题(共69分)
18.[含评分细则](2023山东聊城莘县期末)(8分)计算:
(1)(-)0++-.
(2)(3-1)(3+1)-(3-1)2.
19.[含评分细则](8分)已知关于x、y的方程组的解满足x为非正数,y为负数.
(1)求m的取值范围.
(2)化简:|m-3|-|m+2|.
(3)在m的取值范围内,当m为何整数时,关于x的不等式2mx+x<2m+1的解集为x>1
20.[含评分细则](2023山东济南济阳期中)(9分)如图,在正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点均在格点上,请在所给平面直角坐标系中按要求画图和解答问题.
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得到△AB1C1,画出△AB1C1,并写出点B1的坐标.
(2)作出与△ABC关于坐标原点O成中心对称的△A2B2C2,并写出点B2的坐标.
(3)作出点C关于x轴的对称点P.若点P向右平移m个单位长度后落在△A2B2C2的内部(不包含边上),请直接写出m的整数值.
21.[含评分细则]【“手拉手”全等模型】(10分)两个大小不等的、含45°角的三角尺(△ACB和△DCE)按如图①所示的方式放置,E,C,A三点在一条直线上,连接AD和BE.
(1)试判断线段BE和AD的关系,并说明理由.
(2)当△DCE绕点C顺时针旋转一定角度到如图②所示的位置时,请判断(1)的结论是否仍然成立,并说明理由.
图① 图②
22.[含评分细则](10分)为了感受大自然,描绘大自然的美景,小明和同学打算购买画笔与画板.已知购买2盒画笔和4个画板共需94元,购买4盒画笔和2个画板共需98元.
(1)购买一盒画笔和一个画板各需要多少元
(2)小明和同学商量,需要画笔盒数和画板个数总共为10,且购买这些写生工具的总费用不超过157元,则最少购买画板多少个
(3)在(2)的条件下,若最多购买画板8个,哪种购买方案更省钱
23.[含评分细则](2022四川德阳中考)(12分)如图,在菱形ABCD中,∠ABC=60°,AB=2,过点D作BC的垂线,交BC的延长线于点H.点F从点B出发沿BD方向以每秒2个单位长度的速度向点D匀速运动,同时,点E从点H出发沿HD方向以每秒1个单位长度的速度向点D匀速运动.设点E,F的运动时间为t(单位:s),且0(1)求证:四边形EFGH是矩形.
(2)连接FC,EC,点F,E在运动的过程中,△BFC与△DEC能否全等 若能,求出此时t的值;若不能,请说明理由.
24.[含评分细则](12分)如图,一次函数y1=2x-2的图象与y轴交于点A,一次函数y2的图象与y轴交于点B(0,6),点C为两函数图象的交点,且点C的横坐标为2.
(1)求一次函数y2的解析式.
(2)求△ABC的面积.
(3)问:在坐标轴上,是否存在一点P,使得S△ACP=2S△ABC 若存在,请写出点P的坐标;若不存在,请说明理由.
答案全解全析
一、选择题
1.A
2.D ,-π,2+,3.212 212 221…(相邻两个1之间依次多1个2)是无理数,故选D.
3.C 解不等式x-3<2x,得x>-3,解不等式≥,得x≤5,将两个不等式的解集在同一条数轴上表示如图所示.故选C.
4.D -64的立方根是-4,=9,9的平方根为±3,-4+3=-1,-4+(-3)=-7,故选D.
5.D 根据“有一组邻边相等的平行四边形叫做菱形”可知,选项A中结论正确;根据“对角线互相垂直的平行四边形是菱形”可知,选项B中结论正确;根据“对角线相等的平行四边形是矩形”可知,选项C中结论正确;根据“有一个角是直角的平行四边形叫做矩形”可知,选项D中结论错误.故选D.
6.A 由“帅”位于点(-2,-1)的位置,可得“马”位于点(1,2)的位置.设经过棋子“帅”和“马”所在的点的直线的解析式为y=kx+b,∴解得∴直线的解析式为y=x+1.
7.C ∵一次函数y=kx+b(k≠0)的图象经过点(2,0),不经过第二象限,∴图象经过第一、三、四象限,2k+b=0,∴k>0,b<0,k=-b,∴kb<0,k+b=b<0.故选C.
8.C 连接CM(图略),∵M、N分别是AB、AC的中点,
∴MN是△ABC的中位线,∴MN=BC,MN∥BC.
∵CD=BC,∴CD=MN,∴四边形NDCM为平行四边形,∴DN=CM.
∵∠ACB=90°,M是AB的中点,∴CM=AB=×6=3,∴DN=3,故选C.
9.D 由题图可知,A,B两城相距300 km,乙车先出发,甲车先到达B城,①正确,③错误;甲车的平均速度是300÷(11-8)=100(km/h),乙车的平均速度是300÷(12-7)=60(km/h),②错误;设甲车出发后x小时,追上乙车,100x=60(x+1),解得x=1.5,∴甲车出发1.5 h追上乙车.∵甲车8:00出发,∴甲车在9:30追上乙车,④正确.综上所述,正确的有①④.
10.D 如图,连接AF,∵四边形ABCD是正方形,BE=BA=2,
∴AB=BC=BE=2,∠ABC=90°,∴AC===2,∠BEC=∠BCE,
∵BF平分∠ABE,∴∠ABF=∠EBF,
在△BAF与△BEF中,∴△BAF≌△BEF(SAS),
∴∠BAF=∠BEF,∵∠BEC+∠BEF=180°,∠BEC=∠BCE,∴∠BCE+∠BAF=180°,
∴∠ABC+∠AFC=180°,∴∠AFC=90°,
∵O为对角线AC的中点,∴OF=AC=,故选D.
11.A 如图,过点B作BE⊥x轴于点E,∴∠BEA=90°.
∵点A的坐标为(-2,0),∴OA=2,∵四边形OABC是菱形,∴AB=OA=2,AB∥OC,
∴∠EAB=∠AOC=60°,∴∠ABE=30°,∴AE=AB=×2=1,
由勾股定理,得BE===,∴OE=AE+OA=1+2=3,
∴点B的坐标是(-3,).∵将菱形OABC沿x轴向右平移1个单位长度,再沿y轴向下平移1个单位长度,得到菱形O'A'B'C',∴点B'的坐标为(-3+1,-1),即(-2,-1),故选A.
12.C 如图,作点C(-2,0)关于y轴的对称点G(2,0),作点C(-2,0)关于直线y=x+4的对称点D,连接AD,连接DG交AB于E,交y轴于F,则DE=CE,CF=GF,所以CE+CF+EF=DE+GF+EF=DG,此时△CEF的周长最小.对于y=x+4,当y=0时,x=-4,当x=0时,y=4,所以A(-4,0),B(0,4),所以OA=OB=4,所以△AOB是等腰直角三角形,所以∠BAC=45°,因为C,D关于直线AB对称,
所以∠DAB=∠BAC=45°,AD=AC,所以∠DAC=∠DAB+∠BAC=90°.因为C(-2,0),所以OC=2,
所以AD=AC=OA-OC=2,所以D(-4,2).由D(-4,2),G(2,0)可得直线DG的解析式为y=-x+,
对于y=-x+,当x=0时,y=,所以F.
解方程组得
所以E,故选C.
二、填空题
13.答案 1
解析 由点P(a+b,5)与点Q(-1,3a-b)关于原点对称,得
解得∴ab=(-1)2=1.
14.答案 -3≤m<-2
解析 解不等式x+m<1,得x<1-m,
因为不等式x+m<1只有3个正整数解,
所以这3个正整数解为1,2,3,
所以3<1-m≤4,解得-3≤m<-2.
15.答案 3
解析 由题意可知,中间小正方形的边长为a-b,每个直角三角形的面积为ab=×8=4.
因为大正方形的面积是4个直角三角形的面积与中间小正方形的面积之和,
所以4×4+(a-b)2=25,所以(a-b)2=25-16=9.
由勾股定理,得EF====3.
16.答案
解析 如图,连接OD,∵将△ABE沿BE折叠得到△OBE,∴OB=BA=1.
∵四边形ABCD是矩形,O是它的对称中心,∴BD=2OB=2×1=2,BC=AD,∠BAD=90°,
∴AD===,∴BC=AD=.
17.答案 875
解析 由题图①可知,当24≤t≤30时,设y与t的函数解析式为y=kt+b(k≠0),
由题意得解得
∴当24≤t≤30时,y与t的函数解析式为y=-t+400,当t=27时,y=-×27+400=175,
故第27天的产品销售量为175件,
由题图②可知,当20≤t≤30时,每件产品的销售利润为5元,∴第27天的日销售利润为175×5=875(元).
三、解答题
18.解析 (1)原式=1-2+-2-………………2分
=-3.………………4分
(2)原式=(3)2-12-(18-6+1)………………6分
=18-1-18+6-1………………7分
=6-2.………………8分
19.解析 (1)解方程组,得………………1分
由题意知x≤0,y<0,∴解得-2(2)∵-20,∴|m-3|-|m+2|=3-m-m-2=1-2m.………………5分
(3)由2mx+x<2m+1得(2m+1)x<2m+1,
∵不等式的解集为x>1,∴2m+1<0,∴m<-,
∴-220.解析 (1)如图,△AB1C1即为所求.………………2分
点B1的坐标为(-3,1).………………3分
(2)如图,△A2B2C2即为所求.………………5分
点B2的坐标为(2,2).………………6分
(3)如图,点P即为所求.………………7分
由图可知,点P向右平移6个或7个单位长度后落在△A2B2C2的内部(不包含边上),
∴m的整数值为6或7.………………9分
21.解析 (1)BE=AD,BE⊥AD.………………1分
理由如下:
如图①,延长EB交AD于点F,………………2分
由题意知AC=BC,∠ACD=∠BCE=90°,CE=CD,
所以△ACD≌△BCE(SAS),………………3分
所以∠ADC=∠BEC,BE=AD.因为∠ADC+∠DAC=90°,所以∠BEC+∠DAC=90°,
所以∠AFE=90°,所以BE⊥AD.………………5分
(2)仍然成立.………………6分
理由如下:
如图②,延长EB交AD于点F,………………7分
因为∠ACB=∠DCE=90°,所以∠ACB-∠BCD=∠DCE-∠BCD,
即∠ACD=∠BCE,
又因为AC=BC,DC=EC,
所以△ACD≌△BCE(SAS).………………8分
所以AD=BE,∠ADC=∠BEC.
因为∠BEC+∠DEB+∠EDC=90°,
所以∠ADC +∠DEB+∠EDC=90°,
所以∠DFE=90°,所以BE⊥AD.………………10分
22.解析 (1)设购买一盒画笔需要x元,购买一个画板需要y元,
根据题意,得解得
答:购买一盒画笔需要17元,购买一个画板需要15元.………………3分
(2)设购买m个画板,则购买(10-m)盒画笔,
根据题意,得17(10-m)+15m≤157,解得m≥,
又∵m为正整数,∴m的最小值为7.
答:最少购买画板7个.………………6分
(3)∵最多购买画板8个,且m为正整数,
∴购买画板的个数可以为7或8,∴共有2种购买方案.
方案①,购买7个画板,3盒画笔,所需费用为15×7+17×3=156(元);
方案②,购买8个画板,2盒画笔,所需费用为15×8+17×2=154(元).
∵156>154,
∴购买8个画板,2盒画笔更省钱.………………10分
23.解析 (1)证明:因为EH⊥BC,FG⊥BH,所以EH∥FG.
由题意知BF=2t,EH=t,
因为四边形ABCD是菱形,∠ABC=60°,所以∠CBD=30°,
所以FG=BF=t,所以EH=FG,
所以四边形EFGH是平行四边形,
因为∠FGH=90°,所以四边形EFGH是矩形.………………5分
(2)△BFC与△DCE能全等,
因为四边形ABCD是菱形,∠ABC=60°,AB=2,
所以∠ADC=∠ABC=60°,CD=BC=AB=2,AB∥CD,∠ABD=∠CBD,∠ADB=∠CDB,
所以∠CBD=∠CDB=30°,∠DCH=∠ABC=60°,
因为DH⊥BC,所以∠CHD=90°,所以∠CDH=90°-60°=30°,
所以∠CDH=∠CBF,CH=CD=,
所以DH==3.因为BF=2t,EH=t,所以DE=3-t,
易知当BF=DE时,△BFC≌△DEC,
所以2t=3-t,解得t=1.………………12分
24.解析 (1)当x=2时,y1=2x-2=2,∴C(2,2),
设y2=kx+b(k≠0),
把B(0,6),C(2,2)代入可得解得
∴一次函数y2的解析式为y2=-2x+6.………………3分
(2)∵一次函数y1=2x-2的图象与y轴交于点A,
∴A(0,-2),∴S△ABC=×(6+2)×2=8.………………5分
(3)存在.∵S△ACP=2S△ABC,S△ABC=8,∴S△ACP=16.
当P在y轴上时,AP·xC=16,即AP×2=16,∴AP=16,
∵A(0,-2),∴点P的坐标为(0,14)或(0,-18).………………8分
当P在x轴上时,设直线y1=2x-2与x轴交于点D,∴D(1,0),
∴S△ACP=S△PCD+S△ADP=PD·|yC|+PD·|yA|=16,
∴PD×(2+2)=16,∴PD=8,
∵D(1,0),∴点P的坐标为(-7,0)或(9,0).………………11分
综上,在坐标轴上,存在一点P,使得S△ACP=2S△ABC,点P的坐标为(0,14)或(0,-18)或(-7,0)或(9,0).………………12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学八年级下学期
期末素养综合测试(一)
满分120分,限时100分钟
一、选择题(每小题3分,共36分)
1.(2023山东威海中考)我国民间建筑装饰图案中,蕴含着数学之美.下列图案中既是轴对称图形又是中心对称图形的是( )
A B C D
2.在-1.414,,-π,0,3.14,(-)0,,2+,3.212 212 221…(相邻两个1之间依次多1个2)中,无理数的个数为( )
A.5 B.2 C.3 D.4
3.(2022山东滨州中考)把不等式组中每个不等式的解集在同一条数轴上表示出来,正确的为( )
A B C D
4.【易错题】(2022山东聊城高唐期中)-64的立方根与的平方根之和是( )
A.-7 B.5 C.-13或5 D.-1或-7
5.(2023山东菏泽定陶期中)如图,已知平行四边形ABCD,下列结论中错误的是( )
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当AC=BD时,它是矩形
D.当∠ABC=90°时,它是正方形
6.【中华优秀传统文化】(2023湖北鄂州中考改编)象棋起源于中国,中国象棋文化历史悠久.如图所示的是某次对弈的残图(其中每个小正方形的边长为1个单位),如果建立平面直角坐标系,使棋子“帅”位于点(-2,-1)的位置,则在同一坐标系中,经过棋子“帅”和“马”所在的点的直线的解析式为( )
A.y=x+1 B.y=x-1
C.y=2x+1 D.y=2x-1
7.(2023山东临沂中考)对于某个一次函数y=kx+b(k≠0),根据两位同学的对话得出的结论,错误的是( )
A.k>0 B.kb<0
C.k+b>0 D.k=-b
8.(2023河北石家庄四十中期中)如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=BC.连接DM、DN、MN.若AB=6,则DN的长为( )
A.1 B.2
C.3 D.4
9.(2023湖北随州中考)甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,关于下列结论:①A,B两城相距300 km;②甲车的平均速度是60 km/h,乙车的平均速度是100 km/h;③乙车先出发,先到达B城;④甲车在9:30追上乙车.正确的有( )
A.①② B.①③ C.②④ D.①④
10.(2023重庆中考B卷)如图,在正方形ABCD中,O为对角线AC的中点,E为正方形内一点,连接BE,BE=BA,连接CE并延长,与∠ABE的平分线交于点F,连接OF,若AB=2,则OF的长度为( )
A.2 B. C.1 D.
11.(2023山东潍坊中考)如图,在直角坐标系中,菱形OABC的顶点A的坐标为(-2,0),∠AOC=60°.将菱形OABC沿x轴向右平移1个单位长度,再沿y轴向下平移1个单位长度,得到菱形O'A'B'C',其中点B'的坐标为( )
A.(-2,-1) B.(-2,1) C.(-,1) D.(-,-1)
12.【山东常考·最值问题】(2022山东聊城中考)如图,一次函数y=x+4的图象与x轴,y轴交于点A,B,点C(-2,0)是x轴上一点,点E,F分别为直线y=x+4和y轴上的两个动点,当△CEF的周长最小时,点E,F的坐标分别为( )
A.,(0,2) B.(-2,2),(0,2)
C., D.(-2,2),
二、填空题(每小题3分,共15分)
13.(2023山东聊城冠县期末)若点P(a+b,5)与点Q(-1,3a-b)关于原点对称,则ab= .
14.(2021四川眉山中考)若关于x的不等式x+m<1只有3个正整数解,则m的取值范围是 .
15.【新独家原创】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则EF的长为 .
16.(2023山东潍坊昌乐期末)如图,在矩形ABCD中,E在AD边上,将△ABE沿BE折叠,点A恰好落在矩形ABCD的对称中心O处,若AB=1,则BC的长为 .
17.如图所示的是某地区一种产品30天的销售情况的图象,图①是产品销售量y(单位:件)与时间t(单位:天)的函数关系图象,图②是每件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系图象,则第27天的日销售利润是 元.
三、解答题(共69分)
18.[含评分细则](2023山东聊城莘县期末)(8分)计算:
(1)(-)0++-.
(2)(3-1)(3+1)-(3-1)2.
19.[含评分细则](8分)已知关于x、y的方程组的解满足x为非正数,y为负数.
(1)求m的取值范围.
(2)化简:|m-3|-|m+2|.
(3)在m的取值范围内,当m为何整数时,关于x的不等式2mx+x<2m+1的解集为x>1
20.[含评分细则](2023山东济南济阳期中)(9分)如图,在正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点均在格点上,请在所给平面直角坐标系中按要求画图和解答问题.
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得到△AB1C1,画出△AB1C1,并写出点B1的坐标.
(2)作出与△ABC关于坐标原点O成中心对称的△A2B2C2,并写出点B2的坐标.
(3)作出点C关于x轴的对称点P.若点P向右平移m个单位长度后落在△A2B2C2的内部(不包含边上),请直接写出m的整数值.
21.[含评分细则]【“手拉手”全等模型】(10分)两个大小不等的、含45°角的三角尺(△ACB和△DCE)按如图①所示的方式放置,E,C,A三点在一条直线上,连接AD和BE.
(1)试判断线段BE和AD的关系,并说明理由.
(2)当△DCE绕点C顺时针旋转一定角度到如图②所示的位置时,请判断(1)的结论是否仍然成立,并说明理由.
图① 图②
22.[含评分细则](10分)为了感受大自然,描绘大自然的美景,小明和同学打算购买画笔与画板.已知购买2盒画笔和4个画板共需94元,购买4盒画笔和2个画板共需98元.
(1)购买一盒画笔和一个画板各需要多少元
(2)小明和同学商量,需要画笔盒数和画板个数总共为10,且购买这些写生工具的总费用不超过157元,则最少购买画板多少个
(3)在(2)的条件下,若最多购买画板8个,哪种购买方案更省钱
23.[含评分细则](2022四川德阳中考)(12分)如图,在菱形ABCD中,∠ABC=60°,AB=2,过点D作BC的垂线,交BC的延长线于点H.点F从点B出发沿BD方向以每秒2个单位长度的速度向点D匀速运动,同时,点E从点H出发沿HD方向以每秒1个单位长度的速度向点D匀速运动.设点E,F的运动时间为t(单位:s),且0
(2)连接FC,EC,点F,E在运动的过程中,△BFC与△DEC能否全等 若能,求出此时t的值;若不能,请说明理由.
24.[含评分细则](12分)如图,一次函数y1=2x-2的图象与y轴交于点A,一次函数y2的图象与y轴交于点B(0,6),点C为两函数图象的交点,且点C的横坐标为2.
(1)求一次函数y2的解析式.
(2)求△ABC的面积.
(3)问:在坐标轴上,是否存在一点P,使得S△ACP=2S△ABC 若存在,请写出点P的坐标;若不存在,请说明理由.
答案全解全析
一、选择题
1.A
2.D ,-π,2+,3.212 212 221…(相邻两个1之间依次多1个2)是无理数,故选D.
3.C 解不等式x-3<2x,得x>-3,解不等式≥,得x≤5,将两个不等式的解集在同一条数轴上表示如图所示.故选C.
4.D -64的立方根是-4,=9,9的平方根为±3,-4+3=-1,-4+(-3)=-7,故选D.
5.D 根据“有一组邻边相等的平行四边形叫做菱形”可知,选项A中结论正确;根据“对角线互相垂直的平行四边形是菱形”可知,选项B中结论正确;根据“对角线相等的平行四边形是矩形”可知,选项C中结论正确;根据“有一个角是直角的平行四边形叫做矩形”可知,选项D中结论错误.故选D.
6.A 由“帅”位于点(-2,-1)的位置,可得“马”位于点(1,2)的位置.设经过棋子“帅”和“马”所在的点的直线的解析式为y=kx+b,∴解得∴直线的解析式为y=x+1.
7.C ∵一次函数y=kx+b(k≠0)的图象经过点(2,0),不经过第二象限,∴图象经过第一、三、四象限,2k+b=0,∴k>0,b<0,k=-b,∴kb<0,k+b=b<0.故选C.
8.C 连接CM(图略),∵M、N分别是AB、AC的中点,
∴MN是△ABC的中位线,∴MN=BC,MN∥BC.
∵CD=BC,∴CD=MN,∴四边形NDCM为平行四边形,∴DN=CM.
∵∠ACB=90°,M是AB的中点,∴CM=AB=×6=3,∴DN=3,故选C.
9.D 由题图可知,A,B两城相距300 km,乙车先出发,甲车先到达B城,①正确,③错误;甲车的平均速度是300÷(11-8)=100(km/h),乙车的平均速度是300÷(12-7)=60(km/h),②错误;设甲车出发后x小时,追上乙车,100x=60(x+1),解得x=1.5,∴甲车出发1.5 h追上乙车.∵甲车8:00出发,∴甲车在9:30追上乙车,④正确.综上所述,正确的有①④.
10.D 如图,连接AF,∵四边形ABCD是正方形,BE=BA=2,
∴AB=BC=BE=2,∠ABC=90°,∴AC===2,∠BEC=∠BCE,
∵BF平分∠ABE,∴∠ABF=∠EBF,
在△BAF与△BEF中,∴△BAF≌△BEF(SAS),
∴∠BAF=∠BEF,∵∠BEC+∠BEF=180°,∠BEC=∠BCE,∴∠BCE+∠BAF=180°,
∴∠ABC+∠AFC=180°,∴∠AFC=90°,
∵O为对角线AC的中点,∴OF=AC=,故选D.
11.A 如图,过点B作BE⊥x轴于点E,∴∠BEA=90°.
∵点A的坐标为(-2,0),∴OA=2,∵四边形OABC是菱形,∴AB=OA=2,AB∥OC,
∴∠EAB=∠AOC=60°,∴∠ABE=30°,∴AE=AB=×2=1,
由勾股定理,得BE===,∴OE=AE+OA=1+2=3,
∴点B的坐标是(-3,).∵将菱形OABC沿x轴向右平移1个单位长度,再沿y轴向下平移1个单位长度,得到菱形O'A'B'C',∴点B'的坐标为(-3+1,-1),即(-2,-1),故选A.
12.C 如图,作点C(-2,0)关于y轴的对称点G(2,0),作点C(-2,0)关于直线y=x+4的对称点D,连接AD,连接DG交AB于E,交y轴于F,则DE=CE,CF=GF,所以CE+CF+EF=DE+GF+EF=DG,此时△CEF的周长最小.对于y=x+4,当y=0时,x=-4,当x=0时,y=4,所以A(-4,0),B(0,4),所以OA=OB=4,所以△AOB是等腰直角三角形,所以∠BAC=45°,因为C,D关于直线AB对称,
所以∠DAB=∠BAC=45°,AD=AC,所以∠DAC=∠DAB+∠BAC=90°.因为C(-2,0),所以OC=2,
所以AD=AC=OA-OC=2,所以D(-4,2).由D(-4,2),G(2,0)可得直线DG的解析式为y=-x+,
对于y=-x+,当x=0时,y=,所以F.
解方程组得
所以E,故选C.
二、填空题
13.答案 1
解析 由点P(a+b,5)与点Q(-1,3a-b)关于原点对称,得
解得∴ab=(-1)2=1.
14.答案 -3≤m<-2
解析 解不等式x+m<1,得x<1-m,
因为不等式x+m<1只有3个正整数解,
所以这3个正整数解为1,2,3,
所以3<1-m≤4,解得-3≤m<-2.
15.答案 3
解析 由题意可知,中间小正方形的边长为a-b,每个直角三角形的面积为ab=×8=4.
因为大正方形的面积是4个直角三角形的面积与中间小正方形的面积之和,
所以4×4+(a-b)2=25,所以(a-b)2=25-16=9.
由勾股定理,得EF====3.
16.答案
解析 如图,连接OD,∵将△ABE沿BE折叠得到△OBE,∴OB=BA=1.
∵四边形ABCD是矩形,O是它的对称中心,∴BD=2OB=2×1=2,BC=AD,∠BAD=90°,
∴AD===,∴BC=AD=.
17.答案 875
解析 由题图①可知,当24≤t≤30时,设y与t的函数解析式为y=kt+b(k≠0),
由题意得解得
∴当24≤t≤30时,y与t的函数解析式为y=-t+400,当t=27时,y=-×27+400=175,
故第27天的产品销售量为175件,
由题图②可知,当20≤t≤30时,每件产品的销售利润为5元,∴第27天的日销售利润为175×5=875(元).
三、解答题
18.解析 (1)原式=1-2+-2-………………2分
=-3.………………4分
(2)原式=(3)2-12-(18-6+1)………………6分
=18-1-18+6-1………………7分
=6-2.………………8分
19.解析 (1)解方程组,得………………1分
由题意知x≤0,y<0,∴解得-2
(3)由2mx+x<2m+1得(2m+1)x<2m+1,
∵不等式的解集为x>1,∴2m+1<0,∴m<-,
∴-2
点B1的坐标为(-3,1).………………3分
(2)如图,△A2B2C2即为所求.………………5分
点B2的坐标为(2,2).………………6分
(3)如图,点P即为所求.………………7分
由图可知,点P向右平移6个或7个单位长度后落在△A2B2C2的内部(不包含边上),
∴m的整数值为6或7.………………9分
21.解析 (1)BE=AD,BE⊥AD.………………1分
理由如下:
如图①,延长EB交AD于点F,………………2分
由题意知AC=BC,∠ACD=∠BCE=90°,CE=CD,
所以△ACD≌△BCE(SAS),………………3分
所以∠ADC=∠BEC,BE=AD.因为∠ADC+∠DAC=90°,所以∠BEC+∠DAC=90°,
所以∠AFE=90°,所以BE⊥AD.………………5分
(2)仍然成立.………………6分
理由如下:
如图②,延长EB交AD于点F,………………7分
因为∠ACB=∠DCE=90°,所以∠ACB-∠BCD=∠DCE-∠BCD,
即∠ACD=∠BCE,
又因为AC=BC,DC=EC,
所以△ACD≌△BCE(SAS).………………8分
所以AD=BE,∠ADC=∠BEC.
因为∠BEC+∠DEB+∠EDC=90°,
所以∠ADC +∠DEB+∠EDC=90°,
所以∠DFE=90°,所以BE⊥AD.………………10分
22.解析 (1)设购买一盒画笔需要x元,购买一个画板需要y元,
根据题意,得解得
答:购买一盒画笔需要17元,购买一个画板需要15元.………………3分
(2)设购买m个画板,则购买(10-m)盒画笔,
根据题意,得17(10-m)+15m≤157,解得m≥,
又∵m为正整数,∴m的最小值为7.
答:最少购买画板7个.………………6分
(3)∵最多购买画板8个,且m为正整数,
∴购买画板的个数可以为7或8,∴共有2种购买方案.
方案①,购买7个画板,3盒画笔,所需费用为15×7+17×3=156(元);
方案②,购买8个画板,2盒画笔,所需费用为15×8+17×2=154(元).
∵156>154,
∴购买8个画板,2盒画笔更省钱.………………10分
23.解析 (1)证明:因为EH⊥BC,FG⊥BH,所以EH∥FG.
由题意知BF=2t,EH=t,
因为四边形ABCD是菱形,∠ABC=60°,所以∠CBD=30°,
所以FG=BF=t,所以EH=FG,
所以四边形EFGH是平行四边形,
因为∠FGH=90°,所以四边形EFGH是矩形.………………5分
(2)△BFC与△DCE能全等,
因为四边形ABCD是菱形,∠ABC=60°,AB=2,
所以∠ADC=∠ABC=60°,CD=BC=AB=2,AB∥CD,∠ABD=∠CBD,∠ADB=∠CDB,
所以∠CBD=∠CDB=30°,∠DCH=∠ABC=60°,
因为DH⊥BC,所以∠CHD=90°,所以∠CDH=90°-60°=30°,
所以∠CDH=∠CBF,CH=CD=,
所以DH==3.因为BF=2t,EH=t,所以DE=3-t,
易知当BF=DE时,△BFC≌△DEC,
所以2t=3-t,解得t=1.………………12分
24.解析 (1)当x=2时,y1=2x-2=2,∴C(2,2),
设y2=kx+b(k≠0),
把B(0,6),C(2,2)代入可得解得
∴一次函数y2的解析式为y2=-2x+6.………………3分
(2)∵一次函数y1=2x-2的图象与y轴交于点A,
∴A(0,-2),∴S△ABC=×(6+2)×2=8.………………5分
(3)存在.∵S△ACP=2S△ABC,S△ABC=8,∴S△ACP=16.
当P在y轴上时,AP·xC=16,即AP×2=16,∴AP=16,
∵A(0,-2),∴点P的坐标为(0,14)或(0,-18).………………8分
当P在x轴上时,设直线y1=2x-2与x轴交于点D,∴D(1,0),
∴S△ACP=S△PCD+S△ADP=PD·|yC|+PD·|yA|=16,
∴PD×(2+2)=16,∴PD=8,
∵D(1,0),∴点P的坐标为(-7,0)或(9,0).………………11分
综上,在坐标轴上,存在一点P,使得S△ACP=2S△ABC,点P的坐标为(0,14)或(0,-18)或(-7,0)或(9,0).………………12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
