2024青岛版数学八年级下学期--专项素养综合全练(八)一次函数的实际应用(含解析)
文档属性
| 名称 | 2024青岛版数学八年级下学期--专项素养综合全练(八)一次函数的实际应用(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 320.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024青岛版数学八年级下学期
专项素养综合全练(八)
一次函数的实际应用
类型一 利用一次函数解决分段函数问题
1.(2023吉林中考改编)甲、乙两个工程组同时挖掘沈白高铁某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务.甲、乙两组挖掘的长度之和y(m)与甲组挖掘时间x(天)之间的关系如图所示.
(1)甲组比乙组多挖掘了 天.
(2)求乙组停工后y关于x的函数解析式.
(3)当甲组挖掘的总长度与乙组挖掘的总长度相等时,求出乙组已停工的天数.
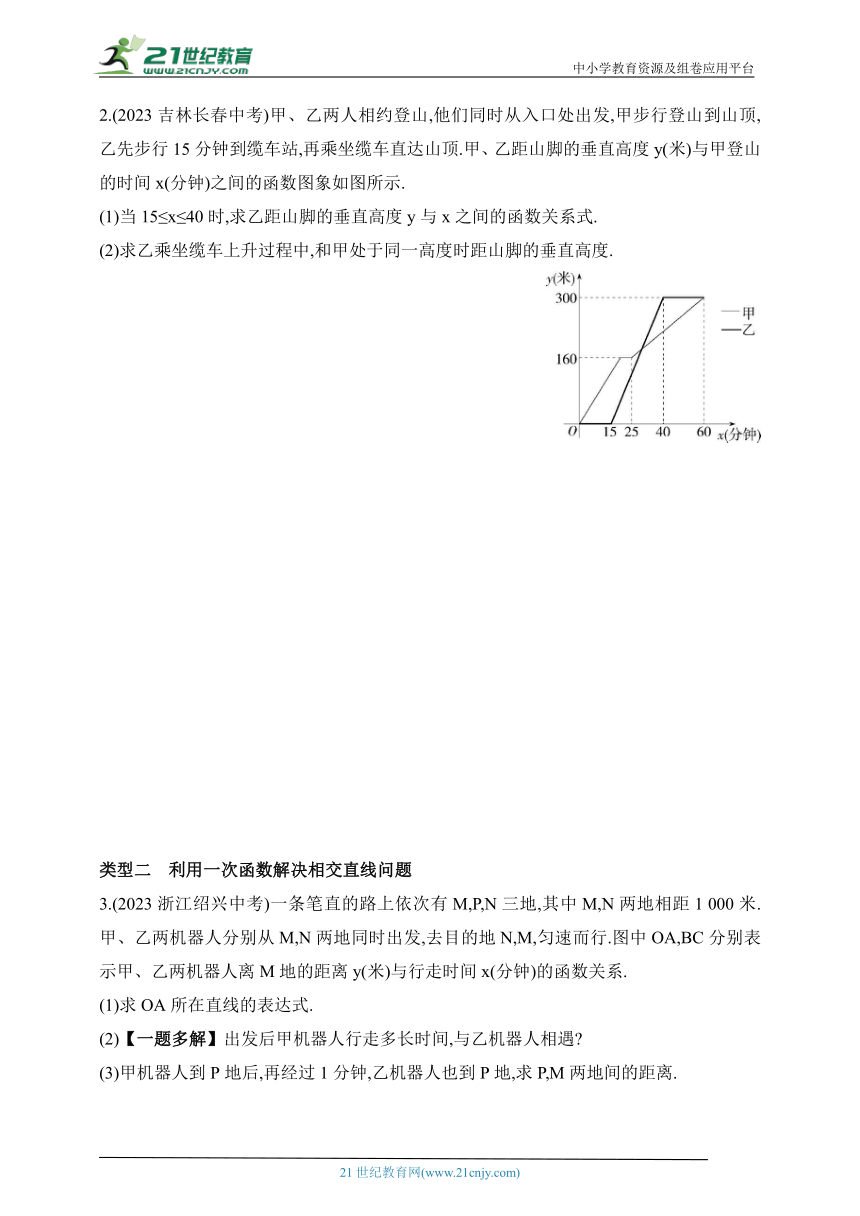
2.(2023吉林长春中考)甲、乙两人相约登山,他们同时从入口处出发,甲步行登山到山顶,乙先步行15分钟到缆车站,再乘坐缆车直达山顶.甲、乙距山脚的垂直高度y(米)与甲登山的时间x(分钟)之间的函数图象如图所示.
(1)当15≤x≤40时,求乙距山脚的垂直高度y与x之间的函数关系式.
(2)求乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度.
类型二 利用一次函数解决相交直线问题
3.(2023浙江绍兴中考)一条笔直的路上依次有M,P,N三地,其中M,N两地相距1 000米.甲、乙两机器人分别从M,N两地同时出发,去目的地N,M,匀速而行.图中OA,BC分别表示甲、乙两机器人离M地的距离y(米)与行走时间x(分钟)的函数关系.
(1)求OA所在直线的表达式.
(2)【一题多解】出发后甲机器人行走多长时间,与乙机器人相遇
(3)甲机器人到P地后,再经过1分钟,乙机器人也到P地,求P,M两地间的距离.
类型三 利用一次函数解决生活中的实际问题
4.(2023山东聊城莘县期末)为了提高同学们学习数学的兴趣,聊城市某中学开展主题为“感受数学魅力,享受数学乐趣”的数学活动.该学校计划购买A、B两种奖品奖励在数学活动中表现突出的学生,已知购买1件A种奖品和2件B种奖品共需64元,购买2件A种奖品和1件B种奖品共需56元.
(1)A、B两种奖品每件的价格各是多少元
(2)根据需要,该学校准备购买A、B两种奖品共80件(两种奖品都购买),设购买a件A种奖品,所需总费用为w元,求w与a的函数关系式,并直接写出a的取值范围.
(3)在(2)的条件下,若要求购买的A种奖品的数量不超过B种奖品数量的3倍,求所需总费用的最小值.
答案全解全析
1.解析 (1)30.
解答提示:由图象可知,甲、乙两组合作共挖掘了30天,甲组单独挖掘了60-30=30(天),即甲组比乙组多挖掘了30天.
(2)设乙组停工后y关于x的函数解析式为y=kx+b(k≠0),把点(30,210),(60,300)代入,得解得
∴y关于x的函数解析式为y=3x+120.
(3)由图象可知,甲组单独挖掘了30天,挖掘的长度是300-210=90(m),
∴甲组每天挖3 m.前30天甲、乙两组合作共挖掘了210 m,则乙组单独挖掘的长度是210-90=120(m).当甲组挖掘的长度是120 m时,甲组挖掘的天数是120÷3=40,乙组已停工的天数是40-30=10.
2.解析 (1)设当15≤x≤40时,乙距山脚的垂直高度y与x之间的函数关系式为y=kx+b(k≠0),
由题意得解得
∴当15≤x≤40时,乙距山脚的垂直高度y与x之间的函数关系式为y=12x-180.
(2)设当25≤x≤60时,甲距山脚的垂直高度y与x之间的函数解析式为y=mx+n(m≠0),将(25,160)和(60,300)代入,得
解得∴y=4x+60.
解方程组得
∴乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度为180米.
3.解析 (1)设OA所在直线的表达式为y=kx(k≠0),
∵A(5,1 000),∴1 000=5k,解得k=200,
∴OA所在直线的表达式为y=200x.
(2)解法一:由题图可知,甲机器人的速度为1 000÷5=200(米/分),乙机器人的速度为1 000÷10=100(米/分),
两机器人相遇时,所用时间为=(分钟).
答:出发后,甲机器人行走分钟时,与乙机器人相遇.
解法二:设BC所在直线的表达式为y=mx+n(m≠0),
将B(0,1 000),C(10,0)代入上式,得
解得∴BC所在直线的表达式为y=-100x+1 000,
联立解得
答:出发后,甲机器人行走分钟时,与乙机器人相遇.
(3)设甲机器人行走t分钟到P地,则P地与M地的距离为200t米,乙机器人行走(t+1)分钟后到P地,
∴P地与M地的距离为[1 000-100(t+1)]米,
∴200t=1 000-100(t+1),解得t=3,∴200t=600.
答:P,M两地间的距离为600米.
4.解析 (1)设每件A种奖品的价格是x元,每件B种奖品的价格是y元,
根据题意,得解得
答:每件A种奖品的价格是16元,每件B种奖品的价格是24元.
(2)根据题意,得w=16a+24(80-a)=-8a+1 920,
∴w与a的函数关系式为w=-8a+1 920(0(3)∵购买的A种奖品的数量不超过B种奖品数量的3倍,
∴a≤3(80-a),解得a≤60,∴0在w=-8a+1 920中,-8<0,∴w随a的增大而减小,
∴当a=60时,w最小,最小值为-8×60+1 920=1 440.
答:所需总费用的最小值是1 440.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024青岛版数学八年级下学期
专项素养综合全练(八)
一次函数的实际应用
类型一 利用一次函数解决分段函数问题
1.(2023吉林中考改编)甲、乙两个工程组同时挖掘沈白高铁某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务.甲、乙两组挖掘的长度之和y(m)与甲组挖掘时间x(天)之间的关系如图所示.
(1)甲组比乙组多挖掘了 天.
(2)求乙组停工后y关于x的函数解析式.
(3)当甲组挖掘的总长度与乙组挖掘的总长度相等时,求出乙组已停工的天数.
2.(2023吉林长春中考)甲、乙两人相约登山,他们同时从入口处出发,甲步行登山到山顶,乙先步行15分钟到缆车站,再乘坐缆车直达山顶.甲、乙距山脚的垂直高度y(米)与甲登山的时间x(分钟)之间的函数图象如图所示.
(1)当15≤x≤40时,求乙距山脚的垂直高度y与x之间的函数关系式.
(2)求乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度.
类型二 利用一次函数解决相交直线问题
3.(2023浙江绍兴中考)一条笔直的路上依次有M,P,N三地,其中M,N两地相距1 000米.甲、乙两机器人分别从M,N两地同时出发,去目的地N,M,匀速而行.图中OA,BC分别表示甲、乙两机器人离M地的距离y(米)与行走时间x(分钟)的函数关系.
(1)求OA所在直线的表达式.
(2)【一题多解】出发后甲机器人行走多长时间,与乙机器人相遇
(3)甲机器人到P地后,再经过1分钟,乙机器人也到P地,求P,M两地间的距离.
类型三 利用一次函数解决生活中的实际问题
4.(2023山东聊城莘县期末)为了提高同学们学习数学的兴趣,聊城市某中学开展主题为“感受数学魅力,享受数学乐趣”的数学活动.该学校计划购买A、B两种奖品奖励在数学活动中表现突出的学生,已知购买1件A种奖品和2件B种奖品共需64元,购买2件A种奖品和1件B种奖品共需56元.
(1)A、B两种奖品每件的价格各是多少元
(2)根据需要,该学校准备购买A、B两种奖品共80件(两种奖品都购买),设购买a件A种奖品,所需总费用为w元,求w与a的函数关系式,并直接写出a的取值范围.
(3)在(2)的条件下,若要求购买的A种奖品的数量不超过B种奖品数量的3倍,求所需总费用的最小值.
答案全解全析
1.解析 (1)30.
解答提示:由图象可知,甲、乙两组合作共挖掘了30天,甲组单独挖掘了60-30=30(天),即甲组比乙组多挖掘了30天.
(2)设乙组停工后y关于x的函数解析式为y=kx+b(k≠0),把点(30,210),(60,300)代入,得解得
∴y关于x的函数解析式为y=3x+120.
(3)由图象可知,甲组单独挖掘了30天,挖掘的长度是300-210=90(m),
∴甲组每天挖3 m.前30天甲、乙两组合作共挖掘了210 m,则乙组单独挖掘的长度是210-90=120(m).当甲组挖掘的长度是120 m时,甲组挖掘的天数是120÷3=40,乙组已停工的天数是40-30=10.
2.解析 (1)设当15≤x≤40时,乙距山脚的垂直高度y与x之间的函数关系式为y=kx+b(k≠0),
由题意得解得
∴当15≤x≤40时,乙距山脚的垂直高度y与x之间的函数关系式为y=12x-180.
(2)设当25≤x≤60时,甲距山脚的垂直高度y与x之间的函数解析式为y=mx+n(m≠0),将(25,160)和(60,300)代入,得
解得∴y=4x+60.
解方程组得
∴乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度为180米.
3.解析 (1)设OA所在直线的表达式为y=kx(k≠0),
∵A(5,1 000),∴1 000=5k,解得k=200,
∴OA所在直线的表达式为y=200x.
(2)解法一:由题图可知,甲机器人的速度为1 000÷5=200(米/分),乙机器人的速度为1 000÷10=100(米/分),
两机器人相遇时,所用时间为=(分钟).
答:出发后,甲机器人行走分钟时,与乙机器人相遇.
解法二:设BC所在直线的表达式为y=mx+n(m≠0),
将B(0,1 000),C(10,0)代入上式,得
解得∴BC所在直线的表达式为y=-100x+1 000,
联立解得
答:出发后,甲机器人行走分钟时,与乙机器人相遇.
(3)设甲机器人行走t分钟到P地,则P地与M地的距离为200t米,乙机器人行走(t+1)分钟后到P地,
∴P地与M地的距离为[1 000-100(t+1)]米,
∴200t=1 000-100(t+1),解得t=3,∴200t=600.
答:P,M两地间的距离为600米.
4.解析 (1)设每件A种奖品的价格是x元,每件B种奖品的价格是y元,
根据题意,得解得
答:每件A种奖品的价格是16元,每件B种奖品的价格是24元.
(2)根据题意,得w=16a+24(80-a)=-8a+1 920,
∴w与a的函数关系式为w=-8a+1 920(0
∴a≤3(80-a),解得a≤60,∴0
∴当a=60时,w最小,最小值为-8×60+1 920=1 440.
答:所需总费用的最小值是1 440.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
