10.1 轴对称 课件(共79张PPT) 华东师大版数学七年级下册
文档属性
| 名称 | 10.1 轴对称 课件(共79张PPT) 华东师大版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 20:41:17 | ||
图片预览











文档简介
(共79张PPT)
10.1 轴对称
第1课时 生活中的轴对称
华东师大版数学七年级下册
第10章 轴对称、平移与旋转
新课导入
观察下列图片说说你有何发现?
这些美丽的图形来自生活,你能发现这些图形有什么共同特征吗?用自己的语言描述.
自远古以来,对称形式被认为是和谐、美丽的.不论在自然界里还是在建筑中,不论在艺术中还是在科学中,甚至最普通的日常生活用品中,对称的形式都随处可见.
生活中的轴对称
拱桥
埃菲尔铁塔
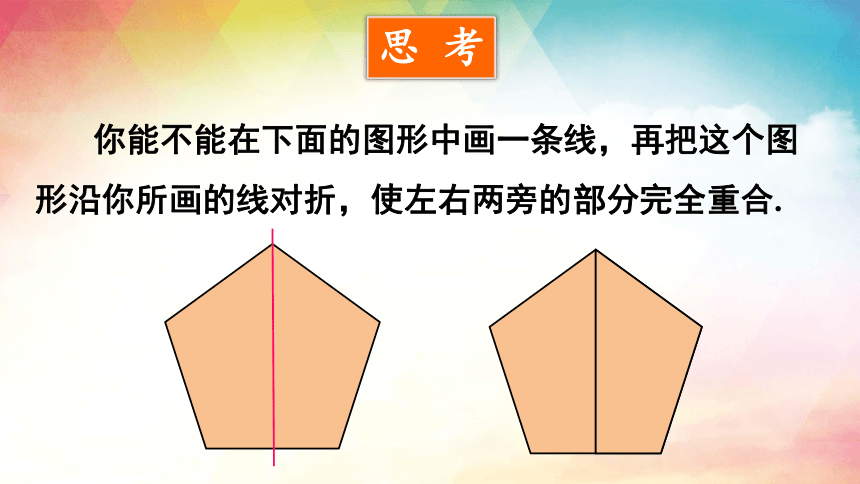
思 考
你能不能在下面的图形中画一条线,再把这个图形沿你所画的线对折,使左右两旁的部分完全重合.
如果一个图形沿某条直线对折后,直线两旁的部分能够_________,那么这个图形叫做轴对称图形.
轴对称图形的定义
完全重合
这条直线叫这个图形的对称轴.
练 习
找出图中各图形的对称轴. 是否有些图形的对称轴不止一条呢?
判断一个图形为轴对称图形方法:
(1)沿某条直线对折;
(2)直线两旁的部分能够完全重合.
轴对称
观察下面两组图形.
想一想 当把这两个天使沿着一条直线折叠后,会发现什么样的现象?
沿着一条直线折叠后,这两个五边形会有什么现象?
像这样,把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称.
这条直线就是对称轴.
两个图形的对应点(即两个图形重合时互相重合的点)叫做对称点.
你能举出生活中两个图形成轴对称的例子吗?
说一说
日常生活中,我们经常会照镜子,而镜子中的像与本人就关于镜面成轴对称.
做一做
请你标出图中A、B、C三点的对称点A1、B1、C1.
A
B
C
A1
B1
C1
轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的,所以它的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
轴对称图形的基本特征
剪纸艺术
随堂练习
1.下列图形中,一定是轴对称图形的是( )
A.锐角三角形 B.曲线
C.线段 D.直角三角形
C
2. 等腰三角形的对称轴有( )
A.一条 B.二条
C.三条 D.一条或三条
D
3.如图,哪一个选项中的右边图形与左边图形成轴对称( )
A
B
C
D
C
4.下列交通标志中哪些是轴对称图形?
×
√
×
√
10.1 轴对称
第2课时 轴对称的再认识
华东师大版数学七年级下册
第10章 轴对称、平移与旋转
新课导入
观察线段和角,它们都是轴对称图形吗?
A
B
O
C
D
把一个图形沿某条直线对折,对折后的两部分能完全重合,这样的图形称为轴对称图形.
什么是轴对称图形?
新课推进
在纸上画出线段AB及它的中点O,再过O点画与AB垂直的直线CD,沿直线CD将纸对折,观察线段OA和线段OB是否重合?
A
B
O
C
D
在上述试验中,显然线段OA和线段OB互相重合,因此,线段AB是轴对称图形.
A
B
O
C
D
垂直并且平分一条线段的直线称为这条线段的垂直平分线.
A
B
O
C
D
上图中直线CD是线段AB的垂直平分线. 线段的垂直平分线是一条直线.
垂直平分线又可称为中垂线.
线段的对称轴是什么?它是唯一的吗?
思 考
线段的对称轴有两条,一条是它的垂直平分线所在的直线,另一条是这条线段所在的直线.
A
B
在纸上画一个角∠AOB,然后对折这个角,使角的两条边完全重合,然后用直尺画出折痕OM. 看看射线OM与∠AOB是什么关系.
试一试
O
A
B
M
O
A
B
M
角是轴对称图形,对称轴是它的角平分线所在的直线.
有时我们感觉一个图形是轴对称的,那么如何来验证呢?这就需要我们去找到它的对称轴,看看沿着对称轴翻折以后两部分是否重合.
如图,方格纸内的两图形都是轴对称图形,请画出它们的对称轴.
试一试
在上图中,由于图形在方格纸内,我们可以凭直觉很准确地画出两个图形的对称轴,你能想想是什么原因吗?
因为在方格纸中我们比较容易看清楚图形的位置,也就比较容易确定图形的中间位置.
如果没有方格纸,而又不能折叠,你还能比较容易地画出图形的对称轴吗?请同学试试看,如下图的对称轴我们应该如何去画呢?
(1)
(2)
如图点 A 和点 A′ 关于某直线对称,你能画出这条直线吗?
做一做
A
A′
l
如图,连结点 A 和点 A′,画出线段 AA′ 的垂直平分线 l,则直线 l 就是所是点 A 和点 A′ 的对称轴.
A
A′
l
总 结
轴对称图形对称轴的画法:
1.找出轴对称图形的任意一组对称点,连结对称点.
2.画出连接对称点的线段的垂直平分线.则这条垂直平分线就是它的对称轴.
如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
随堂练习
1.下列说法错误的是( )
A.等边三角形是轴对称图形
B.轴对称图形的对应边相等,对应角相等
C.成轴对称的两条线段必在对称轴一侧
D.成轴对称的两个图形对应点的连线被对称轴垂直平分
C
2.下面的一些虚线,哪些是图形对称轴,哪些不是图形的对称轴?
②④⑥是图形的对称轴
3.已知,直线 a 与直线 b 是两条相交直线,它是轴对称图形吗?如果是,它有几条对称轴?画图试试看.
a
b
是轴对称图形,有2条对称轴.
4. 画出以下图形的对称轴.
10.1 轴对称
第3课时 画轴对称图形
华东师大版数学七年级下册
第10章 轴对称、平移与旋转
新课导入
上节课我们学习了画两个图形或一个图形的对称轴.请同学们为下面的两张轴对称图形画出对称轴.
将画好的轴对称图形遮掉左边一半或右边一半后,你能还原出原来的图形来吗?
想一想
如果给出一个图形和一条直线,那么如何画出这个图形关于这条直线的对称图形呢?
新课推进
如图,实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形.
试一试
A
B
C
A′
B′
C′
画完之后,请同学们思考下面两个问题:
(1)你可以通过什么方法来验证你画得是否正确.
(2)和其他同学比较一下,你的方法是最简单吗?
在格点图中,大家会很容易画出已知图形的轴对称图形,如果没有格点,你还能比较准确地画出已知图形的轴对称图形吗?
如图,已知点 A 和直线 l ,试画出点 A 关于直线 l 的对称点 A′.
做一做
(1)过点 A 向直线 l 画垂线段 AO,垂足点 O;
(2)延长AO至OA′,使OA′ = OA.则点 A′ 就是点 A关于直线 l 的对称点.
A
l
O
A′
你能画出线段 AB 关于直线 l 的对称线段吗?
练 习
l
(1)画点A、点B关于直线l的对称点A′ 、B′;
(2)连结A′、B′ .
则线段 A′B′ 就是线段AB关于直线 l 的对称线段.
A
B
A′
B′
例 已知△ABC,直线 l,画出△ABC关于直线 l 对称的图形.
l
A
B
C
A′
B′
C′
(1)分别画出点A、B 和 C 点关于直线 l 的对称点A′、B′ 和 C′;
(2)连结 A′B′、B′C′、A′C′、则△A′B′C′ 就是△ABC关于直线 l 的对称三角形.
步 骤
从上面的例子可以知道,如果图形是由直线、线段或射线组成时,那么只要画出图形中的特殊点的对称点,然后连接对称点,就可以画出关于这条直线的对称图形.
随堂练习
1.下列各图都是一个汉字的一半,你能想像出它的另一半并能确定它是什么字吗 (有几个字的笔划在对称轴上.)
品
口
来
晶
品
口
来
晶
2. 如图,作字母 M 关于 y 轴的轴对称图形并写出所得图形相应各端点的坐标.
x
y
A
B(-4,3)
C(-2.5,0)
D(-1,3)
E
E1
C1(2.5,0)
A1
B1(4,3)
D1(1,3)
3.如图,已知△ABC 和直线 MN. 求作△A′B′C′,使△A′B′C′ 和 △ABC 关于直线 MN 对称.
A
B
C
M
N
A
B
C
M
N
A′
B′
C′
A′
C′
B′
规律总结
(1)若某点在对称轴上,则它的对称点也一定在对称轴上,并且和这个点重合.
(2)如果一个点在对称轴的左侧,那么这个点的对称点一定在对称轴的右侧.
4.如图,在网格中有两个大小、形状一样的图形(阴影部分),用这两个图形拼成轴对称图形,试分别在图中画出两种不同的拼法.
10.1 轴对称
第4课时 设计轴对称图案
华东师大版数学七年级下册
第10章 轴对称、平移与旋转
新课导入
为什么它们总给我们美的感觉?
人类在漫长的岁月中体验着对称,享受着对称,它给人以平衡与和谐的美感.今天这节课要求发挥大家的想象力自己去设计对称图案,自己去创造对称美.
下面是一个轴对称图形.
(1)有多少条对称轴呢
(2)可以利用轴对称来画出它吗
推进新课
准备一张正方形纸片,按以下五个步骤一起来画:
(1)在正方形纸片上用虚线画出四条对称轴.
(2)如图,在其中一个三角形中,画出图形形状的基本线条(可以自己设计线条).
(3)按照其中一条斜的对称轴画出(2)中图形的对称图形.
(4)按照其中一条斜的对称轴画出(3)中图形的对称图形.
(5)按照水平(或垂直)对称轴画出(4)中图形的对称图形.
画好后可以涂上自己喜欢的颜色,擦掉其它多余的线条,一幅对称的图案就完成了(如下图).
归纳设计对称图案的步骤:
(1)画出对称轴
(2)画出图形的基本形状的部分线条
(3)按照其中一条对称轴画出基本形状的对称图形
(4)按照另一条对称轴继续画对称图形
(5)完成对称图案设计
随堂练习
1.用四块如图的瓷砖拼成一个正方形,形成轴对称的图案,和自己的同伴比一比,看谁的拼法多.
2. 请你利用一个等腰三角形、2个长方形、3个圆设计一个轴对称图形,并用简练的文字说明你的创意.
天平
3.仿照课文的过程,利用下图设计出一个轴对称图案.
谢谢观看
10.1 轴对称
第1课时 生活中的轴对称
华东师大版数学七年级下册
第10章 轴对称、平移与旋转
新课导入
观察下列图片说说你有何发现?
这些美丽的图形来自生活,你能发现这些图形有什么共同特征吗?用自己的语言描述.
自远古以来,对称形式被认为是和谐、美丽的.不论在自然界里还是在建筑中,不论在艺术中还是在科学中,甚至最普通的日常生活用品中,对称的形式都随处可见.
生活中的轴对称
拱桥
埃菲尔铁塔
思 考
你能不能在下面的图形中画一条线,再把这个图形沿你所画的线对折,使左右两旁的部分完全重合.
如果一个图形沿某条直线对折后,直线两旁的部分能够_________,那么这个图形叫做轴对称图形.
轴对称图形的定义
完全重合
这条直线叫这个图形的对称轴.
练 习
找出图中各图形的对称轴. 是否有些图形的对称轴不止一条呢?
判断一个图形为轴对称图形方法:
(1)沿某条直线对折;
(2)直线两旁的部分能够完全重合.
轴对称
观察下面两组图形.
想一想 当把这两个天使沿着一条直线折叠后,会发现什么样的现象?
沿着一条直线折叠后,这两个五边形会有什么现象?
像这样,把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称.
这条直线就是对称轴.
两个图形的对应点(即两个图形重合时互相重合的点)叫做对称点.
你能举出生活中两个图形成轴对称的例子吗?
说一说
日常生活中,我们经常会照镜子,而镜子中的像与本人就关于镜面成轴对称.
做一做
请你标出图中A、B、C三点的对称点A1、B1、C1.
A
B
C
A1
B1
C1
轴对称图形(或成轴对称的两个图形)沿对称轴对折后的两部分是完全重合的,所以它的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
轴对称图形的基本特征
剪纸艺术
随堂练习
1.下列图形中,一定是轴对称图形的是( )
A.锐角三角形 B.曲线
C.线段 D.直角三角形
C
2. 等腰三角形的对称轴有( )
A.一条 B.二条
C.三条 D.一条或三条
D
3.如图,哪一个选项中的右边图形与左边图形成轴对称( )
A
B
C
D
C
4.下列交通标志中哪些是轴对称图形?
×
√
×
√
10.1 轴对称
第2课时 轴对称的再认识
华东师大版数学七年级下册
第10章 轴对称、平移与旋转
新课导入
观察线段和角,它们都是轴对称图形吗?
A
B
O
C
D
把一个图形沿某条直线对折,对折后的两部分能完全重合,这样的图形称为轴对称图形.
什么是轴对称图形?
新课推进
在纸上画出线段AB及它的中点O,再过O点画与AB垂直的直线CD,沿直线CD将纸对折,观察线段OA和线段OB是否重合?
A
B
O
C
D
在上述试验中,显然线段OA和线段OB互相重合,因此,线段AB是轴对称图形.
A
B
O
C
D
垂直并且平分一条线段的直线称为这条线段的垂直平分线.
A
B
O
C
D
上图中直线CD是线段AB的垂直平分线. 线段的垂直平分线是一条直线.
垂直平分线又可称为中垂线.
线段的对称轴是什么?它是唯一的吗?
思 考
线段的对称轴有两条,一条是它的垂直平分线所在的直线,另一条是这条线段所在的直线.
A
B
在纸上画一个角∠AOB,然后对折这个角,使角的两条边完全重合,然后用直尺画出折痕OM. 看看射线OM与∠AOB是什么关系.
试一试
O
A
B
M
O
A
B
M
角是轴对称图形,对称轴是它的角平分线所在的直线.
有时我们感觉一个图形是轴对称的,那么如何来验证呢?这就需要我们去找到它的对称轴,看看沿着对称轴翻折以后两部分是否重合.
如图,方格纸内的两图形都是轴对称图形,请画出它们的对称轴.
试一试
在上图中,由于图形在方格纸内,我们可以凭直觉很准确地画出两个图形的对称轴,你能想想是什么原因吗?
因为在方格纸中我们比较容易看清楚图形的位置,也就比较容易确定图形的中间位置.
如果没有方格纸,而又不能折叠,你还能比较容易地画出图形的对称轴吗?请同学试试看,如下图的对称轴我们应该如何去画呢?
(1)
(2)
如图点 A 和点 A′ 关于某直线对称,你能画出这条直线吗?
做一做
A
A′
l
如图,连结点 A 和点 A′,画出线段 AA′ 的垂直平分线 l,则直线 l 就是所是点 A 和点 A′ 的对称轴.
A
A′
l
总 结
轴对称图形对称轴的画法:
1.找出轴对称图形的任意一组对称点,连结对称点.
2.画出连接对称点的线段的垂直平分线.则这条垂直平分线就是它的对称轴.
如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
随堂练习
1.下列说法错误的是( )
A.等边三角形是轴对称图形
B.轴对称图形的对应边相等,对应角相等
C.成轴对称的两条线段必在对称轴一侧
D.成轴对称的两个图形对应点的连线被对称轴垂直平分
C
2.下面的一些虚线,哪些是图形对称轴,哪些不是图形的对称轴?
②④⑥是图形的对称轴
3.已知,直线 a 与直线 b 是两条相交直线,它是轴对称图形吗?如果是,它有几条对称轴?画图试试看.
a
b
是轴对称图形,有2条对称轴.
4. 画出以下图形的对称轴.
10.1 轴对称
第3课时 画轴对称图形
华东师大版数学七年级下册
第10章 轴对称、平移与旋转
新课导入
上节课我们学习了画两个图形或一个图形的对称轴.请同学们为下面的两张轴对称图形画出对称轴.
将画好的轴对称图形遮掉左边一半或右边一半后,你能还原出原来的图形来吗?
想一想
如果给出一个图形和一条直线,那么如何画出这个图形关于这条直线的对称图形呢?
新课推进
如图,实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形.
试一试
A
B
C
A′
B′
C′
画完之后,请同学们思考下面两个问题:
(1)你可以通过什么方法来验证你画得是否正确.
(2)和其他同学比较一下,你的方法是最简单吗?
在格点图中,大家会很容易画出已知图形的轴对称图形,如果没有格点,你还能比较准确地画出已知图形的轴对称图形吗?
如图,已知点 A 和直线 l ,试画出点 A 关于直线 l 的对称点 A′.
做一做
(1)过点 A 向直线 l 画垂线段 AO,垂足点 O;
(2)延长AO至OA′,使OA′ = OA.则点 A′ 就是点 A关于直线 l 的对称点.
A
l
O
A′
你能画出线段 AB 关于直线 l 的对称线段吗?
练 习
l
(1)画点A、点B关于直线l的对称点A′ 、B′;
(2)连结A′、B′ .
则线段 A′B′ 就是线段AB关于直线 l 的对称线段.
A
B
A′
B′
例 已知△ABC,直线 l,画出△ABC关于直线 l 对称的图形.
l
A
B
C
A′
B′
C′
(1)分别画出点A、B 和 C 点关于直线 l 的对称点A′、B′ 和 C′;
(2)连结 A′B′、B′C′、A′C′、则△A′B′C′ 就是△ABC关于直线 l 的对称三角形.
步 骤
从上面的例子可以知道,如果图形是由直线、线段或射线组成时,那么只要画出图形中的特殊点的对称点,然后连接对称点,就可以画出关于这条直线的对称图形.
随堂练习
1.下列各图都是一个汉字的一半,你能想像出它的另一半并能确定它是什么字吗 (有几个字的笔划在对称轴上.)
品
口
来
晶
品
口
来
晶
2. 如图,作字母 M 关于 y 轴的轴对称图形并写出所得图形相应各端点的坐标.
x
y
A
B(-4,3)
C(-2.5,0)
D(-1,3)
E
E1
C1(2.5,0)
A1
B1(4,3)
D1(1,3)
3.如图,已知△ABC 和直线 MN. 求作△A′B′C′,使△A′B′C′ 和 △ABC 关于直线 MN 对称.
A
B
C
M
N
A
B
C
M
N
A′
B′
C′
A′
C′
B′
规律总结
(1)若某点在对称轴上,则它的对称点也一定在对称轴上,并且和这个点重合.
(2)如果一个点在对称轴的左侧,那么这个点的对称点一定在对称轴的右侧.
4.如图,在网格中有两个大小、形状一样的图形(阴影部分),用这两个图形拼成轴对称图形,试分别在图中画出两种不同的拼法.
10.1 轴对称
第4课时 设计轴对称图案
华东师大版数学七年级下册
第10章 轴对称、平移与旋转
新课导入
为什么它们总给我们美的感觉?
人类在漫长的岁月中体验着对称,享受着对称,它给人以平衡与和谐的美感.今天这节课要求发挥大家的想象力自己去设计对称图案,自己去创造对称美.
下面是一个轴对称图形.
(1)有多少条对称轴呢
(2)可以利用轴对称来画出它吗
推进新课
准备一张正方形纸片,按以下五个步骤一起来画:
(1)在正方形纸片上用虚线画出四条对称轴.
(2)如图,在其中一个三角形中,画出图形形状的基本线条(可以自己设计线条).
(3)按照其中一条斜的对称轴画出(2)中图形的对称图形.
(4)按照其中一条斜的对称轴画出(3)中图形的对称图形.
(5)按照水平(或垂直)对称轴画出(4)中图形的对称图形.
画好后可以涂上自己喜欢的颜色,擦掉其它多余的线条,一幅对称的图案就完成了(如下图).
归纳设计对称图案的步骤:
(1)画出对称轴
(2)画出图形的基本形状的部分线条
(3)按照其中一条对称轴画出基本形状的对称图形
(4)按照另一条对称轴继续画对称图形
(5)完成对称图案设计
随堂练习
1.用四块如图的瓷砖拼成一个正方形,形成轴对称的图案,和自己的同伴比一比,看谁的拼法多.
2. 请你利用一个等腰三角形、2个长方形、3个圆设计一个轴对称图形,并用简练的文字说明你的创意.
天平
3.仿照课文的过程,利用下图设计出一个轴对称图案.
谢谢观看
