数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系(共27张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.1直线与圆的位置关系(共27张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 16:30:20 | ||
图片预览







文档简介
(共27张PPT)
2.5.1
直线与圆的位置关系
情景导入
“海上生明月,天涯共此时”,这是唐代诗人张九龄的诗句。
从诗句中所反映的景象可以联想出哪些基本的几何图形呢?
它们有哪些位置关系呢?
新知初探
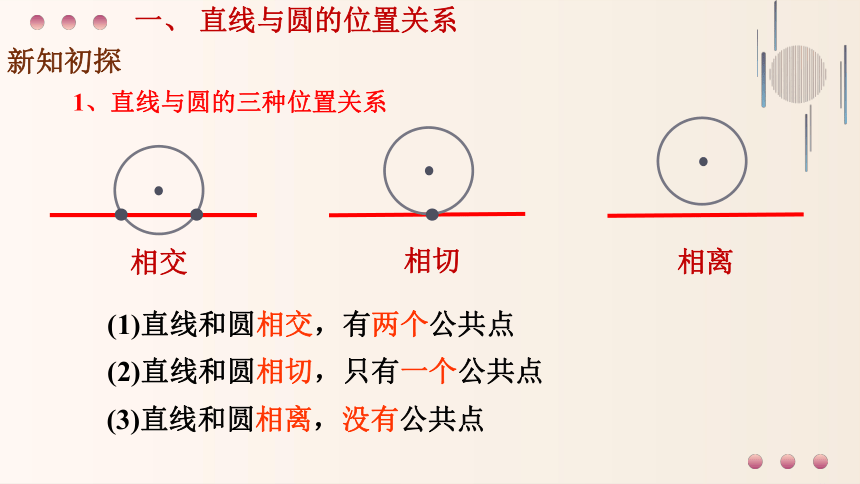
相交
相切
相离
一、 直线与圆的位置关系
1、直线与圆的三种位置关系
(2)直线和圆相切,只有一个公共点
(1)直线和圆相交,有两个公共点
(3)直线和圆相离,没有公共点
一、 直线与圆的位置关系
2、直线与圆的位置关系的判断方法
(1)回顾两直线的位置关系的判断方法
我们是通过联立两直线方程,求出解的个数来确定两直线的位置关系。
类似我们也可以通过联立直线与圆的方程求出解的个数来判断直线与圆的位置关系。
复习回顾
典例精析
1、已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
消去y,得:
思路1:
联立方程组:
代数法
x2-3x+2=0
消元(消x或y)
计算△(或直接求根)
判断符号(或根的个数)
得出结论
联立方程组
代数法的基本步骤:
∵△=(-3)2-4×1×2=1>0
∴有两个公共点,直线l与圆相交
解得:x1=1,x2=2
∴直线l与圆相交,有两个公共点
典例精析
1、已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
代数法
如果相交,求直线l被圆C所截得的弦长
消去y,得:
思路1:
联立方程组:
x2-3x+2=0
∵△=(-3)2-4×1×2=1>0
∴有两个公共点,直线l与圆相交
解得:x1=1,x2=2
∴直线l与圆相交,有两个公共点
把x1=1,x2=2分别代入方程①,得y1=3,y2=0
∴直线l与圆C的两个交点是A(1,3),B(2,0).
复习回顾
一、 直线与圆的位置关系
2、直线与圆的位置关系的判断方法
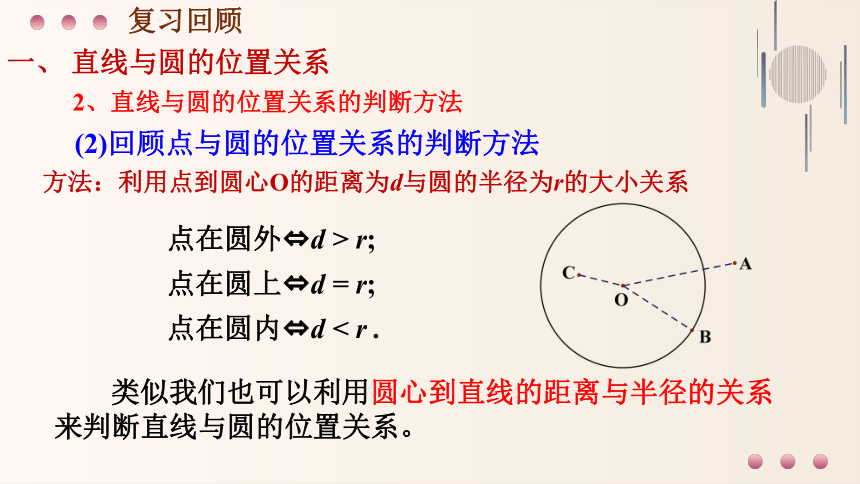
(2)回顾点与圆的位置关系的判断方法
方法:利用点到圆心O的距离为d与圆的半径为r的大小关系
点在圆外 d > r;
点在圆上 d = r;
点在圆内 d < r .
类似我们也可以利用圆心到直线的距离与半径的关系来判断直线与圆的位置关系。
典例精析
1、已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
思路2:
几何法
将圆方程化为标准式为:x2+(y-1)2=5
∴圆心坐标为(0,1),半径为
圆心到直线l的距离
∴直线l与圆相交,有两个公共点.
.
x
y
O
C
A
B
l
几何法的基本步骤:
计算弦心距d
比较d,r
得出结论.
求圆心坐标和半径r
典例精析
1、已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
思路2:
几何法
将圆方程化为标准式为:x2+(y-1)2=5
∴圆心坐标为(0,1),半径为
圆心到直线l的距离
∴直线l与圆相交,有两个公共点.
如果相交,求直线l被圆C所截得的弦长
.
x
y
O
C
A
B
l
2、几何法:计算圆心到直线的距离d,与半径r相比较
运算量较大
请谨慎选择
方法总结
判断直线与圆的位置关系的方法
1、代数法:由 消元得一元二次方程的判别式△
△>0 相交;△=0 相切;△<0 相离.
d < r 相交;d = r 相切;d > r 相离.
随堂练习
1、判断下列各组直线l与圆C的位置关系
(1)l:x-y+1=0 圆C:x2+y2=3
(2)l:3x+4y+2=0 圆C:x2+y2-2x=0
(3)l:x+y+3=0 圆C:x2+y2+2x=0
2、判断直线2x-y+2=0与圆(x-1)2+(y-2)2=4的位置关系;如果相交,求出直线被圆截得的弦长.
相交
相切
相离
直线与圆相交,弦长为
典例精析
2、过点P(2,1)作圆O:x2+y2 =1的切线l,求切线l的方程。
二、直线与圆的位置关系综合应用——切线问题
x=2
法一:
由圆心(0,0)到切线l的距离等于圆的半径1,得
解:由题意可知,斜率存在,
设切线l的斜率为k,则l的切线方程为y-1=k(x-2),即kx-y+1-2k=0
因此,所求切线l的方程为y=1或4x-3y-5=0
几何法
典例精析
2、过点P(2,1)作圆O:x2+y2 =1的切线l,求切线l的方程。
二、直线与圆的位置关系综合应用——切线问题
x=2
法二:
解:由题意可知,斜率存在,
设切线l的斜率为k,则l的切线方程为y-1=k(x-2),即kx-y+1-2k=0
代数法
因为直线l与圆相切,所以方程组
只有一组解.
消元,得(k2+1)x2+(2k-4k2)x+4k2-4k=0
因为方程只有一组解,所以
△=(2k-4k2)2-4(k2+1)(4k2-4k)=0
因此,所求切线l的方程为y=1或4x-3y-5=0
随堂练习
3、过点(1,2)作圆O:x2+y2=1的切线l,求此切线l的方程.
解:点P在圆外,所以过P有两条切线。
即kx-y+2-k=0
由圆心(0,0)到切线l的距离等于圆的半径1,得
设切线l的方程为y-2=k(x-1),
此时,切线l的方程为3x-4y+5=0.
∵直线x=1也符合题意.
故切线l的方程为:x=1 或3x-4y+5=0.
随堂练习
4、过点P(1,2)作圆O:x2+y2=5的切线l,求此切线l的方程.
解:依题意,切线斜率存在,可设斜率为k,
所以直线l的方程为:x+2y-5=0
∵l⊥OP,kOP=2
随堂练习
5、过点P(1,1)作圆O:x2+y2=5的切线l,求此切线l的方程.
不存在切线
规律方法
2、过圆外一点(x0,y0)的圆的切线方程的求法
几何法:设切线方程为y-y0=k(x-x0).由圆心到直线的距离等于半径,可求得k,也就得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程x=x0或y=y0.
1、过圆上一点的圆的切线方程的求法
几何法:求过圆上一点(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,再由垂直关系得切线的斜率为 ,由点斜式可得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程x=x0或y=y0.
圆的切线方程的求法
代数法(一般不用):设切线方程为y-y0=k(x-x0),与圆的方程联立,消去y后得到关于x的一元二次方程,由Δ=0求出k,可得切线方程.
随堂练习
6、(2023年全国Ⅰ卷第6题)过点(0,-2)与圆x2+y2-4x-1=0相切的两条直线的夹角为α,则sinα=( )
解析:圆x2+y2-4x-1=0可化为圆(x-2)2+y2=5,
设P(0,-2),切线为PA,PB,切点为A,B,
B
随堂练习
7、直线x+y=1与圆x2+y2-2ay=0(a>0)没有公共点,则a的取值范围是 .
由题意得圆心(0,a)到直线x+y-1=0的距离大于半径a,即
解得 ,又a>0,∴
变式1:若有一个公共点呢?
变式2:若有两个公共点呢?
变式3:若去掉条件a>0,结果又如何?(课后思考)。
随堂练习
8、直线y=x-1上的点与圆x2+y2+4x-2y+4=0上的点的距离的最小值为( )
C
解:圆x2+y2+4x-2y+4=0的圆心为(-2,1),半径为1,
圆心到直线y=x-1的距离为
所以直线y=x-1上的点与圆x2+y2+4x-2y+4=0上的点的距离的最小值为 .
随堂练习
9、自点A(-3,3)发射的光线l 射到x轴上,被x轴反射,其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切,求反射光线所在直线的方程
A(-3,3)
C(2, 2)
A′(-3,-3)
C′(2, -2)
l : 4x+3y+3=0或3x+4y-3=0
x
y
3、如图是某圆拱桥的一孔圆拱的示意图. 该圆拱跨度AB=20米,拱高OP=4米,在建造时每隔4米需要用一个支柱支撑,求支柱A2P2的长度(精确到0.01m)
由方程组
答:支柱A2P2的长度约为3.86米
把点P2的横坐标x=-2代入这个圆的方程,得y=3.86(y>0)
下面用待定系数法来确定b和r的值.
x2+(y–b)2=r2
因为P、B都在圆上,所以它们的坐标(0,4)、(10,0)满足方程
解得:b=-10.5 r2=14.52
所以圆的方程为: x2+(y+10.5)2=14.52
解:如图建立平面直角坐标系,圆心在y轴上,设圆心的坐标是(0,b),圆的半径是r,那么圆的方程是
典例精析
A
B
A1
A2
A3
A4
O
P
P2
x
y
典例精析
.
轮船航线所在直线l的方程为:
问题归结为圆心为O的圆与直线l有无公共点.
解:以小岛中心为原点O,东西方向为x轴,建立如图所示的直角坐标系,其中取10km为单位长度,则港口所在位置的坐标为(0,3),轮船所在位置的坐标为(4,0)
这样,受暗礁影响的圆形区域所对应的圆心为O的圆的方程为:
O
x
y
港口
.
轮船
(4, 0)
(0, 3)
(2, 0)
4、一个小岛的周围有环岛暗礁,暗礁分布在以小岛的中心为圆心,半径为20km的圆形区域.已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处.如果轮船沿直线返港,那么它是否会有触礁的危险?
x2+y2=4
圆心O到直线l的距离d
所以直线l与圆O相离,轮船沿直线返港不会有触礁危险
.
规律方法
坐标法解决平面几何问题的“三步曲”:
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
第一步 :建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
用坐标法解决几何问题时,先用坐标和方程表示相应的几何元素:点、直线、圆,将几何问题转化为代数问题;然后通过代数运算解决代数问题;最后解释代数运算结果的几何含义,得到几何问题的结论.
课堂总结
1、判断直线和圆的位置关系
几何方法
求圆心坐标及半径r
圆心到直线的距离d
代数方法
消去y(或x)
联消算判结
求算比结
△>0 相交;
△=0 相切;
△<0 相离.
d < r 相交;
d = r 相切;
d > r 相离.
px2+qx-t=0
课堂总结
2、求过一点P的圆的切线方程问题需注意:
(1)先判断点P与圆的位置关系
(2)应用待定系数法设直线方程时,要注意斜率不存在的情况。
若点P在圆上,切线有一条
若点P在圆外,切线有两条
若点P在圆内,没有切线
知识
与
方法
核心素养
数学思想
3种
关系
两种
方法
数学
运算
逻辑推理
直观想象
函数与方程
数形结合
化归与转化
畅谈收获
独立思考
2.5.1
直线与圆的位置关系
情景导入
“海上生明月,天涯共此时”,这是唐代诗人张九龄的诗句。
从诗句中所反映的景象可以联想出哪些基本的几何图形呢?
它们有哪些位置关系呢?
新知初探
相交
相切
相离
一、 直线与圆的位置关系
1、直线与圆的三种位置关系
(2)直线和圆相切,只有一个公共点
(1)直线和圆相交,有两个公共点
(3)直线和圆相离,没有公共点
一、 直线与圆的位置关系
2、直线与圆的位置关系的判断方法
(1)回顾两直线的位置关系的判断方法
我们是通过联立两直线方程,求出解的个数来确定两直线的位置关系。
类似我们也可以通过联立直线与圆的方程求出解的个数来判断直线与圆的位置关系。
复习回顾
典例精析
1、已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
消去y,得:
思路1:
联立方程组:
代数法
x2-3x+2=0
消元(消x或y)
计算△(或直接求根)
判断符号(或根的个数)
得出结论
联立方程组
代数法的基本步骤:
∵△=(-3)2-4×1×2=1>0
∴有两个公共点,直线l与圆相交
解得:x1=1,x2=2
∴直线l与圆相交,有两个公共点
典例精析
1、已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
代数法
如果相交,求直线l被圆C所截得的弦长
消去y,得:
思路1:
联立方程组:
x2-3x+2=0
∵△=(-3)2-4×1×2=1>0
∴有两个公共点,直线l与圆相交
解得:x1=1,x2=2
∴直线l与圆相交,有两个公共点
把x1=1,x2=2分别代入方程①,得y1=3,y2=0
∴直线l与圆C的两个交点是A(1,3),B(2,0).
复习回顾
一、 直线与圆的位置关系
2、直线与圆的位置关系的判断方法
(2)回顾点与圆的位置关系的判断方法
方法:利用点到圆心O的距离为d与圆的半径为r的大小关系
点在圆外 d > r;
点在圆上 d = r;
点在圆内 d < r .
类似我们也可以利用圆心到直线的距离与半径的关系来判断直线与圆的位置关系。
典例精析
1、已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
思路2:
几何法
将圆方程化为标准式为:x2+(y-1)2=5
∴圆心坐标为(0,1),半径为
圆心到直线l的距离
∴直线l与圆相交,有两个公共点.
.
x
y
O
C
A
B
l
几何法的基本步骤:
计算弦心距d
比较d,r
得出结论.
求圆心坐标和半径r
典例精析
1、已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4 =0,判断直线l与圆C的位置关系。
思路2:
几何法
将圆方程化为标准式为:x2+(y-1)2=5
∴圆心坐标为(0,1),半径为
圆心到直线l的距离
∴直线l与圆相交,有两个公共点.
如果相交,求直线l被圆C所截得的弦长
.
x
y
O
C
A
B
l
2、几何法:计算圆心到直线的距离d,与半径r相比较
运算量较大
请谨慎选择
方法总结
判断直线与圆的位置关系的方法
1、代数法:由 消元得一元二次方程的判别式△
△>0 相交;△=0 相切;△<0 相离.
d < r 相交;d = r 相切;d > r 相离.
随堂练习
1、判断下列各组直线l与圆C的位置关系
(1)l:x-y+1=0 圆C:x2+y2=3
(2)l:3x+4y+2=0 圆C:x2+y2-2x=0
(3)l:x+y+3=0 圆C:x2+y2+2x=0
2、判断直线2x-y+2=0与圆(x-1)2+(y-2)2=4的位置关系;如果相交,求出直线被圆截得的弦长.
相交
相切
相离
直线与圆相交,弦长为
典例精析
2、过点P(2,1)作圆O:x2+y2 =1的切线l,求切线l的方程。
二、直线与圆的位置关系综合应用——切线问题
x=2
法一:
由圆心(0,0)到切线l的距离等于圆的半径1,得
解:由题意可知,斜率存在,
设切线l的斜率为k,则l的切线方程为y-1=k(x-2),即kx-y+1-2k=0
因此,所求切线l的方程为y=1或4x-3y-5=0
几何法
典例精析
2、过点P(2,1)作圆O:x2+y2 =1的切线l,求切线l的方程。
二、直线与圆的位置关系综合应用——切线问题
x=2
法二:
解:由题意可知,斜率存在,
设切线l的斜率为k,则l的切线方程为y-1=k(x-2),即kx-y+1-2k=0
代数法
因为直线l与圆相切,所以方程组
只有一组解.
消元,得(k2+1)x2+(2k-4k2)x+4k2-4k=0
因为方程只有一组解,所以
△=(2k-4k2)2-4(k2+1)(4k2-4k)=0
因此,所求切线l的方程为y=1或4x-3y-5=0
随堂练习
3、过点(1,2)作圆O:x2+y2=1的切线l,求此切线l的方程.
解:点P在圆外,所以过P有两条切线。
即kx-y+2-k=0
由圆心(0,0)到切线l的距离等于圆的半径1,得
设切线l的方程为y-2=k(x-1),
此时,切线l的方程为3x-4y+5=0.
∵直线x=1也符合题意.
故切线l的方程为:x=1 或3x-4y+5=0.
随堂练习
4、过点P(1,2)作圆O:x2+y2=5的切线l,求此切线l的方程.
解:依题意,切线斜率存在,可设斜率为k,
所以直线l的方程为:x+2y-5=0
∵l⊥OP,kOP=2
随堂练习
5、过点P(1,1)作圆O:x2+y2=5的切线l,求此切线l的方程.
不存在切线
规律方法
2、过圆外一点(x0,y0)的圆的切线方程的求法
几何法:设切线方程为y-y0=k(x-x0).由圆心到直线的距离等于半径,可求得k,也就得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程x=x0或y=y0.
1、过圆上一点的圆的切线方程的求法
几何法:求过圆上一点(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,再由垂直关系得切线的斜率为 ,由点斜式可得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程x=x0或y=y0.
圆的切线方程的求法
代数法(一般不用):设切线方程为y-y0=k(x-x0),与圆的方程联立,消去y后得到关于x的一元二次方程,由Δ=0求出k,可得切线方程.
随堂练习
6、(2023年全国Ⅰ卷第6题)过点(0,-2)与圆x2+y2-4x-1=0相切的两条直线的夹角为α,则sinα=( )
解析:圆x2+y2-4x-1=0可化为圆(x-2)2+y2=5,
设P(0,-2),切线为PA,PB,切点为A,B,
B
随堂练习
7、直线x+y=1与圆x2+y2-2ay=0(a>0)没有公共点,则a的取值范围是 .
由题意得圆心(0,a)到直线x+y-1=0的距离大于半径a,即
解得 ,又a>0,∴
变式1:若有一个公共点呢?
变式2:若有两个公共点呢?
变式3:若去掉条件a>0,结果又如何?(课后思考)。
随堂练习
8、直线y=x-1上的点与圆x2+y2+4x-2y+4=0上的点的距离的最小值为( )
C
解:圆x2+y2+4x-2y+4=0的圆心为(-2,1),半径为1,
圆心到直线y=x-1的距离为
所以直线y=x-1上的点与圆x2+y2+4x-2y+4=0上的点的距离的最小值为 .
随堂练习
9、自点A(-3,3)发射的光线l 射到x轴上,被x轴反射,其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切,求反射光线所在直线的方程
A(-3,3)
C(2, 2)
A′(-3,-3)
C′(2, -2)
l : 4x+3y+3=0或3x+4y-3=0
x
y
3、如图是某圆拱桥的一孔圆拱的示意图. 该圆拱跨度AB=20米,拱高OP=4米,在建造时每隔4米需要用一个支柱支撑,求支柱A2P2的长度(精确到0.01m)
由方程组
答:支柱A2P2的长度约为3.86米
把点P2的横坐标x=-2代入这个圆的方程,得y=3.86(y>0)
下面用待定系数法来确定b和r的值.
x2+(y–b)2=r2
因为P、B都在圆上,所以它们的坐标(0,4)、(10,0)满足方程
解得:b=-10.5 r2=14.52
所以圆的方程为: x2+(y+10.5)2=14.52
解:如图建立平面直角坐标系,圆心在y轴上,设圆心的坐标是(0,b),圆的半径是r,那么圆的方程是
典例精析
A
B
A1
A2
A3
A4
O
P
P2
x
y
典例精析
.
轮船航线所在直线l的方程为:
问题归结为圆心为O的圆与直线l有无公共点.
解:以小岛中心为原点O,东西方向为x轴,建立如图所示的直角坐标系,其中取10km为单位长度,则港口所在位置的坐标为(0,3),轮船所在位置的坐标为(4,0)
这样,受暗礁影响的圆形区域所对应的圆心为O的圆的方程为:
O
x
y
港口
.
轮船
(4, 0)
(0, 3)
(2, 0)
4、一个小岛的周围有环岛暗礁,暗礁分布在以小岛的中心为圆心,半径为20km的圆形区域.已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处.如果轮船沿直线返港,那么它是否会有触礁的危险?
x2+y2=4
圆心O到直线l的距离d
所以直线l与圆O相离,轮船沿直线返港不会有触礁危险
.
规律方法
坐标法解决平面几何问题的“三步曲”:
第二步:通过代数运算,解决代数问题;
第三步:将代数运算结果“翻译”成几何结论.
第一步 :建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
用坐标法解决几何问题时,先用坐标和方程表示相应的几何元素:点、直线、圆,将几何问题转化为代数问题;然后通过代数运算解决代数问题;最后解释代数运算结果的几何含义,得到几何问题的结论.
课堂总结
1、判断直线和圆的位置关系
几何方法
求圆心坐标及半径r
圆心到直线的距离d
代数方法
消去y(或x)
联消算判结
求算比结
△>0 相交;
△=0 相切;
△<0 相离.
d < r 相交;
d = r 相切;
d > r 相离.
px2+qx-t=0
课堂总结
2、求过一点P的圆的切线方程问题需注意:
(1)先判断点P与圆的位置关系
(2)应用待定系数法设直线方程时,要注意斜率不存在的情况。
若点P在圆上,切线有一条
若点P在圆外,切线有两条
若点P在圆内,没有切线
知识
与
方法
核心素养
数学思想
3种
关系
两种
方法
数学
运算
逻辑推理
直观想象
函数与方程
数形结合
化归与转化
畅谈收获
独立思考
