2..2..3直线与平面平行性质(2课时)
文档属性
| 名称 | 2..2..3直线与平面平行性质(2课时) |  | |
| 格式 | rar | ||
| 文件大小 | 439.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-04 07:14:00 | ||
图片预览



文档简介
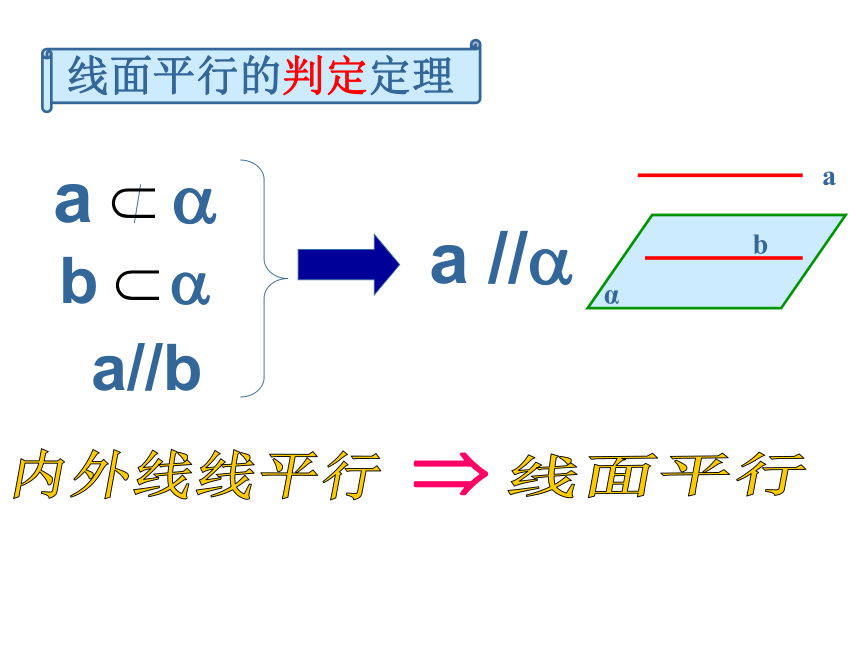
课件16张PPT。直线与平面平行的性质定理aαb线面平行的判定定理内外线线平行a //?a//b
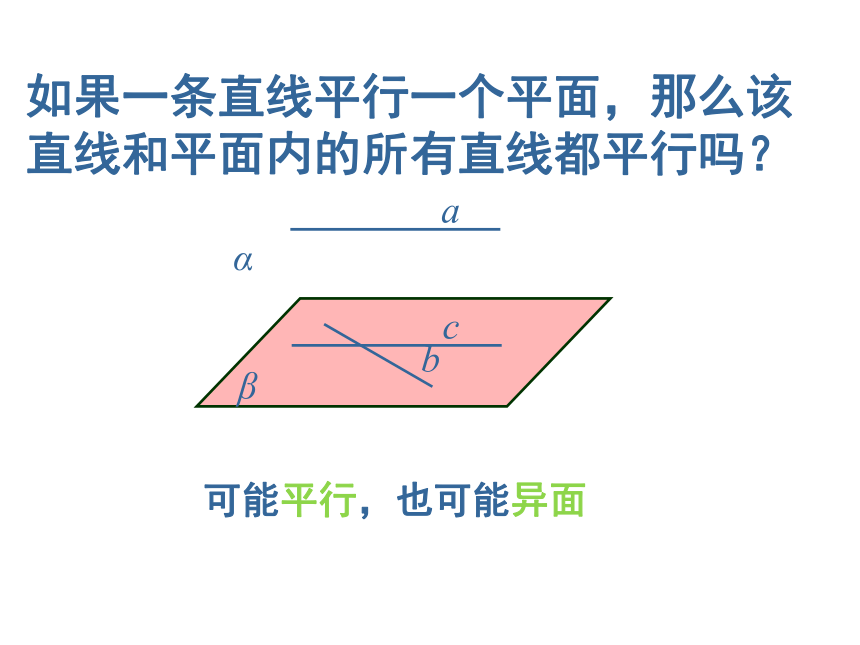
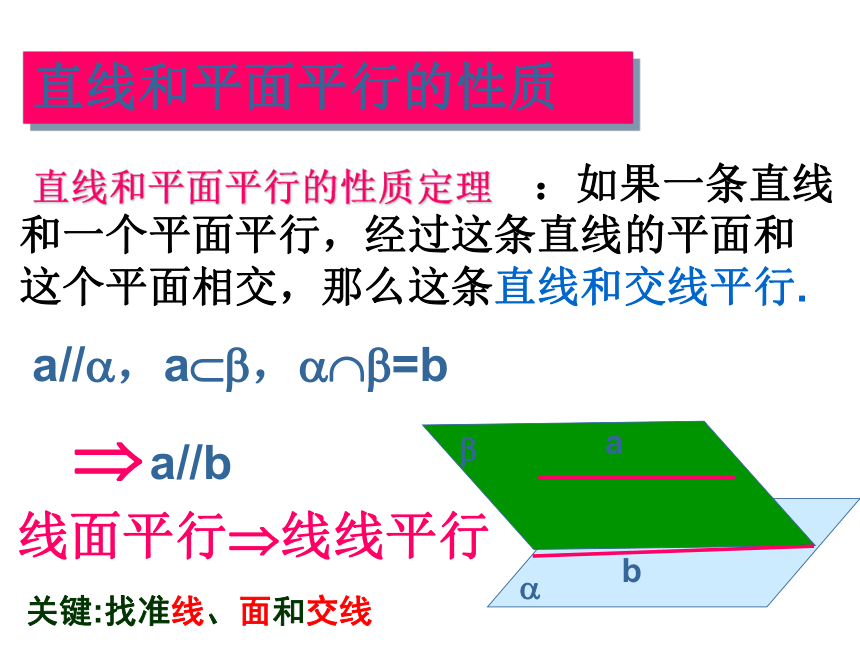
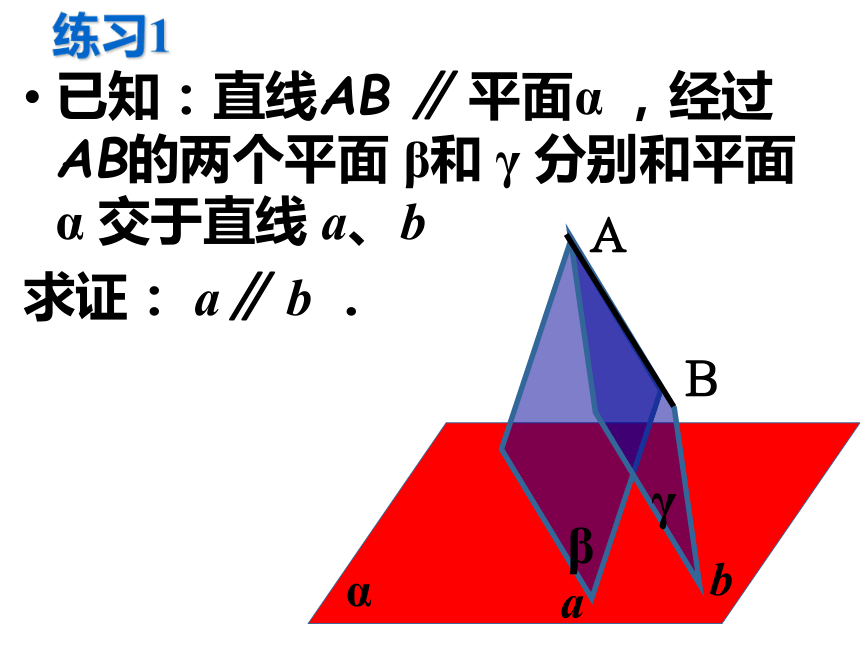
直线和平面平行又有什么性质呢?α β 如果一条直线平行一个平面,那么该直线和平面内的所有直线都平行吗?可能平行,也可能异面 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线 . 证明:直线和平面平行的性质 :如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.直线和平面平行的性质定理a//?,a??,???=b线面平行?线线平行? a//b 关键:找准线、面和交线 练习1已知:直线AB ∥ 平面α ,经过AB的两个平面 β和 γ 分别和平面α 交于直线 a、b
求证: a∥ b .ABab延伸练习2已知:直线AB∥ 平面 α ,
AC∥BD且AC、BD与平面 α 相交
于点C、D, 求证:AC=BD 证明:连结CD ∵ AC ∥ BD
∴ AC 、BD确定平面AD
则AB 平面AD,平面AD ∩ α =CD
∵直线AB ∥ 平面 α
∴ AB ∥CD ,
∴四边形ABCD是平行四边形
∴ AC=BD ∩ abcαβ 证明:过a 作平面β交平面α于直线 c 例1、已知直线 a∥直线b,直线
a∥平面α, b α,求证:b∥平面α练习3、 若一直线与两个相交平面都平行,则这条直线与两平面的交线平行。例2: 在图中所示的一块木料中,
棱 平行于面 .
(1)要经过面 内的一点
和棱 将木料据开,应怎样画线?
(2)所画的线和 面 是什么位置关系?演示课件 练习:已知空间四边形ABCD被一平面所截,
截面EFGH是一个平行四边形,
求证:CD∥平面EFGHABCDFEHG证明 ∵ 四边形EFGH是平行四边形
∴EF∥GH∵GH 平面BCD
EF 平面BCD平面BCD∩平面ACD=CD∴EF∥平面BCD∵EF 平面ACD∴EF∥CD∵EF 平面EFGH CD 平面EFGH∴CD∥平面EFGH线线平行 线面平行判定定理性质定理判断线面平行判断线线平行对比小结 归纳小结: 1.主题:线面平行的性质定理 内容:线面平行则内外直线平行 关键:过已知线找(作)面与已知面相交
直线和平面平行又有什么性质呢?α β 如果一条直线平行一个平面,那么该直线和平面内的所有直线都平行吗?可能平行,也可能异面 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线 . 证明:直线和平面平行的性质 :如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.直线和平面平行的性质定理a//?,a??,???=b线面平行?线线平行? a//b 关键:找准线、面和交线 练习1已知:直线AB ∥ 平面α ,经过AB的两个平面 β和 γ 分别和平面α 交于直线 a、b
求证: a∥ b .ABab延伸练习2已知:直线AB∥ 平面 α ,
AC∥BD且AC、BD与平面 α 相交
于点C、D, 求证:AC=BD 证明:连结CD ∵ AC ∥ BD
∴ AC 、BD确定平面AD
则AB 平面AD,平面AD ∩ α =CD
∵直线AB ∥ 平面 α
∴ AB ∥CD ,
∴四边形ABCD是平行四边形
∴ AC=BD ∩ abcαβ 证明:过a 作平面β交平面α于直线 c 例1、已知直线 a∥直线b,直线
a∥平面α, b α,求证:b∥平面α练习3、 若一直线与两个相交平面都平行,则这条直线与两平面的交线平行。例2: 在图中所示的一块木料中,
棱 平行于面 .
(1)要经过面 内的一点
和棱 将木料据开,应怎样画线?
(2)所画的线和 面 是什么位置关系?演示课件 练习:已知空间四边形ABCD被一平面所截,
截面EFGH是一个平行四边形,
求证:CD∥平面EFGHABCDFEHG证明 ∵ 四边形EFGH是平行四边形
∴EF∥GH∵GH 平面BCD
EF 平面BCD平面BCD∩平面ACD=CD∴EF∥平面BCD∵EF 平面ACD∴EF∥CD∵EF 平面EFGH CD 平面EFGH∴CD∥平面EFGH线线平行 线面平行判定定理性质定理判断线面平行判断线线平行对比小结 归纳小结: 1.主题:线面平行的性质定理 内容:线面平行则内外直线平行 关键:过已知线找(作)面与已知面相交
