三角形的边角关系(安徽省淮北市烈山区马桥中学王丽丽)
文档属性
| 名称 | 三角形的边角关系(安徽省淮北市烈山区马桥中学王丽丽) |

|
|
| 格式 | rar | ||
| 文件大小 | 704.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-03 00:00:00 | ||
图片预览


文档简介
(共12张PPT)
三角形中的边角关系
授课:马桥中学 王丽丽
创设情境,引入新知
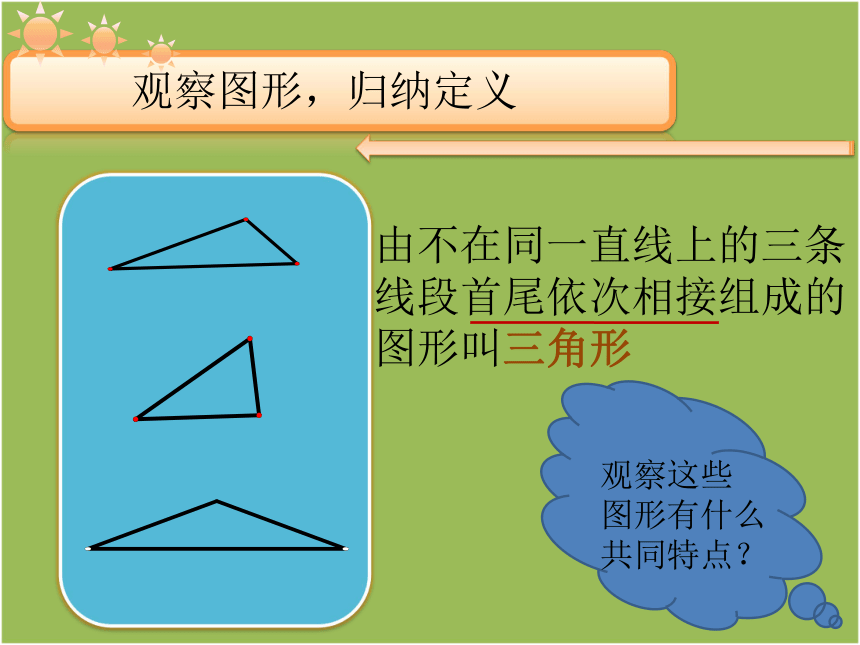
观察图形,归纳定义
观察这些
图形有什么
共同特点?
由不在同一直线上的三条
线段首尾依次相接组成的
图形叫三角形
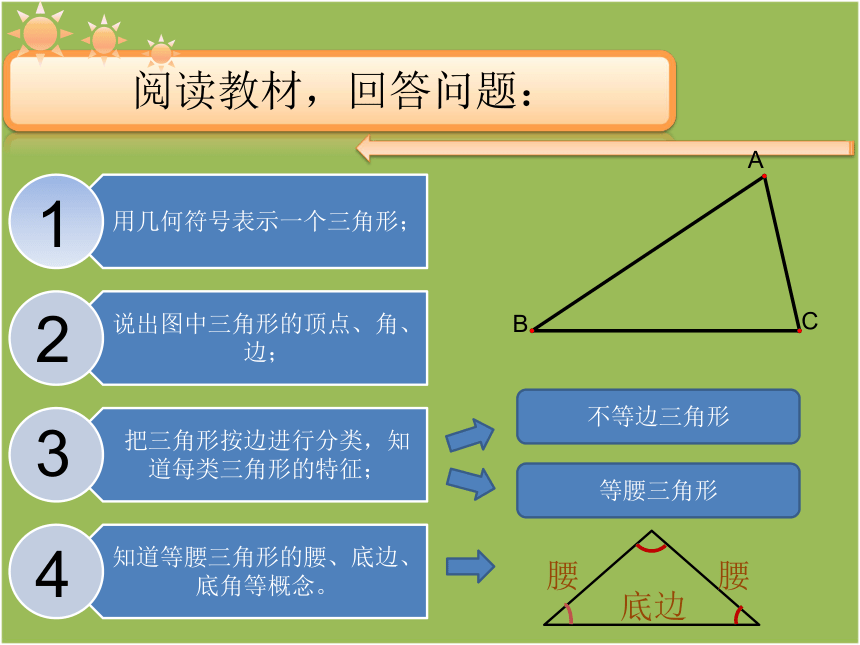
阅读教材,回答问题:
1
2
3
4
A
B
C
不等边三角形
等腰三角形
腰
腰
底边
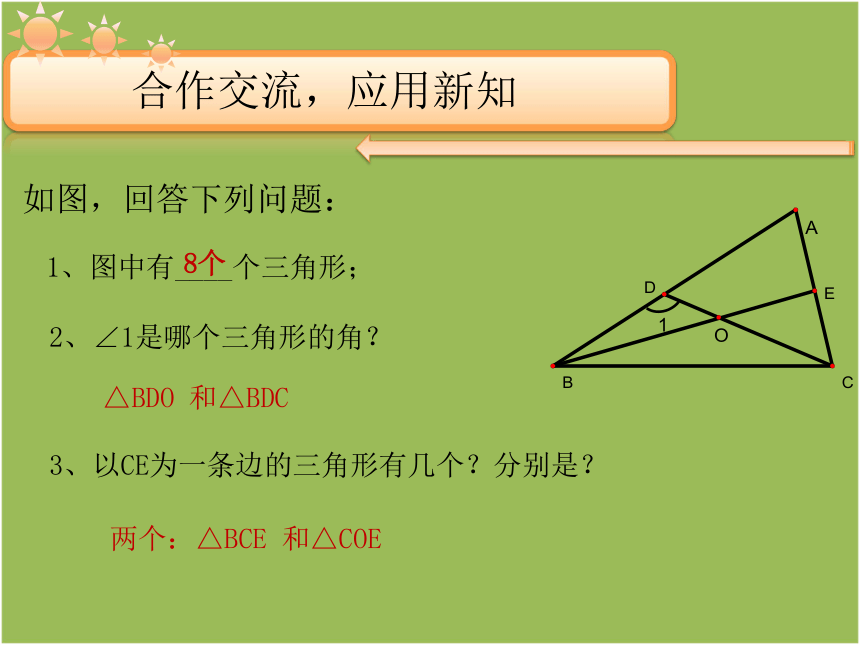
如图,回答下列问题:
1、图中有____个三角形;
2、∠1是哪个三角形的角?
3、以CE为一条边的三角形有几个?分别是?
1
8个
△BDO 和△BDC
两个:△BCE 和△COE
合作交流,应用新知
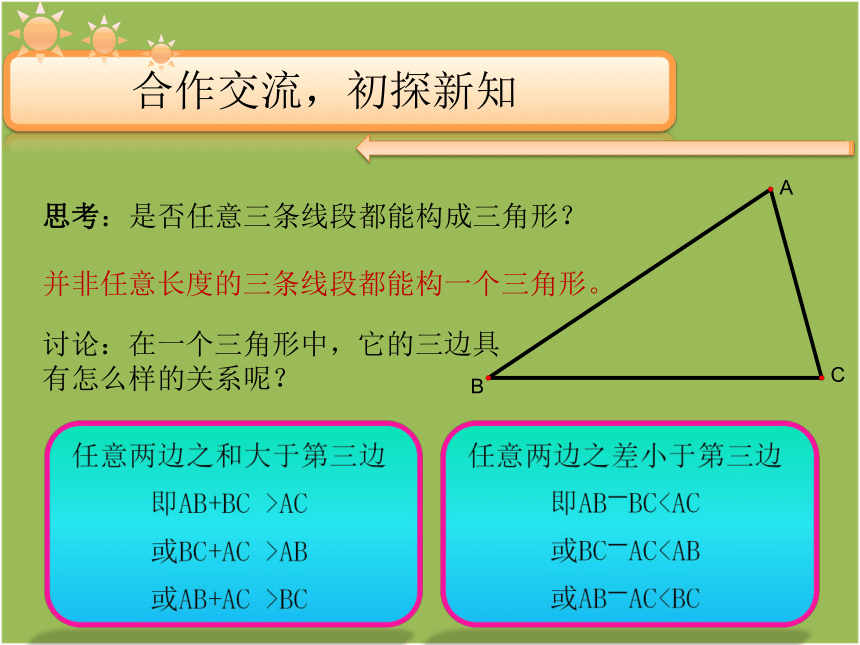
思考:是否任意三条线段都能构成三角形?
并非任意长度的三条线段都能构一个三角形。
讨论:在一个三角形中,它的三边具
有怎么样的关系呢?
合作交流,初探新知
1 、下列长度的三条线段能组成三角形的是( )
(A)1cm 2cm 3cm (B)1cm 3cm 4cm
(C)4cm 5cm 6cm (D)5cm 6cm 13cm;
2 、三角形的三边分别为4cm、6cm、acm
(1)第三边a 的取值范围为______________;
(2)a为偶数时,则a的取值为_________________;
C
2cm4cm或6cm或8cm
强化练习,应用新知
例:等腰三角形中周长为18cm
1、如果腰长是底边长的2倍,求各边的长;
2、如果一边长为4cm,求另两边的长。
(1)设等腰三角形的底边长为xcm,
则腰长为2xcm,根据题意,得
x+2x+2x=18
解方程,得
x=3.6
解:
例题解析,再探新知
(2)若底边长为4cm,设腰长为xcm,则有
2x+4=18
解方程,得
x=7
若一条腰长为4cm,设底边长为xcm,则有
2×4+x=18
x=10
解方程,得
因为4+4<10,所以4cm为一腰不能构成三角形
所以,三角形的另两边长都是7cm
例题解析,再探新知
已知a、b、c是三角形的三条边
化简|a+b-c|+|c-b-a|
应用反思,拓展延伸
解:因为a、b、c是三角形的三边
所以 a+b-c>0(两边之和大于第三边)
c-b-a <0(两边之差小于第三边)
所以|a+b-c|+|c-b-a|=a+b-c-c+b+a
=2a+2b-2c
师生互动,总结新知:
通过本节课的学习,你有哪些收获?
作业设计,深化新知:
三角形中的边角关系
授课:马桥中学 王丽丽
创设情境,引入新知
观察图形,归纳定义
观察这些
图形有什么
共同特点?
由不在同一直线上的三条
线段首尾依次相接组成的
图形叫三角形
阅读教材,回答问题:
1
2
3
4
A
B
C
不等边三角形
等腰三角形
腰
腰
底边
如图,回答下列问题:
1、图中有____个三角形;
2、∠1是哪个三角形的角?
3、以CE为一条边的三角形有几个?分别是?
1
8个
△BDO 和△BDC
两个:△BCE 和△COE
合作交流,应用新知
思考:是否任意三条线段都能构成三角形?
并非任意长度的三条线段都能构一个三角形。
讨论:在一个三角形中,它的三边具
有怎么样的关系呢?
合作交流,初探新知
1 、下列长度的三条线段能组成三角形的是( )
(A)1cm 2cm 3cm (B)1cm 3cm 4cm
(C)4cm 5cm 6cm (D)5cm 6cm 13cm;
2 、三角形的三边分别为4cm、6cm、acm
(1)第三边a 的取值范围为______________;
(2)a为偶数时,则a的取值为_________________;
C
2cm
强化练习,应用新知
例:等腰三角形中周长为18cm
1、如果腰长是底边长的2倍,求各边的长;
2、如果一边长为4cm,求另两边的长。
(1)设等腰三角形的底边长为xcm,
则腰长为2xcm,根据题意,得
x+2x+2x=18
解方程,得
x=3.6
解:
例题解析,再探新知
(2)若底边长为4cm,设腰长为xcm,则有
2x+4=18
解方程,得
x=7
若一条腰长为4cm,设底边长为xcm,则有
2×4+x=18
x=10
解方程,得
因为4+4<10,所以4cm为一腰不能构成三角形
所以,三角形的另两边长都是7cm
例题解析,再探新知
已知a、b、c是三角形的三条边
化简|a+b-c|+|c-b-a|
应用反思,拓展延伸
解:因为a、b、c是三角形的三边
所以 a+b-c>0(两边之和大于第三边)
c-b-a <0(两边之差小于第三边)
所以|a+b-c|+|c-b-a|=a+b-c-c+b+a
=2a+2b-2c
师生互动,总结新知:
通过本节课的学习,你有哪些收获?
作业设计,深化新知:
