2024五四制鲁教版数学八年级下学期--第九章《图形的相似》素养综合检测(含解析)
文档属性
| 名称 | 2024五四制鲁教版数学八年级下学期--第九章《图形的相似》素养综合检测(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 557.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024五四制鲁教版数学八年级下学期
第九章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题4分,共32分)
1.【新独家原创】下列图形中,不是相似图形的一组是
( )
A B C D
2.(2023广东广州天河中学期末)下列各组线段中,成比例的是( )
A.1 cm,2 cm,3 cm,4 cm
B.2 cm,3 cm,4 cm,5 cm
C.1 cm,2 cm,3 cm,5 cm
D.1 cm,2 cm,5 cm,10 cm
3.(2023山东威海经开区期中)若,则的值为( )
A.
4.(2023山东潍坊期中)如图,有甲、乙、丙三个矩形,其中相似的是( )
A.甲与丙 B.甲与乙
C.乙与丙 D.三个矩形都不相似
5.【新考法】(2022河北石家庄一模)如图,某位同学用带有刻度的直尺在数轴上作图,若图中的虚线互相平行,则点P表示的数是( )
A.1 B. D.5
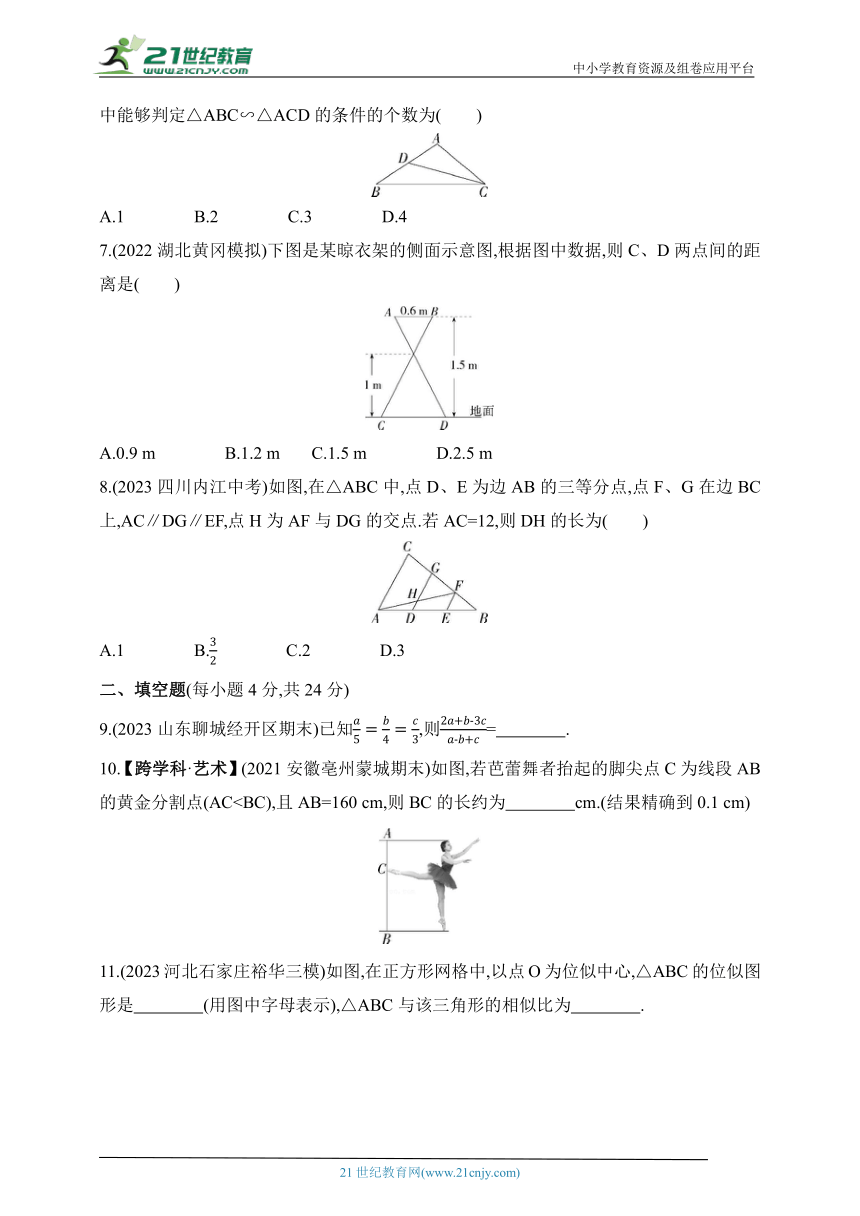
6.如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD·AB.其中能够判定△ABC∽△ACD的条件的个数为( )
A.1 B.2 C.3 D.4
7.(2022湖北黄冈模拟)下图是某晾衣架的侧面示意图,根据图中数据,则C、D两点间的距离是( )
A.0.9 m B.1.2 m C.1.5 m D.2.5 m
8.(2023四川内江中考)如图,在△ABC中,点D、E为边AB的三等分点,点F、G在边BC上,AC∥DG∥EF,点H为AF与DG的交点.若AC=12,则DH的长为( )
A.1 B. C.2 D.3
二、填空题(每小题4分,共24分)
9.(2023山东聊城经开区期末)已知,则= .
10.【跨学科·艺术】(2021安徽亳州蒙城期末)如图,若芭蕾舞者抬起的脚尖点C为线段AB的黄金分割点(AC11.(2023河北石家庄裕华三模)如图,在正方形网格中,以点O为位似中心,△ABC的位似图形是 (用图中字母表示),△ABC与该三角形的相似比为 .
12.(2021山东淄博沂源二模)如图,已知a∥b∥c,且直线a、b、c被直线m、n所截,交点分别为A、B、C和D、E、F,若AB=3,BC=4,
EF=4.8,则DE的长为 .
13.(2022山东淄博周村一模)如图,线段AB、CD的端点都在正方形网格的格点上,它们相交于点M.若每个小正方形的边长都是1,则的值是 .
14.如图,点D在等边三角形ABC的边BC上,连接AD,线段AD的垂直平分线EF分别交边AB,AC于点E,F.当CD=2BD时,的值为 .
三、解答题(共44分)
15.(2022山东济南长清期中)(8分)如图,在平面直角坐标系xOy中,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O为位似中心,在y轴左侧将△OBC的各边放大为原来的两倍,画出放大后的图形△OB'C'.
(2)分别写出B,C两点的对应点B',C'的坐标.
(3)已知M(x,y)为△OBC内的一点,写出M的对应点M'的坐标.
16.(8分)如图,AD为△ABC的边BC上的中线,P为BD上一点,过P作AD的平行线交AB于点Q,交CA的延长线于点R,求证:PQ+PR=2AD.
17.【真实情境】(2023陕西宝鸡陈仓三模)(8分)新明楼,又称新鼓楼,位于榆林城内南大街,如图①.小华查阅资料发现新明楼的高度AB=18.2米,一天他实地观测新明楼,如图②,他在距新明楼30米(FB=30米)的F处,沿FB向点B前进,当走到点H时,小华的眼睛、广告牌CD的顶端C、楼顶A在一条直线上,小华的眼睛到地面的距离为1.7米(EF=GH=1.7米),广告牌的高度CD=3.2米,BD=20米,点B、D、H、F在一条水平线上,AB⊥BF,CD⊥BF,GH⊥BF,EF⊥BF,请求出小华从F处向前走了多少米(即求HF的长).
图① 图②
18.(2021山东烟台海阳期末)(10分)如图,在△ABC中,∠C=90°,AD与BD分别是△ABC的内角∠BAC,∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E,△ABC∽△EDA.
(1)求∠ABC的度数.
(2)求的值.
19.(2023山东泰安岱岳一模)(10分)在△ABC中,D在AC上,且
∠ABD=∠C=45°.
(1)如图1,若AD=4,CD=2,求AB的长度.
(2)如图2,过D作DE⊥AB于E,过点E作EF∥BC交AC于点F,过F作FG⊥BC于G,探究FG与BC的数量关系,并证明你的结论.
图1 图2
答案全解全析
1.D 选项A,B,C中的图形是相似图形;选项D中的图形的形状不相同,不是相似图形.故选D.
2.D A.由于1×4≠2×3,所以不成比例,不符合题意;
B.由于2×5≠3×4,所以不成比例,不符合题意;
C.由于1×5≠2×3,所以不成比例,不符合题意;
D.由于1×10=2×5,所以成比例,符合题意.
故选D.
3.D ∵,故选D.
4.A 三个矩形的角都是直角,矩形甲、乙、丙宽与长的比分别为4∶6=2∶3,1.5∶2=3∶4,2∶3,∴甲和丙相似,故选A.
5.D 本题结合直尺与数轴考查平行线分线段成比例的基本事实的推论.如图,由题意知OB=1.5,OA=3,OC=10,
∵PB∥AC,∴,∴OP=5,
∴点P表示的数是5.故选D.
6.C ∵∠A=∠A,∠B=∠ACD,∴△ABC∽△ACD.
∵∠A=∠A,∠ADC=∠ACB,
∴△ABC∽△ACD.
由∠A=∠A,无法判定△ABC∽△ACD.
∵AC2=AD·AB,∴,
又∵∠A=∠A,
∴△ABC∽△ACD.
∴能够判定△ABC∽△ACD的条件的个数为3.故选C.
7.B 设C、D两点间的距离为x m,AD与BC交于点O(图略),
由题意可知AB∥CD,∴△AOB∽△DOC,
∴,解得x=1.2,
∴C、D两点间的距离是1.2 m.故选B.
8.C ∵点D、E为边AB的三等分点,
∴AD=DE=EB,∴AB=3BE,AE=2AD,
∵EF∥AC,∴△BEF∽△BAC,∴EF∶AC=BE∶AB,
∵AC=12,AB=3BE,∴EF∶12=BE∶3BE,
∴EF=4,
∵DG∥EF,∴△ADH∽△AEF,∴DH∶EF=AD∶AE,
∵EF=4,AE=2AD,∴DH∶4=AD∶2AD,∴DH=2.故选C.
9.答案
解析 设=k,
∴a=5k,b=4k,c=3k,
∴.
10. 答案 98.9
解析 ∵点C为线段AB的黄金分割点(AC∴BC=×160≈98.9 cm.
11. 答案 △GEH;1∶2
解析 根据位似图形的对应点的连线所在直线交于同一点可判断△ABC的位似图形是△GEH,
∵BC∶EH=1∶2,∴相似比为1∶2.
12. 答案 3.6
解析 ∵a∥b∥c,
∴,即,
∴DE=3.6.
13.答案
解析 如图,取格点J,K,连接AJ,JK,KD,BK,BC,设AB与JK的交点为O.
∵AJ∥BK,∴△AJO∽△BKO,
∴JO∶OK=AJ∶BK=1∶3,
∴OK=,
∵DO∥BC,∴△DOM∽△CBM,
∴.
14.答案
解析 如图,连接DE,DF,
∵EF垂直平分AD,∴AE=DE,AF=DF,
在△AEF和△DEF中,
∴△AEF≌△DEF(SSS),∴∠EAF=∠EDF=60°,
∴∠EDB+∠FDC=120°,
∵∠B=60°,∴∠EDB+∠BED=120°,∴∠BED=∠FDC,
∵∠B=∠C=60°,∴△EBD∽△DCF,
∴,
设BD=x,BE=y,则CD=2x,∴CF=,AB=AC=3x,
∴DE=AE=AB-BE=3x-y,DF=AF=AC-CF=3x-,
∴8x2=5xy,∴,
∴.
15.解析 (1)如图,△OB'C'即为所求作的图形.
(2)B'(-6,2),C'(-4,-2).
(3)M'(-2x,-2y).
16.证明 ∵AD∥RP,∴,
∵AD为△ABC的边BC上的中线,∴BD=CD,
∴=2,
∴PQ+PR=2AD.
17.解析 如图,过点G作GM⊥AB于点M,交CD于点N,
则∠AMG=∠CNG=90°,
由题意可得MB=ND=GH=1.7,MN=BD=20,
∴CN=CD-ND=1.5,AM=AB-MB=16.5,
∵∠AGM=∠CGN,∴△AMG∽△CNG,
∴,即,
∴NG=2,∴DH=NG=2,
∴HF=BF-BD-DH=30-20-2=8(米).
∴小华从F处向前走了8米.
18.解析 (1)如图,∵AD与BD分别是△ABC的内角∠BAC,∠ABC的平分线,
∴∠1=∠ABC,∠2=∠BAC,
∵∠C=90°,∴∠1+∠2=(∠ABC+∠BAC)=×(180°-90°)=45°,
∴∠3=∠1+∠2=45°,
∵△ABC∽△EDA,∴∠ABC=∠3=45°.
(2)∵∠3=45°,AE⊥AD,∴∠E=∠3=45°,
∴△ADE是等腰直角三角形,
如图,过A作AF⊥DE于点F,则F为ED的中点.
设AF=a,则DE=2a,DF=a.
在Rt△ADF中,由勾股定理得AD=a.
∵∠ABC=45°,∴∠BAC=45°,
∵2∠1=2∠2=45°,∴∠1=∠2,
∴BD=AD=a+a.
在Rt△ABF中,由勾股定理得AB2=AF2+BF2=a2+()a2.
∵△ABC∽△EDA,
∴.
19.解析 (1)∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,∴,∴AB2=AD·AC,
∵AD=4,CD=2,∴AC=6,∴AB=2.
(2)BC=2FG.证明:如图,连接BF,
∵EF∥BC,∴∠AFE=∠C,
∵∠C=∠ABD,
∴∠AFE=∠ABD,
又∵∠EAF=∠DAB,
∴△AFE∽△ABD.
∴,∴△ABF∽△ADE,
∴∠AED=∠AFB=90°,∴∠BFD=90°,
∵∠C=45°,∴∠FBC=45°=∠C,∴FB=FC,
∵FG⊥BC,∴FG为△ABC的中线,∴BC=2FG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024五四制鲁教版数学八年级下学期
第九章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题4分,共32分)
1.【新独家原创】下列图形中,不是相似图形的一组是
( )
A B C D
2.(2023广东广州天河中学期末)下列各组线段中,成比例的是( )
A.1 cm,2 cm,3 cm,4 cm
B.2 cm,3 cm,4 cm,5 cm
C.1 cm,2 cm,3 cm,5 cm
D.1 cm,2 cm,5 cm,10 cm
3.(2023山东威海经开区期中)若,则的值为( )
A.
4.(2023山东潍坊期中)如图,有甲、乙、丙三个矩形,其中相似的是( )
A.甲与丙 B.甲与乙
C.乙与丙 D.三个矩形都不相似
5.【新考法】(2022河北石家庄一模)如图,某位同学用带有刻度的直尺在数轴上作图,若图中的虚线互相平行,则点P表示的数是( )
A.1 B. D.5
6.如图所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③;④AC2=AD·AB.其中能够判定△ABC∽△ACD的条件的个数为( )
A.1 B.2 C.3 D.4
7.(2022湖北黄冈模拟)下图是某晾衣架的侧面示意图,根据图中数据,则C、D两点间的距离是( )
A.0.9 m B.1.2 m C.1.5 m D.2.5 m
8.(2023四川内江中考)如图,在△ABC中,点D、E为边AB的三等分点,点F、G在边BC上,AC∥DG∥EF,点H为AF与DG的交点.若AC=12,则DH的长为( )
A.1 B. C.2 D.3
二、填空题(每小题4分,共24分)
9.(2023山东聊城经开区期末)已知,则= .
10.【跨学科·艺术】(2021安徽亳州蒙城期末)如图,若芭蕾舞者抬起的脚尖点C为线段AB的黄金分割点(AC
12.(2021山东淄博沂源二模)如图,已知a∥b∥c,且直线a、b、c被直线m、n所截,交点分别为A、B、C和D、E、F,若AB=3,BC=4,
EF=4.8,则DE的长为 .
13.(2022山东淄博周村一模)如图,线段AB、CD的端点都在正方形网格的格点上,它们相交于点M.若每个小正方形的边长都是1,则的值是 .
14.如图,点D在等边三角形ABC的边BC上,连接AD,线段AD的垂直平分线EF分别交边AB,AC于点E,F.当CD=2BD时,的值为 .
三、解答题(共44分)
15.(2022山东济南长清期中)(8分)如图,在平面直角坐标系xOy中,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O为位似中心,在y轴左侧将△OBC的各边放大为原来的两倍,画出放大后的图形△OB'C'.
(2)分别写出B,C两点的对应点B',C'的坐标.
(3)已知M(x,y)为△OBC内的一点,写出M的对应点M'的坐标.
16.(8分)如图,AD为△ABC的边BC上的中线,P为BD上一点,过P作AD的平行线交AB于点Q,交CA的延长线于点R,求证:PQ+PR=2AD.
17.【真实情境】(2023陕西宝鸡陈仓三模)(8分)新明楼,又称新鼓楼,位于榆林城内南大街,如图①.小华查阅资料发现新明楼的高度AB=18.2米,一天他实地观测新明楼,如图②,他在距新明楼30米(FB=30米)的F处,沿FB向点B前进,当走到点H时,小华的眼睛、广告牌CD的顶端C、楼顶A在一条直线上,小华的眼睛到地面的距离为1.7米(EF=GH=1.7米),广告牌的高度CD=3.2米,BD=20米,点B、D、H、F在一条水平线上,AB⊥BF,CD⊥BF,GH⊥BF,EF⊥BF,请求出小华从F处向前走了多少米(即求HF的长).
图① 图②
18.(2021山东烟台海阳期末)(10分)如图,在△ABC中,∠C=90°,AD与BD分别是△ABC的内角∠BAC,∠ABC的平分线,过点A作AE⊥AD,交BD的延长线于点E,△ABC∽△EDA.
(1)求∠ABC的度数.
(2)求的值.
19.(2023山东泰安岱岳一模)(10分)在△ABC中,D在AC上,且
∠ABD=∠C=45°.
(1)如图1,若AD=4,CD=2,求AB的长度.
(2)如图2,过D作DE⊥AB于E,过点E作EF∥BC交AC于点F,过F作FG⊥BC于G,探究FG与BC的数量关系,并证明你的结论.
图1 图2
答案全解全析
1.D 选项A,B,C中的图形是相似图形;选项D中的图形的形状不相同,不是相似图形.故选D.
2.D A.由于1×4≠2×3,所以不成比例,不符合题意;
B.由于2×5≠3×4,所以不成比例,不符合题意;
C.由于1×5≠2×3,所以不成比例,不符合题意;
D.由于1×10=2×5,所以成比例,符合题意.
故选D.
3.D ∵,故选D.
4.A 三个矩形的角都是直角,矩形甲、乙、丙宽与长的比分别为4∶6=2∶3,1.5∶2=3∶4,2∶3,∴甲和丙相似,故选A.
5.D 本题结合直尺与数轴考查平行线分线段成比例的基本事实的推论.如图,由题意知OB=1.5,OA=3,OC=10,
∵PB∥AC,∴,∴OP=5,
∴点P表示的数是5.故选D.
6.C ∵∠A=∠A,∠B=∠ACD,∴△ABC∽△ACD.
∵∠A=∠A,∠ADC=∠ACB,
∴△ABC∽△ACD.
由∠A=∠A,无法判定△ABC∽△ACD.
∵AC2=AD·AB,∴,
又∵∠A=∠A,
∴△ABC∽△ACD.
∴能够判定△ABC∽△ACD的条件的个数为3.故选C.
7.B 设C、D两点间的距离为x m,AD与BC交于点O(图略),
由题意可知AB∥CD,∴△AOB∽△DOC,
∴,解得x=1.2,
∴C、D两点间的距离是1.2 m.故选B.
8.C ∵点D、E为边AB的三等分点,
∴AD=DE=EB,∴AB=3BE,AE=2AD,
∵EF∥AC,∴△BEF∽△BAC,∴EF∶AC=BE∶AB,
∵AC=12,AB=3BE,∴EF∶12=BE∶3BE,
∴EF=4,
∵DG∥EF,∴△ADH∽△AEF,∴DH∶EF=AD∶AE,
∵EF=4,AE=2AD,∴DH∶4=AD∶2AD,∴DH=2.故选C.
9.答案
解析 设=k,
∴a=5k,b=4k,c=3k,
∴.
10. 答案 98.9
解析 ∵点C为线段AB的黄金分割点(AC
11. 答案 △GEH;1∶2
解析 根据位似图形的对应点的连线所在直线交于同一点可判断△ABC的位似图形是△GEH,
∵BC∶EH=1∶2,∴相似比为1∶2.
12. 答案 3.6
解析 ∵a∥b∥c,
∴,即,
∴DE=3.6.
13.答案
解析 如图,取格点J,K,连接AJ,JK,KD,BK,BC,设AB与JK的交点为O.
∵AJ∥BK,∴△AJO∽△BKO,
∴JO∶OK=AJ∶BK=1∶3,
∴OK=,
∵DO∥BC,∴△DOM∽△CBM,
∴.
14.答案
解析 如图,连接DE,DF,
∵EF垂直平分AD,∴AE=DE,AF=DF,
在△AEF和△DEF中,
∴△AEF≌△DEF(SSS),∴∠EAF=∠EDF=60°,
∴∠EDB+∠FDC=120°,
∵∠B=60°,∴∠EDB+∠BED=120°,∴∠BED=∠FDC,
∵∠B=∠C=60°,∴△EBD∽△DCF,
∴,
设BD=x,BE=y,则CD=2x,∴CF=,AB=AC=3x,
∴DE=AE=AB-BE=3x-y,DF=AF=AC-CF=3x-,
∴8x2=5xy,∴,
∴.
15.解析 (1)如图,△OB'C'即为所求作的图形.
(2)B'(-6,2),C'(-4,-2).
(3)M'(-2x,-2y).
16.证明 ∵AD∥RP,∴,
∵AD为△ABC的边BC上的中线,∴BD=CD,
∴=2,
∴PQ+PR=2AD.
17.解析 如图,过点G作GM⊥AB于点M,交CD于点N,
则∠AMG=∠CNG=90°,
由题意可得MB=ND=GH=1.7,MN=BD=20,
∴CN=CD-ND=1.5,AM=AB-MB=16.5,
∵∠AGM=∠CGN,∴△AMG∽△CNG,
∴,即,
∴NG=2,∴DH=NG=2,
∴HF=BF-BD-DH=30-20-2=8(米).
∴小华从F处向前走了8米.
18.解析 (1)如图,∵AD与BD分别是△ABC的内角∠BAC,∠ABC的平分线,
∴∠1=∠ABC,∠2=∠BAC,
∵∠C=90°,∴∠1+∠2=(∠ABC+∠BAC)=×(180°-90°)=45°,
∴∠3=∠1+∠2=45°,
∵△ABC∽△EDA,∴∠ABC=∠3=45°.
(2)∵∠3=45°,AE⊥AD,∴∠E=∠3=45°,
∴△ADE是等腰直角三角形,
如图,过A作AF⊥DE于点F,则F为ED的中点.
设AF=a,则DE=2a,DF=a.
在Rt△ADF中,由勾股定理得AD=a.
∵∠ABC=45°,∴∠BAC=45°,
∵2∠1=2∠2=45°,∴∠1=∠2,
∴BD=AD=a+a.
在Rt△ABF中,由勾股定理得AB2=AF2+BF2=a2+()a2.
∵△ABC∽△EDA,
∴.
19.解析 (1)∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,∴,∴AB2=AD·AC,
∵AD=4,CD=2,∴AC=6,∴AB=2.
(2)BC=2FG.证明:如图,连接BF,
∵EF∥BC,∴∠AFE=∠C,
∵∠C=∠ABD,
∴∠AFE=∠ABD,
又∵∠EAF=∠DAB,
∴△AFE∽△ABD.
∴,∴△ABF∽△ADE,
∴∠AED=∠AFB=90°,∴∠BFD=90°,
∵∠C=45°,∴∠FBC=45°=∠C,∴FB=FC,
∵FG⊥BC,∴FG为△ABC的中线,∴BC=2FG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
