2024五四制鲁教版数学八年级下学期--第六章《特殊平行四边形》素养综合检测(含解析)
文档属性
| 名称 | 2024五四制鲁教版数学八年级下学期--第六章《特殊平行四边形》素养综合检测(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 581.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 08:54:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024五四制鲁教版数学八年级下学期
第六章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题4分,共32分)
1.(2023山东淄博张店期末)菱形、矩形、正方形都具有的性质是( )
A.四条边相等,四个角相等
B.对角线相等
C.对角线互相垂直
D.对角线互相平分
2.(2023安徽合肥三模)如图,a∥b,矩形ABCD的顶点B在直线a上,若∠1=34°,则∠2的度数为( )
A.34° B.46° C.56° D.66°
3.(2023河北石家庄裕华期末)依据所标数据,下列不一定是矩形的为( )
A B
C D
4.【新考向·方案设计题】(2023河北衡水桃城三模)如图,在 ABCD中,AD>AB,∠ABC为锐角,将△ABC沿对角线AC平移,得到△A'B'C',连接AB'、B'D和C'D,若使四边形AB'C'D是菱形,需添加一个条件,现有三种添加方案,甲方案:AB'=DC',乙方案:B'D⊥AC',丙方案:
∠AC'B'=∠AC'D,其中正确的方案是( )
A.甲、乙、丙 B.只有乙、丙 C.只有甲、乙 D.只有甲
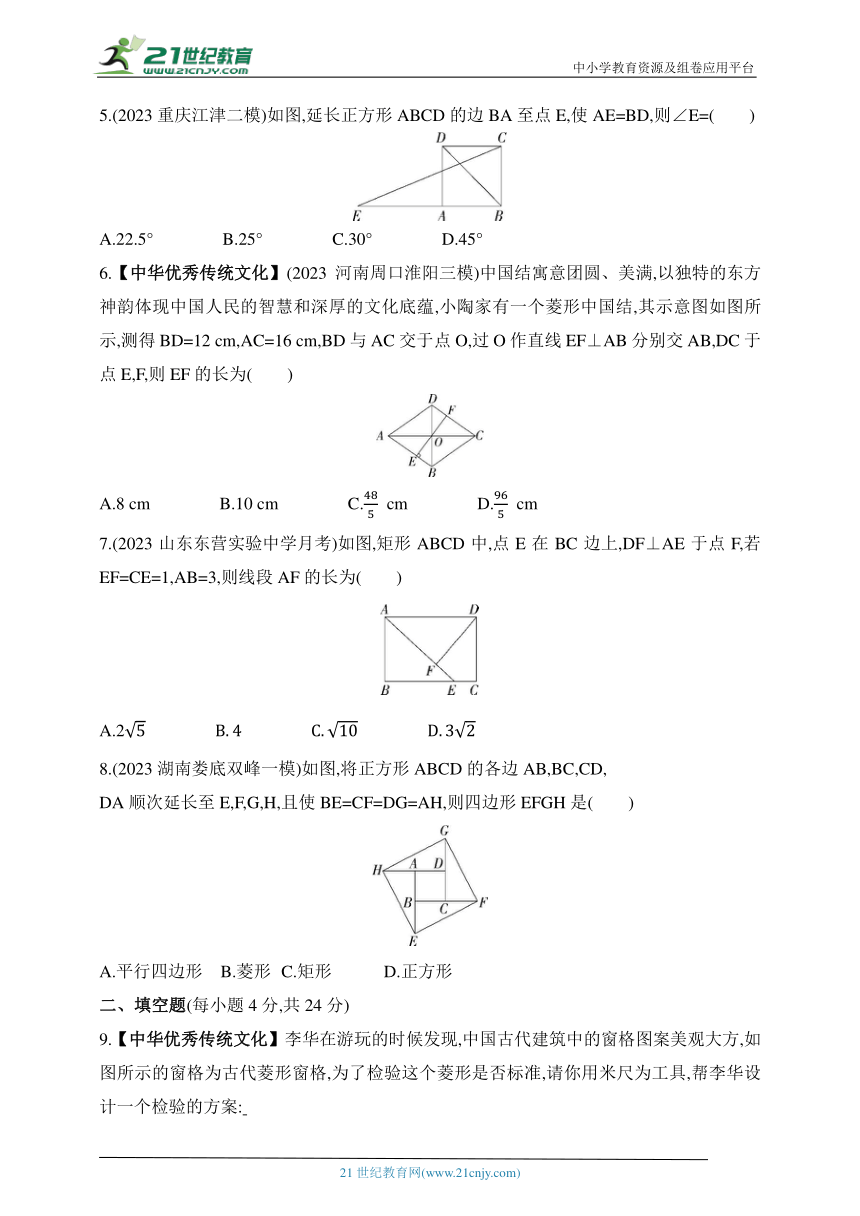
5.(2023重庆江津二模)如图,延长正方形ABCD的边BA至点E,使AE=BD,则∠E=( )
A.22.5° B.25° C.30° D.45°
6.【中华优秀传统文化】(2023河南周口淮阳三模)中国结寓意团圆、美满,以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴,小陶家有一个菱形中国结,其示意图如图所示,测得BD=12 cm,AC=16 cm,BD与AC交于点O,过O作直线EF⊥AB分别交AB,DC于点E,F,则EF的长为( )
A.8 cm B.10 cm C. cm D. cm
7.(2023山东东营实验中学月考)如图,矩形ABCD中,点E在BC边上,DF⊥AE于点F,若EF=CE=1,AB=3,则线段AF的长为( )
A.2
8.(2023湖南娄底双峰一模)如图,将正方形ABCD的各边AB,BC,CD,
DA顺次延长至E,F,G,H,且使BE=CF=DG=AH,则四边形EFGH是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
二、填空题(每小题4分,共24分)
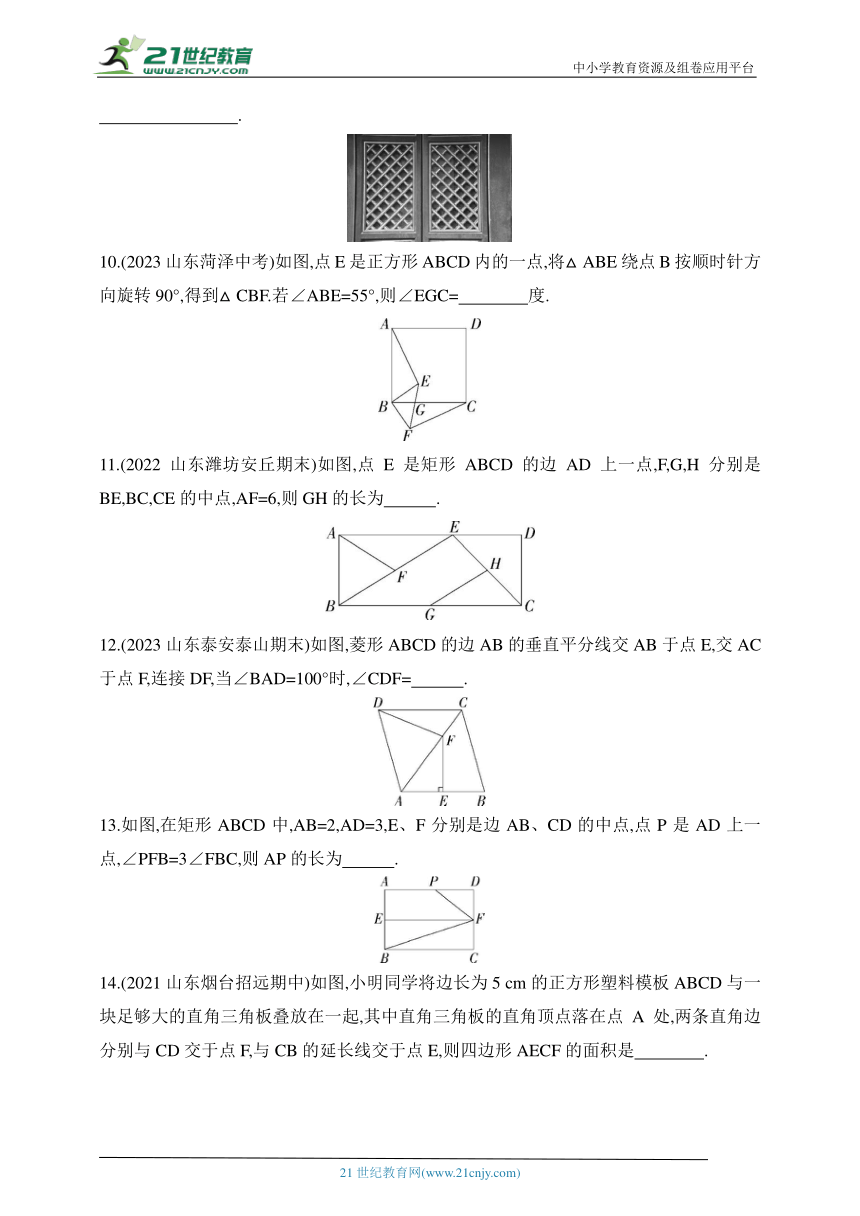
9.【中华优秀传统文化】李华在游玩的时候发现,中国古代建筑中的窗格图案美观大方,如图所示的窗格为古代菱形窗格,为了检验这个菱形是否标准,请你用米尺为工具,帮李华设计一个检验的方案:
.
10.(2023山东菏泽中考)如图,点E是正方形ABCD内的一点,将△ABE绕点B按顺时针方向旋转90°,得到△CBF.若∠ABE=55°,则∠EGC= 度.
11.(2022山东潍坊安丘期末)如图,点E是矩形ABCD的边AD上一点,F,G,H分别是BE,BC,CE的中点,AF=6,则GH的长为 .
12.(2023山东泰安泰山期末)如图,菱形ABCD的边AB的垂直平分线交AB于点E,交AC于点F,连接DF,当∠BAD=100°时,∠CDF= .
13.如图,在矩形ABCD中,AB=2,AD=3,E、F分别是边AB、CD的中点,点P是AD上一点,∠PFB=3∠FBC,则AP的长为 .
14.(2021山东烟台招远期中)如图,小明同学将边长为5 cm的正方形塑料模板ABCD与一块足够大的直角三角板叠放在一起,其中直角三角板的直角顶点落在点A处,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 .
三、解答题(共44分)
15.【新独家原创】(6分)如图,在菱形ABCD中,点M、N分别在AB、CB上,且∠ADM=∠CDN,连接MN,BD,求证:BD垂直平分MN.
16.(2021山东泰安新泰期中)(8分)如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E为AC的中点,EF⊥BD,垂足为F.
(1)求证:BE=DE.
(2)若AC=26,EF=5,求BD的长.
17.(2023江西宜春高安期中)(8分)如图,在矩形ABCD中,对角线AC和BD相交于O点,AE平分∠BAD交BC于点E,且∠CAE=15°,连接OE.
(1)求证:△AOB为等边三角形.
(2)求∠COE的度数.
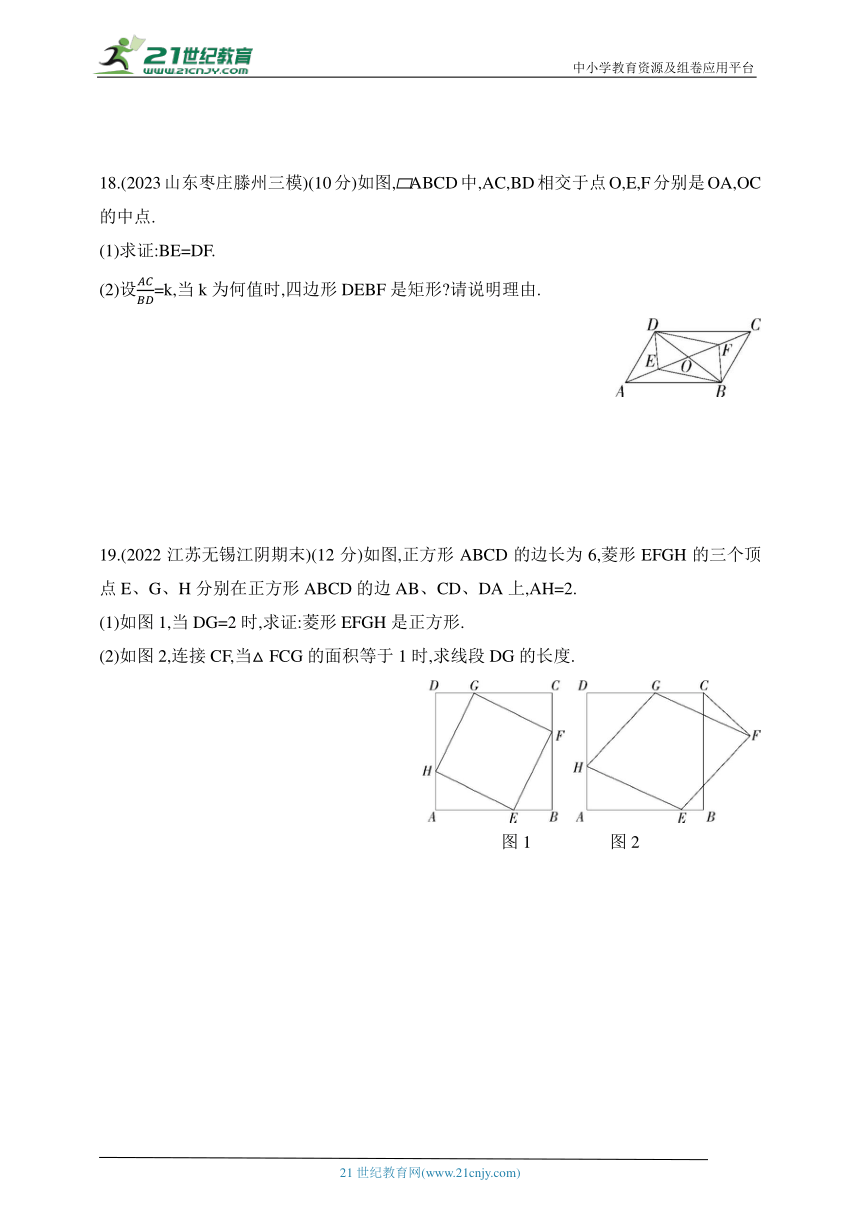
18.(2023山东枣庄滕州三模)(10分)如图, ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
(1)求证:BE=DF.
(2)设=k,当k为何值时,四边形DEBF是矩形 请说明理由.
19.(2022江苏无锡江阴期末)(12分)如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,AH=2.
(1)如图1,当DG=2时,求证:菱形EFGH是正方形.
(2)如图2,连接CF,当△FCG的面积等于1时,求线段DG的长度.
图1 图2
答案全解全析
1.D 根据菱形、矩形、正方形的性质可知D正确.
2.C 过点A作AE∥a,如图,
∴∠EAB=∠1=34°.
∵a∥b,AE∥a,∴AE∥b,
∴∠2=∠DAE,
∵四边形ABCD为矩形,
∴∠DAB=90°,
∴∠2=∠DAE=90°-∠EAB=56°.
故选C.
3.B A.对边平行且相等的四边形是平行四边形,有一个角是直角的平行四边形是矩形,故该选项不符合题意;B.不能证明该图形是矩形,故该选项符合题意;C.有三个角是直角的四边形是矩形,故该选项不符合题意;D.有两组对边分别相等的四边形是平行四边形,有一个角是直角的平行四边形是矩形,故该选项不符合题意.故选B.
4.B 根据题意可知AD=B'C',AD∥B'C',
∴四边形AB'C'D是平行四边形,
甲方案:添加AB'=DC'不能判定平行四边形AB'C'D是菱形;
乙方案:∵B'D⊥AC',∴平行四边形AB'C'D是菱形;
丙方案:∵AD∥B'C',∴∠DAC'=∠AC'B',
∵∠AC'B'=∠AC'D,
∴∠DAC'=∠AC'D,∴AD=C'D,
∴平行四边形AB'C'D是菱形.
∴正确的方案是乙和丙.
故选B.
5.A 连接AC,如图,
∵四边形ABCD是正方形,∴AC=BD,且∠CAB=45°,
又∵BD=AE,∴AE=CA,∴∠E=∠ACE,
∵∠CAB=∠ACE+∠E=2∠E=45°,
∴∠E=22.5°.故选A.
6.C ∵四边形ABCD是菱形,
∴AC⊥BD,AO=AC=8 cm,BO=BD=6 cm,
∴AB==10 cm,
∵S菱形ABCD=AC·BD=AB·EF,
∴ cm.故选C.
7.B 如图,连接DE,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠BCD=90°,
∴∠ADE=∠DEC,
∵DF⊥AE,∴∠DFE=90°,
∵DE=DE,FE=CE,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC,∠FED=∠DEC,
∴∠FED=∠ADE,∴AE=AD,∴AE=BC,
在Rt△ABE中,设AE=x,则BC=x,BE=x-1,
由勾股定理可得AB2+BE2=AE2,即32+(x-1)2=x2,
解得x=5,即AE=5,
∴AF=AE-EF=5-1=4.
故选B.
8.D ∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°,
∴∠FBE=∠GCF=∠HDG=∠EAH=90°,
∵BE=CF=DG=AH,
∴AB+BE=BC+CF=CD+DG=DA+AH,
即AE=BF=CG=DH,
在△FBE和△GCF中,
∴△FBE≌△GCF(SAS),
∴EF=FG,∠BFE=∠CGF,
∵∠GCF=90°,∴∠CGF+∠GFC=90°,
∴∠BFE+∠GFC=90°,即∠EFG=90°,
易证得△GCF≌△HDG≌△EAH≌△FBE,
∴FG=GH=HE=EF,
∴四边形EFGH是菱形,
又∵∠EFG=90°,∴四边形EFGH是正方形.
故选D.
9. 答案 用米尺测量窗格中菱形的四条边的长度是否相等,如果四条边的长度相等,那么这个菱形就是标准的
解析 四条边都相等的四边形是菱形.
10. 答案 80
解析 ∵四边形ABCD是正方形,∴∠ABC=90°,
∵∠ABE=55°,∴∠EBC=∠ABC-∠ABE=35°,
由旋转得BE=BF,∠EBF=90°,∴∠BEF=∠BFE=45°,
∵∠EGC是△BEG的一个外角,
∴∠EGC=∠BEG+∠EBG=80°.
11. 答案 6
解析 在矩形ABCD中,∠BAD=90°,
∵F为BE的中点,AF=6,∴BE=2AF=12.
∵G,H分别为BC,EC的中点,∴GH=BE=6.
12. 答案 30°
解析 如图,连接BF,
∵四边形ABCD是菱形,
∴CD=BC,∠DCF=∠BCF,∠DAC=∠BAC.
∵∠BAD=100°,∴∠BAF=∠BAD=50°,
在△DCF和△BCF中,
∴△DCF≌△BCF(SAS),
∴∠CBF=∠CDF.
∵FE垂直平分AB,
∴AF=BF,∴∠ABF=∠BAF=50°,
∵∠ABC=180°-∠BAD=80°,
∴∠CBF=∠ABC-∠ABF=80°-50°=30°,
∴∠CDF=30°.
13.答案
解析 如图,连接AF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,AD∥BC,AB∥CD,
∵E、F分别是边AB、CD的中点,
∴AE=EB,DF=FC,∴AE=DF,BE=CF,
∴四边形AEFD、四边形BCFE是平行四边形,
∵∠D=∠C=90°,
∴四边形AEFD、四边形BCFE都是矩形,
∴EF∥AD∥BC,∠AEF=90°,∴EF⊥AB,
∵AE=EB,∴FA=FB,∠AFE=∠EFB,
∵EF∥BC∥AD,∴∠EFB=∠FBC,∠DAF=∠AFE,
∵∠PFB=3∠FBC,∴∠PFA=∠AFE=∠EFB,
∴∠PFA=∠PAF,∴PA=PF,
设PA=PF=x,则PD=3-x,在Rt△PDF中,由勾股定理得PF2=PD2+DF2,即x2=(3-x)2+12,
解得x=,即AP的长为.
14. 答案 25 cm2
解析 ∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠D=90°,AB=AD.
∴∠DAF+∠BAF=90°,
∵∠EAF=90°,
∴∠EAB+∠BAF=90°.
∴∠EAB=∠DAF,
在△EAB和△FAD中,
∴△EAB≌△FAD(ASA),
∴S△EAB=S△FAD,
∵S四边形AECF=S四边形ABCF+S△ABE,
∴S四边形AECF=S四边形ABCF+S△ADF=S正方形ABCD=52=25(cm2).
15.证明 ∵四边形ABCD为菱形,
∴AD=CD=AB=BC,∠A=∠C,∠ABD=∠CBD.
在△AMD和△CND中,
∴△AMD≌△CND(ASA),
∴AM=CN,
∵AB=BC,∴AB-AM=BC-CN,即BM=BN.
又∵∠ABD=∠CBD,∴BD垂直平分MN.
16.解析 (1)证明:∵∠ABC=∠ADC=90°,点E为AC的中点,
∴BE=AC,∴BE=DE.
(2)∵BE=DE,EF⊥BD,∴BD=2BF,
∵BE=AC,AC=26,∴BE=13,
∵EF=5,∴BF==12,
∴BD=2BF=24.
17.解析 (1)证明:∵四边形ABCD是矩形,
∴OA=OC=OB=OD,∠BAD=90°,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∵∠CAE=15°,∴∠BAC=45°+15°=60°,
∴△BAO是等边三角形.
(2)∵△AOB是等边三角形,
∴AB=OB,∠ABO=∠AOB=60°,
∴∠OBC=90°-60°=30°,
∵∠BAE=45°,∠ABC=90°,∴∠AEB=45°=∠BAE,
∴AB=BE,∴OB=BE,
∴∠BOE=∠BEO=×(180°-30°)=75°,
∴∠COE=180°-∠BOE-∠AOB=180°-75°-60°=45°.
18.解析 (1)证明:∵四边形ABCD为平行四边形,
∴BO=OD,AO=OC,
∵E,F分别为AO,OC的中点,
∴EO=OC,∴EO=FO,
∵BO=OD,
∴四边形DEBF是平行四边形,∴BE=DF.
(2)当k=2时,四边形DEBF是矩形.
理由:∵AC,
∵E,F分别为OA,OC的中点,
∴EF=OE+OF=AC=BD,
∴平行四边形DEBF为矩形,
即当k=2时,四边形DEBF是矩形.
19.解析 (1)证明:∵四边形ABCD是正方形,
∴∠D=∠A=90°,∴∠AEH+∠AHE=90°.
∵四边形EFGH是菱形,∴HG=HE,
在Rt△HDG和Rt△EAH中,
∴Rt△HDG≌Rt△EAH(HL),
∴∠DHG=∠AEH,∴∠DHG+∠AHE=90°,
∴∠GHE=90°,∴菱形EFGH为正方形.
(2)如图,过F作FM⊥DC,交DC的延长线于点M,连接GE,
即∠M=∠A=90°,
∵CD∥AB,∴∠AEG=∠MGE,
在菱形EFGH中,HE=FG,HE∥FG,
∴∠HEG=∠FGE,∴∠AEH=∠FGM.
在△EHA和△GFM中,
∴△EHA≌△GFM(AAS),
∴MF=AH=2,
设DG=x,则CG=6-x,
∵S△FCG=CG·FM=6-x=1,∴x=5,即DG=5,
故线段DG的长度为5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024五四制鲁教版数学八年级下学期
第六章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题4分,共32分)
1.(2023山东淄博张店期末)菱形、矩形、正方形都具有的性质是( )
A.四条边相等,四个角相等
B.对角线相等
C.对角线互相垂直
D.对角线互相平分
2.(2023安徽合肥三模)如图,a∥b,矩形ABCD的顶点B在直线a上,若∠1=34°,则∠2的度数为( )
A.34° B.46° C.56° D.66°
3.(2023河北石家庄裕华期末)依据所标数据,下列不一定是矩形的为( )
A B
C D
4.【新考向·方案设计题】(2023河北衡水桃城三模)如图,在 ABCD中,AD>AB,∠ABC为锐角,将△ABC沿对角线AC平移,得到△A'B'C',连接AB'、B'D和C'D,若使四边形AB'C'D是菱形,需添加一个条件,现有三种添加方案,甲方案:AB'=DC',乙方案:B'D⊥AC',丙方案:
∠AC'B'=∠AC'D,其中正确的方案是( )
A.甲、乙、丙 B.只有乙、丙 C.只有甲、乙 D.只有甲
5.(2023重庆江津二模)如图,延长正方形ABCD的边BA至点E,使AE=BD,则∠E=( )
A.22.5° B.25° C.30° D.45°
6.【中华优秀传统文化】(2023河南周口淮阳三模)中国结寓意团圆、美满,以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴,小陶家有一个菱形中国结,其示意图如图所示,测得BD=12 cm,AC=16 cm,BD与AC交于点O,过O作直线EF⊥AB分别交AB,DC于点E,F,则EF的长为( )
A.8 cm B.10 cm C. cm D. cm
7.(2023山东东营实验中学月考)如图,矩形ABCD中,点E在BC边上,DF⊥AE于点F,若EF=CE=1,AB=3,则线段AF的长为( )
A.2
8.(2023湖南娄底双峰一模)如图,将正方形ABCD的各边AB,BC,CD,
DA顺次延长至E,F,G,H,且使BE=CF=DG=AH,则四边形EFGH是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
二、填空题(每小题4分,共24分)
9.【中华优秀传统文化】李华在游玩的时候发现,中国古代建筑中的窗格图案美观大方,如图所示的窗格为古代菱形窗格,为了检验这个菱形是否标准,请你用米尺为工具,帮李华设计一个检验的方案:
.
10.(2023山东菏泽中考)如图,点E是正方形ABCD内的一点,将△ABE绕点B按顺时针方向旋转90°,得到△CBF.若∠ABE=55°,则∠EGC= 度.
11.(2022山东潍坊安丘期末)如图,点E是矩形ABCD的边AD上一点,F,G,H分别是BE,BC,CE的中点,AF=6,则GH的长为 .
12.(2023山东泰安泰山期末)如图,菱形ABCD的边AB的垂直平分线交AB于点E,交AC于点F,连接DF,当∠BAD=100°时,∠CDF= .
13.如图,在矩形ABCD中,AB=2,AD=3,E、F分别是边AB、CD的中点,点P是AD上一点,∠PFB=3∠FBC,则AP的长为 .
14.(2021山东烟台招远期中)如图,小明同学将边长为5 cm的正方形塑料模板ABCD与一块足够大的直角三角板叠放在一起,其中直角三角板的直角顶点落在点A处,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 .
三、解答题(共44分)
15.【新独家原创】(6分)如图,在菱形ABCD中,点M、N分别在AB、CB上,且∠ADM=∠CDN,连接MN,BD,求证:BD垂直平分MN.
16.(2021山东泰安新泰期中)(8分)如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E为AC的中点,EF⊥BD,垂足为F.
(1)求证:BE=DE.
(2)若AC=26,EF=5,求BD的长.
17.(2023江西宜春高安期中)(8分)如图,在矩形ABCD中,对角线AC和BD相交于O点,AE平分∠BAD交BC于点E,且∠CAE=15°,连接OE.
(1)求证:△AOB为等边三角形.
(2)求∠COE的度数.
18.(2023山东枣庄滕州三模)(10分)如图, ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
(1)求证:BE=DF.
(2)设=k,当k为何值时,四边形DEBF是矩形 请说明理由.
19.(2022江苏无锡江阴期末)(12分)如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,AH=2.
(1)如图1,当DG=2时,求证:菱形EFGH是正方形.
(2)如图2,连接CF,当△FCG的面积等于1时,求线段DG的长度.
图1 图2
答案全解全析
1.D 根据菱形、矩形、正方形的性质可知D正确.
2.C 过点A作AE∥a,如图,
∴∠EAB=∠1=34°.
∵a∥b,AE∥a,∴AE∥b,
∴∠2=∠DAE,
∵四边形ABCD为矩形,
∴∠DAB=90°,
∴∠2=∠DAE=90°-∠EAB=56°.
故选C.
3.B A.对边平行且相等的四边形是平行四边形,有一个角是直角的平行四边形是矩形,故该选项不符合题意;B.不能证明该图形是矩形,故该选项符合题意;C.有三个角是直角的四边形是矩形,故该选项不符合题意;D.有两组对边分别相等的四边形是平行四边形,有一个角是直角的平行四边形是矩形,故该选项不符合题意.故选B.
4.B 根据题意可知AD=B'C',AD∥B'C',
∴四边形AB'C'D是平行四边形,
甲方案:添加AB'=DC'不能判定平行四边形AB'C'D是菱形;
乙方案:∵B'D⊥AC',∴平行四边形AB'C'D是菱形;
丙方案:∵AD∥B'C',∴∠DAC'=∠AC'B',
∵∠AC'B'=∠AC'D,
∴∠DAC'=∠AC'D,∴AD=C'D,
∴平行四边形AB'C'D是菱形.
∴正确的方案是乙和丙.
故选B.
5.A 连接AC,如图,
∵四边形ABCD是正方形,∴AC=BD,且∠CAB=45°,
又∵BD=AE,∴AE=CA,∴∠E=∠ACE,
∵∠CAB=∠ACE+∠E=2∠E=45°,
∴∠E=22.5°.故选A.
6.C ∵四边形ABCD是菱形,
∴AC⊥BD,AO=AC=8 cm,BO=BD=6 cm,
∴AB==10 cm,
∵S菱形ABCD=AC·BD=AB·EF,
∴ cm.故选C.
7.B 如图,连接DE,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠BCD=90°,
∴∠ADE=∠DEC,
∵DF⊥AE,∴∠DFE=90°,
∵DE=DE,FE=CE,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC,∠FED=∠DEC,
∴∠FED=∠ADE,∴AE=AD,∴AE=BC,
在Rt△ABE中,设AE=x,则BC=x,BE=x-1,
由勾股定理可得AB2+BE2=AE2,即32+(x-1)2=x2,
解得x=5,即AE=5,
∴AF=AE-EF=5-1=4.
故选B.
8.D ∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°,
∴∠FBE=∠GCF=∠HDG=∠EAH=90°,
∵BE=CF=DG=AH,
∴AB+BE=BC+CF=CD+DG=DA+AH,
即AE=BF=CG=DH,
在△FBE和△GCF中,
∴△FBE≌△GCF(SAS),
∴EF=FG,∠BFE=∠CGF,
∵∠GCF=90°,∴∠CGF+∠GFC=90°,
∴∠BFE+∠GFC=90°,即∠EFG=90°,
易证得△GCF≌△HDG≌△EAH≌△FBE,
∴FG=GH=HE=EF,
∴四边形EFGH是菱形,
又∵∠EFG=90°,∴四边形EFGH是正方形.
故选D.
9. 答案 用米尺测量窗格中菱形的四条边的长度是否相等,如果四条边的长度相等,那么这个菱形就是标准的
解析 四条边都相等的四边形是菱形.
10. 答案 80
解析 ∵四边形ABCD是正方形,∴∠ABC=90°,
∵∠ABE=55°,∴∠EBC=∠ABC-∠ABE=35°,
由旋转得BE=BF,∠EBF=90°,∴∠BEF=∠BFE=45°,
∵∠EGC是△BEG的一个外角,
∴∠EGC=∠BEG+∠EBG=80°.
11. 答案 6
解析 在矩形ABCD中,∠BAD=90°,
∵F为BE的中点,AF=6,∴BE=2AF=12.
∵G,H分别为BC,EC的中点,∴GH=BE=6.
12. 答案 30°
解析 如图,连接BF,
∵四边形ABCD是菱形,
∴CD=BC,∠DCF=∠BCF,∠DAC=∠BAC.
∵∠BAD=100°,∴∠BAF=∠BAD=50°,
在△DCF和△BCF中,
∴△DCF≌△BCF(SAS),
∴∠CBF=∠CDF.
∵FE垂直平分AB,
∴AF=BF,∴∠ABF=∠BAF=50°,
∵∠ABC=180°-∠BAD=80°,
∴∠CBF=∠ABC-∠ABF=80°-50°=30°,
∴∠CDF=30°.
13.答案
解析 如图,连接AF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,AD∥BC,AB∥CD,
∵E、F分别是边AB、CD的中点,
∴AE=EB,DF=FC,∴AE=DF,BE=CF,
∴四边形AEFD、四边形BCFE是平行四边形,
∵∠D=∠C=90°,
∴四边形AEFD、四边形BCFE都是矩形,
∴EF∥AD∥BC,∠AEF=90°,∴EF⊥AB,
∵AE=EB,∴FA=FB,∠AFE=∠EFB,
∵EF∥BC∥AD,∴∠EFB=∠FBC,∠DAF=∠AFE,
∵∠PFB=3∠FBC,∴∠PFA=∠AFE=∠EFB,
∴∠PFA=∠PAF,∴PA=PF,
设PA=PF=x,则PD=3-x,在Rt△PDF中,由勾股定理得PF2=PD2+DF2,即x2=(3-x)2+12,
解得x=,即AP的长为.
14. 答案 25 cm2
解析 ∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠D=90°,AB=AD.
∴∠DAF+∠BAF=90°,
∵∠EAF=90°,
∴∠EAB+∠BAF=90°.
∴∠EAB=∠DAF,
在△EAB和△FAD中,
∴△EAB≌△FAD(ASA),
∴S△EAB=S△FAD,
∵S四边形AECF=S四边形ABCF+S△ABE,
∴S四边形AECF=S四边形ABCF+S△ADF=S正方形ABCD=52=25(cm2).
15.证明 ∵四边形ABCD为菱形,
∴AD=CD=AB=BC,∠A=∠C,∠ABD=∠CBD.
在△AMD和△CND中,
∴△AMD≌△CND(ASA),
∴AM=CN,
∵AB=BC,∴AB-AM=BC-CN,即BM=BN.
又∵∠ABD=∠CBD,∴BD垂直平分MN.
16.解析 (1)证明:∵∠ABC=∠ADC=90°,点E为AC的中点,
∴BE=AC,∴BE=DE.
(2)∵BE=DE,EF⊥BD,∴BD=2BF,
∵BE=AC,AC=26,∴BE=13,
∵EF=5,∴BF==12,
∴BD=2BF=24.
17.解析 (1)证明:∵四边形ABCD是矩形,
∴OA=OC=OB=OD,∠BAD=90°,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∵∠CAE=15°,∴∠BAC=45°+15°=60°,
∴△BAO是等边三角形.
(2)∵△AOB是等边三角形,
∴AB=OB,∠ABO=∠AOB=60°,
∴∠OBC=90°-60°=30°,
∵∠BAE=45°,∠ABC=90°,∴∠AEB=45°=∠BAE,
∴AB=BE,∴OB=BE,
∴∠BOE=∠BEO=×(180°-30°)=75°,
∴∠COE=180°-∠BOE-∠AOB=180°-75°-60°=45°.
18.解析 (1)证明:∵四边形ABCD为平行四边形,
∴BO=OD,AO=OC,
∵E,F分别为AO,OC的中点,
∴EO=OC,∴EO=FO,
∵BO=OD,
∴四边形DEBF是平行四边形,∴BE=DF.
(2)当k=2时,四边形DEBF是矩形.
理由:∵AC,
∵E,F分别为OA,OC的中点,
∴EF=OE+OF=AC=BD,
∴平行四边形DEBF为矩形,
即当k=2时,四边形DEBF是矩形.
19.解析 (1)证明:∵四边形ABCD是正方形,
∴∠D=∠A=90°,∴∠AEH+∠AHE=90°.
∵四边形EFGH是菱形,∴HG=HE,
在Rt△HDG和Rt△EAH中,
∴Rt△HDG≌Rt△EAH(HL),
∴∠DHG=∠AEH,∴∠DHG+∠AHE=90°,
∴∠GHE=90°,∴菱形EFGH为正方形.
(2)如图,过F作FM⊥DC,交DC的延长线于点M,连接GE,
即∠M=∠A=90°,
∵CD∥AB,∴∠AEG=∠MGE,
在菱形EFGH中,HE=FG,HE∥FG,
∴∠HEG=∠FGE,∴∠AEH=∠FGM.
在△EHA和△GFM中,
∴△EHA≌△GFM(AAS),
∴MF=AH=2,
设DG=x,则CG=6-x,
∵S△FCG=CG·FM=6-x=1,∴x=5,即DG=5,
故线段DG的长度为5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
