2024五四制鲁教版数学八年级下学期--期末素养综合测试(一)(含解析)
文档属性
| 名称 | 2024五四制鲁教版数学八年级下学期--期末素养综合测试(一)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 531.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024五四制鲁教版数学八年级下学期
期末素养综合测试(一)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.(2023山东济宁高新区期中)下列是一元二次方程的是(( )
A.2x-3y+1 B.3x+y=z
C.x2-5x=1 D.x2-+2=0
2.(2023山东威海环翠期中)下列各式是最简二次根式的是( )
A.
3.(2023山东济南莱芜陈毅中学期中)已知2x=3y(y≠0),则下面结论成立的是( )
A.
C.
4.如图,以点O为位似中心,把△ABC各边扩大为原来的2倍得到△A'B'C'.以下说法中错误的是( )
A.△ABC∽△A'B'C'
B.C,O,C'三点在同一条直线上
C.AO∶AA'=1∶2
D.AB∥A'B'
5.(2022山东聊城东昌府一模)下列计算正确的是 ( )
A.
C.
6.【新独家原创】如图,将三个全等的矩形拼成一个大矩形ABCD,连接BD,与EF,GH分别交于M,N两点.若AB=9,BF=4,则线段MN的长为( )
A.3 B.4
C.5 D.6
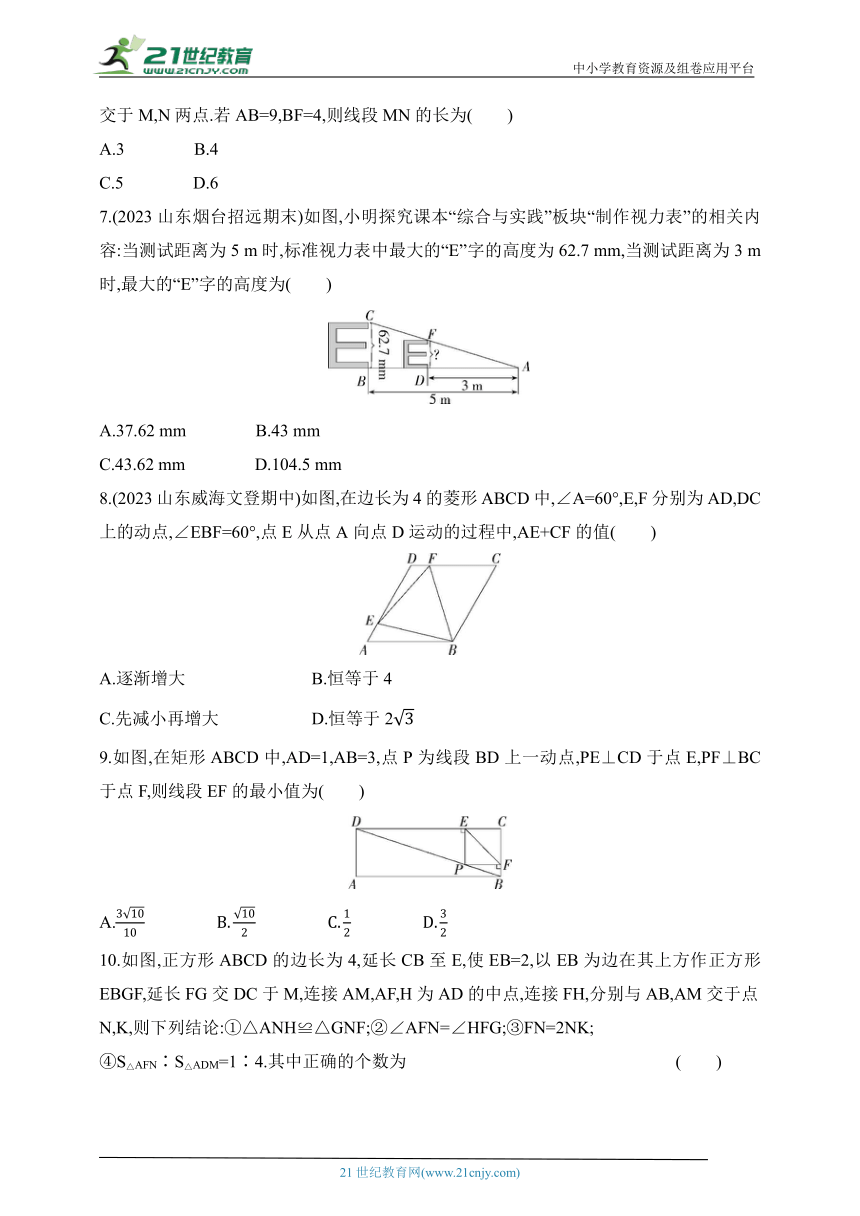
7.(2023山东烟台招远期末)如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5 m时,标准视力表中最大的“E”字的高度为62.7 mm,当测试距离为3 m时,最大的“E”字的高度为( )
A.37.62 mm B.43 mm
C.43.62 mm D.104.5 mm
8.(2023山东威海文登期中)如图,在边长为4的菱形ABCD中,∠A=60°,E,F分别为AD,DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的值( )
A.逐渐增大 B.恒等于4
C.先减小再增大 D.恒等于2
9.如图,在矩形ABCD中,AD=1,AB=3,点P为线段BD上一动点,PE⊥CD于点E,PF⊥BC于点F,则线段EF的最小值为( )
A.
10.如图,正方形ABCD的边长为4,延长CB至E,使EB=2,以EB为边在其上方作正方形EBGF,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH,分别与AB,AM交于点N,K,则下列结论:①△ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;
④S△AFN∶S△ADM=1∶4.其中正确的个数为 ( )
A.1 B.2
C.3 D.4
二、填空题(每小题4分,共24分)
11.(2023山东泰安十五中月考)二次根式有意义,那么x的取值范围是 .
12.(2023山东聊城临清期末)已知实数a在数轴上对应的点的位置如图所示,则化简的结果是 .
13.(2021辽宁沈阳模拟)如图,在△ABC中,点D在BC边上,AB=AD,点E,F分别是AC,BD的中点,EF=2.5,则AC的长为 .
14.(2023山东济南莱芜胜利中学期中)如图,菱形ABCD的边长为3,过点A、C作对角线AC的垂线,分别交CB和AD的延长线于点E、F,AE=4,则四边形AECF的周长为 .
15.(2021山东淄博桓台期末)在△ABC中,∠B=36°,AB=AC,D是BC上一点,满足AD=CD,则= .
16.如图,小明用相似图形的知识测量旗杆高度,已知小明的眼睛离地面1.5米(AB=1.5米),他将3米长的标杆CD竖直放置在身前3米处(AC=3米),此时小明的眼睛、标杆的顶端、旗杆的顶端在一条直线上,通过计算得旗杆的高度为15米(EF=15米),则旗杆和标杆之间的水平距离CE为 米.
三、解答题(共66分)
17.[含评分细则](6分)
(1)(2023山东济宁任城期中)计算:(.
(2)解方程:x(2x-1)=4x-2.
18.[含评分细则](2023山东烟台莱州期中)(6分)已知∠ACB=90°,
BC=2,CD是AB边上的高,求CD的长.
19.[含评分细则](2021辽宁抚顺新抚一模)(8分)如图,△ABC的三个顶点的坐标分别为A(3,1),B(1,2),C(4,3).
(1)以原点O为位似中心,在第一象限内将△ABC的各边放大为原来的2倍得到△A1B1C1,作出△A1B1C1,写出A1,B1,C1的坐标.
(2)若P为第一象限内的整点(横、纵坐标都是整数的点),AP平分∠BAC,直接写出点P的坐标.
20.[含评分细则](2023山东青岛莱西期中)(8分)某商场促销一种商品,促销方式如下:
1.售价为150元/个; 2.若购买数量超过10个,则单价按每增加2个减5元的方式计算; 3.一次性购买不得超过30个.
小明一次性购买该商品共用2 340元,问他买了多少个
21.[含评分细则](8分)如图,在矩形ABCD中,AE、BE、CG、DG分别是各内角的平分线,E、F、G、H分别为它们的交点.求证:四边形EFGH是正方形.
22.[含评分细则](2023山东济宁高新区期中)(8分)已知关于x的一元二次方程x2-2x+k+2=0有两个实数根x1,x2.
(1)求k的取值范围.
(2)若x1,x2满足=k-2,求k的值.
23.[含评分细则](2023浙江杭州上城期末)(10分)在 ABCD中,E,F为边BC上的两点,且BE=CF,AF=DE.
(1)求证:△ABF≌△DCE.
(2)求证: ABCD是矩形.
(3)连接AE,若AF是∠BAD的平分线,BE=2,AF=,求四边形ABCD的面积.
24.[含评分细则](2023山东济南钢城期末)(12分)如图,已知△ABC和△ADE,AB=AC,AD=AE,点D在BC边上,∠BAD=∠CAE,边DE与AC相交于点F.
(1)求证:△ABC∽△ADE.
(2)如果AE∥BC,DA=DC,连接CE,求证:四边形ADCE是菱形.
答案全解全析
1.C A.2x-3y+1不是等式,故不是方程;
B.该方程是三元一次方程;
C.该方程是一元二次方程;
D.该方程不是整式方程,故不是一元二次方程.
故选C.
2.A A.是最简二次根式;
B.,不是最简二次根式;
C.,不是最简二次根式;
D.,不是最简二次根式.故选A.
3.B A.∵,∴xy=6,故结论不成立;
B.∵,∴2x=3y,故结论成立;
C.∵,∴3x=2y,故结论不成立;
D.∵,∴3x=2y,故结论不成立.故选B.
4.C 根据题意可得△ABC∽△A'B'C',C,O,C'三点在同一条直线上,AB∥A'B',AO∶OA'=1∶2,故A,B,D中说法正确,C中说法错误.故选C.
5.B 不能合并,故A计算错误;
,故B计算正确;
=3,故C计算错误;
-4×,故D计算错误.
故选B.
6.C ∵矩形ABFE、矩形EFHG、矩形GHCD是全等的矩形,
∴BF=FH=CH=4,CD=AB=9,
∴BC=3BF=12.
∴BD==15.
∵EF∥GH∥CD,
∴MN=×15=5.
7.A 5 m=5 000 mm,3 m=3 000 mm,由题意,得△ADF∽△ABC,
∴,即,
∴DF=37.62 mm,∴当测试距离为3 m时,最大的“E”字的高度为37.62 mm.
故选A.
8.B 如图,连接BD.
∵四边形ABCD是菱形,∴AB=AD=CD=4,
∵∠A=60°,∴△ABD是等边三角形,
∴AB=BD,∠ABD=60°.
∵DC∥AB,∴∠CDB=∠ABD=60°.
∴∠A=∠CDB.
∵∠EBF=60°,∴∠ABE=∠DBF=60°-∠DBE,
在△ABE和△DBF中,
∴△ABE≌△DBF(ASA),∴AE=DF,
∴AE+CF=DF+CF=CD=4,
∴AE+CF的值保持不变,恒等于4.故选B.
9.A 连接CP,如图,
∵PE⊥CD,PF⊥BC,
∴∠PEC=∠PFC=90°,
∵四边形ABCD是矩形,
∴BC=AD=1,CD=AB=3,∠BCD=∠A=90°,
∵∠PEC=∠PFC=∠BCD=90°,
∴四边形PECF是矩形,∴PC=EF,当EF最小时,CP最小,
当CP⊥BD时,CP最小,
由勾股定理,得BD=,
当CP⊥BD时,S△BCD=BC·CD=BD·CP,
∴CP=,∴线段EF的最小值为,故选A.
10.C ∵四边形EBGF是正方形,EB=2,
∴FG=BG=2,∠FGB=90°,∴∠FGN=90°,
∵四边形ABCD是正方形,
∴AD=AB=4,∠BAD=90°,∴∠HAN=∠FGN,
∵H为AD的中点,∴AH=2,∴AH=FG,
又∵∠ANH=∠GNF,
∴△ANH≌△GNF(AAS),故①正确.
∵△ANH≌△GNF,∴∠AHN=∠NFG,
∵AG=AB-BG=2,∴AF=AH,
∴∠AFH≠∠AHF,∴∠AFN≠∠HFG,故②错误.
∵△ANH≌△GNF,∴AN=GN=AG=1,HN=FN,
易知四边形AGMD是矩形,∴GM=AD=4,∴=2,
又∵∠HAN=∠AGM=90°,∴△AHN∽△GMA,∴∠AHN=∠AMG,
∵AD∥GM,∴∠HAK=∠AMG,∴∠AHK=∠HAK,
∴AK=HK,易得AK=HK=NK,
又∵FN=HN,∴FN=2NK,故③正确.
∵四边形AGMD是矩形,∴DM=AG=2,
∵S△AFN=AN·FG=×1×2=1,S△ADM=AD·DM=×4×2=4,
∴S△AFN∶S△ADM=1∶4,故④正确.
故正确的结论有3个.故选C.
11. 答案 x>-5
解析 ∵二次根式有意义,∴x+5>0,
∴x>-5.
12. 答案 2a-3
解析 由题图得10,a-2<0,
∴=|a-1|-|a-2|=(a-1)-(2-a)=a-1-2+a=2a-3.
13. 答案 5
解析 如图,连接AF.
∵AB=AD,F是BD的中点,∴AF⊥BD,
又∵E是AC的中点,
∴EF=AC(直角三角形斜边上的中线等于斜边的一半),
∴AC=2EF,
∵EF=2.5,∴AC=5.
14. 答案 20
解析 ∵四边形ABCD为菱形,其边长为3,
∴AD∥BC,AB=BC=3,∴∠BAC=∠BCA,
∵AE⊥AC,∴∠EAC=90°,
∴∠BAC+∠BAE=∠BCA+∠E=90°,
∴∠BAE=∠E,∴BE=AB=3,
∴EC=BE+BC=3+3=6,
同理AF=6,∴AF=EC,
∵AD∥BC,∴四边形AECF是平行四边形,
∴ AECF的周长=2(AE+EC)=2×(4+6)=20.
15. 答案
解析 ∵∠B=36°,AB=AC,∴∠C=∠B=36°,
∴∠BAC=180°-2×36°=108°,
∵AD=CD,∴∠DAC=∠C=36°,
∴∠BAD=108°-36°=72°,∠BDA=∠DAC+∠C=72°,
∴∠BAD=∠BDA,∴AB=BD,∴AB=BD=AC,
∵∠B=∠DAC=36°,∠C=∠C,
∴△ABC∽△DAC,∴,
∴D是线段BC的黄金分割点,
∴.
16. 答案 24
解析 如图,延长FB交EA的延长线于T,
设TA=x米,EC=y米.
易知AB∥CD,
∴△TAB∽△TCD,
∴,
解得x=3,经检验,x=3是分式方程的解,
易知CD∥EF,∴△TCD∽△TEF,
∴,
解得y=24,经检验,y=24是分式方程的解,
∴EC=24米.
17.解析 (1)原式=6+3-2-4+1
=6+3-6.…………………………………………………3分
(2)∵x(2x-1)=4x-2,
∴x(2x-1)-2(2x-1)=0,
∴(x-2)(2x-1)=0,
解得x1=2,x2=. …………………………………………………………6分
18.解析 在Rt△ABC中,由勾股定理,得
AB=, ……………………………3分
∵S△ABC=AC·BC=AB·CD,
∴CD=. ………………………………………………6分
19.解析 (1)如图,△A1B1C1即为所求作的图形. ……………………………3分
A1(6,2),B1(2,4),C1(8,6). ……………………………………………………6分
(2)如图,点P的坐标为(2,4)或(1,7). ……………………………8分
20.解析 设小明一次性购买了x个该商品,
根据题意,得x=2 340, ………………………………………3分
整理,得x2-70x+936=0,
解得x1=18,x2=52, …………………………………………………………5分
∵150×10=1 500<2 340,
∴x>10,又x≤30,∴x=18, ……………………………………………………7分
∴小明一次性购买了18个该商品. …………………………………………8分
21.证明 ∵四边形ABCD是矩形,
∴∠ADC=∠BAD=90°,AD=BC, …………………………………………………2分
∵在矩形ABCD中,AE、DG分别是∠BAD和∠ADC的平分线,
∴∠ADF=∠FAD=45°,
∴∠AFD=90°,AF=DF,
∴AD=DF,∠EFG=90°, ……………………………………………………4分
同理∠FGH=∠EHG=90°,DG=CG,BC=CH,
∴四边形EFGH是矩形,DF=CH, ………………………………………………6分
∴FG=HG,
∴四边形EFGH是正方形. ……………………………………………………8分
22.解析 (1)根据题意,得Δ=(-2)2-4(k+2)≥0,
解得k≤-1,
∴k的取值范围是k≤-1. …………………………………………………3分
(2)根据题意,得x1+x2=2,x1x2=k+2,
∵x1,x2满足=k-2,
∴=k-2, …………………………………………………5分
∴k2=6,∴k=±, …………………………………………………………6分
经检验,k=±是原方程的根,
∵k≤-1,∴k=-. …………………………………………………………8分
23.解析 (1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∵BE=CF,∴BF=CE,
在△ABF和△DCE中,
∴△ABF≌△DCE(SSS). ……………………………………………………3分
(2)证明:∵△ABF≌△DCE,
∴∠B=∠C, …………………………………………………………4分
∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠B+∠C=180°,∴∠B=∠C=90°,
∴平行四边形ABCD是矩形. …………………………………………………6分
(3)∵四边形ABCD是矩形,
∴∠BAD=∠B=90°,AD∥BC,
∴∠DAF=∠BFA,
∵AF是∠BAD的平分线,
∴∠BAF=∠DAF=∠BAD=45°,∴∠BAF=∠BFA,
∴AB=BF, ………………………………………………………………………8分
∵AF=,
∵CF=BE=2,∴BC=+2,
∴四边形ABCD的面积=AB·BC=. …………10分
24.证明 (1)∵∠BAD=∠CAE,
∴∠BAD+∠CAD=∠CAE+∠CAD,即∠BAC=∠DAE, ……………………………2分
∵AB=AC,AD=AE,
∴∠B=∠ACB=(180°-∠BAC),∠ADE=∠E=(180°-∠DAE), ……………3分
∴∠B=∠ACB=∠ADE=∠E,
∴△ABC∽△ADE. …………………………………………………………5分
(2)如图,
∵AE∥BC,∴∠AEF=∠CDF,∠EAF=∠DCF,
由(1)可知∠DCF=∠ADF=∠AEF,
∴∠ADF=∠CDF,∵DA=DC,∴AF=CF,
在△AEF和△CDF中,
∴△AEF≌△CDF(AAS), ……………………………………………………8分
∴AE=CD,
又AE∥CD,∴四边形ADCE为平行四边形, …………………………………10分
∵DA=DC,∴平行四边形ADCE为菱形. ……………………………12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024五四制鲁教版数学八年级下学期
期末素养综合测试(一)
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.(2023山东济宁高新区期中)下列是一元二次方程的是(( )
A.2x-3y+1 B.3x+y=z
C.x2-5x=1 D.x2-+2=0
2.(2023山东威海环翠期中)下列各式是最简二次根式的是( )
A.
3.(2023山东济南莱芜陈毅中学期中)已知2x=3y(y≠0),则下面结论成立的是( )
A.
C.
4.如图,以点O为位似中心,把△ABC各边扩大为原来的2倍得到△A'B'C'.以下说法中错误的是( )
A.△ABC∽△A'B'C'
B.C,O,C'三点在同一条直线上
C.AO∶AA'=1∶2
D.AB∥A'B'
5.(2022山东聊城东昌府一模)下列计算正确的是 ( )
A.
C.
6.【新独家原创】如图,将三个全等的矩形拼成一个大矩形ABCD,连接BD,与EF,GH分别交于M,N两点.若AB=9,BF=4,则线段MN的长为( )
A.3 B.4
C.5 D.6
7.(2023山东烟台招远期末)如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5 m时,标准视力表中最大的“E”字的高度为62.7 mm,当测试距离为3 m时,最大的“E”字的高度为( )
A.37.62 mm B.43 mm
C.43.62 mm D.104.5 mm
8.(2023山东威海文登期中)如图,在边长为4的菱形ABCD中,∠A=60°,E,F分别为AD,DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的值( )
A.逐渐增大 B.恒等于4
C.先减小再增大 D.恒等于2
9.如图,在矩形ABCD中,AD=1,AB=3,点P为线段BD上一动点,PE⊥CD于点E,PF⊥BC于点F,则线段EF的最小值为( )
A.
10.如图,正方形ABCD的边长为4,延长CB至E,使EB=2,以EB为边在其上方作正方形EBGF,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH,分别与AB,AM交于点N,K,则下列结论:①△ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;
④S△AFN∶S△ADM=1∶4.其中正确的个数为 ( )
A.1 B.2
C.3 D.4
二、填空题(每小题4分,共24分)
11.(2023山东泰安十五中月考)二次根式有意义,那么x的取值范围是 .
12.(2023山东聊城临清期末)已知实数a在数轴上对应的点的位置如图所示,则化简的结果是 .
13.(2021辽宁沈阳模拟)如图,在△ABC中,点D在BC边上,AB=AD,点E,F分别是AC,BD的中点,EF=2.5,则AC的长为 .
14.(2023山东济南莱芜胜利中学期中)如图,菱形ABCD的边长为3,过点A、C作对角线AC的垂线,分别交CB和AD的延长线于点E、F,AE=4,则四边形AECF的周长为 .
15.(2021山东淄博桓台期末)在△ABC中,∠B=36°,AB=AC,D是BC上一点,满足AD=CD,则= .
16.如图,小明用相似图形的知识测量旗杆高度,已知小明的眼睛离地面1.5米(AB=1.5米),他将3米长的标杆CD竖直放置在身前3米处(AC=3米),此时小明的眼睛、标杆的顶端、旗杆的顶端在一条直线上,通过计算得旗杆的高度为15米(EF=15米),则旗杆和标杆之间的水平距离CE为 米.
三、解答题(共66分)
17.[含评分细则](6分)
(1)(2023山东济宁任城期中)计算:(.
(2)解方程:x(2x-1)=4x-2.
18.[含评分细则](2023山东烟台莱州期中)(6分)已知∠ACB=90°,
BC=2,CD是AB边上的高,求CD的长.
19.[含评分细则](2021辽宁抚顺新抚一模)(8分)如图,△ABC的三个顶点的坐标分别为A(3,1),B(1,2),C(4,3).
(1)以原点O为位似中心,在第一象限内将△ABC的各边放大为原来的2倍得到△A1B1C1,作出△A1B1C1,写出A1,B1,C1的坐标.
(2)若P为第一象限内的整点(横、纵坐标都是整数的点),AP平分∠BAC,直接写出点P的坐标.
20.[含评分细则](2023山东青岛莱西期中)(8分)某商场促销一种商品,促销方式如下:
1.售价为150元/个; 2.若购买数量超过10个,则单价按每增加2个减5元的方式计算; 3.一次性购买不得超过30个.
小明一次性购买该商品共用2 340元,问他买了多少个
21.[含评分细则](8分)如图,在矩形ABCD中,AE、BE、CG、DG分别是各内角的平分线,E、F、G、H分别为它们的交点.求证:四边形EFGH是正方形.
22.[含评分细则](2023山东济宁高新区期中)(8分)已知关于x的一元二次方程x2-2x+k+2=0有两个实数根x1,x2.
(1)求k的取值范围.
(2)若x1,x2满足=k-2,求k的值.
23.[含评分细则](2023浙江杭州上城期末)(10分)在 ABCD中,E,F为边BC上的两点,且BE=CF,AF=DE.
(1)求证:△ABF≌△DCE.
(2)求证: ABCD是矩形.
(3)连接AE,若AF是∠BAD的平分线,BE=2,AF=,求四边形ABCD的面积.
24.[含评分细则](2023山东济南钢城期末)(12分)如图,已知△ABC和△ADE,AB=AC,AD=AE,点D在BC边上,∠BAD=∠CAE,边DE与AC相交于点F.
(1)求证:△ABC∽△ADE.
(2)如果AE∥BC,DA=DC,连接CE,求证:四边形ADCE是菱形.
答案全解全析
1.C A.2x-3y+1不是等式,故不是方程;
B.该方程是三元一次方程;
C.该方程是一元二次方程;
D.该方程不是整式方程,故不是一元二次方程.
故选C.
2.A A.是最简二次根式;
B.,不是最简二次根式;
C.,不是最简二次根式;
D.,不是最简二次根式.故选A.
3.B A.∵,∴xy=6,故结论不成立;
B.∵,∴2x=3y,故结论成立;
C.∵,∴3x=2y,故结论不成立;
D.∵,∴3x=2y,故结论不成立.故选B.
4.C 根据题意可得△ABC∽△A'B'C',C,O,C'三点在同一条直线上,AB∥A'B',AO∶OA'=1∶2,故A,B,D中说法正确,C中说法错误.故选C.
5.B 不能合并,故A计算错误;
,故B计算正确;
=3,故C计算错误;
-4×,故D计算错误.
故选B.
6.C ∵矩形ABFE、矩形EFHG、矩形GHCD是全等的矩形,
∴BF=FH=CH=4,CD=AB=9,
∴BC=3BF=12.
∴BD==15.
∵EF∥GH∥CD,
∴MN=×15=5.
7.A 5 m=5 000 mm,3 m=3 000 mm,由题意,得△ADF∽△ABC,
∴,即,
∴DF=37.62 mm,∴当测试距离为3 m时,最大的“E”字的高度为37.62 mm.
故选A.
8.B 如图,连接BD.
∵四边形ABCD是菱形,∴AB=AD=CD=4,
∵∠A=60°,∴△ABD是等边三角形,
∴AB=BD,∠ABD=60°.
∵DC∥AB,∴∠CDB=∠ABD=60°.
∴∠A=∠CDB.
∵∠EBF=60°,∴∠ABE=∠DBF=60°-∠DBE,
在△ABE和△DBF中,
∴△ABE≌△DBF(ASA),∴AE=DF,
∴AE+CF=DF+CF=CD=4,
∴AE+CF的值保持不变,恒等于4.故选B.
9.A 连接CP,如图,
∵PE⊥CD,PF⊥BC,
∴∠PEC=∠PFC=90°,
∵四边形ABCD是矩形,
∴BC=AD=1,CD=AB=3,∠BCD=∠A=90°,
∵∠PEC=∠PFC=∠BCD=90°,
∴四边形PECF是矩形,∴PC=EF,当EF最小时,CP最小,
当CP⊥BD时,CP最小,
由勾股定理,得BD=,
当CP⊥BD时,S△BCD=BC·CD=BD·CP,
∴CP=,∴线段EF的最小值为,故选A.
10.C ∵四边形EBGF是正方形,EB=2,
∴FG=BG=2,∠FGB=90°,∴∠FGN=90°,
∵四边形ABCD是正方形,
∴AD=AB=4,∠BAD=90°,∴∠HAN=∠FGN,
∵H为AD的中点,∴AH=2,∴AH=FG,
又∵∠ANH=∠GNF,
∴△ANH≌△GNF(AAS),故①正确.
∵△ANH≌△GNF,∴∠AHN=∠NFG,
∵AG=AB-BG=2,∴AF=AH,
∴∠AFH≠∠AHF,∴∠AFN≠∠HFG,故②错误.
∵△ANH≌△GNF,∴AN=GN=AG=1,HN=FN,
易知四边形AGMD是矩形,∴GM=AD=4,∴=2,
又∵∠HAN=∠AGM=90°,∴△AHN∽△GMA,∴∠AHN=∠AMG,
∵AD∥GM,∴∠HAK=∠AMG,∴∠AHK=∠HAK,
∴AK=HK,易得AK=HK=NK,
又∵FN=HN,∴FN=2NK,故③正确.
∵四边形AGMD是矩形,∴DM=AG=2,
∵S△AFN=AN·FG=×1×2=1,S△ADM=AD·DM=×4×2=4,
∴S△AFN∶S△ADM=1∶4,故④正确.
故正确的结论有3个.故选C.
11. 答案 x>-5
解析 ∵二次根式有意义,∴x+5>0,
∴x>-5.
12. 答案 2a-3
解析 由题图得1
∴=|a-1|-|a-2|=(a-1)-(2-a)=a-1-2+a=2a-3.
13. 答案 5
解析 如图,连接AF.
∵AB=AD,F是BD的中点,∴AF⊥BD,
又∵E是AC的中点,
∴EF=AC(直角三角形斜边上的中线等于斜边的一半),
∴AC=2EF,
∵EF=2.5,∴AC=5.
14. 答案 20
解析 ∵四边形ABCD为菱形,其边长为3,
∴AD∥BC,AB=BC=3,∴∠BAC=∠BCA,
∵AE⊥AC,∴∠EAC=90°,
∴∠BAC+∠BAE=∠BCA+∠E=90°,
∴∠BAE=∠E,∴BE=AB=3,
∴EC=BE+BC=3+3=6,
同理AF=6,∴AF=EC,
∵AD∥BC,∴四边形AECF是平行四边形,
∴ AECF的周长=2(AE+EC)=2×(4+6)=20.
15. 答案
解析 ∵∠B=36°,AB=AC,∴∠C=∠B=36°,
∴∠BAC=180°-2×36°=108°,
∵AD=CD,∴∠DAC=∠C=36°,
∴∠BAD=108°-36°=72°,∠BDA=∠DAC+∠C=72°,
∴∠BAD=∠BDA,∴AB=BD,∴AB=BD=AC,
∵∠B=∠DAC=36°,∠C=∠C,
∴△ABC∽△DAC,∴,
∴D是线段BC的黄金分割点,
∴.
16. 答案 24
解析 如图,延长FB交EA的延长线于T,
设TA=x米,EC=y米.
易知AB∥CD,
∴△TAB∽△TCD,
∴,
解得x=3,经检验,x=3是分式方程的解,
易知CD∥EF,∴△TCD∽△TEF,
∴,
解得y=24,经检验,y=24是分式方程的解,
∴EC=24米.
17.解析 (1)原式=6+3-2-4+1
=6+3-6.…………………………………………………3分
(2)∵x(2x-1)=4x-2,
∴x(2x-1)-2(2x-1)=0,
∴(x-2)(2x-1)=0,
解得x1=2,x2=. …………………………………………………………6分
18.解析 在Rt△ABC中,由勾股定理,得
AB=, ……………………………3分
∵S△ABC=AC·BC=AB·CD,
∴CD=. ………………………………………………6分
19.解析 (1)如图,△A1B1C1即为所求作的图形. ……………………………3分
A1(6,2),B1(2,4),C1(8,6). ……………………………………………………6分
(2)如图,点P的坐标为(2,4)或(1,7). ……………………………8分
20.解析 设小明一次性购买了x个该商品,
根据题意,得x=2 340, ………………………………………3分
整理,得x2-70x+936=0,
解得x1=18,x2=52, …………………………………………………………5分
∵150×10=1 500<2 340,
∴x>10,又x≤30,∴x=18, ……………………………………………………7分
∴小明一次性购买了18个该商品. …………………………………………8分
21.证明 ∵四边形ABCD是矩形,
∴∠ADC=∠BAD=90°,AD=BC, …………………………………………………2分
∵在矩形ABCD中,AE、DG分别是∠BAD和∠ADC的平分线,
∴∠ADF=∠FAD=45°,
∴∠AFD=90°,AF=DF,
∴AD=DF,∠EFG=90°, ……………………………………………………4分
同理∠FGH=∠EHG=90°,DG=CG,BC=CH,
∴四边形EFGH是矩形,DF=CH, ………………………………………………6分
∴FG=HG,
∴四边形EFGH是正方形. ……………………………………………………8分
22.解析 (1)根据题意,得Δ=(-2)2-4(k+2)≥0,
解得k≤-1,
∴k的取值范围是k≤-1. …………………………………………………3分
(2)根据题意,得x1+x2=2,x1x2=k+2,
∵x1,x2满足=k-2,
∴=k-2, …………………………………………………5分
∴k2=6,∴k=±, …………………………………………………………6分
经检验,k=±是原方程的根,
∵k≤-1,∴k=-. …………………………………………………………8分
23.解析 (1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∵BE=CF,∴BF=CE,
在△ABF和△DCE中,
∴△ABF≌△DCE(SSS). ……………………………………………………3分
(2)证明:∵△ABF≌△DCE,
∴∠B=∠C, …………………………………………………………4分
∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠B+∠C=180°,∴∠B=∠C=90°,
∴平行四边形ABCD是矩形. …………………………………………………6分
(3)∵四边形ABCD是矩形,
∴∠BAD=∠B=90°,AD∥BC,
∴∠DAF=∠BFA,
∵AF是∠BAD的平分线,
∴∠BAF=∠DAF=∠BAD=45°,∴∠BAF=∠BFA,
∴AB=BF, ………………………………………………………………………8分
∵AF=,
∵CF=BE=2,∴BC=+2,
∴四边形ABCD的面积=AB·BC=. …………10分
24.证明 (1)∵∠BAD=∠CAE,
∴∠BAD+∠CAD=∠CAE+∠CAD,即∠BAC=∠DAE, ……………………………2分
∵AB=AC,AD=AE,
∴∠B=∠ACB=(180°-∠BAC),∠ADE=∠E=(180°-∠DAE), ……………3分
∴∠B=∠ACB=∠ADE=∠E,
∴△ABC∽△ADE. …………………………………………………………5分
(2)如图,
∵AE∥BC,∴∠AEF=∠CDF,∠EAF=∠DCF,
由(1)可知∠DCF=∠ADF=∠AEF,
∴∠ADF=∠CDF,∵DA=DC,∴AF=CF,
在△AEF和△CDF中,
∴△AEF≌△CDF(AAS), ……………………………………………………8分
∴AE=CD,
又AE∥CD,∴四边形ADCE为平行四边形, …………………………………10分
∵DA=DC,∴平行四边形ADCE为菱形. ……………………………12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
