2024五四制鲁教版数学八年级下学期--期中素养综合测试(含解析)
文档属性
| 名称 | 2024五四制鲁教版数学八年级下学期--期中素养综合测试(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 435.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:38:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024五四制鲁教版数学八年级下学期
期中素养综合测试
(满分120分,限时100分钟)
一、选择题(每小题4分,共32分)
1.(2023浙江丽水期末)下列式子一定不是二次根式的是( )
A.
C.
2.(2023山东泰安十五中月考)下列二次根式中属于最简二次根式的是( )
A.
3.(2023广东广州番禺一模)下列计算正确的是( )
A.=-2
C.=±2
4.(2023山东东营广饶四校联考)下列二次根式中,与是同类二次根式的是( )
A.
5.(2021山东聊城阳谷月考)若有理数x,y满足y=+1,则x-y的平方根是( )
A.1 B.±1 C.-1 D.无法确定
6.(2022山东德州宁津期中)如图,在平行四边形ABCD中,M、N是对角线BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件可以是( )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
7.(2023安徽蚌埠蚌山模拟)如果f(x)=并且f()表示当x=时的值,即f(表示当x=时的值,即f,那么f(+…+f(的值是( )
A.n-
8.(2023重庆合川期末)如图,在菱形ABCD中,过点C作AD的垂线与∠ABD的平分线交于点E,若BC=CE,则∠A的度数为 ( )
A.135° B.115° C.150° D.120°
二、填空题(每小题4分,共24分)
9.(2023湖南常德中考)要使二次根式有意义,则x应满足的条件是 .
10.【易错题】(2022福建福州福清月考)计算:2÷=
.
11.(2023广东佛山二模)实数a在数轴上对应的点的位置如图所示,则化简|a-1|-的结果是 .
12.【真实情境】(2023江西赣州期末)如图,三位同学分别站在直角三角形ABC的三个顶点处做投圈游戏,目标物放在斜边AC的中点O处,已知AC=6 m,则点B到目标物的距离是 m.
13.(2023湖南长沙期末)如图,在矩形ABCD中,AE平分∠BAD,∠CAE=15°,那么∠BOE的度数为 .
14.(2022浙江杭州上城期末)如图,在正方形ABCD中,AB=3,E是AD边上的点,AE=2,连接BE,过A作AF⊥BE交DC于F,连接EF,则EF= .
三、解答题(共64分)
15.[含评分细则](2023山东威海经开区期中)(10分)计算:
(1).
(2)(+1)2- (--1).
16.[含评分细则](2023海南澄迈月考)(8分)已知长方形的长为a,宽为b,且a=,请解决下列问题:
(1)求这个长方形的周长.
(2)若一个正方形的面积和这个长方形的面积相等,求这个正方形的边长.
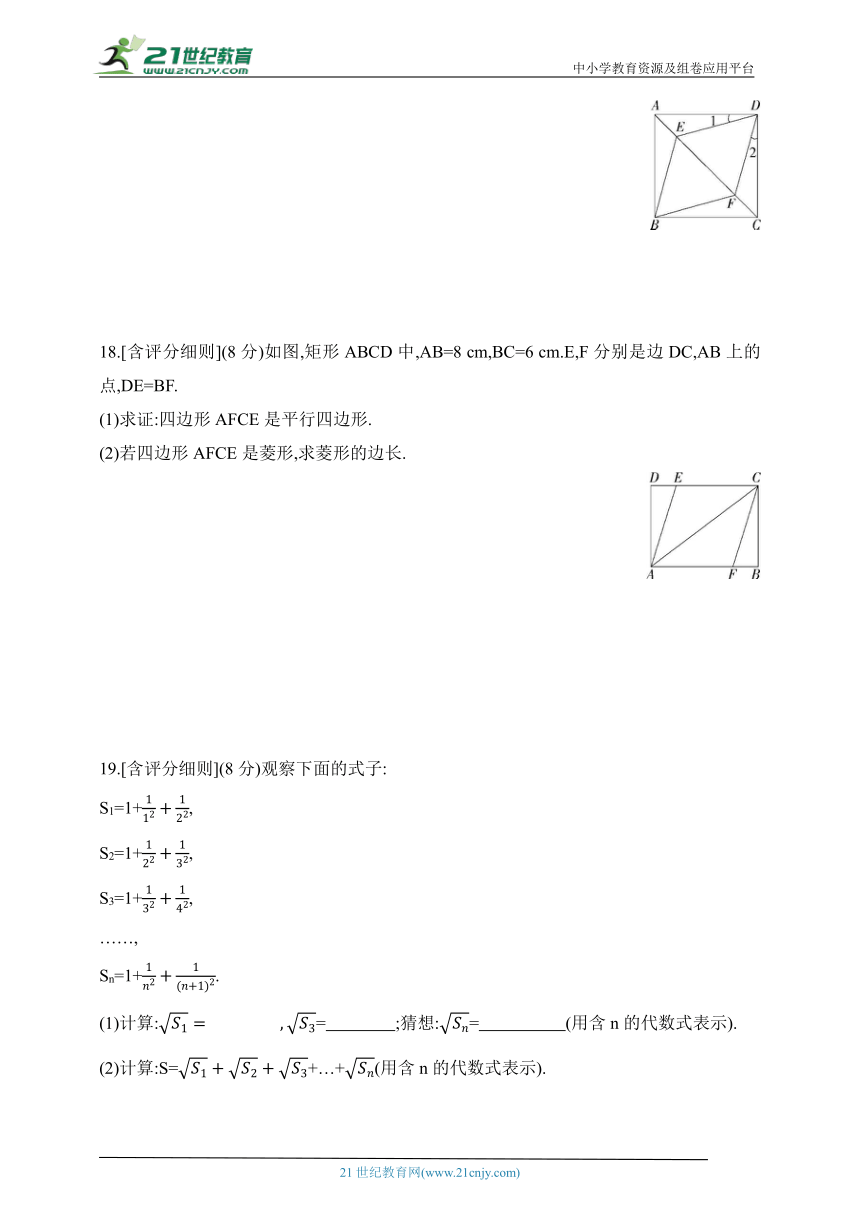
17.[含评分细则]【新独家原创】(8分)如图,正方形ABCD中,E,F是对角线AC上的两点,连接BE,BF,DE,DF,若∠1=∠2,求证:四边形BEDF是菱形.
18.[含评分细则](8分)如图,矩形ABCD中,AB=8 cm,BC=6 cm.E,F分别是边DC,AB上的点,DE=BF.
(1)求证:四边形AFCE是平行四边形.
(2)若四边形AFCE是菱形,求菱形的边长.
19.[含评分细则](8分)观察下面的式子:
S1=1+,
S2=1+,
S3=1+,
……,
Sn=1+.
(1)计算:= ;猜想:= (用含n的代数式表示).
(2)计算:S=+…+(用含n的代数式表示).
20.[含评分细则](2022北京朝阳二模)(10分)如图,在菱形ABCD中,O为AC,BD的交点,P,M,N分别为CD,OD,OC的中点.
(1)求证:四边形OMPN是矩形.
(2)连接AP,若AB=4,∠BAD=60°,求AP的长.
21.[含评分细则](2023山东淄博柳泉中学期中)(12分)如图,已知△ABC,点O是边AC上的一个动点,过O作直线MN∥BC,MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.
(1)探究线段OE与OF的数量关系,并说明理由.
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形 请说明理由.
答案全解全析
1.D 中-2<0,不是二次根式,故选D.
2.A A.是最简二次根式;B.,不是最简二次根式;C.的被开方数中含有分母,不是最简二次根式;D.,不是最简二次根式,故选A.
3.A A.=2,计算正确;B.=2,计算错误;C.=-2,计算错误;
D.=2,计算错误.故选A.
4.D A.,与的被开方数不同,不是同类二次根式;B.,与的被开方数不同,不是同类二次根式;C.,与的被开方数不同,
不是同类二次根式;D.,与的被开方数相同,是同类二次根式.
故选D.
5.B ∵y=
∴x=2,∴y=1,∴x-y=2-1=1,
故x-y的平方根是±1.故选B.
6.A ∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BM=DN,∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形,
当添加OM=AC时,OM=OA,∴MN=AC,
∴四边形AMCN是矩形.
故选A.
7.A 代入计算可得f(=1,……,
∴f(=1,
∴原式=.
故选A.
8.D ∵四边形ABCD是菱形,
∴∠ABD=∠CBD,AD∥BC,
∴∠A+∠ABC=180°,
∵CE⊥AD,∴CE⊥BC,∴∠BCE=90°,
∵BC=CE,
∴△BCE是等腰直角三角形,
∴∠CBE=45°,
∵BE平分∠ABD,
∴∠ABE=∠DBE=∠ABD=∠CBD,
∴∠CBD+∠CBD=45°,
∴∠CBD=30°,∴∠ABC=2∠CBD=60°,
∴∠A=180°-∠ABC=180°-60°=120°,
故选D.
9. 答案 x≥4
解析 根据题意,得x-4≥0,解得x≥4.
10. 答案
解析 本题易产生不按运算顺序计算的错误.
原式=2×.
11. 答案 1-2a
解析 根据数轴可知a-1<0,a>0,
所以原式=1-a-a=1-2a.
12. 答案 3
解析 ∵∠ABC=90°,点O是斜边AC的中点,
∴BO=AC=3 m.
13. 答案 75°
解析 ∵四边形ABCD是矩形,∴∠ABC=∠BAD=90°,OA=OB,
∵AE平分∠BAD,∴∠BAE=∠EAD=45°,
∵∠EAO=15°,∴∠OAB=60°,
∵OA=OB,∴△BOA为等边三角形,∠ABO=60°,
∴BA=BO,∠EBO=30°,
∵∠BAE=45°,∠ABC=90°,
∴△BAE为等腰直角三角形,∴BA=BE.
∴BE=BO,∴∠BOE=∠BEO=(180°-∠EBO)=75°.
14. 答案
解析 ∵四边形ABCD是正方形,
∴AD=AB=3,∠BAE=∠ADF=90°,
∴∠DAF+∠AFD=90°,
∵AF⊥BE,∴∠AEB+∠DAF=90°,∴∠DFA=∠AEB.
在△ABE和△DAF中,
∴△ABE≌△DAF(AAS),∴DF=AE=2,
∵AD=3,AE=2,∴DE=AD-AE=3-2=1,
在Rt△DEF中,EF=.
15.解析 (1)
=
=8
=8×-2×3=2-6=-4.…………………………………………………………5分
(2)(-1)
=2+2+1-(3-1)
=2+2. ……………………………………………10分
16.解析 (1)这个长方形的周长=2×()
=2×(4. ……………………………………………4分
(2)这个正方形的面积==16,
∴这个正方形的边长为=4. ……………………………………………8分
17.证明 ∵四边形ABCD是正方形,
∴∠ACD=∠ACB=∠BAC=∠DAC=45°,BC=CD=AD=AB,
∵CF=CF,AE=AE,
∴△CDF≌△CBF,△DAE≌△BAE,
∴BF=FD,BE=ED, …………………………………………………………4分
∵∠1=∠2,AD=CD,∠DAE=∠DCF,
∴△DAE≌△DCF,
∴DE=DF, …………………………………………………………………6分
∴BF=FD=BE=ED,
∴四边形BEDF是菱形. ……………………………………………………8分
18.解析 (1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD, ……………………………………………………2分
∵DE=BF,∴CD-DE=AB-BF,
∴CE=AF,∵CE∥AF,
∴四边形AFCE是平行四边形. ………………………………………4分
(2)∵四边形AFCE是菱形,
∴AE=CE=AF=CF,
设AE=CE=x,则DE=8-x,
在Rt△ADE中,由勾股定理,得AD2+DE2=AE2,
即62+(8-x)2=x2, ……………………………………………………6分
解得x=6.25,即AE=CE=CF=AF=6.25,
∴菱形AFCE的边长是6.25. ………………………………………8分
19.解析 (1). …………4分(前两个空每空1分,第三个空2分)
∵S1=1+.
∵S3=1+.
∵Sn=1+,
∴.
(2)S=+…+
=1++…+1+
=n+
=n+1-. ……………………………………………………………8分
20.解析 (1)证明:∵P,M,N分别为CD,OD,OC的中点,
∴PM,PN是△OCD的中位线,
∴PM∥OC,PN∥OD,
∴四边形OMPN是平行四边形, ………………………………………2分
∵四边形ABCD是菱形,
∴AC⊥BD,∴∠MON=90°,
∴四边形OMPN是矩形. ……………………………………………………4分
(2)如图,∵四边形ABCD是菱形,
∴AB=AD,OA=OC,OB=OD,AC⊥BD,
∵∠BAD=60°,∴△ABD是等边三角形,
∴AD=BD=AB=4,∴OD=BD=2. …………………………………………………6分
在Rt△OAD中,由勾股定理,得OA=
.
∵M,N分别为OD,OC的中点,
∴OM=,
∴AN=OA+ON=3. ………………………………………………………………8分
由(1)可知,四边形OMPN是矩形,
∴NP=OM=1,∠PNA=90°,
∴在Rt△ANP中,AP=. ……………10分
21.解析 (1)OE=OF. ……………………………………………………1分
理由:∵CE是∠ACB的平分线,
∴∠ACE=∠BCE,
∵MN∥BC,∴∠NEC=∠ECB,
∴∠NEC=∠ACE,
∴OE=OC, …………………………………………………………………3分
∵CF是∠ACD的平分线,∴∠OCF=∠FCD,
∵MN∥BC,∴∠OFC=∠FCD,
∴∠OFC=∠OCF,
∴OF=OC, …………………………………………………………………5分
∴OE=OF. …………………………………………………………………6分
(2)当点O运动到AC的中点,且△ABC是以∠ACB为直角的直角三角形时,四边形AECF是正方形. ……………………………………………………7分
理由:∵点O是AC的中点,∴AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形, ………………………………………………8分
∵FO=CO,∴AO=CO=EO=FO,
∴四边形AECF是矩形. ……………………………………………………10分
∵MN∥BC,∠ACB=90°,
∴∠AOE=90°,∴AC⊥EF,
∴四边形AECF是正方形. ……………………………………………………12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024五四制鲁教版数学八年级下学期
期中素养综合测试
(满分120分,限时100分钟)
一、选择题(每小题4分,共32分)
1.(2023浙江丽水期末)下列式子一定不是二次根式的是( )
A.
C.
2.(2023山东泰安十五中月考)下列二次根式中属于最简二次根式的是( )
A.
3.(2023广东广州番禺一模)下列计算正确的是( )
A.=-2
C.=±2
4.(2023山东东营广饶四校联考)下列二次根式中,与是同类二次根式的是( )
A.
5.(2021山东聊城阳谷月考)若有理数x,y满足y=+1,则x-y的平方根是( )
A.1 B.±1 C.-1 D.无法确定
6.(2022山东德州宁津期中)如图,在平行四边形ABCD中,M、N是对角线BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件可以是( )
A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND
7.(2023安徽蚌埠蚌山模拟)如果f(x)=并且f()表示当x=时的值,即f(表示当x=时的值,即f,那么f(+…+f(的值是( )
A.n-
8.(2023重庆合川期末)如图,在菱形ABCD中,过点C作AD的垂线与∠ABD的平分线交于点E,若BC=CE,则∠A的度数为 ( )
A.135° B.115° C.150° D.120°
二、填空题(每小题4分,共24分)
9.(2023湖南常德中考)要使二次根式有意义,则x应满足的条件是 .
10.【易错题】(2022福建福州福清月考)计算:2÷=
.
11.(2023广东佛山二模)实数a在数轴上对应的点的位置如图所示,则化简|a-1|-的结果是 .
12.【真实情境】(2023江西赣州期末)如图,三位同学分别站在直角三角形ABC的三个顶点处做投圈游戏,目标物放在斜边AC的中点O处,已知AC=6 m,则点B到目标物的距离是 m.
13.(2023湖南长沙期末)如图,在矩形ABCD中,AE平分∠BAD,∠CAE=15°,那么∠BOE的度数为 .
14.(2022浙江杭州上城期末)如图,在正方形ABCD中,AB=3,E是AD边上的点,AE=2,连接BE,过A作AF⊥BE交DC于F,连接EF,则EF= .
三、解答题(共64分)
15.[含评分细则](2023山东威海经开区期中)(10分)计算:
(1).
(2)(+1)2- (--1).
16.[含评分细则](2023海南澄迈月考)(8分)已知长方形的长为a,宽为b,且a=,请解决下列问题:
(1)求这个长方形的周长.
(2)若一个正方形的面积和这个长方形的面积相等,求这个正方形的边长.
17.[含评分细则]【新独家原创】(8分)如图,正方形ABCD中,E,F是对角线AC上的两点,连接BE,BF,DE,DF,若∠1=∠2,求证:四边形BEDF是菱形.
18.[含评分细则](8分)如图,矩形ABCD中,AB=8 cm,BC=6 cm.E,F分别是边DC,AB上的点,DE=BF.
(1)求证:四边形AFCE是平行四边形.
(2)若四边形AFCE是菱形,求菱形的边长.
19.[含评分细则](8分)观察下面的式子:
S1=1+,
S2=1+,
S3=1+,
……,
Sn=1+.
(1)计算:= ;猜想:= (用含n的代数式表示).
(2)计算:S=+…+(用含n的代数式表示).
20.[含评分细则](2022北京朝阳二模)(10分)如图,在菱形ABCD中,O为AC,BD的交点,P,M,N分别为CD,OD,OC的中点.
(1)求证:四边形OMPN是矩形.
(2)连接AP,若AB=4,∠BAD=60°,求AP的长.
21.[含评分细则](2023山东淄博柳泉中学期中)(12分)如图,已知△ABC,点O是边AC上的一个动点,过O作直线MN∥BC,MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.
(1)探究线段OE与OF的数量关系,并说明理由.
(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形 请说明理由.
答案全解全析
1.D 中-2<0,不是二次根式,故选D.
2.A A.是最简二次根式;B.,不是最简二次根式;C.的被开方数中含有分母,不是最简二次根式;D.,不是最简二次根式,故选A.
3.A A.=2,计算正确;B.=2,计算错误;C.=-2,计算错误;
D.=2,计算错误.故选A.
4.D A.,与的被开方数不同,不是同类二次根式;B.,与的被开方数不同,不是同类二次根式;C.,与的被开方数不同,
不是同类二次根式;D.,与的被开方数相同,是同类二次根式.
故选D.
5.B ∵y=
∴x=2,∴y=1,∴x-y=2-1=1,
故x-y的平方根是±1.故选B.
6.A ∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BM=DN,∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形,
当添加OM=AC时,OM=OA,∴MN=AC,
∴四边形AMCN是矩形.
故选A.
7.A 代入计算可得f(=1,……,
∴f(=1,
∴原式=.
故选A.
8.D ∵四边形ABCD是菱形,
∴∠ABD=∠CBD,AD∥BC,
∴∠A+∠ABC=180°,
∵CE⊥AD,∴CE⊥BC,∴∠BCE=90°,
∵BC=CE,
∴△BCE是等腰直角三角形,
∴∠CBE=45°,
∵BE平分∠ABD,
∴∠ABE=∠DBE=∠ABD=∠CBD,
∴∠CBD+∠CBD=45°,
∴∠CBD=30°,∴∠ABC=2∠CBD=60°,
∴∠A=180°-∠ABC=180°-60°=120°,
故选D.
9. 答案 x≥4
解析 根据题意,得x-4≥0,解得x≥4.
10. 答案
解析 本题易产生不按运算顺序计算的错误.
原式=2×.
11. 答案 1-2a
解析 根据数轴可知a-1<0,a>0,
所以原式=1-a-a=1-2a.
12. 答案 3
解析 ∵∠ABC=90°,点O是斜边AC的中点,
∴BO=AC=3 m.
13. 答案 75°
解析 ∵四边形ABCD是矩形,∴∠ABC=∠BAD=90°,OA=OB,
∵AE平分∠BAD,∴∠BAE=∠EAD=45°,
∵∠EAO=15°,∴∠OAB=60°,
∵OA=OB,∴△BOA为等边三角形,∠ABO=60°,
∴BA=BO,∠EBO=30°,
∵∠BAE=45°,∠ABC=90°,
∴△BAE为等腰直角三角形,∴BA=BE.
∴BE=BO,∴∠BOE=∠BEO=(180°-∠EBO)=75°.
14. 答案
解析 ∵四边形ABCD是正方形,
∴AD=AB=3,∠BAE=∠ADF=90°,
∴∠DAF+∠AFD=90°,
∵AF⊥BE,∴∠AEB+∠DAF=90°,∴∠DFA=∠AEB.
在△ABE和△DAF中,
∴△ABE≌△DAF(AAS),∴DF=AE=2,
∵AD=3,AE=2,∴DE=AD-AE=3-2=1,
在Rt△DEF中,EF=.
15.解析 (1)
=
=8
=8×-2×3=2-6=-4.…………………………………………………………5分
(2)(-1)
=2+2+1-(3-1)
=2+2. ……………………………………………10分
16.解析 (1)这个长方形的周长=2×()
=2×(4. ……………………………………………4分
(2)这个正方形的面积==16,
∴这个正方形的边长为=4. ……………………………………………8分
17.证明 ∵四边形ABCD是正方形,
∴∠ACD=∠ACB=∠BAC=∠DAC=45°,BC=CD=AD=AB,
∵CF=CF,AE=AE,
∴△CDF≌△CBF,△DAE≌△BAE,
∴BF=FD,BE=ED, …………………………………………………………4分
∵∠1=∠2,AD=CD,∠DAE=∠DCF,
∴△DAE≌△DCF,
∴DE=DF, …………………………………………………………………6分
∴BF=FD=BE=ED,
∴四边形BEDF是菱形. ……………………………………………………8分
18.解析 (1)证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD, ……………………………………………………2分
∵DE=BF,∴CD-DE=AB-BF,
∴CE=AF,∵CE∥AF,
∴四边形AFCE是平行四边形. ………………………………………4分
(2)∵四边形AFCE是菱形,
∴AE=CE=AF=CF,
设AE=CE=x,则DE=8-x,
在Rt△ADE中,由勾股定理,得AD2+DE2=AE2,
即62+(8-x)2=x2, ……………………………………………………6分
解得x=6.25,即AE=CE=CF=AF=6.25,
∴菱形AFCE的边长是6.25. ………………………………………8分
19.解析 (1). …………4分(前两个空每空1分,第三个空2分)
∵S1=1+.
∵S3=1+.
∵Sn=1+,
∴.
(2)S=+…+
=1++…+1+
=n+
=n+1-. ……………………………………………………………8分
20.解析 (1)证明:∵P,M,N分别为CD,OD,OC的中点,
∴PM,PN是△OCD的中位线,
∴PM∥OC,PN∥OD,
∴四边形OMPN是平行四边形, ………………………………………2分
∵四边形ABCD是菱形,
∴AC⊥BD,∴∠MON=90°,
∴四边形OMPN是矩形. ……………………………………………………4分
(2)如图,∵四边形ABCD是菱形,
∴AB=AD,OA=OC,OB=OD,AC⊥BD,
∵∠BAD=60°,∴△ABD是等边三角形,
∴AD=BD=AB=4,∴OD=BD=2. …………………………………………………6分
在Rt△OAD中,由勾股定理,得OA=
.
∵M,N分别为OD,OC的中点,
∴OM=,
∴AN=OA+ON=3. ………………………………………………………………8分
由(1)可知,四边形OMPN是矩形,
∴NP=OM=1,∠PNA=90°,
∴在Rt△ANP中,AP=. ……………10分
21.解析 (1)OE=OF. ……………………………………………………1分
理由:∵CE是∠ACB的平分线,
∴∠ACE=∠BCE,
∵MN∥BC,∴∠NEC=∠ECB,
∴∠NEC=∠ACE,
∴OE=OC, …………………………………………………………………3分
∵CF是∠ACD的平分线,∴∠OCF=∠FCD,
∵MN∥BC,∴∠OFC=∠FCD,
∴∠OFC=∠OCF,
∴OF=OC, …………………………………………………………………5分
∴OE=OF. …………………………………………………………………6分
(2)当点O运动到AC的中点,且△ABC是以∠ACB为直角的直角三角形时,四边形AECF是正方形. ……………………………………………………7分
理由:∵点O是AC的中点,∴AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形, ………………………………………………8分
∵FO=CO,∴AO=CO=EO=FO,
∴四边形AECF是矩形. ……………………………………………………10分
∵MN∥BC,∠ACB=90°,
∴∠AOE=90°,∴AC⊥EF,
∴四边形AECF是正方形. ……………………………………………………12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
