数学人教A版(2019)必修第一册5.2.1三角函数的概念(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.2.1三角函数的概念(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 17:10:30 | ||
图片预览



文档简介
(共21张PPT)
5.2.1三角函数的概念
引导语:在客观世界中存在大量循环往复、周而复始的周期现象,比如日出日落、钟摆运动等,匀速圆周运动是这类现象的代表
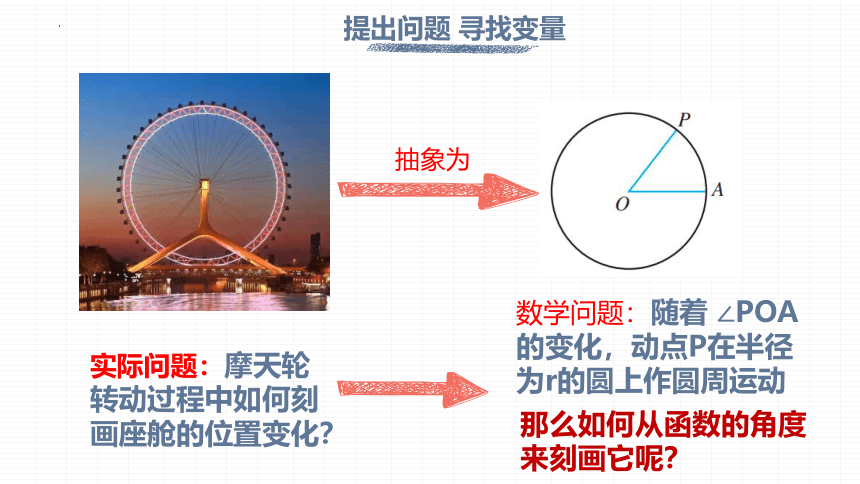
实际问题:摩天轮转动过程中如何刻画座舱的位置变化?
提出问题 寻找变量
数学问题:随着 POA的变化,动点P在半径为r的圆上作圆周运动
抽象为
那么如何从函数的角度来刻画它呢?
今天我们继续按照研究函数的一般套路来展开探究。
我们知道,函数是描述客观世界运动变化规律的数学模型。
如:直线运动-----一次函数;抛物运动-----二次函数;
指数爆炸-----指数函数;对数增长-----对数函数;
那么圆周运动-----用什么函数模型刻画呢?
提出问题,引导探索
函数问题的研究路径:
背景-定义-图象-性质-应用
在弧度制下,我们已经把角的范围扩展到全体实数.
引导探索,形成概念
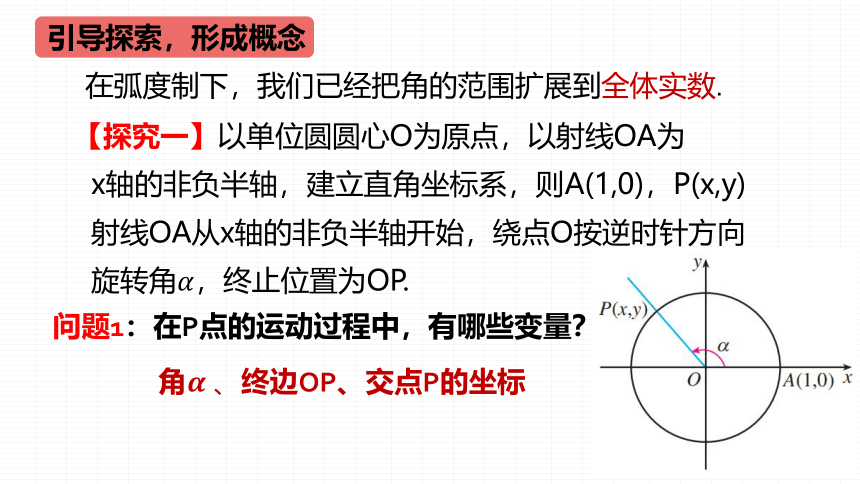
【探究一】以单位圆圆心O为原点,以射线OA为
x轴的非负半轴,建立直角坐标系,则A(1,0),P(x,y)
射线OA从x轴的非负半轴开始,绕点O按逆时针方向
旋转角,终止位置为OP.
问题1:在P点的运动过程中,有哪些变量?
角终边OP、交点P的坐标
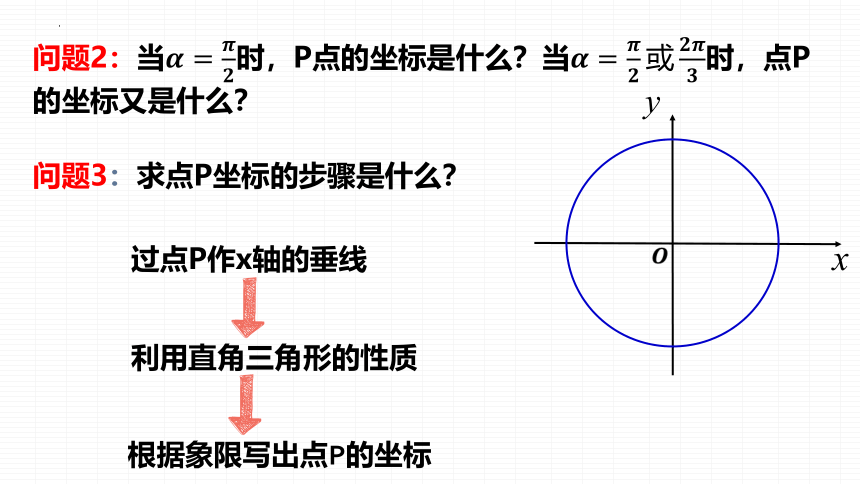
问题2:当时,P点的坐标是什么?当时,点P的坐标又是什么?
问题3:求点P坐标的步骤是什么?
过点P作x轴的垂线
利用直角三角形的性质
根据象限写出点P的坐标
问题4:任意给定一个角, 终边与单位圆的交点P的坐标唯一确定吗?那么能否运用函数的语言刻画这种对应关系呢?
这里有两个对应关系:
:实数(弧度)对应于点P的纵坐标y ①
:实数(弧度)对应于点P的横坐标x ②
所以,点P的横坐标x,纵坐标y都是角函数。
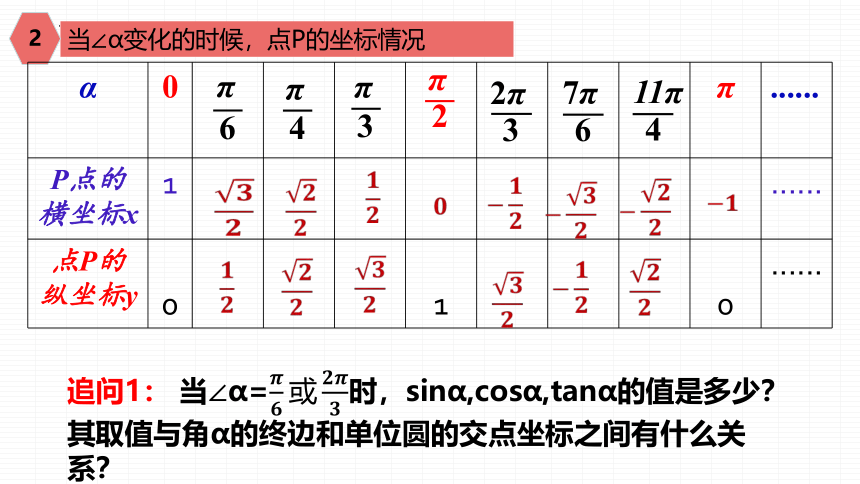
当∠α变化的时候,点P的坐标情况
2
α 0 π ......
P点的横坐标x 1 ......
点P的纵坐标y 0 1 0 ......
π
6
π
4
π
3
2π
3
7π
6
11π
4
π
2
追问1: 当∠α=时,sinα,cosα,tanα的值是多少?其取值与角α的终边和单位圆的交点坐标之间有什么关系?
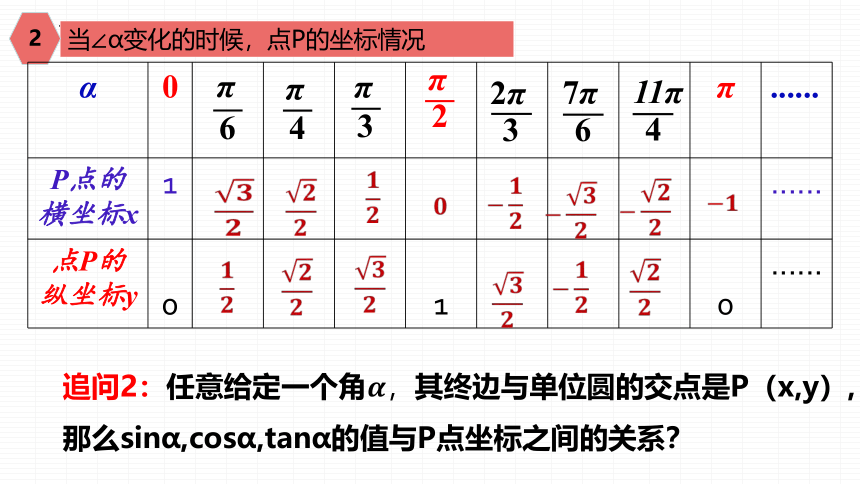
当∠α变化的时候,点P的坐标情况
2
α 0 π ......
P点的横坐标x 1 ......
点P的纵坐标y 0 1 0 ......
π
6
π
4
π
3
2π
3
7π
6
11π
4
π
2
追问2:任意给定一个角其终边与单位圆的交点是P(x,y),那么sinα,cosα,tanα的值与P点坐标之间的关系?
设α是一个任意角,α∈R,它的终边与单位圆相交于点P(x,y)
(1)y叫做α的正弦函数,记作sinα,即y=sinα;
(2)x叫做α的余弦函数,记作cosα,即x=cosα;
(3) 叫做α的正切,记作tanα,即
引导探索,形成概念
我们把正弦函数、余弦函数和正切函数统称为三角函数.
习惯上,我们用x表示自变量,y表示因变量,通常它们记为:
正弦函数:
余弦函数:
正切函数:
概念辨析
追问:任意角的三角函数的定义域分别是什么呢?
对任意角,正弦值、余弦值总有意义
当的终边在y轴上时,点P 的横坐标等于0,
无意义,此时
初中定义 高中定义
联系
函数值符号
值均为正数
可正可负可零
角的范围
锐角
任意角
高中三角函数的定义统一和兼容了初中三角函数的定义
函数值定义
边长比值
终边上点的坐标
?
?
?
?
?
?
?
问题5:初中也有三角函数,那初高中的定义有什么区别和联系
例1:利用三角函数的定义求 的正弦、余弦和正切值。
知识应用 合作交流
算比值(对正切函数)
画终边
找交点坐标
追问:三个三角函数值
请说出角值。
问题8: 如果改变角α终边上点P的位置,三角函数值是否会改变呢?
知识应用 合作交流
例2:如图,∠α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r;
求证:
证明:
设∠α的终边与单位圆交于点P0(x0,y0),分别过点P,P0作x轴的垂线PM,P0M0,垂足分别为M,M0,则:
α
例2:如图,∠α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r;
求证:
证明:
由此可知,只要知道∠α终边上任意一点P的坐标,就可以求得∠α的三个三角函数值。
α
终边上任一点三角函数定义:
归纳
知识应用 合作交流
小结:当点的坐标
含有参数时,
应分类讨论.
周期现象
单位圆上的圆周运动
特殊化
几何对应
三角函数
定义
表示
辨析
……
反思凝练,感悟升华
【课堂反馈 】
B
A
D
知识应用 合作交流
5.2.1三角函数的概念
引导语:在客观世界中存在大量循环往复、周而复始的周期现象,比如日出日落、钟摆运动等,匀速圆周运动是这类现象的代表
实际问题:摩天轮转动过程中如何刻画座舱的位置变化?
提出问题 寻找变量
数学问题:随着 POA的变化,动点P在半径为r的圆上作圆周运动
抽象为
那么如何从函数的角度来刻画它呢?
今天我们继续按照研究函数的一般套路来展开探究。
我们知道,函数是描述客观世界运动变化规律的数学模型。
如:直线运动-----一次函数;抛物运动-----二次函数;
指数爆炸-----指数函数;对数增长-----对数函数;
那么圆周运动-----用什么函数模型刻画呢?
提出问题,引导探索
函数问题的研究路径:
背景-定义-图象-性质-应用
在弧度制下,我们已经把角的范围扩展到全体实数.
引导探索,形成概念
【探究一】以单位圆圆心O为原点,以射线OA为
x轴的非负半轴,建立直角坐标系,则A(1,0),P(x,y)
射线OA从x轴的非负半轴开始,绕点O按逆时针方向
旋转角,终止位置为OP.
问题1:在P点的运动过程中,有哪些变量?
角终边OP、交点P的坐标
问题2:当时,P点的坐标是什么?当时,点P的坐标又是什么?
问题3:求点P坐标的步骤是什么?
过点P作x轴的垂线
利用直角三角形的性质
根据象限写出点P的坐标
问题4:任意给定一个角, 终边与单位圆的交点P的坐标唯一确定吗?那么能否运用函数的语言刻画这种对应关系呢?
这里有两个对应关系:
:实数(弧度)对应于点P的纵坐标y ①
:实数(弧度)对应于点P的横坐标x ②
所以,点P的横坐标x,纵坐标y都是角函数。
当∠α变化的时候,点P的坐标情况
2
α 0 π ......
P点的横坐标x 1 ......
点P的纵坐标y 0 1 0 ......
π
6
π
4
π
3
2π
3
7π
6
11π
4
π
2
追问1: 当∠α=时,sinα,cosα,tanα的值是多少?其取值与角α的终边和单位圆的交点坐标之间有什么关系?
当∠α变化的时候,点P的坐标情况
2
α 0 π ......
P点的横坐标x 1 ......
点P的纵坐标y 0 1 0 ......
π
6
π
4
π
3
2π
3
7π
6
11π
4
π
2
追问2:任意给定一个角其终边与单位圆的交点是P(x,y),那么sinα,cosα,tanα的值与P点坐标之间的关系?
设α是一个任意角,α∈R,它的终边与单位圆相交于点P(x,y)
(1)y叫做α的正弦函数,记作sinα,即y=sinα;
(2)x叫做α的余弦函数,记作cosα,即x=cosα;
(3) 叫做α的正切,记作tanα,即
引导探索,形成概念
我们把正弦函数、余弦函数和正切函数统称为三角函数.
习惯上,我们用x表示自变量,y表示因变量,通常它们记为:
正弦函数:
余弦函数:
正切函数:
概念辨析
追问:任意角的三角函数的定义域分别是什么呢?
对任意角,正弦值、余弦值总有意义
当的终边在y轴上时,点P 的横坐标等于0,
无意义,此时
初中定义 高中定义
联系
函数值符号
值均为正数
可正可负可零
角的范围
锐角
任意角
高中三角函数的定义统一和兼容了初中三角函数的定义
函数值定义
边长比值
终边上点的坐标
?
?
?
?
?
?
?
问题5:初中也有三角函数,那初高中的定义有什么区别和联系
例1:利用三角函数的定义求 的正弦、余弦和正切值。
知识应用 合作交流
算比值(对正切函数)
画终边
找交点坐标
追问:三个三角函数值
请说出角值。
问题8: 如果改变角α终边上点P的位置,三角函数值是否会改变呢?
知识应用 合作交流
例2:如图,∠α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r;
求证:
证明:
设∠α的终边与单位圆交于点P0(x0,y0),分别过点P,P0作x轴的垂线PM,P0M0,垂足分别为M,M0,则:
α
例2:如图,∠α是一个任意角,它的终边上任意一点P(不与原点O重合)的坐标为(x,y),点P与原点的距离为r;
求证:
证明:
由此可知,只要知道∠α终边上任意一点P的坐标,就可以求得∠α的三个三角函数值。
α
终边上任一点三角函数定义:
归纳
知识应用 合作交流
小结:当点的坐标
含有参数时,
应分类讨论.
周期现象
单位圆上的圆周运动
特殊化
几何对应
三角函数
定义
表示
辨析
……
反思凝练,感悟升华
【课堂反馈 】
B
A
D
知识应用 合作交流
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
