平面的基本性质和推论(辽宁省大连市)
文档属性
| 名称 | 平面的基本性质和推论(辽宁省大连市) |

|
|
| 格式 | rar | ||
| 文件大小 | 321.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-04 12:53:00 | ||
图片预览




文档简介
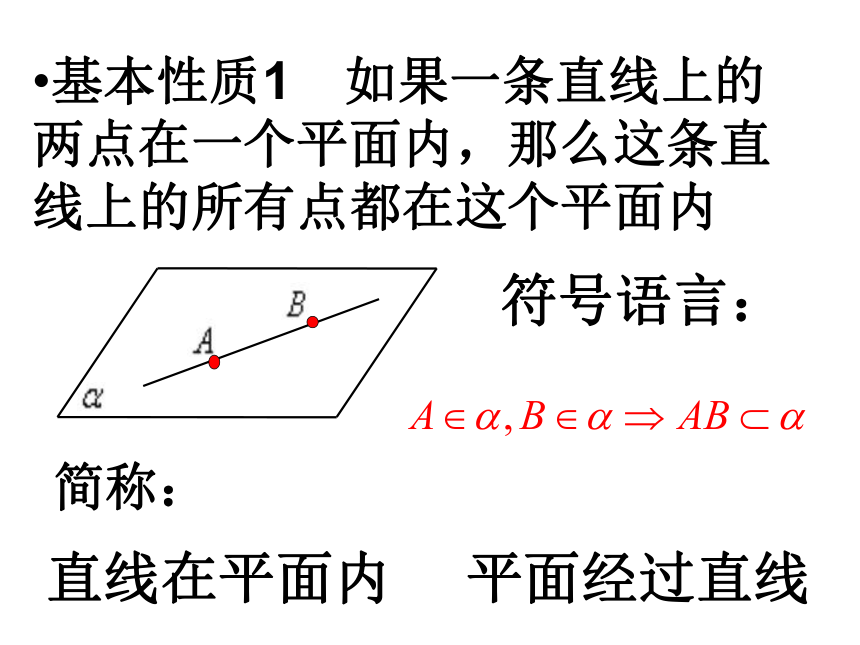
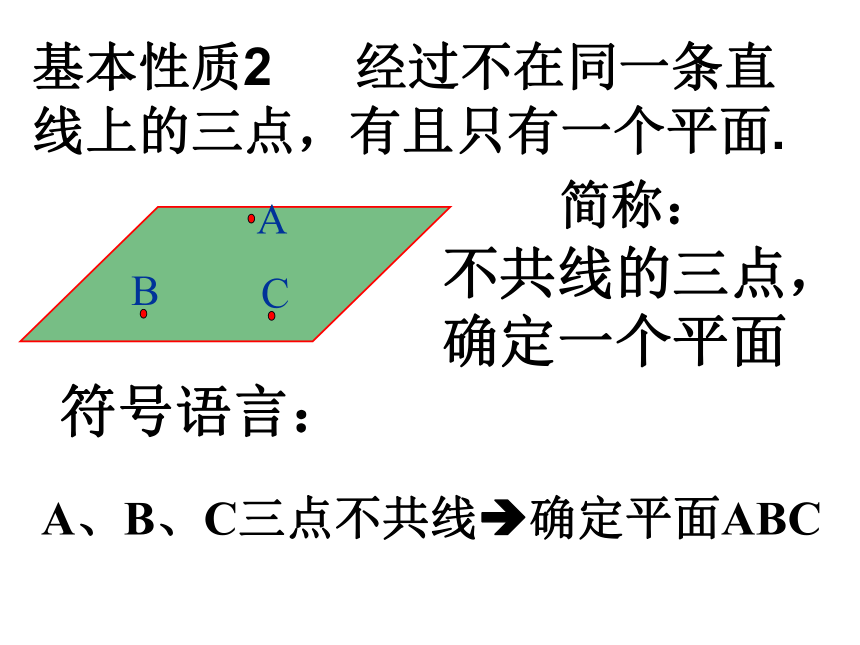
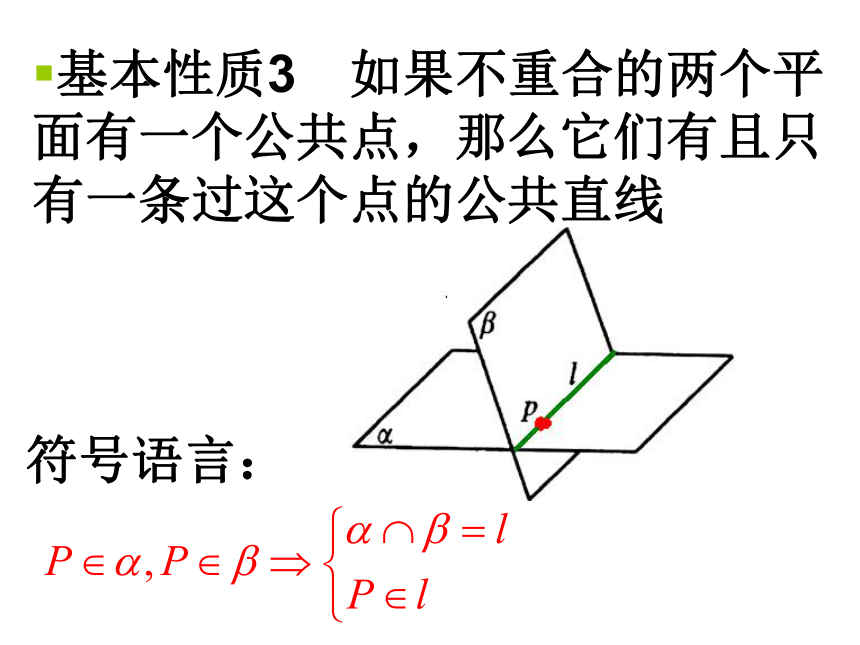
课件14张PPT。1.2.1平面的基本性质和推论平面的基本性质1.连接两点的线中,线段最短2.过两点有一条直线,并且只有一条线段点和直线的性质:基本性质1 如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内符号语言:直线在平面内平面经过直线简称:反之,若一条直线 l 在平面α内,则直线上 的所有点均在此平面α内基本性质1应用:(1)证明直线在平面内.(2)证明点在平面内;基本性质2 经过不在同一条直线上的三点,有且只有一个平面. A、B、C三点不共线?确定平面ABC符号语言:简称:不共线的三点,确定一个平面基本性质2应用:(1)确定平面的依据;(2)证明有关点、线共面.基本性质3 如果不重合的两个平面有一个公共点,那么它们有且只有一条过这个点的公共直线符号语言:(1)判定两个平面的相交;(2)证明点在直线上
(如证三线共点或三点共线);基本性质3应用:两个相交平面的常见画法:α?aα?a平卧式竖式推论1: 简称:直线和直线外一点确定一个平面 推论1: 经过一条直线和这条直线外的一点,有且只有一个平面 求证:过点A和直线a可以确定一个平面 所以经过点A和直线a有且只有一个平面 唯一性: 如果经过点A和直线a的平面还有一个平面β,那么A∈β, B ∈ β,C ∈ β因为A∈α, B∈α,C∈α, (公理1)故不共线的三点A,B,C既在平面α内又在平面β内.所以平面α和平面β重合.(公理3)推论2: 经过两条相交直线,有且只有一 个平面。简称:两条相交直线确定一个平面 推论3:经过两条平行直线有且只有一个平面。简称:两条平行直线确定一个平面平面的基本性质性质1: 如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内。性质3:如果不重合两个平面有一个公共点,那么它们有且只有一条经过这个点的公共直线推论1:经过一条直线和这条直线外的一点,有且只有一个平面。推论2: 经过两条相交直线,有且只有一个平面。 推论3:经过两条平行直线有,且只有一个平面。基本题型证明三线共点:先确定两条直线交点,再证交点在第三条直线上。证明点共线:证明这些点同时在两相交平面内证明点共面或线共面:先由一些元素确定一个平面,再证另一些元素也在这个平面内。性质2:经过不在同一条直线上的三点,有且只有一个平面。
(如证三线共点或三点共线);基本性质3应用:两个相交平面的常见画法:α?aα?a平卧式竖式推论1: 简称:直线和直线外一点确定一个平面 推论1: 经过一条直线和这条直线外的一点,有且只有一个平面 求证:过点A和直线a可以确定一个平面 所以经过点A和直线a有且只有一个平面 唯一性: 如果经过点A和直线a的平面还有一个平面β,那么A∈β, B ∈ β,C ∈ β因为A∈α, B∈α,C∈α, (公理1)故不共线的三点A,B,C既在平面α内又在平面β内.所以平面α和平面β重合.(公理3)推论2: 经过两条相交直线,有且只有一 个平面。简称:两条相交直线确定一个平面 推论3:经过两条平行直线有且只有一个平面。简称:两条平行直线确定一个平面平面的基本性质性质1: 如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内。性质3:如果不重合两个平面有一个公共点,那么它们有且只有一条经过这个点的公共直线推论1:经过一条直线和这条直线外的一点,有且只有一个平面。推论2: 经过两条相交直线,有且只有一个平面。 推论3:经过两条平行直线有,且只有一个平面。基本题型证明三线共点:先确定两条直线交点,再证交点在第三条直线上。证明点共线:证明这些点同时在两相交平面内证明点共面或线共面:先由一些元素确定一个平面,再证另一些元素也在这个平面内。性质2:经过不在同一条直线上的三点,有且只有一个平面。
