2023-2024学年河南省南阳市邓州市八年级(上)期中数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年河南省南阳市邓州市八年级(上)期中数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 88.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 21:31:55 | ||
图片预览



文档简介
2023-2024学年河南省南阳市邓州市八年级(上)期中数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.实数的平方根是( )
A. B. C. D.
2.下列各数的立方根是的数是( )
A. B. C. D.
3.在九章算术一书中,对开方开不尽的数起了一个名字,叫做“面”,这是中国传统数学对无理数的最早记载下面符合“面”的描述的数是( )
A. B. C. D.
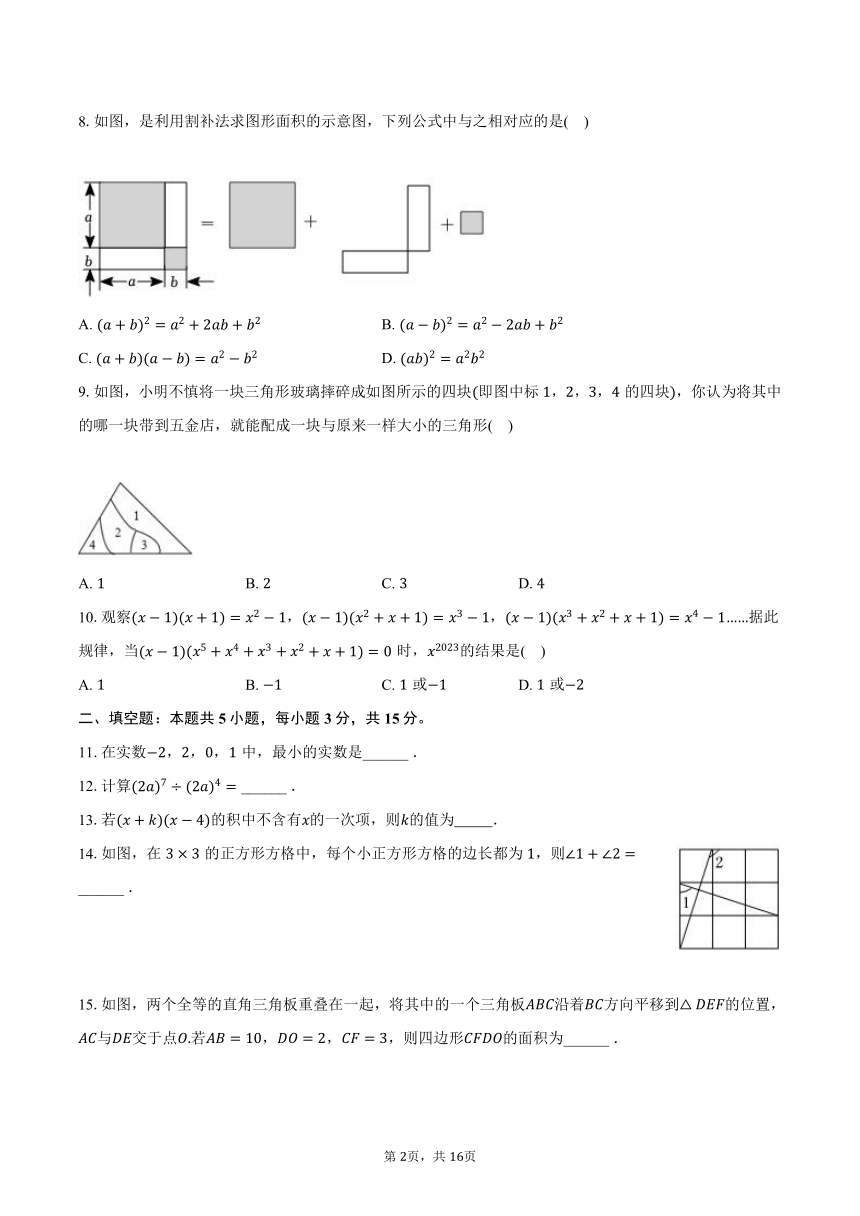
4.下列运算正确的是( )
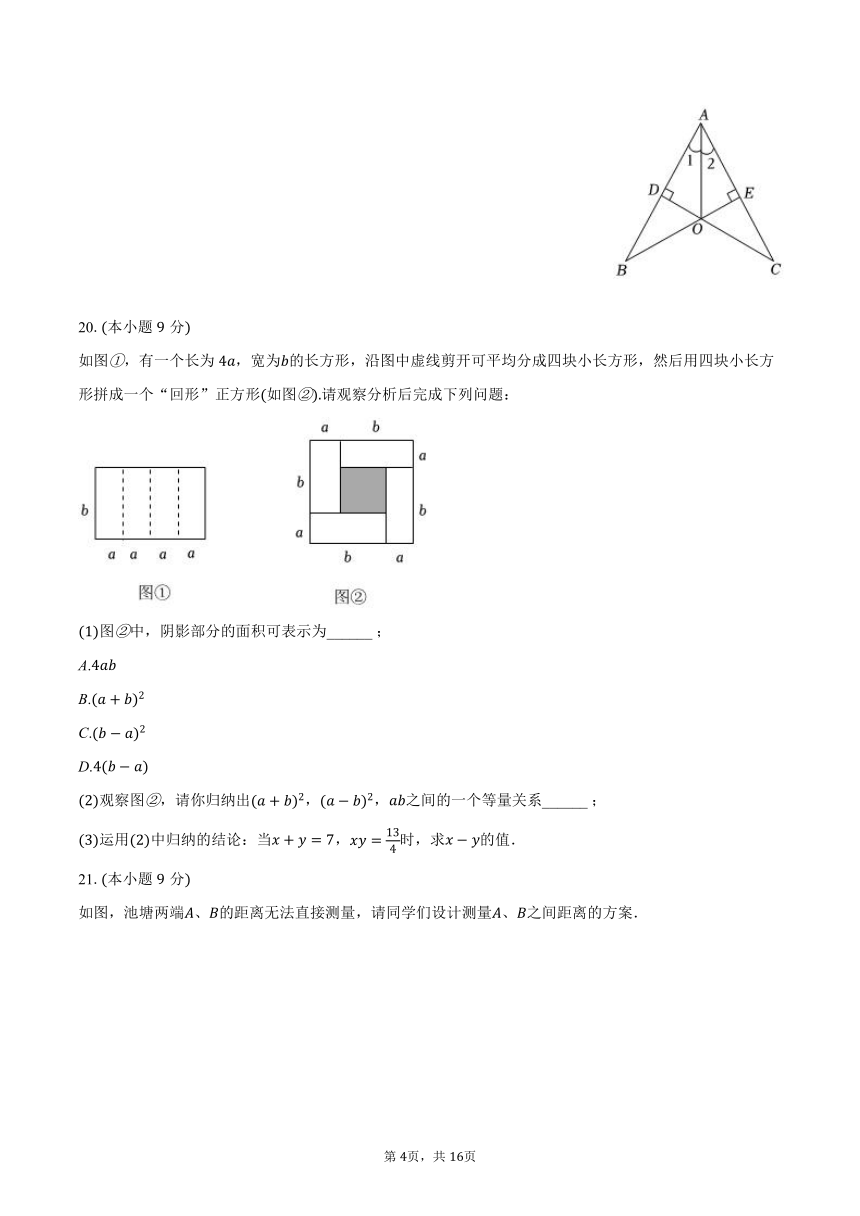
A. B. C. D.
5.在电子显微镜下测得一个圆球体细胞的直径是纳米,则个这样的细胞排成的细胞链的长是( )
A. 纳米 B. 纳米 C. 纳米 D. 纳米
6.计算:的结果是( )
A. B. C. D.
7.如图,旋转得到,则下列结论不成立的是( )
A. 点与点是对应点 B.
C. D.
8.如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是( )
A. B.
C. D.
9.如图,小明不慎将一块三角形玻璃摔碎成如图所示的四块即图中标,,,的四块,你认为将其中的哪一块带到五金店,就能配成一块与原来一样大小的三角形( )
A. B. C. D.
10.观察,,据此规律,当时,的结果是( )
A. B. C. 或 D. 或
二、填空题:本题共5小题,每小题3分,共15分。
11.在实数,,,中,最小的实数是______ .
12.计算 ______ .
13.若的积中不含有的一次项,则的值为 .
14.如图,在的正方形方格中,每个小正方形方格的边长都为,则 ______ .
15.如图,两个全等的直角三角板重叠在一起,将其中的一个三角板沿着方向平移到的位置,与交于点若,,,则四边形的面积为______ .
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:.
化简:.
17.本小题分
因式分解:
.
.
18.本小题分
发现任意五个连续整数的平方和是的倍数.
验证的结果是的几倍?
设五个连续整数的中间一个为,写出它们的平方和,并说明是的倍数.
19.本小题分
如图,点,分别在,上,,,相交于点,,求证:,小聪同学的证明过程如下:
证明:在和中,
≌依据:______
依据:______
任务:
小聪同学的证明过程中依据是______ ,依据是______ ;
按小聪同学的思路将证明过程补充完整;
图中共有______ 对全等三角形,它们是______ .
20.本小题分
如图,有一个长为,宽为的长方形,沿图中虚线剪开可平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形如图请观察分析后完成下列问题:
图中,阴影部分的面积可表示为______ ;
A.
B.
C.
D.
观察图,请你归纳出,,之间的一个等量关系______ ;
运用中归纳的结论:当,时,求的值.
21.本小题分
如图,池塘两端、的距离无法直接测量,请同学们设计测量、之间距离的方案.
小明设计的方案如图:他先在平地上选取一个可以直接到达、的点,然后连接和,接着分别延长和并且使,,最后连接,测出的长即可.
小红的方案如图:先确定直线,过点作的垂线,在上选取一个可以直接到达点的点,连接,在线段的延长线上找一点,使,测的长即可.
你认为以上两种方案可以吗?请说明理由.
22.本小题分
阅读材料;杨辉三角,又称贾宪三角,是二项式系数在三角形中的一种几何排列,西方人帕斯卡发现时,已比宋代杨辉要迟年如图,根据你观察的杨辉三角的排列规律,完成下列问题.
判断的展开式共有______ 项;写出的第三项的系数是______ ;
计算与猜想:
计算:;
猜想:的展开式中含项的系数是______ ;
运用:若今天是星期五,过天仍是星期五,那么再过天是星期______ .
23.本小题分
已知,是直线上的点,,作于点,且,连结、.
自主探究:如图,当点在线段上,点在点右侧时,与的数量关系为______ ,位置关系为______ ;
思考拓展:如图,当点在线段的延长线上,点在点的左侧时,中的结论还成立吗?请说明理由;
能力提升:当点在线段的延长线上,点在点的______ 侧时,中的两个结论依然成立,若此时,,则的长度为______ .
答案和解析
1.【答案】
【解析】解:的平方根是;
故选:.
根据平方根的性质:正数有两个平方根,它们互为相反数,计算.
本题主要考查了平方根,熟练掌握平方根的性质:正数有两个平方根,它们互为相反数,是解题关键.
2.【答案】
【解析】解:立方根是的数是.
故选D.
利用立方根定义计算即可得到结果.
此题考查了立方根,熟练掌握立方根的定义是解本题的关键.
3.【答案】
【解析】解:、是开方开不尽的数,符合题意;
B、,不符合题意;
C、,不符合题意;
D、,不符合题意.
故选:.
根据实数的分类及算术平方根的定义解答即可.
本题考查的是实数,熟知实数的分类及算术平方根的定义是解题的关键.
4.【答案】
【解析】【分析】
此题主要考查了同底数幂的乘法运算以及幂的乘方运算、合并同类项等知识,正确掌握运算法则是解题关键.
分别利用同底数幂的乘法运算法则以及幂的乘方运算、合并同类项法则判断得出答案.
【解答】
解:、,故此选项错误;
B、,故此选项错误;
C、,正确;
D、,故此选项错误.
故选:.
5.【答案】
【解析】解:纳米,
即个这样的细胞排成的细胞链的长是纳米.
故选:.
科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数;当原数的绝对值时,是负整数.
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
6.【答案】
【解析】解:
.
故选:.
先去括号,再合并同类项即可.
本题主要考查整式的除法,解答的关键是对相应的运算法则的掌握.
7.【答案】
【解析】解:根据旋转的性质可知,
点与点是对应点,
,
,
.
故选:.
旋转后,对应点与旋转中心共线,对应线段平行且相等,对应点到旋转中心的距离相等,对应角相等,其中与不是对应角,不能判断相等.
本题考查旋转的性质:旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.同时要注意旋转的三要素:定点旋转中心;旋转方向;旋转角度.
8.【答案】
【解析】【分析】
本题主要考查了完全平方公式的几何背景,熟练掌握完全平方公式的几何背景的计算方法进行求解是解决本题的关键.
左边大正方形的边长为,面积为,由边长为的正方形,个长为宽为的长方形,边长为的正方形组成,根据面积相等即可得出答案.
【解答】
解:根据题意,大正方形的边长为,面积为,
由边长为的正方形,个长为宽为的长方形,边长为的正方形组成,
所以.
故选:.
9.【答案】
【解析】解:、、块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第块有完整的两角及夹边,符合,满足题目要求的条件,是符合题意的.
故选:.
本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.
本题主要考查三角形全等的判定,看这块玻璃中哪个包含的条件符合某个判定.判定两个三角形全等的一般方法有:、、、、.
10.【答案】
【解析】解:,
,
,
,
,
,
解得或,
当时,;
当时,,
故选:.
先归纳出计算规律,再运用此规律求得的值,最后代入计算、求解.
此题考查了数式变化类规律问题的应用能力,关键是能准确归纳和运用规律进行正确地计算.
11.【答案】
【解析】解:,
最小的实数是,
故答案为:.
根据正数大于,大于负数比较即可得出结果.
本题考查了实数的大小比较,熟练掌握实数的大小比较方法是解题的关键.
12.【答案】
【解析】解:
,
故答案为:.
根据同底数幂相除,底数不变,指数相减;积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘计算即可.
本题考查了同底数幂的除法,积的乘方,熟练掌握这两个运算法则是解题的关键.
13.【答案】
【解析】解:,
的积中不含有的一次项,
,即.
故答案为:.
利用多项式乘以多项式法则计算得到结果,令一次项系数为即可求出的值.
此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.
14.【答案】
【解析】解:如图,
在与中,
,
≌,
.
,
.
故答案为:.
根据全等三角形的判定和性质定理即可得到结论.
本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.
15.【答案】
【解析】解:沿着方向平移到,
≌,
,,
,,
四边形的面积.
故答案为:.
根据全等三角形的性质得到,,根据梯形的面积公式计算,得到答案.
本题考查的是平移的性质、全等三角形的性质以及梯形的面积计算,掌握全等三角形的对应边相等是解题的关键.
16.【答案】解:
;
.
【解析】先算乘方,开方,再算加减即可;
先算完全平方,平方差,单项式乘多项式,再合并同类项即可.
本题主要考查整式的混合运算,解答的关键是对相应的运算法则的掌握.
17.【答案】解:原式;
原式
.
【解析】先提公因式,再利用平方差公式进行因式分解;
先根据乘法公式展开,再利用完全平方公式进行因式分解.
本题考查提公因式法、公式法因式分解,掌握平方差公式、完全平方公式的结构特征是正确应用的前提.
18.【答案】解:验证,,
即的结果是的倍;
五个连续整数的中间一个为,则其余的个整数
分别是,,,,
它们的平方和为:
,
,
又是整数,是整数,
五个连续整数的平方和是的倍数.
【解析】计算出算式的结果除以,即可解答;
设出五个连续整数的中间一个为,则其余的个整数分别是,,,,求出它们的平方和,利用因式分解,即可解答.
本题考查了因式分解的应用,解决本题的关键是求出平方和.
19.【答案】 全等三角形的对应边相等 全等三角形的对应边相等 四 ≌,≌,≌,≌
【解析】依据:,依据:全等三角形的对应边相等.
故答案为:,全等三角形的对应边相等;
证明:在和中,
,
≌,
全等三角形的对应边相等,
在和中,
,
≌,
;
图中共有四对全等三角形,它们是≌,≌,≌,≌.
故答案为:≌,≌,≌,≌.
依据是,依据是全等三角形的性质;
先证明≌,证得,然后证明≌证得结论;
图中共有四对全等三角形.
本题考查的是全等三角形的判定和性质,掌握三角形全等的判定定理是解题的关键.
20.【答案】
【解析】解:阴影部分正方形的边长为,
阴影部分的面积可表示为.
故答案为:.
图中阴影部分的面积既可表示为,即,又可表示为,
,
故答案为:.
根据中归纳的结论,得,
当,时,,
.
用和表示出阴影部分正方形的边长,进而表示出其面积;
分别用两种方法表示阴影部分正方形的面积:一种是中的表示方法,另一种是大正方形的面积减去个小长方形的面积,二者相等,从而得到,,之间的等量关系;
分别令,,代入中的结论,求出的值即可.
本题考查完全平方公式的几何背景,熟练掌握完全平方公式是解题的关键.
21.【答案】解:以上两种方案可以,理由如下:
甲同学方案:
在和中,
,
≌,
;
乙同学方案:
在和中,
,
≌,
.
【解析】分别证明≌,≌,即可解决问题.
本题考查了全等三角形的判定与性质,全等三角形的应用,解决本题的关键是得到≌和≌.
22.【答案】 六
【解析】解:
故答案为:,;
,
,
含项的系数为,
故答案为:;
,
再过天是星期六,
故答案为:六.
杨辉三角可得;
根据杨辉三角,化简求值,
展开可知含项的系数;
,展开,即可知再过天是星期几.
本题考查了杨辉三角,关键是掌握并运用杨辉三角.
23.【答案】 左
【解析】解:,,
,
在和中,
,
≌,
,,
,
,
,
,
故答案为:,;
中的结论还成立,理由如下:
,
,
同得:≌,
,,
,
,
即,
;
如图,当点在线段的延长线上,点在点的左侧时,中的两个结论依然成立,理由如下:
同得:≌,
,,,
,
,
即,
,
,,
,
,
故答案为:左,.
证≌,得,,再证,则;
同得≌,则,,再证,则;
同得:≌,得,,,再证,则,然后求出,得即可.
本题是三角形综合题,考查了全等三角形的判定与性质、垂直的定义以及直角三角形的性质等知识,本题综合性强,熟练掌握全等三角形的判定与性质是解题的关键,属于中考常考题型.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.实数的平方根是( )
A. B. C. D.
2.下列各数的立方根是的数是( )
A. B. C. D.
3.在九章算术一书中,对开方开不尽的数起了一个名字,叫做“面”,这是中国传统数学对无理数的最早记载下面符合“面”的描述的数是( )
A. B. C. D.
4.下列运算正确的是( )
A. B. C. D.
5.在电子显微镜下测得一个圆球体细胞的直径是纳米,则个这样的细胞排成的细胞链的长是( )
A. 纳米 B. 纳米 C. 纳米 D. 纳米
6.计算:的结果是( )
A. B. C. D.
7.如图,旋转得到,则下列结论不成立的是( )
A. 点与点是对应点 B.
C. D.
8.如图,是利用割补法求图形面积的示意图,下列公式中与之相对应的是( )
A. B.
C. D.
9.如图,小明不慎将一块三角形玻璃摔碎成如图所示的四块即图中标,,,的四块,你认为将其中的哪一块带到五金店,就能配成一块与原来一样大小的三角形( )
A. B. C. D.
10.观察,,据此规律,当时,的结果是( )
A. B. C. 或 D. 或
二、填空题:本题共5小题,每小题3分,共15分。
11.在实数,,,中,最小的实数是______ .
12.计算 ______ .
13.若的积中不含有的一次项,则的值为 .
14.如图,在的正方形方格中,每个小正方形方格的边长都为,则 ______ .
15.如图,两个全等的直角三角板重叠在一起,将其中的一个三角板沿着方向平移到的位置,与交于点若,,,则四边形的面积为______ .
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:.
化简:.
17.本小题分
因式分解:
.
.
18.本小题分
发现任意五个连续整数的平方和是的倍数.
验证的结果是的几倍?
设五个连续整数的中间一个为,写出它们的平方和,并说明是的倍数.
19.本小题分
如图,点,分别在,上,,,相交于点,,求证:,小聪同学的证明过程如下:
证明:在和中,
≌依据:______
依据:______
任务:
小聪同学的证明过程中依据是______ ,依据是______ ;
按小聪同学的思路将证明过程补充完整;
图中共有______ 对全等三角形,它们是______ .
20.本小题分
如图,有一个长为,宽为的长方形,沿图中虚线剪开可平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形如图请观察分析后完成下列问题:
图中,阴影部分的面积可表示为______ ;
A.
B.
C.
D.
观察图,请你归纳出,,之间的一个等量关系______ ;
运用中归纳的结论:当,时,求的值.
21.本小题分
如图,池塘两端、的距离无法直接测量,请同学们设计测量、之间距离的方案.
小明设计的方案如图:他先在平地上选取一个可以直接到达、的点,然后连接和,接着分别延长和并且使,,最后连接,测出的长即可.
小红的方案如图:先确定直线,过点作的垂线,在上选取一个可以直接到达点的点,连接,在线段的延长线上找一点,使,测的长即可.
你认为以上两种方案可以吗?请说明理由.
22.本小题分
阅读材料;杨辉三角,又称贾宪三角,是二项式系数在三角形中的一种几何排列,西方人帕斯卡发现时,已比宋代杨辉要迟年如图,根据你观察的杨辉三角的排列规律,完成下列问题.
判断的展开式共有______ 项;写出的第三项的系数是______ ;
计算与猜想:
计算:;
猜想:的展开式中含项的系数是______ ;
运用:若今天是星期五,过天仍是星期五,那么再过天是星期______ .
23.本小题分
已知,是直线上的点,,作于点,且,连结、.
自主探究:如图,当点在线段上,点在点右侧时,与的数量关系为______ ,位置关系为______ ;
思考拓展:如图,当点在线段的延长线上,点在点的左侧时,中的结论还成立吗?请说明理由;
能力提升:当点在线段的延长线上,点在点的______ 侧时,中的两个结论依然成立,若此时,,则的长度为______ .
答案和解析
1.【答案】
【解析】解:的平方根是;
故选:.
根据平方根的性质:正数有两个平方根,它们互为相反数,计算.
本题主要考查了平方根,熟练掌握平方根的性质:正数有两个平方根,它们互为相反数,是解题关键.
2.【答案】
【解析】解:立方根是的数是.
故选D.
利用立方根定义计算即可得到结果.
此题考查了立方根,熟练掌握立方根的定义是解本题的关键.
3.【答案】
【解析】解:、是开方开不尽的数,符合题意;
B、,不符合题意;
C、,不符合题意;
D、,不符合题意.
故选:.
根据实数的分类及算术平方根的定义解答即可.
本题考查的是实数,熟知实数的分类及算术平方根的定义是解题的关键.
4.【答案】
【解析】【分析】
此题主要考查了同底数幂的乘法运算以及幂的乘方运算、合并同类项等知识,正确掌握运算法则是解题关键.
分别利用同底数幂的乘法运算法则以及幂的乘方运算、合并同类项法则判断得出答案.
【解答】
解:、,故此选项错误;
B、,故此选项错误;
C、,正确;
D、,故此选项错误.
故选:.
5.【答案】
【解析】解:纳米,
即个这样的细胞排成的细胞链的长是纳米.
故选:.
科学记数法的表示形式为的形式,其中,为整数.确定的值时,要看把原数变成时,小数点移动了多少位,的绝对值与小数点移动的位数相同.当原数绝对值时,是正整数;当原数的绝对值时,是负整数.
此题考查科学记数法的表示方法.科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
6.【答案】
【解析】解:
.
故选:.
先去括号,再合并同类项即可.
本题主要考查整式的除法,解答的关键是对相应的运算法则的掌握.
7.【答案】
【解析】解:根据旋转的性质可知,
点与点是对应点,
,
,
.
故选:.
旋转后,对应点与旋转中心共线,对应线段平行且相等,对应点到旋转中心的距离相等,对应角相等,其中与不是对应角,不能判断相等.
本题考查旋转的性质:旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.同时要注意旋转的三要素:定点旋转中心;旋转方向;旋转角度.
8.【答案】
【解析】【分析】
本题主要考查了完全平方公式的几何背景,熟练掌握完全平方公式的几何背景的计算方法进行求解是解决本题的关键.
左边大正方形的边长为,面积为,由边长为的正方形,个长为宽为的长方形,边长为的正方形组成,根据面积相等即可得出答案.
【解答】
解:根据题意,大正方形的边长为,面积为,
由边长为的正方形,个长为宽为的长方形,边长为的正方形组成,
所以.
故选:.
9.【答案】
【解析】解:、、块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第块有完整的两角及夹边,符合,满足题目要求的条件,是符合题意的.
故选:.
本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.
本题主要考查三角形全等的判定,看这块玻璃中哪个包含的条件符合某个判定.判定两个三角形全等的一般方法有:、、、、.
10.【答案】
【解析】解:,
,
,
,
,
,
解得或,
当时,;
当时,,
故选:.
先归纳出计算规律,再运用此规律求得的值,最后代入计算、求解.
此题考查了数式变化类规律问题的应用能力,关键是能准确归纳和运用规律进行正确地计算.
11.【答案】
【解析】解:,
最小的实数是,
故答案为:.
根据正数大于,大于负数比较即可得出结果.
本题考查了实数的大小比较,熟练掌握实数的大小比较方法是解题的关键.
12.【答案】
【解析】解:
,
故答案为:.
根据同底数幂相除,底数不变,指数相减;积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘计算即可.
本题考查了同底数幂的除法,积的乘方,熟练掌握这两个运算法则是解题的关键.
13.【答案】
【解析】解:,
的积中不含有的一次项,
,即.
故答案为:.
利用多项式乘以多项式法则计算得到结果,令一次项系数为即可求出的值.
此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.
14.【答案】
【解析】解:如图,
在与中,
,
≌,
.
,
.
故答案为:.
根据全等三角形的判定和性质定理即可得到结论.
本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.
15.【答案】
【解析】解:沿着方向平移到,
≌,
,,
,,
四边形的面积.
故答案为:.
根据全等三角形的性质得到,,根据梯形的面积公式计算,得到答案.
本题考查的是平移的性质、全等三角形的性质以及梯形的面积计算,掌握全等三角形的对应边相等是解题的关键.
16.【答案】解:
;
.
【解析】先算乘方,开方,再算加减即可;
先算完全平方,平方差,单项式乘多项式,再合并同类项即可.
本题主要考查整式的混合运算,解答的关键是对相应的运算法则的掌握.
17.【答案】解:原式;
原式
.
【解析】先提公因式,再利用平方差公式进行因式分解;
先根据乘法公式展开,再利用完全平方公式进行因式分解.
本题考查提公因式法、公式法因式分解,掌握平方差公式、完全平方公式的结构特征是正确应用的前提.
18.【答案】解:验证,,
即的结果是的倍;
五个连续整数的中间一个为,则其余的个整数
分别是,,,,
它们的平方和为:
,
,
又是整数,是整数,
五个连续整数的平方和是的倍数.
【解析】计算出算式的结果除以,即可解答;
设出五个连续整数的中间一个为,则其余的个整数分别是,,,,求出它们的平方和,利用因式分解,即可解答.
本题考查了因式分解的应用,解决本题的关键是求出平方和.
19.【答案】 全等三角形的对应边相等 全等三角形的对应边相等 四 ≌,≌,≌,≌
【解析】依据:,依据:全等三角形的对应边相等.
故答案为:,全等三角形的对应边相等;
证明:在和中,
,
≌,
全等三角形的对应边相等,
在和中,
,
≌,
;
图中共有四对全等三角形,它们是≌,≌,≌,≌.
故答案为:≌,≌,≌,≌.
依据是,依据是全等三角形的性质;
先证明≌,证得,然后证明≌证得结论;
图中共有四对全等三角形.
本题考查的是全等三角形的判定和性质,掌握三角形全等的判定定理是解题的关键.
20.【答案】
【解析】解:阴影部分正方形的边长为,
阴影部分的面积可表示为.
故答案为:.
图中阴影部分的面积既可表示为,即,又可表示为,
,
故答案为:.
根据中归纳的结论,得,
当,时,,
.
用和表示出阴影部分正方形的边长,进而表示出其面积;
分别用两种方法表示阴影部分正方形的面积:一种是中的表示方法,另一种是大正方形的面积减去个小长方形的面积,二者相等,从而得到,,之间的等量关系;
分别令,,代入中的结论,求出的值即可.
本题考查完全平方公式的几何背景,熟练掌握完全平方公式是解题的关键.
21.【答案】解:以上两种方案可以,理由如下:
甲同学方案:
在和中,
,
≌,
;
乙同学方案:
在和中,
,
≌,
.
【解析】分别证明≌,≌,即可解决问题.
本题考查了全等三角形的判定与性质,全等三角形的应用,解决本题的关键是得到≌和≌.
22.【答案】 六
【解析】解:
故答案为:,;
,
,
含项的系数为,
故答案为:;
,
再过天是星期六,
故答案为:六.
杨辉三角可得;
根据杨辉三角,化简求值,
展开可知含项的系数;
,展开,即可知再过天是星期几.
本题考查了杨辉三角,关键是掌握并运用杨辉三角.
23.【答案】 左
【解析】解:,,
,
在和中,
,
≌,
,,
,
,
,
,
故答案为:,;
中的结论还成立,理由如下:
,
,
同得:≌,
,,
,
,
即,
;
如图,当点在线段的延长线上,点在点的左侧时,中的两个结论依然成立,理由如下:
同得:≌,
,,,
,
,
即,
,
,,
,
,
故答案为:左,.
证≌,得,,再证,则;
同得≌,则,,再证,则;
同得:≌,得,,,再证,则,然后求出,得即可.
本题是三角形综合题,考查了全等三角形的判定与性质、垂直的定义以及直角三角形的性质等知识,本题综合性强,熟练掌握全等三角形的判定与性质是解题的关键,属于中考常考题型.
第1页,共1页
同课章节目录
