方程的根与函数的零点

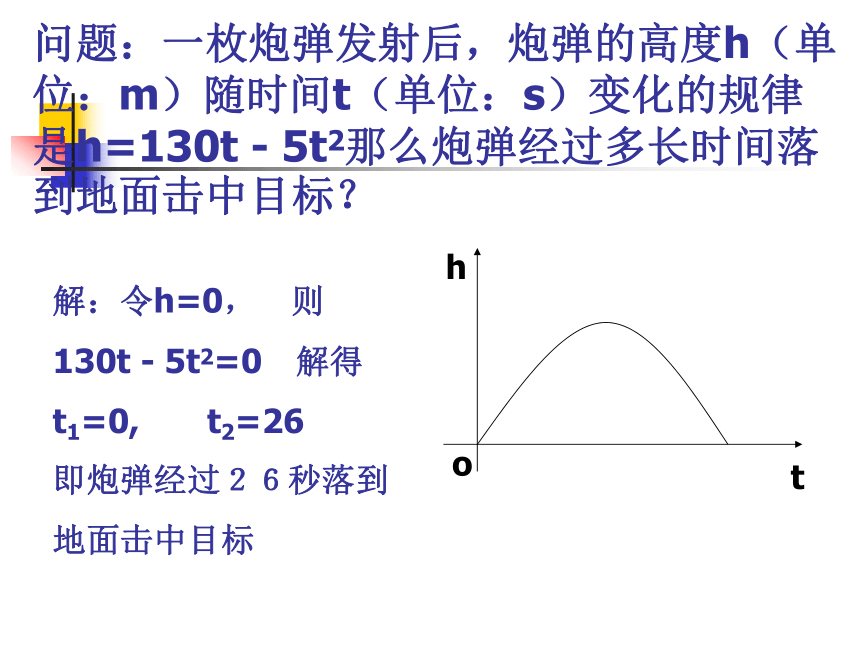
课件13张PPT。问题：一枚炮弹发射后，炮弹的高度h（单位：m）随时间t（单位：s）变化的规律是h=130t - 5t2那么炮弹经过多长时间落到地面击中目标？解：令h=0，　则
130t - 5t2=0　解得
t1=0,　　t2=26
即炮弹经过２６秒落到
地面击中目标
探究一:二次函数与对应的一元二次方程之间的关系(2)方程X2－2X +1=0与函数Y=X2 －2X +1
(3)方程X2－2X +3=0与函数Y=X2 －2X + 3思考1:观察函数图象上的一些特殊点的坐标及对
应二次方程的根,有什么发现?思考2 :一元二次方程根的个数及其判别式与对应
二次函数图象的位置有什么关系?研究:下面两组有类似的结论吗?合作探究进一步思考:二次函数与一元二次方程关系的应用例1.求证:一元二次方程2x2+3x-7=0有两个不 相 等
的实数根证法1:利用判别式证法2:取特殊点验证x轴下方有图象进一步判断
图象与x轴有两个交点思考:在上述证法中x的值是不是只有一 种取法呢?二次函数零点的概念推广得到:
对于函数 y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点(zero point)函数的零点与对应方程的关系例2:求下列函数的零点.反思小结：１．一元二次方程的解与相应的二次函数图象与轴的交点有什么关系？
２．函数零点是怎样定义的？
３．函数的零点与方程的根有什么关系？布置作业：谢谢指导！结论: