解直角三角形复习
图片预览



文档简介
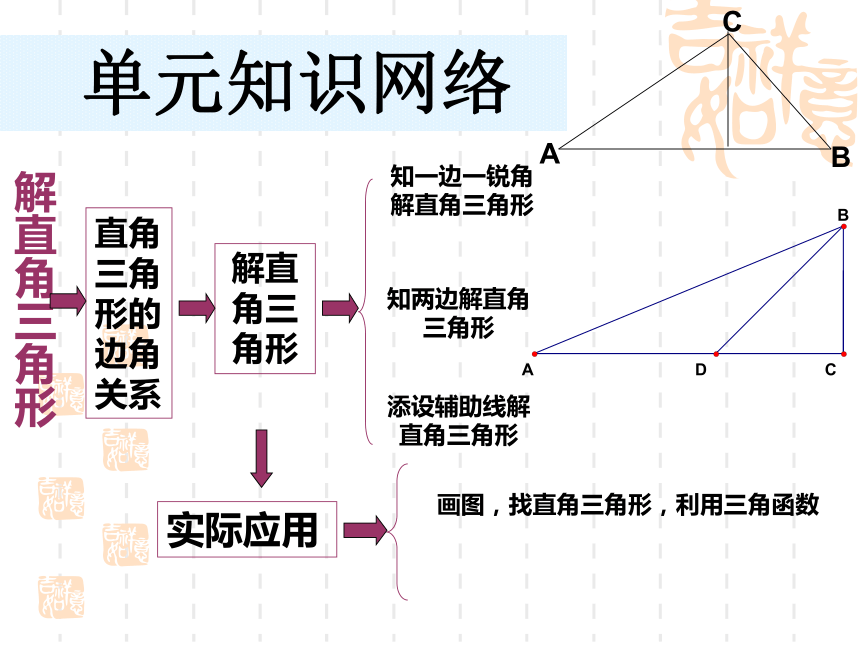
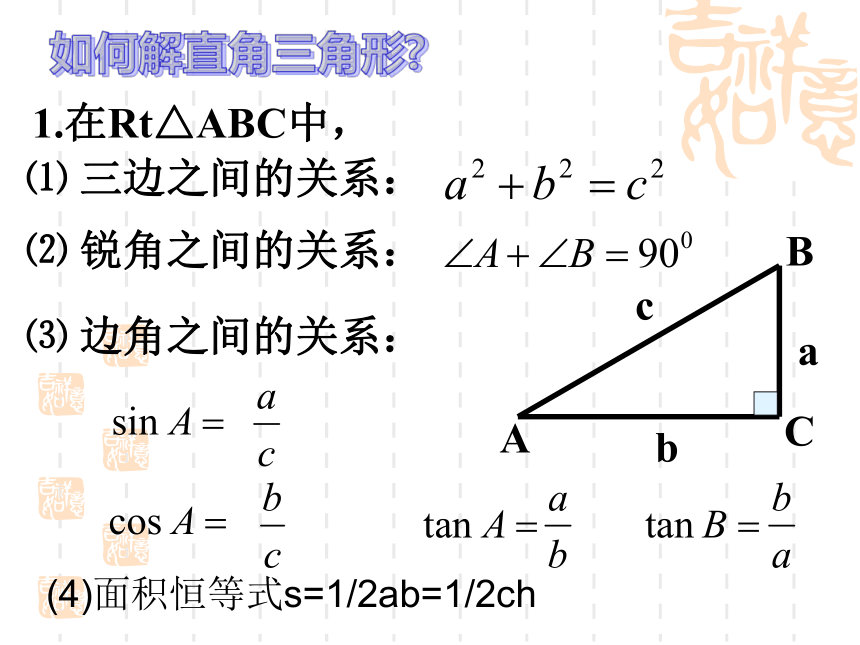
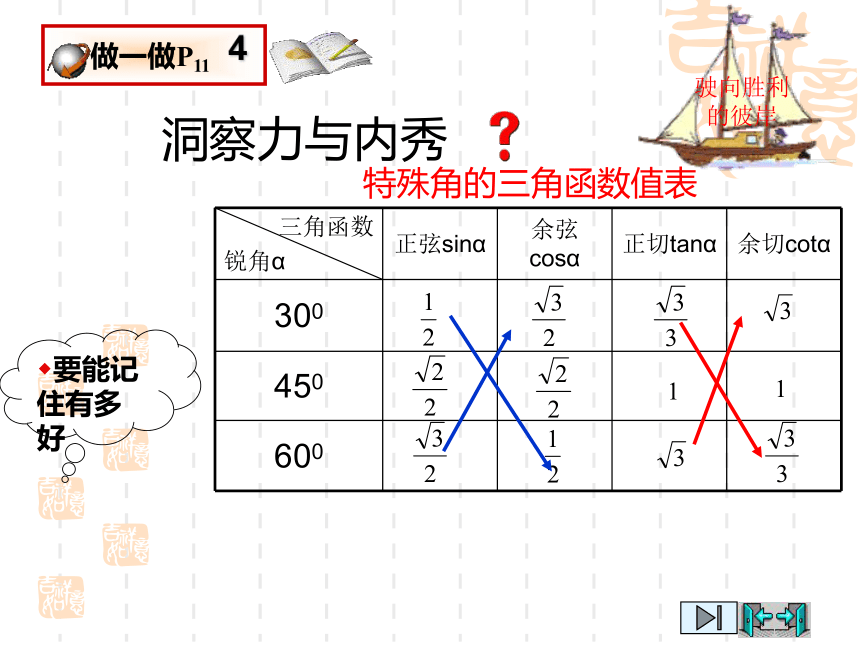
课件30张PPT。解直角三角形复习 单元知识网络直角三角形的边角关系解直 角三角形知一边一锐角解直角三角形知两边解直角三角形添设辅助线解直角三角形实际应用画图,找直角三角形,利用三角函数解直角三角形如何解直角三角形?1.在Rt△ABC中, ⑴ 三边之间的关系:⑵ 锐角之间的关系:⑶ 边角之间的关系:(4)面积恒等式s=1/2ab=1/2ch洞察力与内秀特殊角的三角函数值表要能记住有多好2.四个锐角三角函数的取值范围4.同角锐角三角函数之间的关系0000sin2α + cos2α = 1 tanα ? cotα = 15.互余两角三角函数之间的关系 sinA = cos(90o-A) cosA = sin(90o-A)
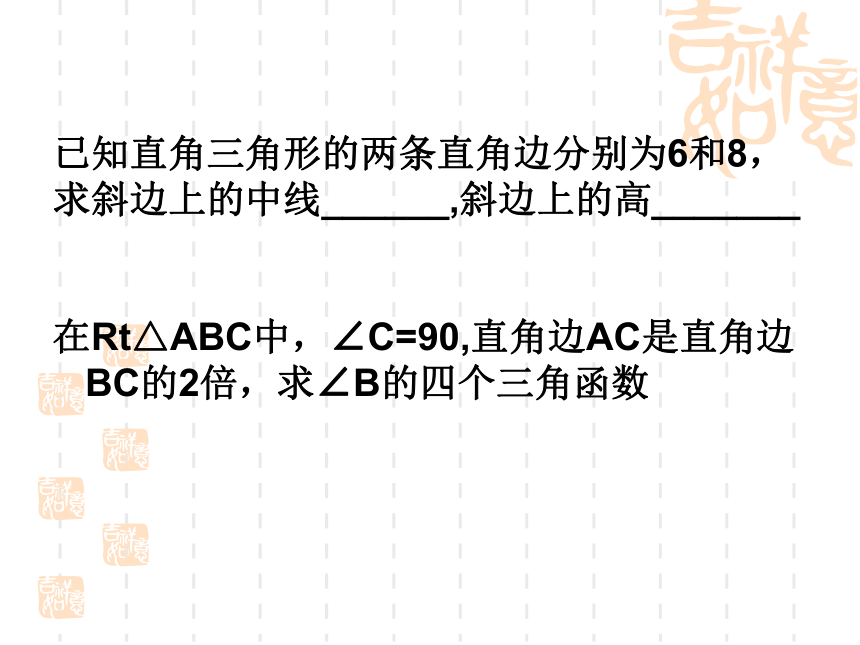
tanA = cot(90o-A) cotA = tan(90o-A) 三角函数应用三角函数是两边的比值,可以利用三角函数求边求角列关系式(列方程)已知直角三角形的两条直角边分别为6和8,
求斜边上的中线______,斜边上的高_______
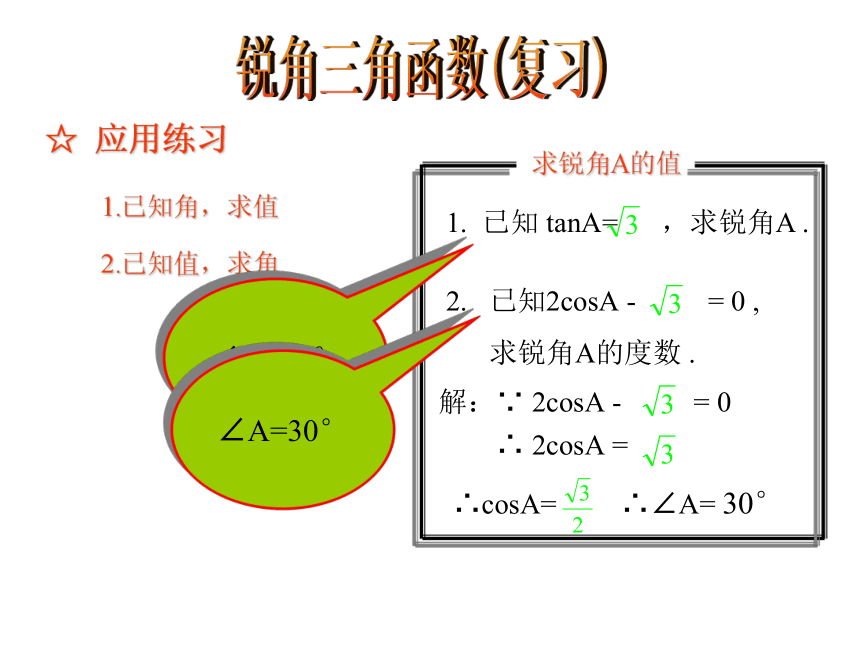
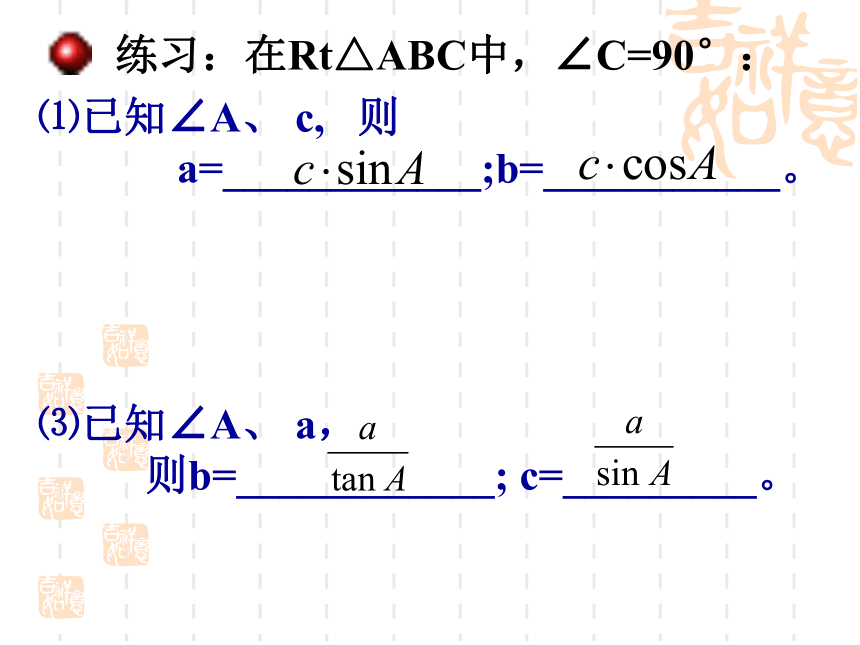
在Rt△ABC中,∠C=90,直角边AC是直角边BC的2倍,求∠B的四个三角函数锐角三角函数(复习)☆ 应用练习1.已知角,求值2.已知值,求角∠A=60°∠A=30°练习:在Rt△ABC中,∠C=90°:⑴已知∠A、 c, 则
a=____________;b=___________。⑶已知∠A、 a,
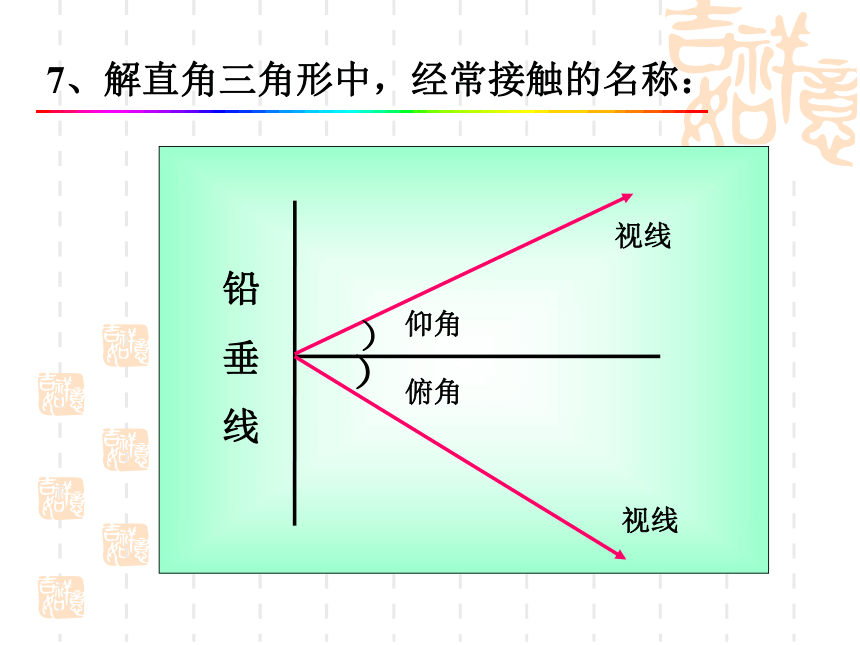
则b=____________; c=_________。7、解直角三角形中,经常接触的名称:铅
垂
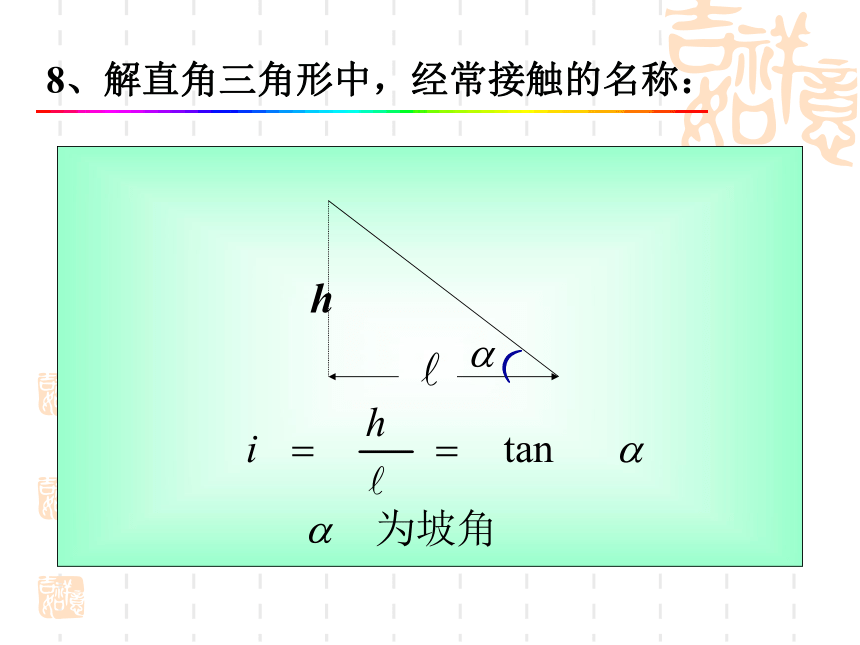
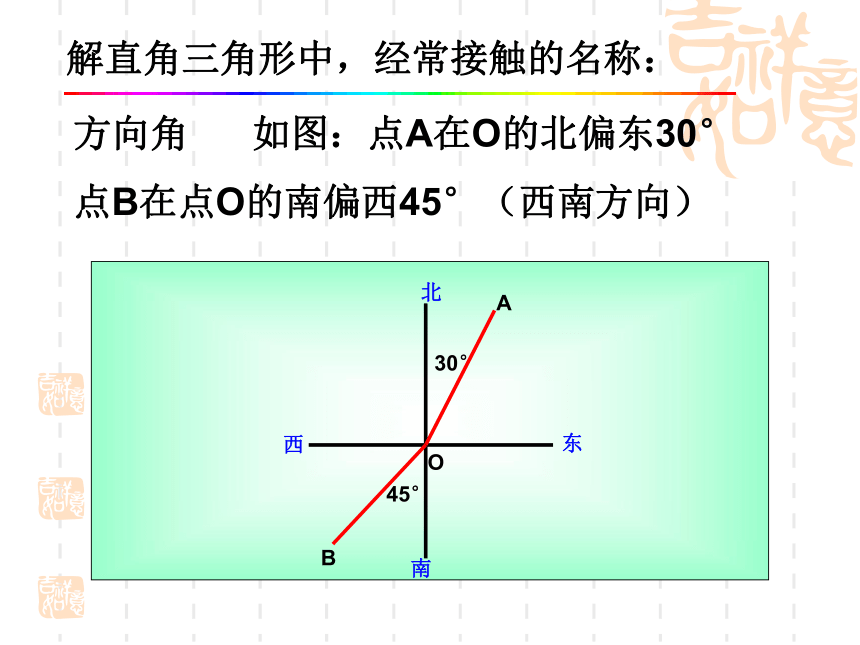
线视线视线仰角俯角))h8、解直角三角形中,经常接触的名称:)方向角 如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)解直角三角形中,经常接触的名称: 星期天,小华去图书超市购书,他乘电梯上楼,已知电梯AB段的长度8 m,倾斜角为300,则二楼的高度BC段是________mABC30048问题一D问题三:双直角三角形 在山脚A处测得山顶B的仰角为45°. 沿着水平地面向前300m到达D点,在D点测得山顶B的仰角为60 0,求山高BC.如图,在地面A点测得山顶上铁塔BD的塔顶和塔底的仰角分别是α= 600, β= 450,已知塔高BD=100m,求山高CD.ABCDαβ变式1 如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度.问题四:变式2变式3 已知铁塔塔基距楼房基水平距离BD为50米,由楼顶A望塔顶的仰角为45 o,由楼顶望塔底的俯角为30o,塔高DC为 ( )米D问题1楼房AB的高度是多少?问题2楼房CD的高度是多少?变式4 已知堤坝的横断面是梯形ABCD,上底CD 的宽为4,,坝高为4,坡角∠A=60°,坡角∠B=45°,求下底AB 的宽.变式5FE如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=8m,BC=5m,请你帮助计算一下这块花圃的面积?D30085变式611、如图,已知在Rt△ABC中,∠ACB=90度, CD是中线,P是CD上一点(P与C,D可以重合),BC=5,AC=12.
(1)若设CP=x,S△ACP=y,写出y与x 之间的函数关系式,并指出x的取值范围。
(2)求当y=10时,cot∠PAC的值。ACBDP练4.求tan15 °, tan22.5 °, tan75 ° 思 考在Rt△ABC中,∠C=90°斜边AB=2,直角边AC=1,∠ABC=30°,延长CB到D,连接AD使∠D=15°求tan15°的值。DACB北AC52° 22°B东东68°解:依题意得 ∠CBD=22°∠ABD=52°-22°=30°
∠BCA=22°+68°=90°
∵BC=2×30=60(海里)
∴AC=BC·sin30°=60×1/2=30(海里)
答:A、C的距离是30海里。
D练1.一船在海上B处以每小时30海里的速度,沿南偏东220方向航行,同时在B 处测得灯塔A 在南偏东520的方向上,航行2小时后到达C处,又测得灯塔A在北偏东680方向上,求A、C的距离。练2.(2000年广东中考题)在Rt△ABC中,E是斜边AB上的一点,把Rt△ABC沿CE折叠,点A与点B恰好重合,如果AC=4cm,求AB的长。解:由题意知:AC=BC
又:AC⊥BC
∴
∴
∴
即AB长为练3.如图,有一块直角三角形的纸片,两直角边AB=6,BC=8,将直角边AB折叠,使它落在斜边AC上,折痕为AD,则BD的长为多少?(2001年荆门市中考题)解:在Rt△ABC中,
∵∠B=90°,AB=6,BC=8.
∴由勾股定理可得AC=10.
∵对折后重合的两个三角形全等,即
△ABD≌△AB′D
∴B′D=BD,AB′=AB
设BD=x,则在Rt△BDC中,
B′D=x,B′C=10-6=4 ,DC=8-x
∵
∴
解得x=3即BD=3
利用勾股定理构造方程求解。 在解一般三角形、梯形等一些图形的问题时,可以适当地添加辅助线构造直角三角形,然后利用解直角三角形,使问题得以解决. [小结]课 后练习1. 在△ABC中∠C=90° ∠B=2∠A 则cosA=______3. 已A是锐角且tanA=3 则40°
tanA = cot(90o-A) cotA = tan(90o-A) 三角函数应用三角函数是两边的比值,可以利用三角函数求边求角列关系式(列方程)已知直角三角形的两条直角边分别为6和8,
求斜边上的中线______,斜边上的高_______
在Rt△ABC中,∠C=90,直角边AC是直角边BC的2倍,求∠B的四个三角函数锐角三角函数(复习)☆ 应用练习1.已知角,求值2.已知值,求角∠A=60°∠A=30°练习:在Rt△ABC中,∠C=90°:⑴已知∠A、 c, 则
a=____________;b=___________。⑶已知∠A、 a,
则b=____________; c=_________。7、解直角三角形中,经常接触的名称:铅
垂
线视线视线仰角俯角))h8、解直角三角形中,经常接触的名称:)方向角 如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)解直角三角形中,经常接触的名称: 星期天,小华去图书超市购书,他乘电梯上楼,已知电梯AB段的长度8 m,倾斜角为300,则二楼的高度BC段是________mABC30048问题一D问题三:双直角三角形 在山脚A处测得山顶B的仰角为45°. 沿着水平地面向前300m到达D点,在D点测得山顶B的仰角为60 0,求山高BC.如图,在地面A点测得山顶上铁塔BD的塔顶和塔底的仰角分别是α= 600, β= 450,已知塔高BD=100m,求山高CD.ABCDαβ变式1 如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为100米,求河的宽度.问题四:变式2变式3 已知铁塔塔基距楼房基水平距离BD为50米,由楼顶A望塔顶的仰角为45 o,由楼顶望塔底的俯角为30o,塔高DC为 ( )米D问题1楼房AB的高度是多少?问题2楼房CD的高度是多少?变式4 已知堤坝的横断面是梯形ABCD,上底CD 的宽为4,,坝高为4,坡角∠A=60°,坡角∠B=45°,求下底AB 的宽.变式5FE如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=8m,BC=5m,请你帮助计算一下这块花圃的面积?D30085变式611、如图,已知在Rt△ABC中,∠ACB=90度, CD是中线,P是CD上一点(P与C,D可以重合),BC=5,AC=12.
(1)若设CP=x,S△ACP=y,写出y与x 之间的函数关系式,并指出x的取值范围。
(2)求当y=10时,cot∠PAC的值。ACBDP练4.求tan15 °, tan22.5 °, tan75 ° 思 考在Rt△ABC中,∠C=90°斜边AB=2,直角边AC=1,∠ABC=30°,延长CB到D,连接AD使∠D=15°求tan15°的值。DACB北AC52° 22°B东东68°解:依题意得 ∠CBD=22°∠ABD=52°-22°=30°
∠BCA=22°+68°=90°
∵BC=2×30=60(海里)
∴AC=BC·sin30°=60×1/2=30(海里)
答:A、C的距离是30海里。
D练1.一船在海上B处以每小时30海里的速度,沿南偏东220方向航行,同时在B 处测得灯塔A 在南偏东520的方向上,航行2小时后到达C处,又测得灯塔A在北偏东680方向上,求A、C的距离。练2.(2000年广东中考题)在Rt△ABC中,E是斜边AB上的一点,把Rt△ABC沿CE折叠,点A与点B恰好重合,如果AC=4cm,求AB的长。解:由题意知:AC=BC
又:AC⊥BC
∴
∴
∴
即AB长为练3.如图,有一块直角三角形的纸片,两直角边AB=6,BC=8,将直角边AB折叠,使它落在斜边AC上,折痕为AD,则BD的长为多少?(2001年荆门市中考题)解:在Rt△ABC中,
∵∠B=90°,AB=6,BC=8.
∴由勾股定理可得AC=10.
∵对折后重合的两个三角形全等,即
△ABD≌△AB′D
∴B′D=BD,AB′=AB
设BD=x,则在Rt△BDC中,
B′D=x,B′C=10-6=4 ,DC=8-x
∵
∴
解得x=3即BD=3
利用勾股定理构造方程求解。 在解一般三角形、梯形等一些图形的问题时,可以适当地添加辅助线构造直角三角形,然后利用解直角三角形,使问题得以解决. [小结]课 后练习1. 在△ABC中∠C=90° ∠B=2∠A 则cosA=______3. 已A是锐角且tanA=3 则40°
