2023-2024学年沪科版八年级数学上册期末复习综合检测试题(无答案)
文档属性
| 名称 | 2023-2024学年沪科版八年级数学上册期末复习综合检测试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 383.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 10:19:00 | ||
图片预览

文档简介
期末复习综合检测试题
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1下列微信表情图标属于轴对称图形的是( )
A. B. C. D.
2.下列命题是真命题的是
A.如果,那么
B.如果,那么,
C.如果,那么
D.如果直线,,那么直线
3.以下列数字为长度的各组线段中,能构成三角形的有( )
A. 1 ,2 ,4 B. 4 ,3 ,1 C. 3 ,4 ,5 D. 2 ,4 ,2
4.下列所给条件中,能画出唯一的的是( )
A. B.
C. D.
5. 下列图形中,与关于直线成轴对称的是( )
A. B. C. D.
6 象棋在中国有着三千多年的历史,属于二人对抗性游戏的一种由于用具简单,趣味性强,成为流行极为广泛的棋艺活动如图是一方的棋盘如果“帅”坐标是,“卒”坐标是,那么“马”坐标是( )
A. B. C. D.
7. 有以下四个命题:其中正确的个数为( )。
(1)两条对角线互相平分的四边形是平行四边形;
(2)两条对角线相等的四边形是矩形;
(3)两条对角线互相垂直的平行四边形是菱形;
(4)有一组邻边相等且有一个角是直角的四边形是正方形;
A. 1 B. 2 C. 3 D. 4
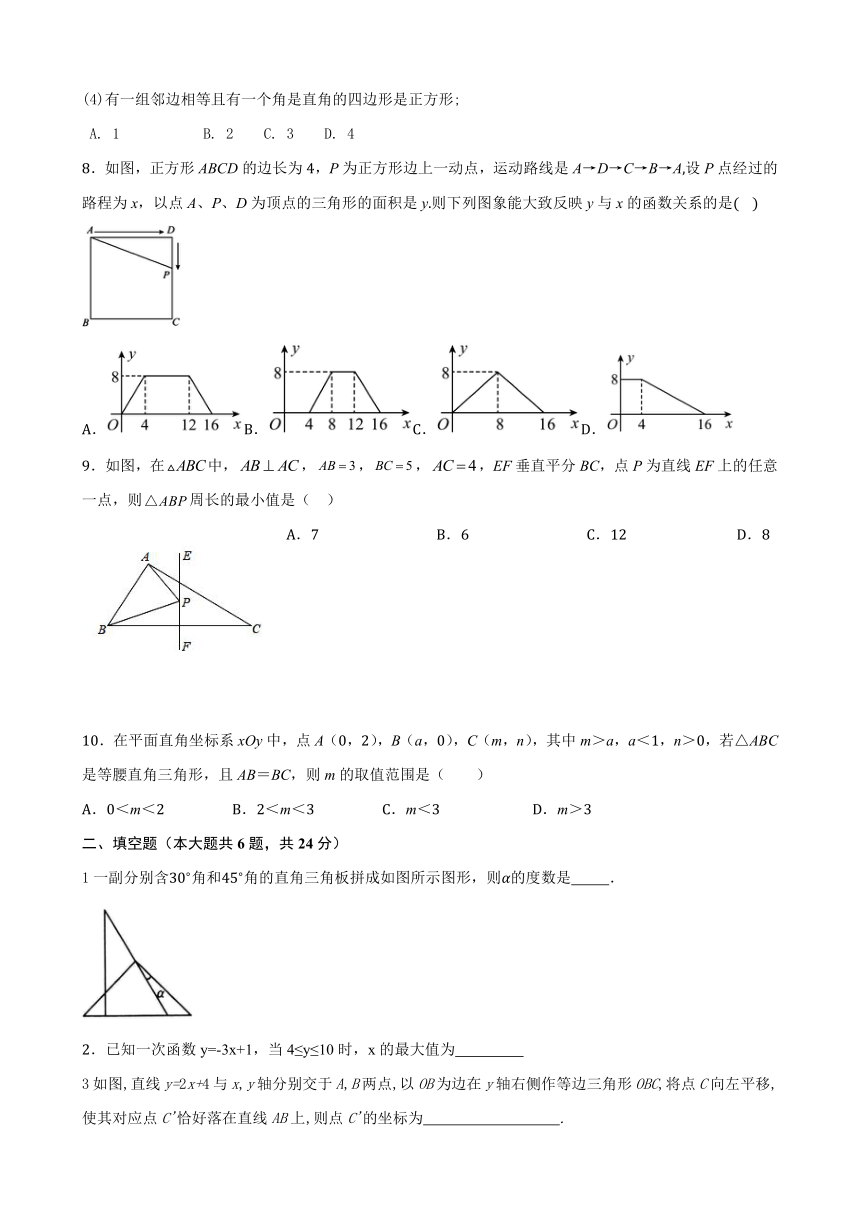
8.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是( )
A.B.C.D.
9.如图,在中,,,,,EF垂直平分BC,点P为直线EF上的任意一点,则周长的最小值是( )
A.7 B.6 C.12 D.8
10.在平面直角坐标系xOy中,点A(0,2),B(a,0),C(m,n),其中m>a,a<1,n>0,若△ABC是等腰直角三角形,且AB=BC,则m的取值范围是( )
A.0<m<2 B.2<m<3 C.m<3 D.m>3
二、填空题(本大题共6题,共24分)
1一副分别含角和角的直角三角板拼成如图所示图形,则的度数是 .
2.已知一次函数y=-3x+1,当4≤y≤10时,x的最大值为
3如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C'恰好落在直线AB上,则点C'的坐标为 .
4.已知三边的长分别为3,5,7,三边的长分别为3,7,,若这两个三角形全等,则 ______.
5.如图,在长方形中,点E在边上,连接,将沿折痕翻折,使点D落在边上的处,如果,那么___________度
6.已知三点,,在同一条直线上,则a的值为____________
三、解答题(共66分。解答应写出文字说明,证明过程或演算步骤)
1平面直角坐标系中,的三个顶点坐标分别为,,
试在平面直角坐标系中,画出;
求的面积;
若与关于x轴对称,请画出,并写出,,的坐标.
2在实数范围内因式分解
(1) (2)
3已知数a、b在数轴上的位置如图所示,化简:.
4如图,四边形中,,E为的中点,连结并延长交的延长线于点F.
(1)求证:;
(2)连结,当时,求的长.
5.是的外角,BE平分,CE平分,且BE、CE交于点
若,求:的度数.
猜想与的关系,并说明理由.
6直线:与x轴交于点D,直线:与x轴交于点A,且经过,两直线相交于点
求点C的坐标和直线的解析式;
求当x取何值,;
求的面积.
7某剧院举行新年专场音乐会,成人票每张40元,学生票每张10元,剧院制定了两种优惠方案,且每个团体购票时只能选择其中一种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的付款.某校有4名老师与名学生去观赏这次音乐会,设用方案1和方案2付款的总金额分别为元和元
分别求出、与x之间的函数关系式;
当学生人数为20名时,请通过计算说明哪种方案更优惠;
请通过计算说明:当学生人数为多少时,选择两种方案一样优惠?
8在和中,AC交DE于点O,,,,连接BE,
如图求证:;
如图2,延长DE交BC于点F,若,求的度数;
如图3,在的条件下,当时,过点C作交DF于点P,若,求的面积.
一、选择题(本大题共10小题,共30分。在每小题列出的选项中,选出符合题目的一项)
1下列微信表情图标属于轴对称图形的是( )
A. B. C. D.
2.下列命题是真命题的是
A.如果,那么
B.如果,那么,
C.如果,那么
D.如果直线,,那么直线
3.以下列数字为长度的各组线段中,能构成三角形的有( )
A. 1 ,2 ,4 B. 4 ,3 ,1 C. 3 ,4 ,5 D. 2 ,4 ,2
4.下列所给条件中,能画出唯一的的是( )
A. B.
C. D.
5. 下列图形中,与关于直线成轴对称的是( )
A. B. C. D.
6 象棋在中国有着三千多年的历史,属于二人对抗性游戏的一种由于用具简单,趣味性强,成为流行极为广泛的棋艺活动如图是一方的棋盘如果“帅”坐标是,“卒”坐标是,那么“马”坐标是( )
A. B. C. D.
7. 有以下四个命题:其中正确的个数为( )。
(1)两条对角线互相平分的四边形是平行四边形;
(2)两条对角线相等的四边形是矩形;
(3)两条对角线互相垂直的平行四边形是菱形;
(4)有一组邻边相等且有一个角是直角的四边形是正方形;
A. 1 B. 2 C. 3 D. 4
8.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是( )
A.B.C.D.
9.如图,在中,,,,,EF垂直平分BC,点P为直线EF上的任意一点,则周长的最小值是( )
A.7 B.6 C.12 D.8
10.在平面直角坐标系xOy中,点A(0,2),B(a,0),C(m,n),其中m>a,a<1,n>0,若△ABC是等腰直角三角形,且AB=BC,则m的取值范围是( )
A.0<m<2 B.2<m<3 C.m<3 D.m>3
二、填空题(本大题共6题,共24分)
1一副分别含角和角的直角三角板拼成如图所示图形,则的度数是 .
2.已知一次函数y=-3x+1,当4≤y≤10时,x的最大值为
3如图,直线y=2x+4与x,y轴分别交于A,B两点,以OB为边在y轴右侧作等边三角形OBC,将点C向左平移,使其对应点C'恰好落在直线AB上,则点C'的坐标为 .
4.已知三边的长分别为3,5,7,三边的长分别为3,7,,若这两个三角形全等,则 ______.
5.如图,在长方形中,点E在边上,连接,将沿折痕翻折,使点D落在边上的处,如果,那么___________度
6.已知三点,,在同一条直线上,则a的值为____________
三、解答题(共66分。解答应写出文字说明,证明过程或演算步骤)
1平面直角坐标系中,的三个顶点坐标分别为,,
试在平面直角坐标系中,画出;
求的面积;
若与关于x轴对称,请画出,并写出,,的坐标.
2在实数范围内因式分解
(1) (2)
3已知数a、b在数轴上的位置如图所示,化简:.
4如图,四边形中,,E为的中点,连结并延长交的延长线于点F.
(1)求证:;
(2)连结,当时,求的长.
5.是的外角,BE平分,CE平分,且BE、CE交于点
若,求:的度数.
猜想与的关系,并说明理由.
6直线:与x轴交于点D,直线:与x轴交于点A,且经过,两直线相交于点
求点C的坐标和直线的解析式;
求当x取何值,;
求的面积.
7某剧院举行新年专场音乐会,成人票每张40元,学生票每张10元,剧院制定了两种优惠方案,且每个团体购票时只能选择其中一种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的付款.某校有4名老师与名学生去观赏这次音乐会,设用方案1和方案2付款的总金额分别为元和元
分别求出、与x之间的函数关系式;
当学生人数为20名时,请通过计算说明哪种方案更优惠;
请通过计算说明:当学生人数为多少时,选择两种方案一样优惠?
8在和中,AC交DE于点O,,,,连接BE,
如图求证:;
如图2,延长DE交BC于点F,若,求的度数;
如图3,在的条件下,当时,过点C作交DF于点P,若,求的面积.
同课章节目录
