第4章 几何图形初步 期末综合复习训练题 2023-2024学年人教版七年级数学上册(含答案解析)
文档属性
| 名称 | 第4章 几何图形初步 期末综合复习训练题 2023-2024学年人教版七年级数学上册(含答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 550.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 00:00:00 | ||
图片预览



文档简介
2023-2024学年人教版七年级数学上册《第4章几何图形初步》
期末综合复习训练题(附答案)
一、单选题
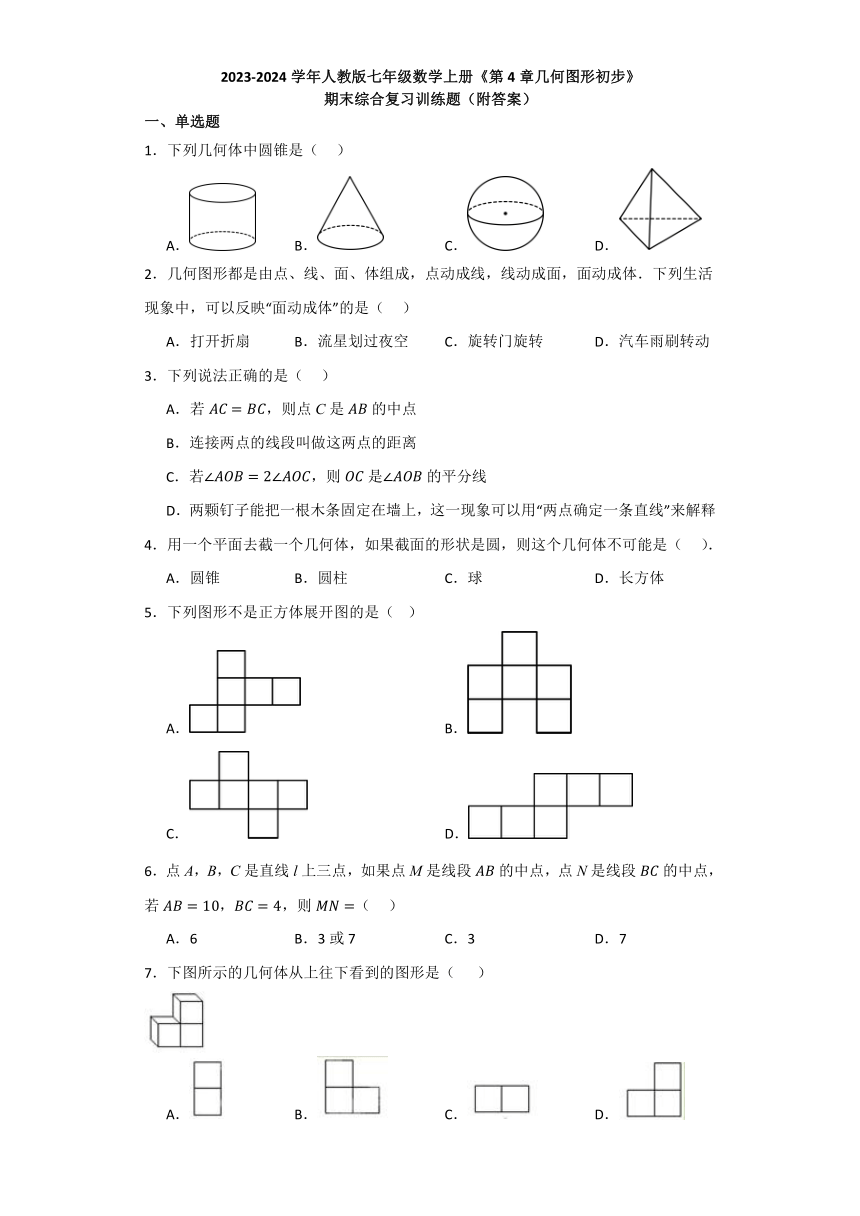
1.下列几何体中圆锥是( )
A. B. C. D.
2.几何图形都是由点、线、面、体组成,点动成线,线动成面,面动成体.下列生活现象中,可以反映“面动成体”的是( )
A.打开折扇 B.流星划过夜空 C.旋转门旋转 D.汽车雨刷转动
3.下列说法正确的是( )
A.若,则点C是的中点
B.连接两点的线段叫做这两点的距离
C.若,则是的平分线
D.两颗钉子能把一根木条固定在墙上,这一现象可以用“两点确定一条直线”来解释
4.用一个平面去截一个几何体,如果截面的形状是圆,则这个几何体不可能是( ).
A.圆锥 B.圆柱 C.球 D.长方体
5.下列图形不是正方体展开图的是( )
A. B.
C. D.
6.点A,B,C是直线l上三点,如果点M是线段的中点,点N是线段的中点,若,则( )
A.6 B.3或7 C.3 D.7
7.下图所示的几何体从上往下看到的图形是( )
A. B. C. D.
8.如图,已知直线和相交于点,是直角,平分,,则的大小为( )
A. B. C. D.
二、填空题
9.如图A、B、C、D四个图形,它们能折叠成的立体图形依次是 .
A.B.C.D.
10.如图:“小草青青,足下留情”,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一不文明现象的原因是: ,
11.(1)计算: .
(2)钟表上的时间是3时30分,此时时针与分针所成的夹角是 度.
12.如图,已知B,M,C依次为线段上的三点,M为的中点,且,.若,则线段的长为 .
13.将一个长6cm,宽3cm的长方形绕它的长边所在的直线旋转一周,所得几何体的体积为 cm3(结果保留π).
14.任意一个锐角的补角与这个锐角的余角的差等于 .
15.如图是由一些完全相同的小立方块所搭成的几何体分别从正面、左面、上面看所得到的图形,则这些小立方块一共有 个.
16.如图,,下列结论:①;②;③;④若平分,则平分.其中正确的有 .(填序号)
三、解答题
17.如图,在平面内有A、B、C三点.
(1)画直线,线段,射线
(2)在线段上任取一点D(不同于B、C),连接;
(3)数数看,此时图中线段共有 条.
18.如图,是由棱长均为的个大小相同的小立方块组成的简单几何体.
(1)请分别画出从正面、上面、左面三个方向看到的图形;
(2)该几何体的表面积为______.(包括底部)
19.如图是一个长方体纸盒的平面展开图,每个面都标有字母(字母在长方体的外表面),请根据下面的要求回答问题:
(1)如果面在长方体的底面,那么哪个面在上面?
(2)如果面在长方体前面,那么哪个面在后面?
(3)如果从前面能看到面,从上面能看到面,那么从左面能看到是哪个面?
20.如图,射线的方向是北偏东,射线的方向是北偏西,若,则射线的方向是北偏东多少度?
21.如图,延长至,使为的中点,点在上,.
(1) , ;
(2)若,求的长.
22.直线、相交于点O,平分.
(1)若,,求的度数;
(2)若平分,,求的度数.
23.如图,已知点、在线段上.
(1)图中共有________条线段;
(2)若比较线段的大小:________(填:“>”,“=”,或“<”);
(3)若,,是的中点,是的中点(如下图).
①求的长度;
②嘉嘉同学分析探究后说,当线段在射线上运动时,线段的长度不变.你同意他的说法吗?并说明理由.
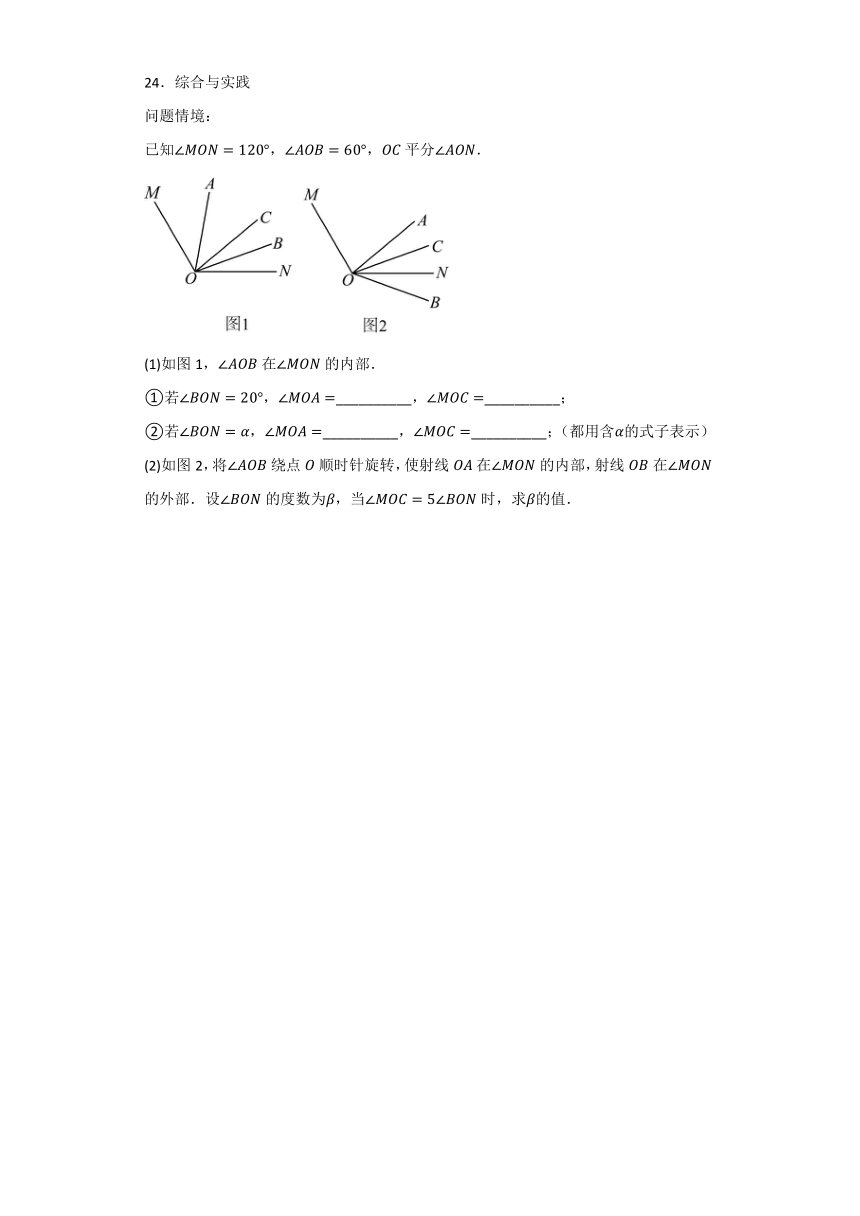
24.综合与实践
问题情境:
已知,,平分.
(1)如图1,在的内部.
①若,__________,__________;
②若,__________,__________;(都用含的式子表示)
(2)如图2,将绕点顺时针旋转,使射线在的内部,射线在的外部.设的度数为,当时,求的值.
参考答案
1.解:由图可知,A选项为圆柱,B选项为圆锥,C选项为球,D选项为三棱锥;
故选:B.
2.解:A、打开折扇是“线动成面”,故本选项不合题意;
B、流星划过夜空是“点动成线”,故本选项符合题意;
C、旋转门的旋转是“面动成体”,故本选项符合题意;
D、汽车雨刷的转动是“线动成面”,故本选项不合题意;
故选:C.
3.解:A、若,则当点C在线段上时,点C是的中点,点C不在线段上时,点C不是的中点,原说法错误,不符合题意;
B、连接两点的线段的长度叫做这两点的距离,原说法错误,不符合题意;
C、若,则当在的内部时,是的平分线,当在的外部时,不是的平分线,原说法错误,不符合题意;
D、两颗钉子能把一根木条固定在墙上,这一现象可以用“两点确定一条直线”来解释,原说法正确,符合题意;
故选:D.
4.解:长方体有六个面,用平面去截长方体时最多与六个面相交得六边形,最少与三个面相交得三角形,因为截面与长方体各面的交线为直线,
故此截面的形状不可能是圆.
故选:D.
5.解:、是正方体展开图,不合题意;
、折叠后有两个正方形重合,不是正方体展开图,符合题意;
、符合正方体展开图,不合题意;
、符合正方体展开图,不合题意;
故选:.
6.解:如图,点为线段的中点,点为线段的中点.,
,,
;
如图,点为线段的中点,点为线段的中点.,
,,
.
的长为或.
故选:B.
7.解:从上往下看所得到的图形是两个横着的正方形,上面的棱是能够看见的,所以用实线.
故选:C
8.解:是直角,,
,
平分,
,
,
.
故选:A.
9.解:A.侧面是长方形,两个底面是圆,所以叠成的立体图形是圆柱;
B. 侧面是长方形,两个底面是五边形,所以叠成的立体图形是五棱柱;
C. 侧面是扇形,底面是圆,所以叠成的立体图形是圆锥;
D. 侧面是3个长方形,两个底面是三角形,所以叠成的立体图形是三棱柱;
故答案为:圆柱,五棱柱,圆锥、三棱柱.
10.解:依题意,为抄近路践踏草坪是因为两点之间线段最短,
故答案为:两点之间线段最短.
11. (1)解:∵,
∴,
∴,
故答案为:;
(2)解:∵一个圆为,有12个大格,
∴一个大格为,
一个圆有60个小格,
∴一个小格为:,
∴3时30分夹角为:;
故答案为:75.
12.解:设,,
∵M为的中点,
∴,
,
又∵,
∴,
∴,
∴,
故答案为:18.
13.解:由题意得得:旋转得到的是圆柱.
∴体积为:
故答案为:
14.解:设这个锐角为x,依题意得:
.
故答案为:90.
15.解:综合从正面、左面、上面看所得到的图形,可得:底层有7个小正方体,第二层有2个小正方体,第三层有1个小正方体,
这些小立方块一共有:个,
故答案为:10.
16.解:∵,
∴,即,故①正确;
∵,
∴,而得不到,故②错误;
∴,
∴,故③正确;
∵平分,
∴,
∵,
∴,
∴平分,故④正确,
故答案为:①③④.
17.(1)解:如图所示:
(2)解:如图所示:
(3)解:图中有线段6条,即线段,,,,,,
故答案为:6.
18.(1)解:如图所示.
(2)该几何体的表面积为:.
故答案为:.
19.(1)解:面与面是对面,面在长方体的底面,面在上面;
(2)解:面与面是对面,面在长方体前面,面在后面;
(3)解:、、面是邻面,从前面能看到面,从上面能看到面,面在左面.
20.解:如图,由题意知,,
∴,
∴,
故射线的方向是北偏东.
21.(1)解:∵B是的中点,
∴.
∵,
∴.
∴.
故答案为:;
(2)∵,
∴.
∴.
∵,
∴.
22.解:(1)平分,
,
;
(2)设,
平分,
,
平分,
,
由题意得,,
解得,,
.
23.(1)解:∵、在线段上,
∴图中共有线段共6条.
故答案为:6;
(2)若,则,即.
故答案为:;
(3)①∵,
∴,
∵是的中点,是的中点,
∴,
∴,
∴.
②当线段在射线上运动时,
当点在线段上,点在射线上运动时:
∵,
∴,
∵是的中点,是的中点,
∴,
∴,
∴.
当点在射线上,点在射线上运动时:
∵,
∴,
∵是的中点,是的中点,
∴,
∴,
∴.
∴线段的长度不变.
24.(1)解:①∵,,,
∴,,
∵平分,
∴,
∴,
故答案为:;;
②∵,,,
∴,,
∵平分,
∴,
∴,
故答案为:;;
(2)解:∵,,,
∴.
∵平分,
∴.
∵,
∴.
∵,
∴,
∴,
∴。
期末综合复习训练题(附答案)
一、单选题
1.下列几何体中圆锥是( )
A. B. C. D.
2.几何图形都是由点、线、面、体组成,点动成线,线动成面,面动成体.下列生活现象中,可以反映“面动成体”的是( )
A.打开折扇 B.流星划过夜空 C.旋转门旋转 D.汽车雨刷转动
3.下列说法正确的是( )
A.若,则点C是的中点
B.连接两点的线段叫做这两点的距离
C.若,则是的平分线
D.两颗钉子能把一根木条固定在墙上,这一现象可以用“两点确定一条直线”来解释
4.用一个平面去截一个几何体,如果截面的形状是圆,则这个几何体不可能是( ).
A.圆锥 B.圆柱 C.球 D.长方体
5.下列图形不是正方体展开图的是( )
A. B.
C. D.
6.点A,B,C是直线l上三点,如果点M是线段的中点,点N是线段的中点,若,则( )
A.6 B.3或7 C.3 D.7
7.下图所示的几何体从上往下看到的图形是( )
A. B. C. D.
8.如图,已知直线和相交于点,是直角,平分,,则的大小为( )
A. B. C. D.
二、填空题
9.如图A、B、C、D四个图形,它们能折叠成的立体图形依次是 .
A.B.C.D.
10.如图:“小草青青,足下留情”,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一不文明现象的原因是: ,
11.(1)计算: .
(2)钟表上的时间是3时30分,此时时针与分针所成的夹角是 度.
12.如图,已知B,M,C依次为线段上的三点,M为的中点,且,.若,则线段的长为 .
13.将一个长6cm,宽3cm的长方形绕它的长边所在的直线旋转一周,所得几何体的体积为 cm3(结果保留π).
14.任意一个锐角的补角与这个锐角的余角的差等于 .
15.如图是由一些完全相同的小立方块所搭成的几何体分别从正面、左面、上面看所得到的图形,则这些小立方块一共有 个.
16.如图,,下列结论:①;②;③;④若平分,则平分.其中正确的有 .(填序号)
三、解答题
17.如图,在平面内有A、B、C三点.
(1)画直线,线段,射线
(2)在线段上任取一点D(不同于B、C),连接;
(3)数数看,此时图中线段共有 条.
18.如图,是由棱长均为的个大小相同的小立方块组成的简单几何体.
(1)请分别画出从正面、上面、左面三个方向看到的图形;
(2)该几何体的表面积为______.(包括底部)
19.如图是一个长方体纸盒的平面展开图,每个面都标有字母(字母在长方体的外表面),请根据下面的要求回答问题:
(1)如果面在长方体的底面,那么哪个面在上面?
(2)如果面在长方体前面,那么哪个面在后面?
(3)如果从前面能看到面,从上面能看到面,那么从左面能看到是哪个面?
20.如图,射线的方向是北偏东,射线的方向是北偏西,若,则射线的方向是北偏东多少度?
21.如图,延长至,使为的中点,点在上,.
(1) , ;
(2)若,求的长.
22.直线、相交于点O,平分.
(1)若,,求的度数;
(2)若平分,,求的度数.
23.如图,已知点、在线段上.
(1)图中共有________条线段;
(2)若比较线段的大小:________(填:“>”,“=”,或“<”);
(3)若,,是的中点,是的中点(如下图).
①求的长度;
②嘉嘉同学分析探究后说,当线段在射线上运动时,线段的长度不变.你同意他的说法吗?并说明理由.
24.综合与实践
问题情境:
已知,,平分.
(1)如图1,在的内部.
①若,__________,__________;
②若,__________,__________;(都用含的式子表示)
(2)如图2,将绕点顺时针旋转,使射线在的内部,射线在的外部.设的度数为,当时,求的值.
参考答案
1.解:由图可知,A选项为圆柱,B选项为圆锥,C选项为球,D选项为三棱锥;
故选:B.
2.解:A、打开折扇是“线动成面”,故本选项不合题意;
B、流星划过夜空是“点动成线”,故本选项符合题意;
C、旋转门的旋转是“面动成体”,故本选项符合题意;
D、汽车雨刷的转动是“线动成面”,故本选项不合题意;
故选:C.
3.解:A、若,则当点C在线段上时,点C是的中点,点C不在线段上时,点C不是的中点,原说法错误,不符合题意;
B、连接两点的线段的长度叫做这两点的距离,原说法错误,不符合题意;
C、若,则当在的内部时,是的平分线,当在的外部时,不是的平分线,原说法错误,不符合题意;
D、两颗钉子能把一根木条固定在墙上,这一现象可以用“两点确定一条直线”来解释,原说法正确,符合题意;
故选:D.
4.解:长方体有六个面,用平面去截长方体时最多与六个面相交得六边形,最少与三个面相交得三角形,因为截面与长方体各面的交线为直线,
故此截面的形状不可能是圆.
故选:D.
5.解:、是正方体展开图,不合题意;
、折叠后有两个正方形重合,不是正方体展开图,符合题意;
、符合正方体展开图,不合题意;
、符合正方体展开图,不合题意;
故选:.
6.解:如图,点为线段的中点,点为线段的中点.,
,,
;
如图,点为线段的中点,点为线段的中点.,
,,
.
的长为或.
故选:B.
7.解:从上往下看所得到的图形是两个横着的正方形,上面的棱是能够看见的,所以用实线.
故选:C
8.解:是直角,,
,
平分,
,
,
.
故选:A.
9.解:A.侧面是长方形,两个底面是圆,所以叠成的立体图形是圆柱;
B. 侧面是长方形,两个底面是五边形,所以叠成的立体图形是五棱柱;
C. 侧面是扇形,底面是圆,所以叠成的立体图形是圆锥;
D. 侧面是3个长方形,两个底面是三角形,所以叠成的立体图形是三棱柱;
故答案为:圆柱,五棱柱,圆锥、三棱柱.
10.解:依题意,为抄近路践踏草坪是因为两点之间线段最短,
故答案为:两点之间线段最短.
11. (1)解:∵,
∴,
∴,
故答案为:;
(2)解:∵一个圆为,有12个大格,
∴一个大格为,
一个圆有60个小格,
∴一个小格为:,
∴3时30分夹角为:;
故答案为:75.
12.解:设,,
∵M为的中点,
∴,
,
又∵,
∴,
∴,
∴,
故答案为:18.
13.解:由题意得得:旋转得到的是圆柱.
∴体积为:
故答案为:
14.解:设这个锐角为x,依题意得:
.
故答案为:90.
15.解:综合从正面、左面、上面看所得到的图形,可得:底层有7个小正方体,第二层有2个小正方体,第三层有1个小正方体,
这些小立方块一共有:个,
故答案为:10.
16.解:∵,
∴,即,故①正确;
∵,
∴,而得不到,故②错误;
∴,
∴,故③正确;
∵平分,
∴,
∵,
∴,
∴平分,故④正确,
故答案为:①③④.
17.(1)解:如图所示:
(2)解:如图所示:
(3)解:图中有线段6条,即线段,,,,,,
故答案为:6.
18.(1)解:如图所示.
(2)该几何体的表面积为:.
故答案为:.
19.(1)解:面与面是对面,面在长方体的底面,面在上面;
(2)解:面与面是对面,面在长方体前面,面在后面;
(3)解:、、面是邻面,从前面能看到面,从上面能看到面,面在左面.
20.解:如图,由题意知,,
∴,
∴,
故射线的方向是北偏东.
21.(1)解:∵B是的中点,
∴.
∵,
∴.
∴.
故答案为:;
(2)∵,
∴.
∴.
∵,
∴.
22.解:(1)平分,
,
;
(2)设,
平分,
,
平分,
,
由题意得,,
解得,,
.
23.(1)解:∵、在线段上,
∴图中共有线段共6条.
故答案为:6;
(2)若,则,即.
故答案为:;
(3)①∵,
∴,
∵是的中点,是的中点,
∴,
∴,
∴.
②当线段在射线上运动时,
当点在线段上,点在射线上运动时:
∵,
∴,
∵是的中点,是的中点,
∴,
∴,
∴.
当点在射线上,点在射线上运动时:
∵,
∴,
∵是的中点,是的中点,
∴,
∴,
∴.
∴线段的长度不变.
24.(1)解:①∵,,,
∴,,
∵平分,
∴,
∴,
故答案为:;;
②∵,,,
∴,,
∵平分,
∴,
∴,
故答案为:;;
(2)解:∵,,,
∴.
∵平分,
∴.
∵,
∴.
∵,
∴,
∴,
∴。
