第二章 整式的加减 期末练习(含答案)2023--2024学年人教版七年级数学上册
文档属性
| 名称 | 第二章 整式的加减 期末练习(含答案)2023--2024学年人教版七年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 360.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 10:32:49 | ||
图片预览



文档简介
人教版(2012)数学七年级上册第二章整式的加减期末章节拔高练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若单项式与的和是单项式,则的值是( )
A. B.6 C. D.9
2.如图图案由“火柴棍”拼搭而成,第1个图案有4根火柴棍,第2个图案有7根火柴棍,第3个图案有10根火柴棍,,则第n个图案的“火柴棍”根数是
A. B. C. D.
3.如图为某三岔路口交通环岛的简化模型.在某高峰时段,单位时间进出路口A,B,C的机动车辆数如图所示.图中分别表示该时段单位时间通过路段的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则的大小关系(用“”“”或“”连接)是( )
A. B. C. D.
4.一个两位数,十位上的数字为a,个位上的数字比十位上的数字少2,则这个两位数为( )
A.11a-20 B.11a+20 C.11a-2 D.11a+2
5.下列说法正确的是( )
A.不是单项式 B.的系数是
C.的次数是 D.的次数是
6.若,则等于( )
A.0 B.1 C.2 D.3
7.下列运算正确的是( )
A. B. C. D.
8.把–3+(–2)–(+1)改为省略加号的和的形式是( )
A.–3+2+1 B.–3–2+1
C.–3–2–1 D.–3+2–1
9.若与是同类项,则的相反数是( )
A. B. C. D.
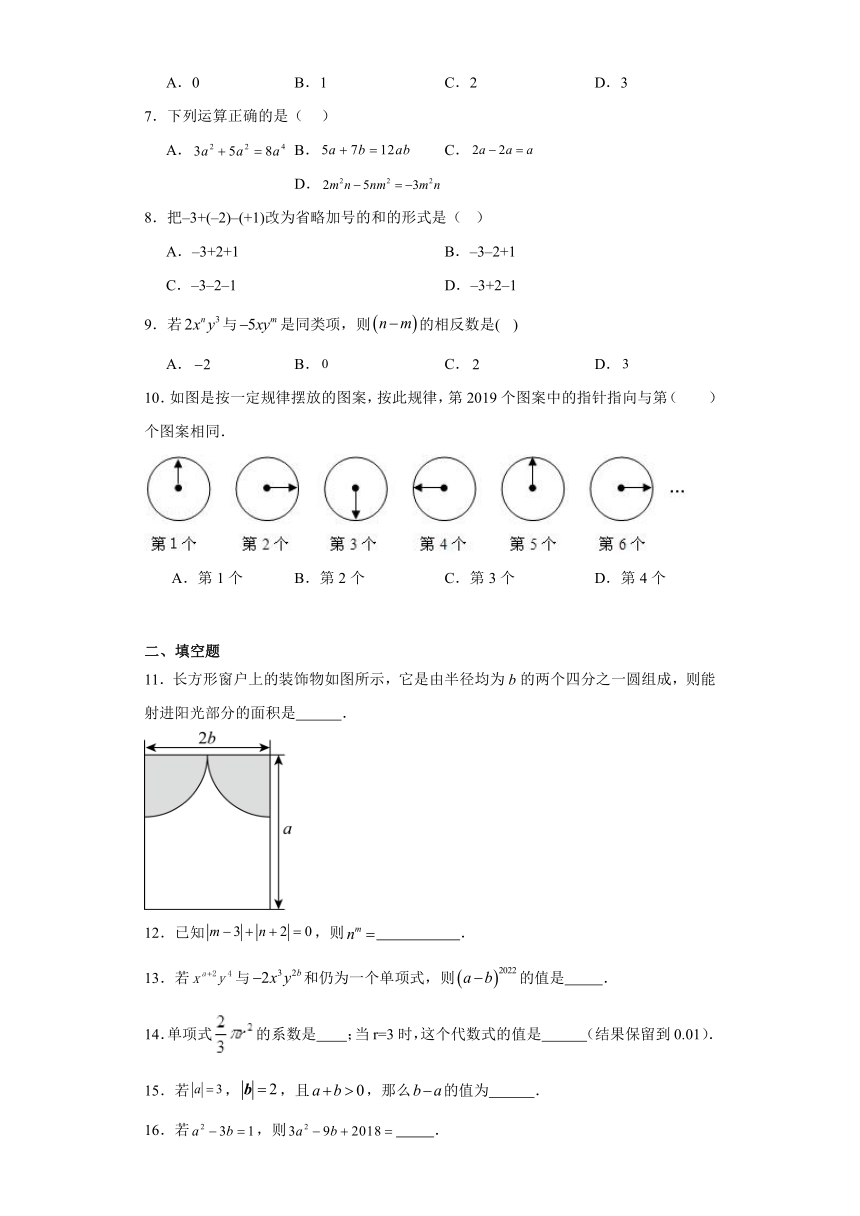
10.如图是按一定规律摆放的图案,按此规律,第2019个图案中的指针指向与第( )个图案相同.
A.第1个 B.第2个 C.第3个 D.第4个
二、填空题
11.长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是 .
12.已知,则 .
13.若与和仍为一个单项式,则的值是 .
14.单项式的系数是 ;当r=3时,这个代数式的值是 (结果保留到0.01).
15.若,,且,那么的值为 .
16.若,则 .
17. , .
18.等边在数轴上的位置如图所示,点对应的数分别为0和,若绕着顶点逆时针方向在数轴上连续翻转,翻转1次后,点所对应的数为;则翻转2023次后,点所对应的数是 .
19.若﹣xm﹣5y与2x3yn﹣2是同类项,则m+n= .
20.某粮食公司2019年生产大米的总量为a万吨,2020年比2019年生产大米的总量增加了20%,则2020年生产大米的总量为 万吨.
三、解答题
21.学校体育节要举办足球赛,若有5支球队进行单循环比赛(即全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场),则该校一共要安排多少场比赛?
构建模型:
生活中的许多实际问题,往往需要构建相应的数学模型,利用模型的思想来解决问题.
为解决上述问题,我们构建如下数学模型:
(1)如图①,我们可以在平面内画出5个点(任意3个点都不在同一条直线上),其中每个点各代表一支足球队,两支球队之间比赛一场就用一条线段把它们连接起来.由于每支球队都要与其他各队比赛一场,即每个点与另外4个点都可连成一条线段,这样一共连成条线段,而每两个点之间的线段都重复计算了一次,实际只有条线段,所以该校一共要安排10场比赛.
(2)若学校有6支足球队进行单循环比赛,借助图②,可知一共要安排______场比赛;
(3)根据以上规律,若学校有n支足球队进行单循环比赛,则一共要安排______场比赛.
实际应用:
(4)老师为了让数学兴趣班的同学互相认识,请班上35位同学每两个人都相互握一次手,全班同学总共握手_______次.
拓展提高:
(5)往返于深圳和潮汕的同一辆高速列车,中途经惠州、陆丰、普宁、潮阳4个车站(每种车票票面都印有上车站名称与下车站名称),那么在这段线路上往返行车,要准备多少种车票:请你求出来.
22.书是人类进步的阶梯!为爱护书一般都将书本用封皮包好,现有一本《数学杂谈》如图1,该书的长为21cm,宽为15cm,厚度为2cm,小华用一张长方形纸(如图2所示)包好了这本书.在图2的包书纸示意图中,虚线是折痕,阴影是裁掉的部分,四角均为大小相同的正方形,正方形的边长为折进去的宽度.设用该包书纸包这本书时折进去的宽度为acm.
(1)该包书纸的长为______cm,宽为______cm;(用含a的代数式表示)
(2)当时,求该包书纸的面积(含阴影部分).
23.已知A=-x-2y-1,B=x+y+1.
(1)求A+3B.
(2)当x+2y=6时,求A+3B的值.
24.定义:对于一个数x,我们把[x]称作x的相伴数;若x≥0,则[x]=x﹣1;若x<0,则[x]=x+1,例:[0.5]=﹣0.5
(1)求[]、[﹣1]的值;
(2)当a>0,b<0时,有[a]=[b]+1,试求代数式(b﹣a)3﹣3a+3b的值;
25.已知,.
(1)求的值;
(2)若,求的值.
26.若A=,B=,求2A-B的值.
27.某销售办公用品的商店推出两种优惠方案:
①购买1个书包,赠送1支水性笔.②书包和水性笔一律按九折优惠.
已知每个书包定价为20元,每支水性笔定价为5元.
(1)小丽和同学需买6个书包,支水性笔(不少于6支),请用含的代数式表示两种优惠方案,各需多少元.
(2)若两种方案只能选一种,当时,采用哪种方案更划算?
参考答案:
1.D
2.D
3.C
4.C
5.C
6.A
7.D
8.C
9.C
10.C
11.
12.
13.1
14. , 18.85.
15.或/或
16.2021
17.
18.
19.11
20.1.2a
21.(2)15;(3);(4)595;(5)要准备30种车票
22.(1);
(2)
23.(1)x+y+2;(2)5
24.(1);0(2)-36.
25.(1)
(2)
26.
27.(1)方案①需()元, 方案②需()元;(2)采用方案①更划算
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若单项式与的和是单项式,则的值是( )
A. B.6 C. D.9
2.如图图案由“火柴棍”拼搭而成,第1个图案有4根火柴棍,第2个图案有7根火柴棍,第3个图案有10根火柴棍,,则第n个图案的“火柴棍”根数是
A. B. C. D.
3.如图为某三岔路口交通环岛的简化模型.在某高峰时段,单位时间进出路口A,B,C的机动车辆数如图所示.图中分别表示该时段单位时间通过路段的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等),则的大小关系(用“”“”或“”连接)是( )
A. B. C. D.
4.一个两位数,十位上的数字为a,个位上的数字比十位上的数字少2,则这个两位数为( )
A.11a-20 B.11a+20 C.11a-2 D.11a+2
5.下列说法正确的是( )
A.不是单项式 B.的系数是
C.的次数是 D.的次数是
6.若,则等于( )
A.0 B.1 C.2 D.3
7.下列运算正确的是( )
A. B. C. D.
8.把–3+(–2)–(+1)改为省略加号的和的形式是( )
A.–3+2+1 B.–3–2+1
C.–3–2–1 D.–3+2–1
9.若与是同类项,则的相反数是( )
A. B. C. D.
10.如图是按一定规律摆放的图案,按此规律,第2019个图案中的指针指向与第( )个图案相同.
A.第1个 B.第2个 C.第3个 D.第4个
二、填空题
11.长方形窗户上的装饰物如图所示,它是由半径均为b的两个四分之一圆组成,则能射进阳光部分的面积是 .
12.已知,则 .
13.若与和仍为一个单项式,则的值是 .
14.单项式的系数是 ;当r=3时,这个代数式的值是 (结果保留到0.01).
15.若,,且,那么的值为 .
16.若,则 .
17. , .
18.等边在数轴上的位置如图所示,点对应的数分别为0和,若绕着顶点逆时针方向在数轴上连续翻转,翻转1次后,点所对应的数为;则翻转2023次后,点所对应的数是 .
19.若﹣xm﹣5y与2x3yn﹣2是同类项,则m+n= .
20.某粮食公司2019年生产大米的总量为a万吨,2020年比2019年生产大米的总量增加了20%,则2020年生产大米的总量为 万吨.
三、解答题
21.学校体育节要举办足球赛,若有5支球队进行单循环比赛(即全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场),则该校一共要安排多少场比赛?
构建模型:
生活中的许多实际问题,往往需要构建相应的数学模型,利用模型的思想来解决问题.
为解决上述问题,我们构建如下数学模型:
(1)如图①,我们可以在平面内画出5个点(任意3个点都不在同一条直线上),其中每个点各代表一支足球队,两支球队之间比赛一场就用一条线段把它们连接起来.由于每支球队都要与其他各队比赛一场,即每个点与另外4个点都可连成一条线段,这样一共连成条线段,而每两个点之间的线段都重复计算了一次,实际只有条线段,所以该校一共要安排10场比赛.
(2)若学校有6支足球队进行单循环比赛,借助图②,可知一共要安排______场比赛;
(3)根据以上规律,若学校有n支足球队进行单循环比赛,则一共要安排______场比赛.
实际应用:
(4)老师为了让数学兴趣班的同学互相认识,请班上35位同学每两个人都相互握一次手,全班同学总共握手_______次.
拓展提高:
(5)往返于深圳和潮汕的同一辆高速列车,中途经惠州、陆丰、普宁、潮阳4个车站(每种车票票面都印有上车站名称与下车站名称),那么在这段线路上往返行车,要准备多少种车票:请你求出来.
22.书是人类进步的阶梯!为爱护书一般都将书本用封皮包好,现有一本《数学杂谈》如图1,该书的长为21cm,宽为15cm,厚度为2cm,小华用一张长方形纸(如图2所示)包好了这本书.在图2的包书纸示意图中,虚线是折痕,阴影是裁掉的部分,四角均为大小相同的正方形,正方形的边长为折进去的宽度.设用该包书纸包这本书时折进去的宽度为acm.
(1)该包书纸的长为______cm,宽为______cm;(用含a的代数式表示)
(2)当时,求该包书纸的面积(含阴影部分).
23.已知A=-x-2y-1,B=x+y+1.
(1)求A+3B.
(2)当x+2y=6时,求A+3B的值.
24.定义:对于一个数x,我们把[x]称作x的相伴数;若x≥0,则[x]=x﹣1;若x<0,则[x]=x+1,例:[0.5]=﹣0.5
(1)求[]、[﹣1]的值;
(2)当a>0,b<0时,有[a]=[b]+1,试求代数式(b﹣a)3﹣3a+3b的值;
25.已知,.
(1)求的值;
(2)若,求的值.
26.若A=,B=,求2A-B的值.
27.某销售办公用品的商店推出两种优惠方案:
①购买1个书包,赠送1支水性笔.②书包和水性笔一律按九折优惠.
已知每个书包定价为20元,每支水性笔定价为5元.
(1)小丽和同学需买6个书包,支水性笔(不少于6支),请用含的代数式表示两种优惠方案,各需多少元.
(2)若两种方案只能选一种,当时,采用哪种方案更划算?
参考答案:
1.D
2.D
3.C
4.C
5.C
6.A
7.D
8.C
9.C
10.C
11.
12.
13.1
14. , 18.85.
15.或/或
16.2021
17.
18.
19.11
20.1.2a
21.(2)15;(3);(4)595;(5)要准备30种车票
22.(1);
(2)
23.(1)x+y+2;(2)5
24.(1);0(2)-36.
25.(1)
(2)
26.
27.(1)方案①需()元, 方案②需()元;(2)采用方案①更划算
