人教版八年级数学上册第十四章《整式的乘法与因式分解》同步练习题(含答案)
文档属性
| 名称 | 人教版八年级数学上册第十四章《整式的乘法与因式分解》同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 41.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 10:41:08 | ||
图片预览



文档简介
八年级数学上册第十四章《整式乘法与因式分解》同步练习题
学校:______姓名:______班级:______
一、单选题
1.若,则的关系是()
A. B. C. D.
2.若,,,则下列关系正确的是( )
A.>> B.>> C.>> D.>>
3.计算的结果是( )
A. B. C. D.
4.下面式子从左边到右边的变形是因式分解的是( )
A.() B.
C.()() D.()
5.某同学粗心大意,分解因式时,把等式■▲中的两个数字弄污了,则式子中的■,▲对应的一组数字可以
是( ).
A., B., C., D.,
6.如图,正方形中阴影部分的面积为( )
A. B. C. D.
二、填空题
7., .
8.若,则 .
9.若,则的值是 .
10.已知,,则()() .
11.已知则 .
12.在的运算结果中的系数是,那么的值是 .
三、解答题
13.计算:
(1)
(2).
14.将下列各式因式分解:
(1)
(2)
(3)
(4)()()
15.先化简,再求值:()()(),其中,.
16.已知为正整数,且,求的值.
17.若的展开式中项的系数为项的系数为求的值
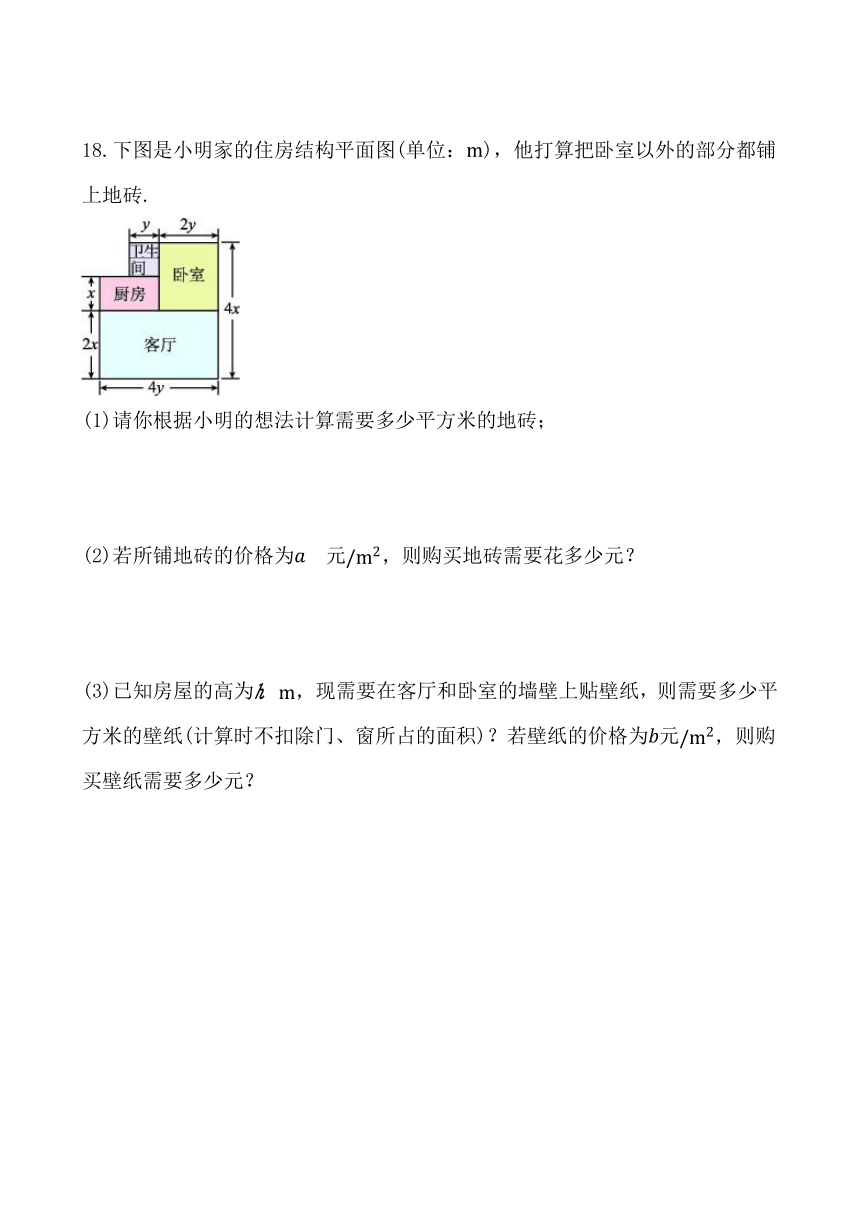
18.下图是小明家的住房结构平面图(单位:),他打算把卧室以外的部分都铺上地砖.
(1)请你根据小明的想法计算需要多少平方米的地砖;
(2)若所铺地砖的价格为 元则购买地砖需要花多少元?
(3)已知房屋的高为现需要在客厅和卧室的墙壁上贴壁纸,则需要多少平方米的壁纸(计算时不扣除门、窗所占的面积)?若壁纸的价格为元则购买壁纸需要多少元?
参考答案
1.【答案】C
2.【答案】B
【解析】∵,,,∴>>,
故选.
3.【答案】C
4.【答案】B
【解析】根据因式分解的意义求解即可.
本题考查了因式分解的意义,把多项式转化成几个整式积的形式.
解:、没把多项式转化成几个整式积的形式,故不符合题意;
、把多项式转化成几个整式积的形式,故符合题意;
、是整式的乘法,故不符合题意;
、没把多项式转化成几个整式积的形式,故不符合题意;
故选:.
5.【答案】A
【解析】【分析】
此题考查了学生用平方差公式分解因式的掌握情况,灵活性比较强平方差公式: 可以看出此题是用平方差公式分解因式,可以根据整式乘法与因式分解是互逆运算变形得出
【解答】
解:由▲得出▲,
则,则■.
故选.
6.【答案】D
【解析】.
7.【答案】
【解析】().据此可知答案为:.
8.【答案】
【解析】∵,,,
∴,
∴
9.【答案】
10.【答案】
【解析】当,时,
()()
()
,
据此可知答案为:.
本题主要考查了多项式乘多项式的相关知识点,需要掌握多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加才能正确解答此题.
11.【答案】
【解析】因为所以解得所以.
故答案为.
12.【答案】
【解析】
.
运算结果中的系数是
解得.
故答案为.
13.【答案】(1)解:原式
(2)原式
14.【答案】(1)解:原式();
(2)原式();
(3)原式()()();
(4)原式()()()()().
【解析】(1)根据提公因式法,可得答案;
(2)根据完全平方公式,可得答案;
(3)根据提公因式法,可得平方差公式,根据平方差公式,可得答案;
(4)根据提公因式法,可得平方差公式,根据平方差公式,可得答案.
本题考查了因式分解,一提,二套,三检查,分解要彻底.
15.【答案】解:()()(),
,
,
当,时,
原式();
【解析】先算乘法和除法,再合并同类项,最后代入求出即可.
16.【答案】∵,
∴
17.【答案】解:
.
因为展开式中项的系数为项的系数为
所以,
解得
所以.
18.【答案】(1)
(2) 元
(3);元.
学校:______姓名:______班级:______
一、单选题
1.若,则的关系是()
A. B. C. D.
2.若,,,则下列关系正确的是( )
A.>> B.>> C.>> D.>>
3.计算的结果是( )
A. B. C. D.
4.下面式子从左边到右边的变形是因式分解的是( )
A.() B.
C.()() D.()
5.某同学粗心大意,分解因式时,把等式■▲中的两个数字弄污了,则式子中的■,▲对应的一组数字可以
是( ).
A., B., C., D.,
6.如图,正方形中阴影部分的面积为( )
A. B. C. D.
二、填空题
7., .
8.若,则 .
9.若,则的值是 .
10.已知,,则()() .
11.已知则 .
12.在的运算结果中的系数是,那么的值是 .
三、解答题
13.计算:
(1)
(2).
14.将下列各式因式分解:
(1)
(2)
(3)
(4)()()
15.先化简,再求值:()()(),其中,.
16.已知为正整数,且,求的值.
17.若的展开式中项的系数为项的系数为求的值
18.下图是小明家的住房结构平面图(单位:),他打算把卧室以外的部分都铺上地砖.
(1)请你根据小明的想法计算需要多少平方米的地砖;
(2)若所铺地砖的价格为 元则购买地砖需要花多少元?
(3)已知房屋的高为现需要在客厅和卧室的墙壁上贴壁纸,则需要多少平方米的壁纸(计算时不扣除门、窗所占的面积)?若壁纸的价格为元则购买壁纸需要多少元?
参考答案
1.【答案】C
2.【答案】B
【解析】∵,,,∴>>,
故选.
3.【答案】C
4.【答案】B
【解析】根据因式分解的意义求解即可.
本题考查了因式分解的意义,把多项式转化成几个整式积的形式.
解:、没把多项式转化成几个整式积的形式,故不符合题意;
、把多项式转化成几个整式积的形式,故符合题意;
、是整式的乘法,故不符合题意;
、没把多项式转化成几个整式积的形式,故不符合题意;
故选:.
5.【答案】A
【解析】【分析】
此题考查了学生用平方差公式分解因式的掌握情况,灵活性比较强平方差公式: 可以看出此题是用平方差公式分解因式,可以根据整式乘法与因式分解是互逆运算变形得出
【解答】
解:由▲得出▲,
则,则■.
故选.
6.【答案】D
【解析】.
7.【答案】
【解析】().据此可知答案为:.
8.【答案】
【解析】∵,,,
∴,
∴
9.【答案】
10.【答案】
【解析】当,时,
()()
()
,
据此可知答案为:.
本题主要考查了多项式乘多项式的相关知识点,需要掌握多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加才能正确解答此题.
11.【答案】
【解析】因为所以解得所以.
故答案为.
12.【答案】
【解析】
.
运算结果中的系数是
解得.
故答案为.
13.【答案】(1)解:原式
(2)原式
14.【答案】(1)解:原式();
(2)原式();
(3)原式()()();
(4)原式()()()()().
【解析】(1)根据提公因式法,可得答案;
(2)根据完全平方公式,可得答案;
(3)根据提公因式法,可得平方差公式,根据平方差公式,可得答案;
(4)根据提公因式法,可得平方差公式,根据平方差公式,可得答案.
本题考查了因式分解,一提,二套,三检查,分解要彻底.
15.【答案】解:()()(),
,
,
当,时,
原式();
【解析】先算乘法和除法,再合并同类项,最后代入求出即可.
16.【答案】∵,
∴
17.【答案】解:
.
因为展开式中项的系数为项的系数为
所以,
解得
所以.
18.【答案】(1)
(2) 元
(3);元.
