9.1.2 不等式的性质 课件
文档属性
| 名称 | 9.1.2 不等式的性质 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-01 00:00:00 | ||
图片预览








文档简介
课件41张PPT。等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
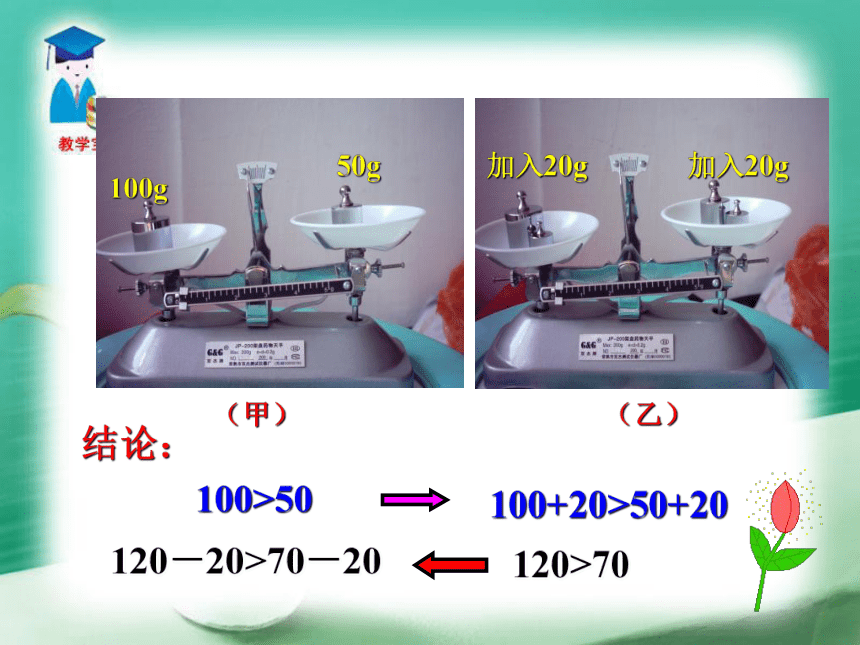
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.等式的这些性质适用于不等式吗?不等式有哪些性质呢?新课导入(甲)(乙)100g50g加入20g 加入20g结论:
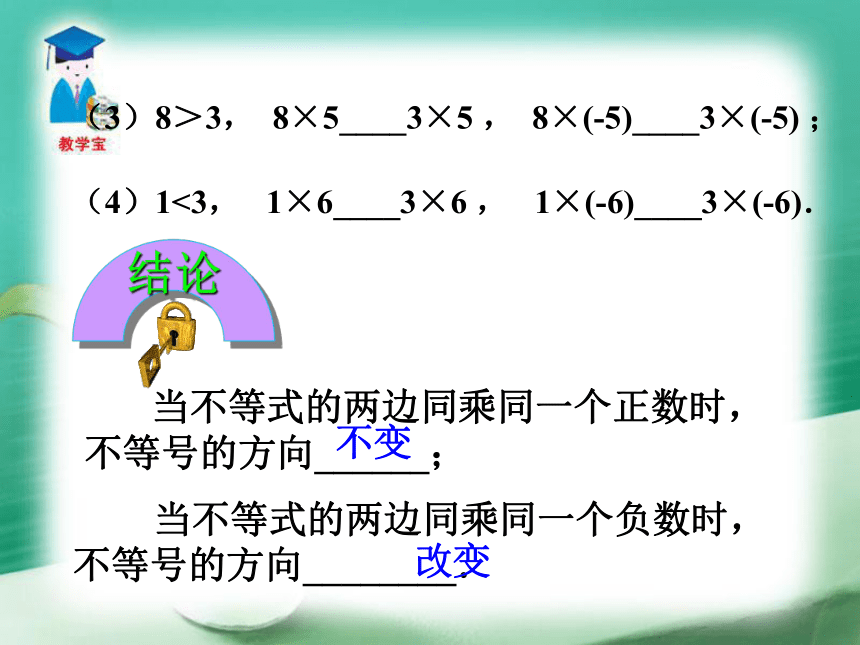
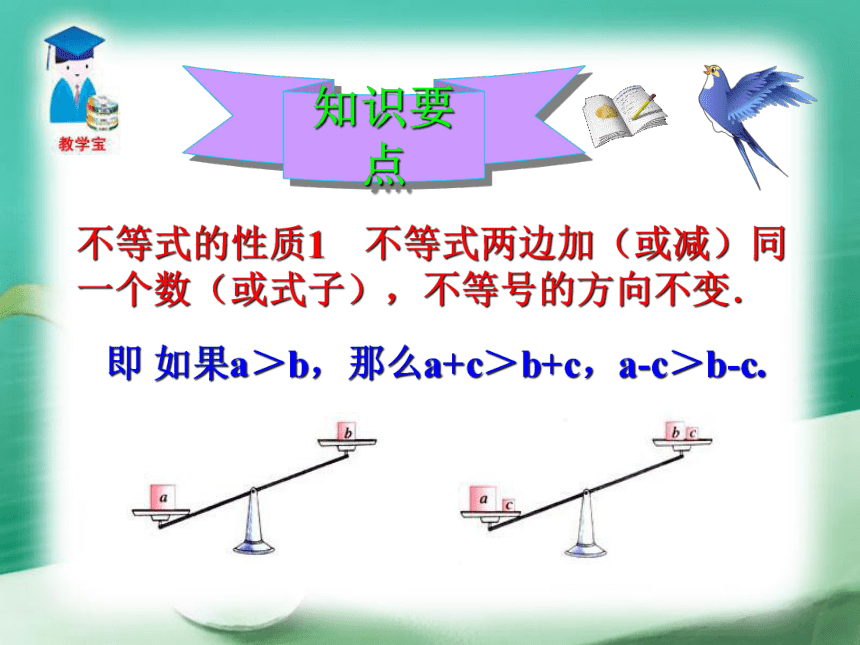
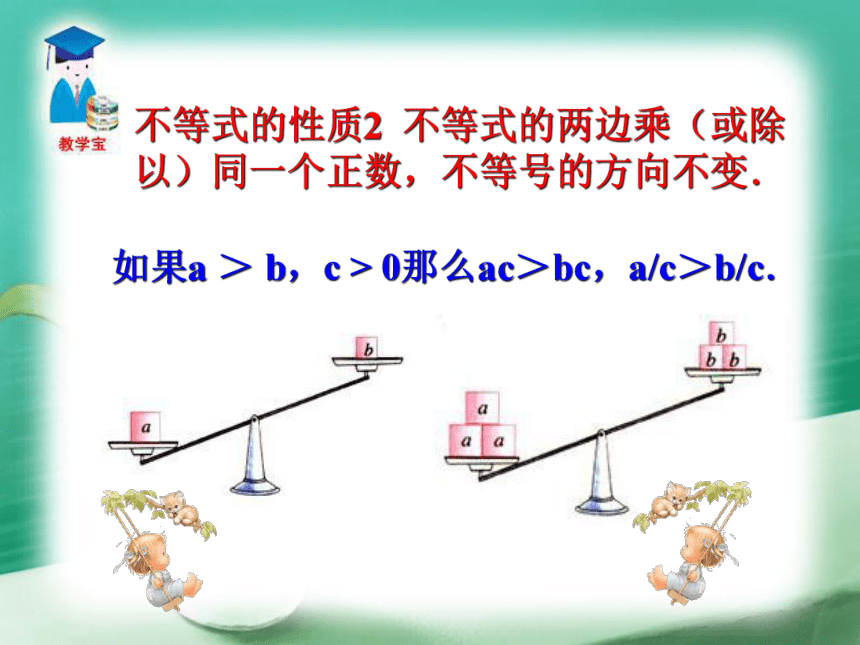
100>50100+20>50+20 120>70120-20>70-20用“<”或“>”填空,并找一找其中的规律.(2)2<5 , 2+3____5+3 , 2-3____5-3 ;(1)9>6, 9+3____6+3 , 9-3____9-3 ; 当不等式两边加或减去同一个数时,不等号的方向______.不变结论 当不等式的两边同乘同一个负数时,不等号的方向________. (3)8>3, 8×5____3×5 , 8×(-5)____3×(-5) ; (4)1<3, 1×6____3×6 , 1×(-6)____3×(-6). 当不等式的两边同乘同一个正数时,不等号的方向______;不变改变结论不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变. 即 如果a>b,那么a+c>b+c,a-c>b-c.知识要点不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.如果a > b,c > 0那么ac>bc,a/c>b/c.不等式的性质3 不等式两边乘(或除以)
同一个负数,不等号的方向改变.如果 a > b ,c < 0 那么 ac < bc,a/c < b/c.如果a>b,且c>d,那么a+c>b+d . 如果a>b,那么bb .如果a>b,且b>c,那么a>c.不等式的对称性:不等式的传递性:例1 用不等式的性质解下列不等式,并将解集在数轴上表示出来.
(1)x-6>15 (2)4x<3x-2
(3)-2x﹥50 (1)解:为了使不等式x-6>15中不等号的一边变为x,根据不等式的性质1,不等式两边都加6,不等号的方向不变,得
x-6+6﹥15+6,
x﹥21.这个不等式的解集在数轴上的表示如图,4x-3x﹤3x-2-3x
x﹤-2 (2)解 :为了使不等式3x<2x+1中不等号的一边变为x,根据不等式的性质1,不等式两边都减去3x,不等号的方向不变,得这个不等式的解在数轴上的表示如图, (3)解:为了使不等式-2x﹥50中的不等号的一边变为x,根据不等式的性质3,不等式两边都除以-2,不等号的方向改变,得x﹤-25这个不等式的解集在数轴上的表示如图.例2 已知a<0 ,试比较2a与a的大小.解法一:∵2>1,a<0,
∴2a<a(不等式的性质3) 解法二: 在数轴上分别表示2a和a的点(a<0),如图:2a位于a的左边,所以2a<a.解法三:∵ 2a-a=a, 又∵ a<0,
∴ 2a-a<0,
∴2a2b.加入后A,B两种产品的进口税分别为:(1-15%)a,(1-15%)b,∵ 1-15%>0∴(1-15%)a>2 (1-15%)b由不等式的基本性质3, 即表示产品A的进口税仍超过产品B的进口税的1倍以上.解:不等式x+3 <7的两边都减去3,得:
x+3 -3<7-3
∴x<4
而满足x<3的正整数有1,2,3,
所以不等式的正整数解为1,2,3.例6 求不等式x+3<7的正整数解.解一元一次不等式的一般步骤:(1)去分母:各项都乘以分母的最小公倍数;(2)去括号:注意符号问题;(3)移项:移项要变号;(4)合并同类项:系数相加,字母及字母的指
数不变; (5)系数化为1:不等式两边同除以未知数的系
数.(或同乘以未知数系数的倒数)解 :去分母,得
去括号,得
移项、得
合并同类项,得
两边都除以5,得 3(x-3) ≥2(8-x)
3x-9≥16-2x
3x+2x≥16+9
5x≥25
x≥5例7 利用不等式的性质解不等式.解:移项得:5x-4x>-4-10合并得x>-14例8 解不等式 5(x+2)>4x-4.去括号得:5x+10>4x-4解:移项得:2x-3x<-9-6合并得:-x<-15例9 解不等式 2(x+3)<3(x-3).去括号得:2x+6<3x-9x>15系数化为1得:例10 解不等式:解:去分母,得
3(2x+1) <2(13x-2) -4(6x+4)
去括号,得
6x+3<26x-4-24x-16
移项,得
6x-26x+24x<-4-16-3
合并,得
4x<-23 例11 当x取何正整数时,代数式 的值比 的值大1?解:根据题意,得 >1,
2(x+5)-3(3x-2)>6,
2x+10-9x+6>6,
-7x+16>6,
-7x>-10,
得 x<
所以,当x=1时,满足题意要求.一元一次不等式ax>b和ax(其中a、b都是已知数)的解集是 条件解集类型(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1在(1)与(5)这两步若乘以(或除以)负数,要把不等号方向改变两边同时除以未知数的系数一般只有一个解一般解集含有无数个解一元一次方程与一元一次不等式的解法步骤比较 不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变. 不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变. 不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.课堂小结解一元一次不等式的一般步骤:(1)去分母:各项都乘以分母的最小公倍数;(2)去括号:注意符号问题;(3)移项:移项要变号; (4)合并同类项:系数相加,字母及字母的指数不变; (5)系数化为1:不等式两边同除以未知数的系数.(或同乘以未知数系数的倒数)>><5 >11.若-m>6,则m_______-6.
2.如果 >0, 那么xy______0.
3.如果a>-2,那么a-b_____-2-b.
4.-1.5<-0.3,两边都除以(-0.3),得_______.
5. -3x≤6,两边都除以-3,得_______.x≥2随堂练习6.已知a>b,c>d,求证a-d>b-c.证明:由a>b知a-b>0,由c>d知c-d>0
∵ (a-d)-(b-c)
=(a-b)+(c-d)>0
∴ a-d>b-c7. 解不等式3-x<2x+6并把它的解集表示在
数轴上.解:两边都加上x,得 3<2x+6+x 合并同类项,得 3<3x+6两边都减去6,得 3-6<3x+6-6合并同类项,得 -3<3x两边都除以3,得 -1-1这个不等式的解集在数轴上表示如下图:8. m取何值时,关于x的方程解:解这个方程根据题意,得 解得 m>1的解大于2.9.(1)解不等式 ,并把它的解
在数轴上表示出来.
解 :去分母,得
去括号,得
移项、得
合并同类项,得 3(x-3) ≥2(6+x)
3x-9≥12+2x
3x-2x≥12+9
x≥2110.如果不等式3x-m≤0的正整数解是1、2、3,
则m的取值范围是__________.分析:不等式3x-m≤0的解为:x≤可得: 3 ≤ <4 9≤m<121.3.01,4,6,100是2x+3>9的解,其他数不
是.
2.(1)a+5>0; (2)a-2<0;
(3)b+15<27; (4)b-12>-5;
(5)4c≥8; (6) ≤3;
(7)d+e≥0; (8)d-e≤-2.
3.(1)x> 4; (2)x< 5;
(3)x> 2.1; (4)x>- .习题答案4.(1)a> b→a± c> b± c;
(2)a> b,c> 0 →ac> bc, >
(3)a>b,c<0 →ac<bc, <5.(1)>;(2)>;(3)>;(4)<.
6.(1)x> - 4; (2)x< - 7;
(3)x> - 2; (4)x>-3.
7.(1)>;(2)>.
8.39.98≤L≤40.02.9.设蛋白质的含量为xg,x≥300×0.6%,
x≥1.8.
10.12x+40≤1 000,x≤80.
11.(10a+b) -(10b+a)>0, a>b;
(10a+b) -(10b+a) <0, a<b;
(10a+b) -(10b+a)=0, a=b;12.黄金是质量(克)≥0.9a;白银的质量
(克)≤0.1a.当首饰的质量为定值时,
黄金含量越多,首饰的体积越小.
设首饰的体积为Vcm3,则
13.设李明的冲刺速度为xm/s,则
x>110,x>4.4. 1.理解不等式的性质;
2.会解简单的一元一次不等式,并能在数轴上表示解集.知识与能力教学目标 1.通过类比等式的性质,探索不等式的性质,体会不等式与等式的异同,初步掌握类比的思想方法;
2.通过经历不等式性质的得出过程,积累数学活动经验;
3.通过分组活动探索不等式的性质,体会在解决问题过程中与他人合作的重要性.过程与方法 1.认识通过观察、实验、类比可以获得数学结论,体验数学活动充满着探索性和创造性;
2.在独立思考的基础上,积极参与对数学问题的讨论,敢于发表自己的观点,学会分享别人的想法和结果,并重新审视自己的想法,能从交流中获益.情感态度与价值观掌握不等式的性质.不等式性质3的探索及运用.重点难点教学重难点
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.等式的这些性质适用于不等式吗?不等式有哪些性质呢?新课导入(甲)(乙)100g50g加入20g 加入20g结论:
100>50100+20>50+20 120>70120-20>70-20用“<”或“>”填空,并找一找其中的规律.(2)2<5 , 2+3____5+3 , 2-3____5-3 ;(1)9>6, 9+3____6+3 , 9-3____9-3 ; 当不等式两边加或减去同一个数时,不等号的方向______.不变结论 当不等式的两边同乘同一个负数时,不等号的方向________. (3)8>3, 8×5____3×5 , 8×(-5)____3×(-5) ; (4)1<3, 1×6____3×6 , 1×(-6)____3×(-6). 当不等式的两边同乘同一个正数时,不等号的方向______;不变改变结论不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变. 即 如果a>b,那么a+c>b+c,a-c>b-c.知识要点不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.如果a > b,c > 0那么ac>bc,a/c>b/c.不等式的性质3 不等式两边乘(或除以)
同一个负数,不等号的方向改变.如果 a > b ,c < 0 那么 ac < bc,a/c < b/c.如果a>b,且c>d,那么a+c>b+d . 如果a>b,那么b
(1)x-6>15 (2)4x<3x-2
(3)-2x﹥50 (1)解:为了使不等式x-6>15中不等号的一边变为x,根据不等式的性质1,不等式两边都加6,不等号的方向不变,得
x-6+6﹥15+6,
x﹥21.这个不等式的解集在数轴上的表示如图,4x-3x﹤3x-2-3x
x﹤-2 (2)解 :为了使不等式3x<2x+1中不等号的一边变为x,根据不等式的性质1,不等式两边都减去3x,不等号的方向不变,得这个不等式的解在数轴上的表示如图, (3)解:为了使不等式-2x﹥50中的不等号的一边变为x,根据不等式的性质3,不等式两边都除以-2,不等号的方向改变,得x﹤-25这个不等式的解集在数轴上的表示如图.例2 已知a<0 ,试比较2a与a的大小.解法一:∵2>1,a<0,
∴2a<a(不等式的性质3) 解法二: 在数轴上分别表示2a和a的点(a<0),如图:2a位于a的左边,所以2a<a.解法三:∵ 2a-a=a, 又∵ a<0,
∴ 2a-a<0,
∴2a
x+3 -3<7-3
∴x<4
而满足x<3的正整数有1,2,3,
所以不等式的正整数解为1,2,3.例6 求不等式x+3<7的正整数解.解一元一次不等式的一般步骤:(1)去分母:各项都乘以分母的最小公倍数;(2)去括号:注意符号问题;(3)移项:移项要变号;(4)合并同类项:系数相加,字母及字母的指
数不变; (5)系数化为1:不等式两边同除以未知数的系
数.(或同乘以未知数系数的倒数)解 :去分母,得
去括号,得
移项、得
合并同类项,得
两边都除以5,得 3(x-3) ≥2(8-x)
3x-9≥16-2x
3x+2x≥16+9
5x≥25
x≥5例7 利用不等式的性质解不等式.解:移项得:5x-4x>-4-10合并得x>-14例8 解不等式 5(x+2)>4x-4.去括号得:5x+10>4x-4解:移项得:2x-3x<-9-6合并得:-x<-15例9 解不等式 2(x+3)<3(x-3).去括号得:2x+6<3x-9x>15系数化为1得:例10 解不等式:解:去分母,得
3(2x+1) <2(13x-2) -4(6x+4)
去括号,得
6x+3<26x-4-24x-16
移项,得
6x-26x+24x<-4-16-3
合并,得
4x<-23 例11 当x取何正整数时,代数式 的值比 的值大1?解:根据题意,得 >1,
2(x+5)-3(3x-2)>6,
2x+10-9x+6>6,
-7x+16>6,
-7x>-10,
得 x<
所以,当x=1时,满足题意要求.一元一次不等式ax>b和ax
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1(1)去分母
(2)去括号
(3)移项
(4)合并同类项
(5)系数化为1在(1)与(5)这两步若乘以(或除以)负数,要把不等号方向改变两边同时除以未知数的系数一般只有一个解一般解集含有无数个解一元一次方程与一元一次不等式的解法步骤比较 不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变. 不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变. 不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.课堂小结解一元一次不等式的一般步骤:(1)去分母:各项都乘以分母的最小公倍数;(2)去括号:注意符号问题;(3)移项:移项要变号; (4)合并同类项:系数相加,字母及字母的指数不变; (5)系数化为1:不等式两边同除以未知数的系数.(或同乘以未知数系数的倒数)>><5 >11.若-m>6,则m_______-6.
2.如果 >0, 那么xy______0.
3.如果a>-2,那么a-b_____-2-b.
4.-1.5<-0.3,两边都除以(-0.3),得_______.
5. -3x≤6,两边都除以-3,得_______.x≥2随堂练习6.已知a>b,c>d,求证a-d>b-c.证明:由a>b知a-b>0,由c>d知c-d>0
∵ (a-d)-(b-c)
=(a-b)+(c-d)>0
∴ a-d>b-c7. 解不等式3-x<2x+6并把它的解集表示在
数轴上.解:两边都加上x,得 3<2x+6+x 合并同类项,得 3<3x+6两边都减去6,得 3-6<3x+6-6合并同类项,得 -3<3x两边都除以3,得 -1
在数轴上表示出来.
解 :去分母,得
去括号,得
移项、得
合并同类项,得 3(x-3) ≥2(6+x)
3x-9≥12+2x
3x-2x≥12+9
x≥2110.如果不等式3x-m≤0的正整数解是1、2、3,
则m的取值范围是__________.分析:不等式3x-m≤0的解为:x≤可得: 3 ≤ <4 9≤m<121.3.01,4,6,100是2x+3>9的解,其他数不
是.
2.(1)a+5>0; (2)a-2<0;
(3)b+15<27; (4)b-12>-5;
(5)4c≥8; (6) ≤3;
(7)d+e≥0; (8)d-e≤-2.
3.(1)x> 4; (2)x< 5;
(3)x> 2.1; (4)x>- .习题答案4.(1)a> b→a± c> b± c;
(2)a> b,c> 0 →ac> bc, >
(3)a>b,c<0 →ac<bc, <5.(1)>;(2)>;(3)>;(4)<.
6.(1)x> - 4; (2)x< - 7;
(3)x> - 2; (4)x>-3.
7.(1)>;(2)>.
8.39.98≤L≤40.02.9.设蛋白质的含量为xg,x≥300×0.6%,
x≥1.8.
10.12x+40≤1 000,x≤80.
11.(10a+b) -(10b+a)>0, a>b;
(10a+b) -(10b+a) <0, a<b;
(10a+b) -(10b+a)=0, a=b;12.黄金是质量(克)≥0.9a;白银的质量
(克)≤0.1a.当首饰的质量为定值时,
黄金含量越多,首饰的体积越小.
设首饰的体积为Vcm3,则
13.设李明的冲刺速度为xm/s,则
x>110,x>4.4. 1.理解不等式的性质;
2.会解简单的一元一次不等式,并能在数轴上表示解集.知识与能力教学目标 1.通过类比等式的性质,探索不等式的性质,体会不等式与等式的异同,初步掌握类比的思想方法;
2.通过经历不等式性质的得出过程,积累数学活动经验;
3.通过分组活动探索不等式的性质,体会在解决问题过程中与他人合作的重要性.过程与方法 1.认识通过观察、实验、类比可以获得数学结论,体验数学活动充满着探索性和创造性;
2.在独立思考的基础上,积极参与对数学问题的讨论,敢于发表自己的观点,学会分享别人的想法和结果,并重新审视自己的想法,能从交流中获益.情感态度与价值观掌握不等式的性质.不等式性质3的探索及运用.重点难点教学重难点
