2024年长沙市中考数学一轮模拟卷(二)(含解析)
文档属性
| 名称 | 2024年长沙市中考数学一轮模拟卷(二)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 13:19:49 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024年长沙市中考数学一轮模拟卷(二)
一、单选题
1.下列运动图标中,属于轴对称图形的是( )
A. B.
C. D.
2.国家卫健委通报:截至2021年6月19日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗101000万余剂次,建立免疫屏障,我们一起努力!将数字101000用科学记数法表示为( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.如图,直角三角板的直角顶点放在直线b上,且,则的度数为( )
A. B. C. D.
5.如图,已知,,,,,则点到直线的距离等于( )
A. B. C. D.
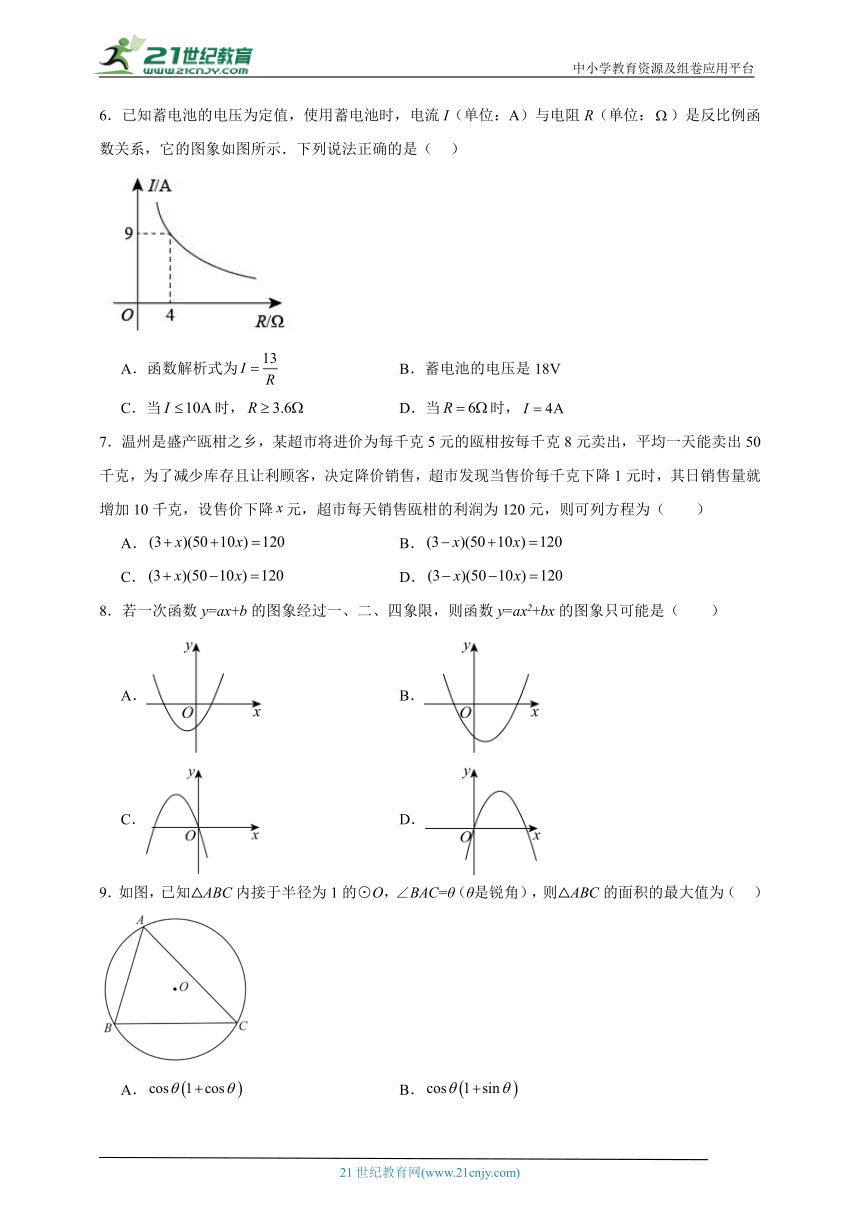
6.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
7.温州是盛产瓯柑之乡,某超市将进价为每千克5元的瓯柑按每千克8元卖出,平均一天能卖出50千克,为了减少库存且让利顾客,决定降价销售,超市发现当售价每千克下降1元时,其日销售量就增加10千克,设售价下降元,超市每天销售瓯柑的利润为120元,则可列方程为( )
A. B.
C. D.
8.若一次函数y=ax+b的图象经过一、二、四象限,则函数y=ax2+bx的图象只可能是( )
A. B.
C. D.
9.如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )
A. B.
C. D.
10.如图,边长为6的等边三角形中,是对称轴上一个动点,连接,将线段绕点逆时针旋转60度得到,连接,则在点运的过程中,最小值是( )
A. B.2 C. D.
二、填空题
11.直线与坐标轴组成的三角形的面积是 .
12.已知一次函数与的图像在y轴上相交于同一点,则 .
13.函数 的自变量x的取值范围是 .
14.已知一次函数,如果y随自变量x的增大而减小,那么m的取值范围为 .
15.一次函数经过点,,则解析式为 .
16.如图,正方形ABCD的对角线AC.BD交于点O,E在BC上,F为DE的中点,△CEF的周长为18,且CE=5,则OF= .
三、解答题
17.计算:.
18.先化简再求值:,其中.
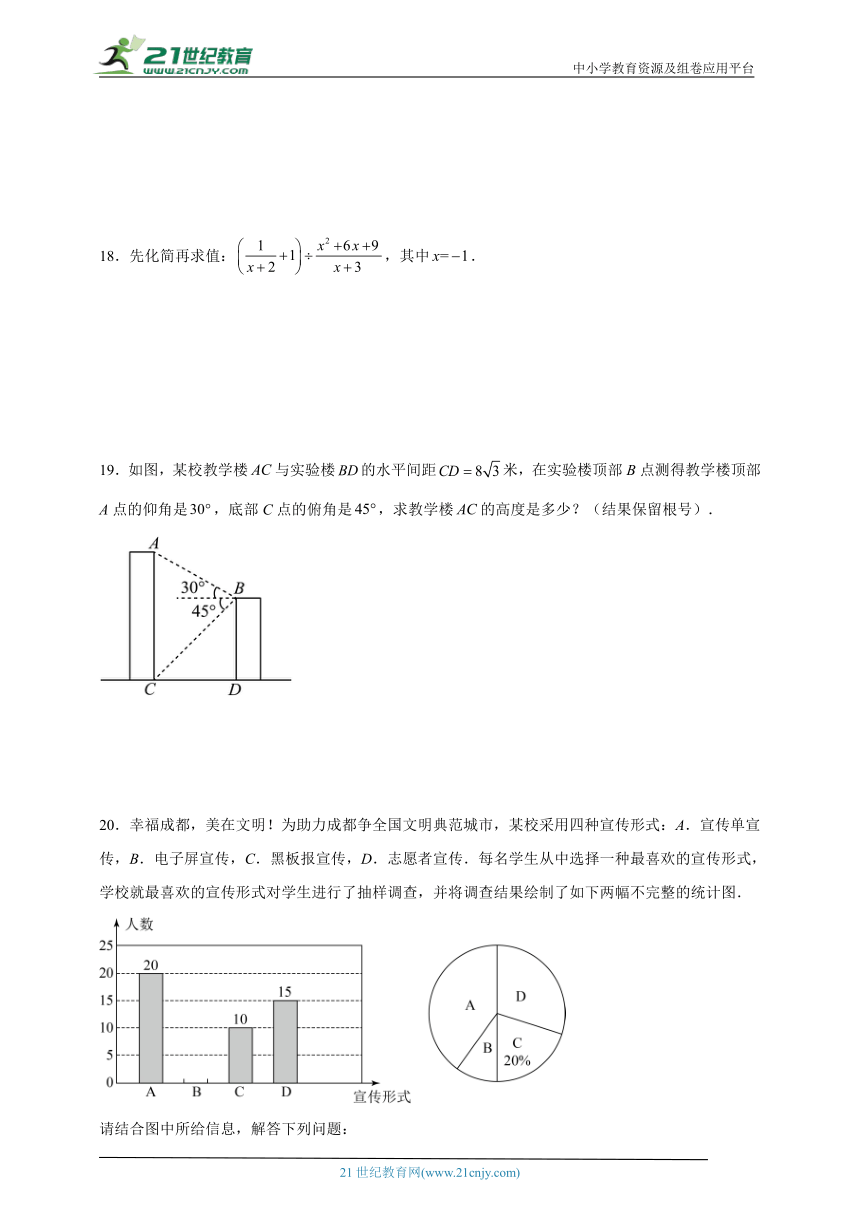
19.如图,某校教学楼与实验楼的水平间距米,在实验楼顶部B点测得教学楼顶部A点的仰角是,底部C点的俯角是,求教学楼的高度是多少?(结果保留根号).
20.幸福成都,美在文明!为助力成都争全国文明典范城市,某校采用四种宣传形式:A.宣传单宣传,B.电子屏宣传,C.黑板报宣传,D.志愿者宣传.每名学生从中选择一种最喜欢的宣传形式,学校就最喜欢的宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.
请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有______人,请补全条形统计图;
(2)扇形统计图中,“D.志愿者宣传”对应的扇形圆心角度数为______;
(3)本次调查中,在最喜欢“志愿者宣传”的学生中,有甲、乙、丙、丁四位同学表现优秀,若从这四位同学中随机选出两名同学参加学校的志愿者活动,请用列表或画树状图的方法,求选出两人恰好是甲和乙的概率
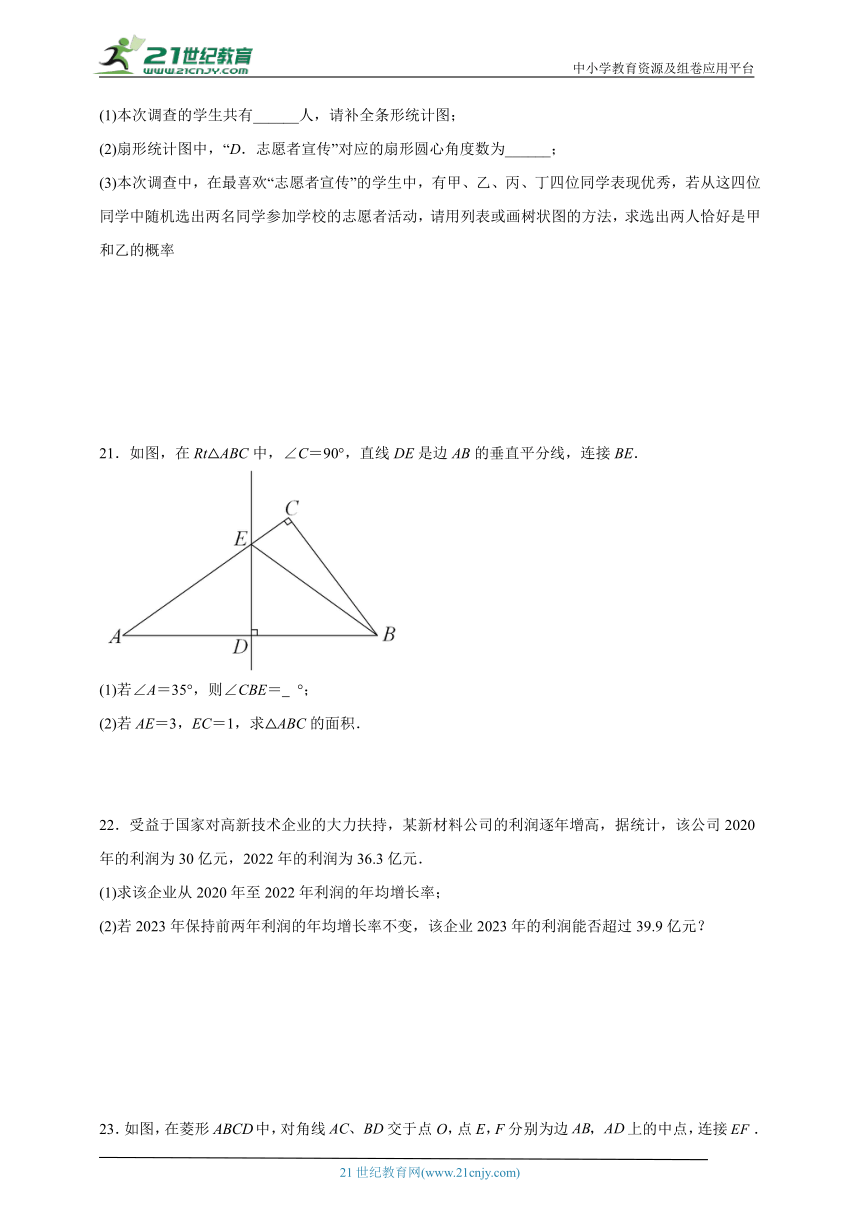
21.如图,在Rt△ABC中,∠C=90°,直线DE是边AB的垂直平分线,连接BE.
(1)若∠A=35°,则∠CBE= °;
(2)若AE=3,EC=1,求△ABC的面积.
22.受益于国家对高新技术企业的大力扶持,某新材料公司的利润逐年增高,据统计,该公司2020年的利润为30亿元,2022年的利润为36.3亿元.
(1)求该企业从2020年至2022年利润的年均增长率;
(2)若2023年保持前两年利润的年均增长率不变,该企业2023年的利润能否超过39.9亿元?
23.如图,在菱形中,对角线交于点O,点E,F分别为边上的中点,连接.
(1)求证:;
(2)若,,求菱形的周长.
24.如图,四边形内接于,对角线交于点E且为直径,延长交于点F,连接,若,请回答下列问题:
(1)求证:;
(2)若,求的值;
(3)设,与四边形的面积之比为h,请求出h关于t的函数关系式.
25.对于以x为自变量的两个函数y与g,令,我们不妨把函数w称之为函数y与g的“辅助函数”例如:以x为白变量的函数与,它们的“辅助函数”为,同时,由于恒成立,所以借助该辅助函数可以证明:不论自变量x取何值,恒成立.
(1)已知以x为白变量的函数与,请求出函数y与g的“辅助函数”,并证明:不论自变量x取何值,恒成立;
(2)已知以x为自变量的函数与,当时,对于x的每一个值,函数y与g的“辅助函数”恒成立,求n的取值范围;
(3)已知以x为自变量的函数与(a、b、c为常数且,),点、、是它们的“辅助函数”w的图象上的三点,且满足,求函数w的图象截x轴得到的线段长度的取值范围.
参考答案:
1.B
【分析】根据轴对称图形的概念逐项分析判断即可,轴对称图形的概念:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.
【详解】A.不是轴对称图形,不符合题意,
B.是轴对称图形,符合题意,
C.不是轴对称图形,不符合题意,
D.不是轴对称图形,不符合题意,
故选:B.
【点睛】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.B
【分析】科学记数法的表示形式为:(其中为整数).确定n的值,要看把原数变为a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n为非负整数;当原数绝对值<1时,n为负整数.
【详解】解:
故选:B.
【点睛】本题考查了科学记数法的表示方法.掌握科学记数法的表示形式(其中为整数)是解题关键.
3.C
【分析】根据合并同类项,平方差公式,幂的乘方,同底数幂的除法逐项分析判断即可.
【详解】解:A. 与不能合并,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项正确,符合题意;
D. ,故该选项不正确,不符合题意;
故选C
【点睛】本题考查了合并同类项,平方差公式,幂的乘方,同底数幂的除法,掌握运算法则是解题的关键.
4.A
【分析】先根据平行线的性质求出的度数,再由两角互余的性质求出的度数即可.
【详解】解:∵,
∴,
∴.
故选:A.
【点睛】本题考查的是平行线的性质,熟知两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等是解题的关键.
5.C
【分析】根据等积法求出点到直线的距离即可.
【详解】解:∵,,
∴,
∴,
即点到直线的距离为,故C正确.
故选:C.
【点睛】本题主要考查了三角形面积计算,点到直线的距离,解题的关键是根据等积法求出.
6.C
【分析】将将代入求出U的值,即可判断A,B,D,利用反比例函数的增减性可判断C.
【详解】解:设,将代入可得,故A错误;
∴蓄电池的电压是36V,故B错误;
当时,,该项正确;
当当时,,故D错误,
故选:C.
【点睛】本题考查反比例函数的实际应用,掌握反比例函数的图象与性质是解题的关键.
7.B
【分析】当售价下降x元时,每千克瓯柑的销售利润为(3-x)元,平均每天的销售量为(50+10x)千克,利用超市每天销售瓯柑获得的利润=每千克的销售利润×平均每天的销售量,即可得出关于x的一元二次方程,此题得解.
【详解】解:当售价下降x元时,每千克瓯柑的销售利润为8-x-5=(3-x)元,
平均每天的销售量为(50+10x)千克,
依题意得:(3-x)(50+10x)=120.
故选:B.
【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
8.D
【分析】根据一次函数y=ax+b的图象位置确定a、b的符号,根据a、b的符号确定二次函数y=ax2+bx图象的位置即可得.
【详解】解:∵一次函数y=ax+b的图象经过一、二、四象限,
∴a<0,b>0,
∴二次函数y=ax2+bx的图象开口向下,
对称轴x=->0,在y轴右边,
∴函数y=ax2+bx的图象只可能是D,
故选D.
【点睛】本题考查了一次函数、二次函数解析式的系数与图象位置的关系.图象的所有性质都与解析式的系数有着密切关系.
9.D
【分析】要使△ABC的面积S=BC h的最大,则h要最大,当高经过圆心时最大.
【详解】解:当△ABC的高AD经过圆的圆心时,此时△ABC的面积最大,
如图所示,
∵A'D⊥BC,
∴BC=2BD,∠BOD=∠BAC=θ,
在Rt△BOD中,
sinθ= ,cosθ=,
∴BD=sinθ,OD=cosθ,
∴BC=2BD=2sinθ,
A'D=A'O+OD=1+cosθ,
∴S△A'BC=AD BC= 2sinθ(1+cosθ)=sinθ(1+cosθ).
故选:D.
【点睛】本题主要考查锐角三角函数的应用与三角形面积的求法.
10.C
【分析】取线段的中点,连接,根据等边三角形的性质以及角的计算即可得出以及,由旋转的性质可得出,由此即可利用全等三角形的判定定理证出,进而即可得出,再根据点为的中点,即可得出的最小值,此题得解.
【详解】解:取线段的中点,连接,如图所示.
为等边三角形,且为的对称轴,
,,
,
.
在和中,
,
,
.
当时,最短,即最短.
点为的中点,
此时.
故选:C.
【点睛】本题考查了等边三角形的性质以及全等三角形的判定与性质,解题的关键是通过全等三角形的性质找出.本题属于中档题,难度不大,解决该题型题目时,根据全等三角形的性质找出相等的边是关键.
11.
【分析】分别令和,可求出与坐标轴的交点,从而可以求解.
【详解】解:当时,;
当时,;
直线与坐标轴的交点分别为:,,
直线与坐标轴所围成的三角形面积:.
故答案为:.
【点睛】本题考查了一次函数与坐标轴交点围成面积问题,掌握与坐标轴交点坐标求法是解题的关键.
12.
【分析】通过已知的一次函数求出其与y轴交点,得到未知函数经过的点,代入求解出参数即可.
【详解】中代入,
得:,
的图像与y轴交点为,
一次函数与的图像在y轴上相交于同一点,
故也经过点,
代入得:,
,
故答案为:.
【点睛】本题考查一次函数交点,能够理清楚函数与函数交点,函数与坐标轴交点的计算方法是解题的关键.
13.
【分析】根据二次根式有意义的条件,列出不等式,即可求解.
【详解】解:根据题意得,,
解得.
故答案为.
【点睛】本题主要考查函数的自变量取值范围,掌握二次根式有意义的条件,是解题的关键.
14./
【分析】利用一次函数中一次项系数正负性与y随自变量x的增大而变化的情况列不等式计算即可.
【详解】y随自变量x的增大而减小,
,
,
故答案为:.
【点睛】题目主要考查一次函数的性质,一次函数中一次项系数,y随自变量x的增大而增大;,y随自变量x的增大而减小.熟悉此函数图像性质是解题的关键.
15.
【分析】根据待定系数法求解函数解析式即可.
【详解】解:把,代入得:
,
解得,
所以一次函数解析式为.
故答案为:.
【点睛】本题主要考查一次函数的解析式,熟练掌握利用待定系数法求解函数解析式是解题的关键.
16.
【分析】取的中点,连接,根据正方形对角线交点是对角线的中点及F为DE的中点可得是的中位线,是的中位线,在根据正方形的性质得,可得和为直角三角形,根据直角三角形斜边的中线性质利用△CEF的周长为18可求出,再利用勾股定理即可求得,则利用中位线的性质即可求解.
【详解】解:取的中点,连接,
正方形ABCD的对角线AC.BD交于点O,且F为DE的中点,
是的中位线,是的中位线,
又四边形是正方形,
,
和为直角三角形,
,
又△CEF的周长为18,且CE=5,
,,
,
,
,
,
,
故答案为.
【点睛】本题考查了三角形中位线性质、直角三角形斜边的中线性质、勾股定理、正方形的性质,解题的关键熟练掌握中位线性质及直角三角形斜边的中线性质.
17.
【分析】原式分别化简,然后再进行加减运算即可得到答案.
【详解】解:
=
=.
【点睛】本题主要考查了实数的混合运算,熟练掌握运算法则是解答本题的关键.
18.;1
【分析】先把分式化简后,再把的值代入求出分式的值即可.
【详解】原式
当时,原式.
【点睛】本题考查了分式的化简求值,熟练分解因式是解题的关键.
19.米
【分析】过点作,垂足为,根据题意可得:,米,然后分别在和中,利用锐角三角函数的定义求出和的长,从而利用线段的和差关系进行计算即可解答.
【详解】解:过点作,垂足为,
由题意得:,米,
在中,,
,即,
解得:米,
在中,,
,即,
解得:米,
米.
【点睛】本题考查了解直角三角形的应用:仰角俯角问题.根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
20.(1)50,图见解析
(2)
(3)
【分析】(1)根据C项目的人数和所占的百分比求出总人数,再用总人数A、C、D项目的人数即可解决问题;
(2)用乘以 “D.志愿者宣传”的学生所占的比例即可;
(3)列出表格,共有12种等可能的情况,其中被选取的两人恰好是甲和乙的有2种情况,再由概率公式求解即可.
【详解】(1)本次调查的学生共有:(人),
喜欢B.电子屏宣传的人数有:(人),
补全条形统计图如图所示:
故答案为:50
(2)“D.志愿者宣传”对应的扇形圆心角度数为;
故答案为:;
(3)列表得:
甲 乙 丙 丁
甲 (甲,乙) (甲,丙) (甲,丁)
乙 (乙,甲) (乙,丙) (乙,丁)
丙 (丙,甲) (丙,乙) (丙,丁)
丁 (丁,甲) (丁,乙) (丁,丙)
共有12种等可能的结果,其中恰好是甲和乙的有2种,
∴被选取的两人恰好是甲和乙的概率是.
【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.也考查了统计图.
21.(1)20;
(2)
【分析】(1)根据直角三角形的性质求出∠ABC,根据线段垂直平分线的性质得到EA=EB,进而得到∠EBA=∠A=35°,计算即可;
(2)根据勾股定理求出BC,根据三角形的面积公式计算,得到答案.
【详解】(1)解:∵∠C=90°,∠A=35°,
∴∠ABC=90°﹣35°=55°,
∵DE是线段AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=35°,
∴∠CBE=∠ABC﹣EBA=55°﹣35°=20°,
故答案为:20;
(2)解:∵EB=EA=3,EC=1,
∴BC= ,AC=AE+EC=4,
∴△ABC的面积=×AC×BC=4.
【点睛】本题考查的是线段垂直平分线的性质、三角形的面积计算,掌握垂直平分线上任意一点到线段两端点的距离相等是解题的关键.
22.(1)10%
(2)能
【分析】(1)设年均增长率为x,根据“公司2020年的利润为30亿元,2022年的利润为36.3亿元”列方程求解即可;
(2)根据(1)中的增长率求出2023年的利润,再与39.9亿元比较即可.
【详解】(1)设该公司从2020年至2022年利润的年均增长率为x,
根据题意得:,
解得:,(不符合题意,舍去).
答:该企业从2020年至2022年利润的年均增长率为10%.
(2)(亿元)
∴该企业2023年的利润能超过39.9亿元.
【点睛】本题考查一元二次方程的应用,读懂题意,正确列出方程是解题的关键.
23.(1)见解析
(2)
【分析】(1)根据菱形的性质以及三角形中位线的性质,求证即可;
(2)根据中位线的性质,求得,再根据三角函数求得,勾股定理求得,即可求解.
【详解】(1)证明:∵四边形为菱形,
∴,
∵点为中点,
∴,
∴;
(2)解:点为中点,
∴,
∴
∵四边形为菱形
∴
在中,
∴,
由勾股定理得:
∴菱形的周长为
【点睛】此题主要考查了菱形的性质,三角形中位线的性质,勾股定理,解题的关键是熟练掌握相关基础性质.
24.(1)见解析
(2)
(3)
【分析】(1)根据同弧所对圆周角相等得,结合可证明结论;
(2)设,则,,由,可得再证明即可得出结论;
(3)证明得即设的半径为,则证明可得出进一步可得出答案.
【详解】(1)∵,
∴,
又∵
∴;
(2)由(1)知,,
∴
∵
∴
∴
∵
∴
∴
∵,
∵设,则,,
由(1),
∴
∴
∵
∴
∴
∴
(3)∵四边形内接于,
∴
又
∴
∵
∴
∵与四边形的面积之比为h,
设四边形的面积为,则
∴
∴
∴
设的半径为,则
∵,
∴
∴
∵
∴
∴
∵
∴
∴即
∴
∵
∴
∴
∴
∴.
【点睛】本题主要考查了圆周角定理,圆内接四边形的性质,相似三角形的判定与性质等知识,灵活判定三角形相似是解答本题的关键.
25.(1)见解析
(2)
(3)且
【分析】(1)直接根据辅助函数的定义,可得,即可求解;
(2)直接根据辅助函数的定义,可得辅助函数,再由当时,对于x的每一个值,函数y与g的“辅助函数”恒成立,可得恒成立,即可求解;
(3)直接根据辅助函数的定义,可得辅助函数,再把点、、代入可得,,再由,可得且,不妨令,则,利用根与系数的关系可得函数w与x轴交于,则是方程的两根,从而得到的值,即可求解.
【详解】(1)解:函数与,
∴辅助函数,
∵,
∴恒成立,即恒成立;
(2)解:∵函数与,
∴辅助函数,
∵当时,对于x的每一个值,函数y与g的“辅助函数”恒成立,
∴恒成立,
当时,,
当时,恒成立,
所以;
(3)解:∵函数与,
∴,
将点、、代入解析式得:
,,
∴,
∵,
∴,
解不等式得:且,
不妨令,则,
设函数w与x轴交于,
所以是方程的两根,
∴,,
∴
∵,
∴且,
即且.
【点睛】本题主要考查了二次函数的综合题,理解新函数的定义,熟练掌握二次函数的图象和性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024年长沙市中考数学一轮模拟卷(二)
一、单选题
1.下列运动图标中,属于轴对称图形的是( )
A. B.
C. D.
2.国家卫健委通报:截至2021年6月19日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗101000万余剂次,建立免疫屏障,我们一起努力!将数字101000用科学记数法表示为( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.如图,直角三角板的直角顶点放在直线b上,且,则的度数为( )
A. B. C. D.
5.如图,已知,,,,,则点到直线的距离等于( )
A. B. C. D.
6.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当时,
7.温州是盛产瓯柑之乡,某超市将进价为每千克5元的瓯柑按每千克8元卖出,平均一天能卖出50千克,为了减少库存且让利顾客,决定降价销售,超市发现当售价每千克下降1元时,其日销售量就增加10千克,设售价下降元,超市每天销售瓯柑的利润为120元,则可列方程为( )
A. B.
C. D.
8.若一次函数y=ax+b的图象经过一、二、四象限,则函数y=ax2+bx的图象只可能是( )
A. B.
C. D.
9.如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )
A. B.
C. D.
10.如图,边长为6的等边三角形中,是对称轴上一个动点,连接,将线段绕点逆时针旋转60度得到,连接,则在点运的过程中,最小值是( )
A. B.2 C. D.
二、填空题
11.直线与坐标轴组成的三角形的面积是 .
12.已知一次函数与的图像在y轴上相交于同一点,则 .
13.函数 的自变量x的取值范围是 .
14.已知一次函数,如果y随自变量x的增大而减小,那么m的取值范围为 .
15.一次函数经过点,,则解析式为 .
16.如图,正方形ABCD的对角线AC.BD交于点O,E在BC上,F为DE的中点,△CEF的周长为18,且CE=5,则OF= .
三、解答题
17.计算:.
18.先化简再求值:,其中.
19.如图,某校教学楼与实验楼的水平间距米,在实验楼顶部B点测得教学楼顶部A点的仰角是,底部C点的俯角是,求教学楼的高度是多少?(结果保留根号).
20.幸福成都,美在文明!为助力成都争全国文明典范城市,某校采用四种宣传形式:A.宣传单宣传,B.电子屏宣传,C.黑板报宣传,D.志愿者宣传.每名学生从中选择一种最喜欢的宣传形式,学校就最喜欢的宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.
请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有______人,请补全条形统计图;
(2)扇形统计图中,“D.志愿者宣传”对应的扇形圆心角度数为______;
(3)本次调查中,在最喜欢“志愿者宣传”的学生中,有甲、乙、丙、丁四位同学表现优秀,若从这四位同学中随机选出两名同学参加学校的志愿者活动,请用列表或画树状图的方法,求选出两人恰好是甲和乙的概率
21.如图,在Rt△ABC中,∠C=90°,直线DE是边AB的垂直平分线,连接BE.
(1)若∠A=35°,则∠CBE= °;
(2)若AE=3,EC=1,求△ABC的面积.
22.受益于国家对高新技术企业的大力扶持,某新材料公司的利润逐年增高,据统计,该公司2020年的利润为30亿元,2022年的利润为36.3亿元.
(1)求该企业从2020年至2022年利润的年均增长率;
(2)若2023年保持前两年利润的年均增长率不变,该企业2023年的利润能否超过39.9亿元?
23.如图,在菱形中,对角线交于点O,点E,F分别为边上的中点,连接.
(1)求证:;
(2)若,,求菱形的周长.
24.如图,四边形内接于,对角线交于点E且为直径,延长交于点F,连接,若,请回答下列问题:
(1)求证:;
(2)若,求的值;
(3)设,与四边形的面积之比为h,请求出h关于t的函数关系式.
25.对于以x为自变量的两个函数y与g,令,我们不妨把函数w称之为函数y与g的“辅助函数”例如:以x为白变量的函数与,它们的“辅助函数”为,同时,由于恒成立,所以借助该辅助函数可以证明:不论自变量x取何值,恒成立.
(1)已知以x为白变量的函数与,请求出函数y与g的“辅助函数”,并证明:不论自变量x取何值,恒成立;
(2)已知以x为自变量的函数与,当时,对于x的每一个值,函数y与g的“辅助函数”恒成立,求n的取值范围;
(3)已知以x为自变量的函数与(a、b、c为常数且,),点、、是它们的“辅助函数”w的图象上的三点,且满足,求函数w的图象截x轴得到的线段长度的取值范围.
参考答案:
1.B
【分析】根据轴对称图形的概念逐项分析判断即可,轴对称图形的概念:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形.
【详解】A.不是轴对称图形,不符合题意,
B.是轴对称图形,符合题意,
C.不是轴对称图形,不符合题意,
D.不是轴对称图形,不符合题意,
故选:B.
【点睛】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.B
【分析】科学记数法的表示形式为:(其中为整数).确定n的值,要看把原数变为a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n为非负整数;当原数绝对值<1时,n为负整数.
【详解】解:
故选:B.
【点睛】本题考查了科学记数法的表示方法.掌握科学记数法的表示形式(其中为整数)是解题关键.
3.C
【分析】根据合并同类项,平方差公式,幂的乘方,同底数幂的除法逐项分析判断即可.
【详解】解:A. 与不能合并,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项正确,符合题意;
D. ,故该选项不正确,不符合题意;
故选C
【点睛】本题考查了合并同类项,平方差公式,幂的乘方,同底数幂的除法,掌握运算法则是解题的关键.
4.A
【分析】先根据平行线的性质求出的度数,再由两角互余的性质求出的度数即可.
【详解】解:∵,
∴,
∴.
故选:A.
【点睛】本题考查的是平行线的性质,熟知两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等是解题的关键.
5.C
【分析】根据等积法求出点到直线的距离即可.
【详解】解:∵,,
∴,
∴,
即点到直线的距离为,故C正确.
故选:C.
【点睛】本题主要考查了三角形面积计算,点到直线的距离,解题的关键是根据等积法求出.
6.C
【分析】将将代入求出U的值,即可判断A,B,D,利用反比例函数的增减性可判断C.
【详解】解:设,将代入可得,故A错误;
∴蓄电池的电压是36V,故B错误;
当时,,该项正确;
当当时,,故D错误,
故选:C.
【点睛】本题考查反比例函数的实际应用,掌握反比例函数的图象与性质是解题的关键.
7.B
【分析】当售价下降x元时,每千克瓯柑的销售利润为(3-x)元,平均每天的销售量为(50+10x)千克,利用超市每天销售瓯柑获得的利润=每千克的销售利润×平均每天的销售量,即可得出关于x的一元二次方程,此题得解.
【详解】解:当售价下降x元时,每千克瓯柑的销售利润为8-x-5=(3-x)元,
平均每天的销售量为(50+10x)千克,
依题意得:(3-x)(50+10x)=120.
故选:B.
【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
8.D
【分析】根据一次函数y=ax+b的图象位置确定a、b的符号,根据a、b的符号确定二次函数y=ax2+bx图象的位置即可得.
【详解】解:∵一次函数y=ax+b的图象经过一、二、四象限,
∴a<0,b>0,
∴二次函数y=ax2+bx的图象开口向下,
对称轴x=->0,在y轴右边,
∴函数y=ax2+bx的图象只可能是D,
故选D.
【点睛】本题考查了一次函数、二次函数解析式的系数与图象位置的关系.图象的所有性质都与解析式的系数有着密切关系.
9.D
【分析】要使△ABC的面积S=BC h的最大,则h要最大,当高经过圆心时最大.
【详解】解:当△ABC的高AD经过圆的圆心时,此时△ABC的面积最大,
如图所示,
∵A'D⊥BC,
∴BC=2BD,∠BOD=∠BAC=θ,
在Rt△BOD中,
sinθ= ,cosθ=,
∴BD=sinθ,OD=cosθ,
∴BC=2BD=2sinθ,
A'D=A'O+OD=1+cosθ,
∴S△A'BC=AD BC= 2sinθ(1+cosθ)=sinθ(1+cosθ).
故选:D.
【点睛】本题主要考查锐角三角函数的应用与三角形面积的求法.
10.C
【分析】取线段的中点,连接,根据等边三角形的性质以及角的计算即可得出以及,由旋转的性质可得出,由此即可利用全等三角形的判定定理证出,进而即可得出,再根据点为的中点,即可得出的最小值,此题得解.
【详解】解:取线段的中点,连接,如图所示.
为等边三角形,且为的对称轴,
,,
,
.
在和中,
,
,
.
当时,最短,即最短.
点为的中点,
此时.
故选:C.
【点睛】本题考查了等边三角形的性质以及全等三角形的判定与性质,解题的关键是通过全等三角形的性质找出.本题属于中档题,难度不大,解决该题型题目时,根据全等三角形的性质找出相等的边是关键.
11.
【分析】分别令和,可求出与坐标轴的交点,从而可以求解.
【详解】解:当时,;
当时,;
直线与坐标轴的交点分别为:,,
直线与坐标轴所围成的三角形面积:.
故答案为:.
【点睛】本题考查了一次函数与坐标轴交点围成面积问题,掌握与坐标轴交点坐标求法是解题的关键.
12.
【分析】通过已知的一次函数求出其与y轴交点,得到未知函数经过的点,代入求解出参数即可.
【详解】中代入,
得:,
的图像与y轴交点为,
一次函数与的图像在y轴上相交于同一点,
故也经过点,
代入得:,
,
故答案为:.
【点睛】本题考查一次函数交点,能够理清楚函数与函数交点,函数与坐标轴交点的计算方法是解题的关键.
13.
【分析】根据二次根式有意义的条件,列出不等式,即可求解.
【详解】解:根据题意得,,
解得.
故答案为.
【点睛】本题主要考查函数的自变量取值范围,掌握二次根式有意义的条件,是解题的关键.
14./
【分析】利用一次函数中一次项系数正负性与y随自变量x的增大而变化的情况列不等式计算即可.
【详解】y随自变量x的增大而减小,
,
,
故答案为:.
【点睛】题目主要考查一次函数的性质,一次函数中一次项系数,y随自变量x的增大而增大;,y随自变量x的增大而减小.熟悉此函数图像性质是解题的关键.
15.
【分析】根据待定系数法求解函数解析式即可.
【详解】解:把,代入得:
,
解得,
所以一次函数解析式为.
故答案为:.
【点睛】本题主要考查一次函数的解析式,熟练掌握利用待定系数法求解函数解析式是解题的关键.
16.
【分析】取的中点,连接,根据正方形对角线交点是对角线的中点及F为DE的中点可得是的中位线,是的中位线,在根据正方形的性质得,可得和为直角三角形,根据直角三角形斜边的中线性质利用△CEF的周长为18可求出,再利用勾股定理即可求得,则利用中位线的性质即可求解.
【详解】解:取的中点,连接,
正方形ABCD的对角线AC.BD交于点O,且F为DE的中点,
是的中位线,是的中位线,
又四边形是正方形,
,
和为直角三角形,
,
又△CEF的周长为18,且CE=5,
,,
,
,
,
,
,
故答案为.
【点睛】本题考查了三角形中位线性质、直角三角形斜边的中线性质、勾股定理、正方形的性质,解题的关键熟练掌握中位线性质及直角三角形斜边的中线性质.
17.
【分析】原式分别化简,然后再进行加减运算即可得到答案.
【详解】解:
=
=.
【点睛】本题主要考查了实数的混合运算,熟练掌握运算法则是解答本题的关键.
18.;1
【分析】先把分式化简后,再把的值代入求出分式的值即可.
【详解】原式
当时,原式.
【点睛】本题考查了分式的化简求值,熟练分解因式是解题的关键.
19.米
【分析】过点作,垂足为,根据题意可得:,米,然后分别在和中,利用锐角三角函数的定义求出和的长,从而利用线段的和差关系进行计算即可解答.
【详解】解:过点作,垂足为,
由题意得:,米,
在中,,
,即,
解得:米,
在中,,
,即,
解得:米,
米.
【点睛】本题考查了解直角三角形的应用:仰角俯角问题.根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
20.(1)50,图见解析
(2)
(3)
【分析】(1)根据C项目的人数和所占的百分比求出总人数,再用总人数A、C、D项目的人数即可解决问题;
(2)用乘以 “D.志愿者宣传”的学生所占的比例即可;
(3)列出表格,共有12种等可能的情况,其中被选取的两人恰好是甲和乙的有2种情况,再由概率公式求解即可.
【详解】(1)本次调查的学生共有:(人),
喜欢B.电子屏宣传的人数有:(人),
补全条形统计图如图所示:
故答案为:50
(2)“D.志愿者宣传”对应的扇形圆心角度数为;
故答案为:;
(3)列表得:
甲 乙 丙 丁
甲 (甲,乙) (甲,丙) (甲,丁)
乙 (乙,甲) (乙,丙) (乙,丁)
丙 (丙,甲) (丙,乙) (丙,丁)
丁 (丁,甲) (丁,乙) (丁,丙)
共有12种等可能的结果,其中恰好是甲和乙的有2种,
∴被选取的两人恰好是甲和乙的概率是.
【点睛】本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.也考查了统计图.
21.(1)20;
(2)
【分析】(1)根据直角三角形的性质求出∠ABC,根据线段垂直平分线的性质得到EA=EB,进而得到∠EBA=∠A=35°,计算即可;
(2)根据勾股定理求出BC,根据三角形的面积公式计算,得到答案.
【详解】(1)解:∵∠C=90°,∠A=35°,
∴∠ABC=90°﹣35°=55°,
∵DE是线段AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=35°,
∴∠CBE=∠ABC﹣EBA=55°﹣35°=20°,
故答案为:20;
(2)解:∵EB=EA=3,EC=1,
∴BC= ,AC=AE+EC=4,
∴△ABC的面积=×AC×BC=4.
【点睛】本题考查的是线段垂直平分线的性质、三角形的面积计算,掌握垂直平分线上任意一点到线段两端点的距离相等是解题的关键.
22.(1)10%
(2)能
【分析】(1)设年均增长率为x,根据“公司2020年的利润为30亿元,2022年的利润为36.3亿元”列方程求解即可;
(2)根据(1)中的增长率求出2023年的利润,再与39.9亿元比较即可.
【详解】(1)设该公司从2020年至2022年利润的年均增长率为x,
根据题意得:,
解得:,(不符合题意,舍去).
答:该企业从2020年至2022年利润的年均增长率为10%.
(2)(亿元)
∴该企业2023年的利润能超过39.9亿元.
【点睛】本题考查一元二次方程的应用,读懂题意,正确列出方程是解题的关键.
23.(1)见解析
(2)
【分析】(1)根据菱形的性质以及三角形中位线的性质,求证即可;
(2)根据中位线的性质,求得,再根据三角函数求得,勾股定理求得,即可求解.
【详解】(1)证明:∵四边形为菱形,
∴,
∵点为中点,
∴,
∴;
(2)解:点为中点,
∴,
∴
∵四边形为菱形
∴
在中,
∴,
由勾股定理得:
∴菱形的周长为
【点睛】此题主要考查了菱形的性质,三角形中位线的性质,勾股定理,解题的关键是熟练掌握相关基础性质.
24.(1)见解析
(2)
(3)
【分析】(1)根据同弧所对圆周角相等得,结合可证明结论;
(2)设,则,,由,可得再证明即可得出结论;
(3)证明得即设的半径为,则证明可得出进一步可得出答案.
【详解】(1)∵,
∴,
又∵
∴;
(2)由(1)知,,
∴
∵
∴
∴
∵
∴
∴
∵,
∵设,则,,
由(1),
∴
∴
∵
∴
∴
∴
(3)∵四边形内接于,
∴
又
∴
∵
∴
∵与四边形的面积之比为h,
设四边形的面积为,则
∴
∴
∴
设的半径为,则
∵,
∴
∴
∵
∴
∴
∵
∴
∴即
∴
∵
∴
∴
∴
∴.
【点睛】本题主要考查了圆周角定理,圆内接四边形的性质,相似三角形的判定与性质等知识,灵活判定三角形相似是解答本题的关键.
25.(1)见解析
(2)
(3)且
【分析】(1)直接根据辅助函数的定义,可得,即可求解;
(2)直接根据辅助函数的定义,可得辅助函数,再由当时,对于x的每一个值,函数y与g的“辅助函数”恒成立,可得恒成立,即可求解;
(3)直接根据辅助函数的定义,可得辅助函数,再把点、、代入可得,,再由,可得且,不妨令,则,利用根与系数的关系可得函数w与x轴交于,则是方程的两根,从而得到的值,即可求解.
【详解】(1)解:函数与,
∴辅助函数,
∵,
∴恒成立,即恒成立;
(2)解:∵函数与,
∴辅助函数,
∵当时,对于x的每一个值,函数y与g的“辅助函数”恒成立,
∴恒成立,
当时,,
当时,恒成立,
所以;
(3)解:∵函数与,
∴,
将点、、代入解析式得:
,,
∴,
∵,
∴,
解不等式得:且,
不妨令,则,
设函数w与x轴交于,
所以是方程的两根,
∴,,
∴
∵,
∴且,
即且.
【点睛】本题主要考查了二次函数的综合题,理解新函数的定义,熟练掌握二次函数的图象和性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
