2024年深圳市中考数学一轮模拟卷(二)(含解析)
文档属性
| 名称 | 2024年深圳市中考数学一轮模拟卷(二)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024年深圳市中考数学一轮模拟卷(二)
一、单选题
1.下列实数中,最大的数是( )
A. B. C. D.3
2.今年是中国共产党建党100周年,过去的100年是奋斗的100年,中国在各个方面都取得了巨大的成就.2020年GDP同比增长2.3%,GDP总量达到约102万亿元,其中102万用科学记数法表示为( )
A.10.2×105 B.1.02×106 C.1.02×105 D.10.2×104
3.在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
A.6个 B.15个 C.13个 D.12个
4.不等式组的解集是( )
A.x>2 B.﹣3<x<2 C.﹣1<x<2 D.﹣2<x<2
5.关于数据3,,,0,5的说法正确的是( )
A.平均数为 B.中位数为1 C.众数为5 D.方差为6.8
6.关于一元二次方程根的情况,下列说法中正确的是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
7.如图,火车匀速通过隧道(隧道长等于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图像描述大致是( )
A. B.
C. D.
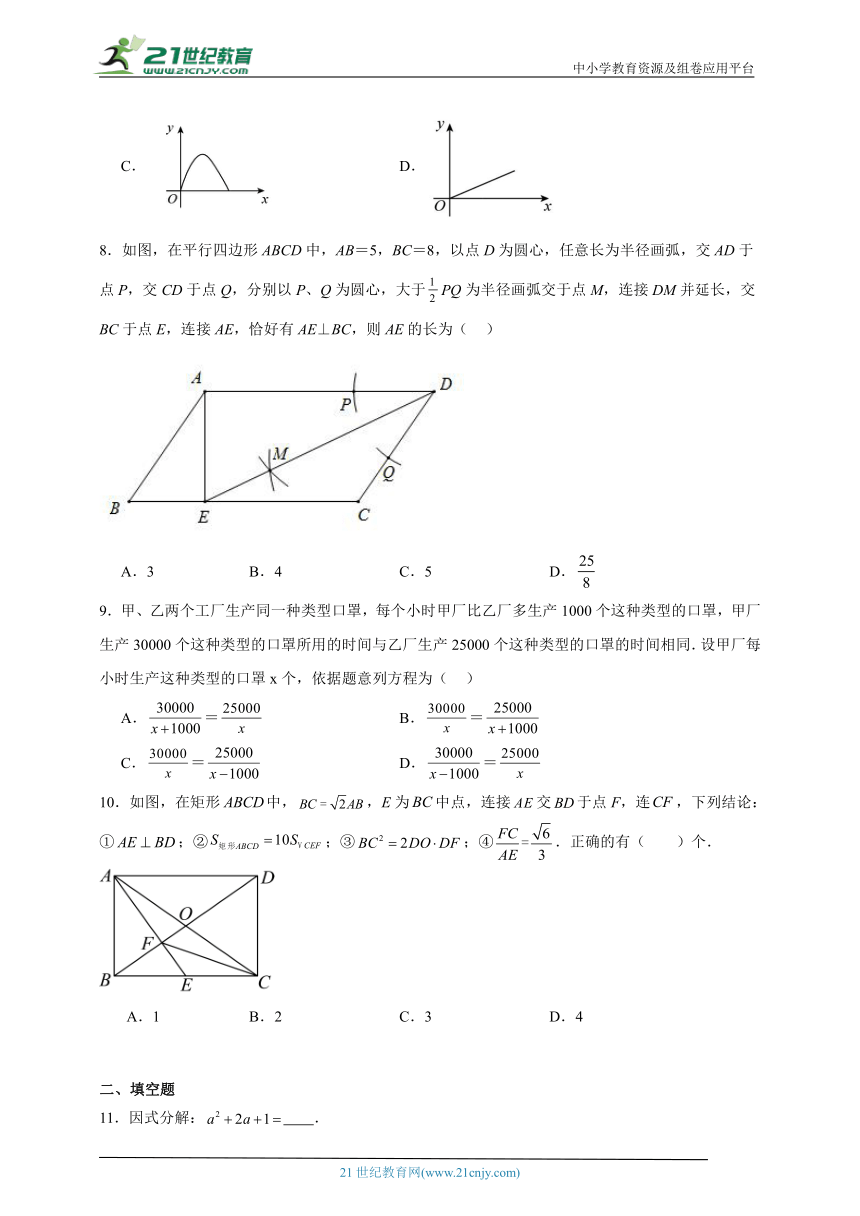
8.如图,在平行四边形ABCD中,AB=5,BC=8,以点D为圆心,任意长为半径画弧,交AD于点P,交CD于点Q,分别以P、Q为圆心,大于PQ为半径画弧交于点M,连接DM并延长,交BC于点E,连接AE,恰好有AE⊥BC,则AE的长为( )
A.3 B.4 C.5 D.
9.甲、乙两个工厂生产同一种类型口罩,每个小时甲厂比乙厂多生产1000个这种类型的口罩,甲厂生产30000个这种类型的口罩所用的时间与乙厂生产25000个这种类型的口罩的时间相同.设甲厂每小时生产这种类型的口罩x个,依据题意列方程为( )
A.= B.=
C.= D.=
10.如图,在矩形中,,E为中点,连接交于点F,连,下列结论:①;②;③;④.正确的有( )个.
A.1 B.2 C.3 D.4
二、填空题
11.因式分解: .
12.假期前,小明家设计了3种度假方案:参观动植物园、看电影、近郊露营.妈妈将三种方案分别写在3张相同的卡片上,小明随机抽取1张,他抽到去近郊露营的概率是 .
13.已知关于x的一元二次方程的一个根为1,则m= .
14.如图,直线y=﹣2x+4与x轴,y轴分别相交于点A、B,四边形ABCD是正方形,双曲线在第一象限经过点D,将正方形向下平移m个单位后,点C刚好落在双曲线上,则m= .
15.如图,已知在中,,,点D在边上,连接.以为斜边作,且,边的中点F恰好落在边上.若,则 .
三、解答题
16.计算:.
17.先化简,再求值:,其中.
18.济南某中学全校学生参加了“庆祝中国共青团成立100周年”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:分以下(不包括70);;;,并绘制出不完整的统计图.
(1)被抽取的学生成绩在C组的有______人,请补全条形统计图;
(2)被抽取的学生成绩在A组的对应扇形圆心角的度数是______度;
(3)若该中学全校共有2400人,则成绩在B组的大约有多少人?
19.飞盘运动由于门槛低、限制少,且具有较强的团体性和趣味性,在全国各地悄然兴起,深受年轻人喜爱,某商家拟用620元购进30个海绵飞盘和50个橡胶飞盘,已知橡胶飞盘的进货单价比海绵飞盘的进价单价多6元.
(1)海绵飞盘和橡胶飞盘的进货单价分别是多少元
(2)由于飞盘畅销,商家决定再购进这两种飞盘共300个,其中橡胶飞盘数量不多于海绵飞盘数量的2倍,且每种飞盘的进货单价保持不变,若橡胶飞盘的销售单价为14元,海绵的销售单价为6元,试问第二批购进橡胶飞盘多少个时,全部售完后,第二批飞盘获得利润最大?第二批飞盘的最大利润是多少元?
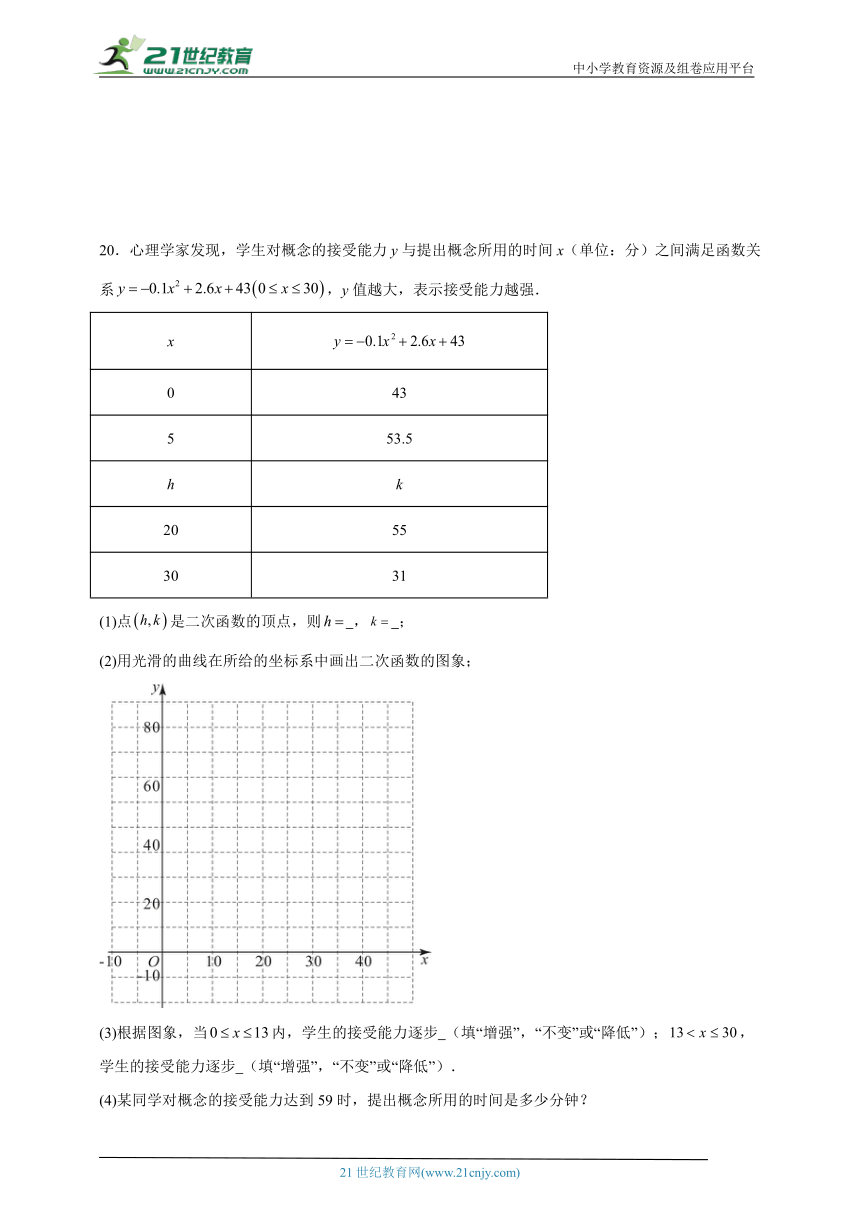
20.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间满足函数关系,y值越大,表示接受能力越强.
x
0 43
5 53.5
h k
20 55
30 31
(1)点是二次函数的顶点,则 , ;
(2)用光滑的曲线在所给的坐标系中画出二次函数的图象;
(3)根据图象,当内,学生的接受能力逐步 (填“增强”,“不变”或“降低”);,学生的接受能力逐步 (填“增强”,“不变”或“降低”).
(4)某同学对概念的接受能力达到59时,提出概念所用的时间是多少分钟?
21.综合与实践
问题情境:在中,,,.直角三角板中,将三角板的直角顶点放在斜边的中点处,并将三角板绕点旋转,三角板的两边,分别与边,交于点M,N.
猜想证明:
(1)如图①,在三角板旋转过程中,当点M为边的中点时,试判断四边形的形状,并说明理由;
问题解决:
(2)如图②,在三角板旋转过程中,当时,请直接写出的长;
(3)如图③,在三角板旋转过程中,当时,请求出线段的长.
22.(1)【探究发现】如图1,正方形的对角线相交于点O,在正方形绕点O旋转的过程中,边与边交于点M,边与边交于点N.证明: ;
(2)【类比迁移】如图2,矩形的对角线相交于点O,且,,在矩形,绕点O旋转的过程中,边与边交于点M,边与边交于点N.若,求的长;
(3)【拓展应用】如图3,四边形和四边形都是平行四边形,且,,,是直角三角形,在绕点O旋转的过程中,边与边交于点M,边与边交于点N.当与重叠部分的面积是的面积的时,请直接写出的长.
参考答案:
1.A
【分析】直接根据实数的大小比较法则比较数的大小即可.
【详解】解:,,,
∴,
故选:A.
【点睛】本题考查了实数的大小比较,关键要熟记:正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小.
2.B
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.
【详解】解:102万=1020000=1.02×106.
故选:B.
【点睛】此题主要考查了用科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|<10,确定a与n的值是解题的关键.
3.D
【详解】解:设白球个数为:x个,
∵摸到红色球的频率稳定在25%左右,∴口袋中得到红色球的概率为25%.
∴,解得:x=12.
经检验:x=12是原方程的解
∴白球的个数为12个.
故选D.
4.D
【分析】先求出两个不等式的解集,然后再写出不等式组的解集即可.
【详解】,
解①得:x>﹣2,
解②得:x<2,
故不等式组的解集是:﹣2<x<2,故D正确.
故选:D.
【点睛】本题主要考查了解一元一次不等式组,正确解出两个不等式的解集,是解题的关键.
5.D
【分析】根据平均数,中位数,众数和方差的求法逐一进行判断即可.
【详解】A,平均数为 ,故该选项错误;
B,中位数为0,故该选项错误;
C,所有数据都是出现了1次,所以这组数据没有众数;
D,方差为,故该选项正确;
故选:D.
【点睛】本题主要考查数据分析,掌握平均数,中位数,众数和方差的求法是解题的关键.
6.A
【分析】直接利用一元二次方程根的判别式即可得.
【详解】解:
其中,,,
∴,
∴方程有两个不相等的实数根.
故选:A.
【点睛】本题考查了一元二次方程根的判别式,熟练掌握一元二次方程根的判别式是解题关键.
7.B
【详解】解:根据题意可知火车进入隧道的时间x与火车在隧道内的长度y之间的关系具体可描述为:
当火车开始进入时y逐渐变大,当火车完全进入隧道,由于隧道长等于火车长,此时y最大,当火车开始出来时y逐渐变小.另外是匀速运动,y随x的均匀变化而均匀变化,故图象呈直线型,排除选项C.
故选:B.
8.B
【分析】由题意可知,再利用平行四边形的性质即可证明,即,即可求出,最后在中,利用勾股定理即可求出AE的长.
【详解】根据作图可知DE为的角平分线,即,
∵四边形ABCD为平行四边形,
∴,
∴,
∴,
∴,
∴,
∴在中,.
故选B.
【点睛】本题考查角平分线的判定和性质,平行四边形的性质,等腰三角形的判定和性质以及勾股定理.理解题意,判断出DE为的角平分线是解答本题的关键.
9.C
【分析】直接利用甲厂生产30000个和乙厂生产25000个口罩的时间相同得出等式即可.
【详解】解:设甲厂每小时生产这种类型的口罩个,依据题意列方程为:
.
故选:C.
【点睛】本题考查了根据实际问题列分式方程,找到等量关系是解题的关键.
10.C
【分析】利用矩形的性质,勾股定理及相似三角形的判定与性质即可解答.
【详解】解:①为中点,
,
,
,
,
,
,
,
,
,故①正确;
②过点作于点,如图,
设,则,,
,,
,
,
设,则,
在中,,
即,
解得:,
,
在中,由勾股定理得,
,
即,
,
,
,
故,故②错误;
③,,
,
,
,
,
,,
,故③正确;
④如图,
在,由勾股定理得,
,,
在,由勾股定理得,
,
在,由勾股定理得,
,故④正确;
故选:C.
【点睛】本题考查了矩形的性质,勾股定理的运用,相似三角形的性质等知识,关键能运用这些知识表示出需要的边或角,即可解决.
11..
【分析】直接运用完全平方公式进行分解即可.
【详解】解:.
故答案为:
【点睛】本题考查了因式分解,掌握完全平方公式是解题关键.
12.
【分析】直接根据概率公式求解即可.
【详解】解:∵妈妈将三种方案分别写在3张相同的卡片上,即共有3种等可能结果,
∴小明随机抽取1张,他抽到去近郊露营的概率是.
故答案为:.
【点睛】本题考查了概率,熟练掌握概率公式是解本题的关键.概率等于所求情况数与总情况数之比.
13.2
【分析】把代入方程计算即可求出的值.
【详解】解:把代入方程得:,
去括号得:,
解得:,
故答案为:2
【点睛】此题考查了一元二次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
14.3
【分析】过点C作 轴于点F,过点D作 轴于点E,作 于G,求出D点坐标,代入双曲线,求出双曲线的解析式,再求出C点坐标,根据平移的性质,得到平移后C点的新坐标,代入双曲线即可求出m的值
【详解】如图,过点C作 轴于点F,过点D作 轴于点E,作 于G,
直线y=﹣2x+4与x轴,y轴分别相交于点A、B,
当 时, ,即
当 时, ,即
四边形ABCD是正方形,
在 和 中,
,
D点坐标为(6,2),
把D点坐标代入双曲线 ,得
则双曲线的解析式为:
同理,
且
四边形DEFG是正方形
C点坐标为(4,6)
当正方形向下平移m个单位后,C点坐标变为(4,6-m),代入双曲线,
得 ,
解得 .
故答案为:3
【点睛】本题考查函数与几何图形的综合知识,难点在于作辅助线把两者连线起来.
15./
【分析】过点A作于点G,先证,得出,利用含30度角的直角三角形的性质、勾股定理可得,,代入求出,,再通过解求出,则.
【详解】解:过点A作于点G,如图,
∵,,
∴,
∵,
∴,
∴,
即,
∵,
∴,
∴,
∵,
∴,
∴,
∵点F是的中点,
∴,
∴ ,
∴,,
解得: , ,
在中,,
∴,
解得: ,
∴.
故答案为:.
【点睛】本题考查等腰三角形的性质,相似三角形的判定与性质,含30度角的直角三角形的性质,勾股定理,解直角三角形等,解题的关键是正确作出辅助线.
16.
【分析】根据化简绝对值,求一个数的立方根,特殊角的三角函数值,负指数幂,进行计算即可求解.
【详解】解:原式=
【点睛】本题考查了实数的混合运算,正确的计算是解题的关键.
17.,
【分析】先将小括号内的式子进行通分计算,然后再算括号外面的除法,最后代入求值.
【详解】解:原式
当时,原式
【点睛】本题考查分式的化简求值,二次根式的分母有理化计算,理解二次根式的性质,掌握分式混合运算的运算顺序(先算乘方,然后算乘除,最后算加减,有小括号先算小括号里面的)和计算法则是解题关键.
18.(1)24,图见解析
(2)36
(3)人
【分析】(1)根据D组人数和所占百分比即可求出被抽取学生总数,总数减去A、B、D组人数即可得到C组人数,补全统计图即可;
(2)用被抽取的学生成绩在A组的百分比乘即可;
(3)用全校人数乘以B组的百分比即可得到答案.
【详解】(1)解:被抽取学生总数为(人),
(人),
即被抽取的学生成绩在C组的有24人,
故答案为:24
补全条形统计图如下:
(2),
即被抽取的学生成绩在A组的对应扇形圆心角的度数是;
故答案为:36
(3)(人),即成绩在B组的大约有人.
【点睛】此题考查了扇形统计图和条形统计图,读懂题意,从图中获取信息是解题的关键.
19.(1)海绵飞盘和橡胶飞盘的进货单价分别是4元和10元
(2)第二批购进橡胶飞盘200个时,全部售完后,第二批飞盘获得利润最大,第二批飞盘的最大利润是1000元
【分析】(1)设海绵飞盘每个x元,则橡胶飞盘每个元,然后根据用620元购进30个海绵飞盘和50个橡胶飞盘列出方程求解即可;
(2)设第二批购进橡胶飞盘m个,利润为w元,则购进海绵飞盘个,然后根据利润单件利润数量列出w关于m的一次函数关系式,再根据橡胶飞盘数量不多于海绵飞盘数量的2倍求出m的取值范围,即可利用一次函数的性质求解.
【详解】(1)解:设海绵飞盘每个x元,则橡胶飞盘每个元,
由题意得,,
解得,
∴,
∴海绵飞盘和橡胶飞盘的进货单价分别是4元和10元;
(2)解:设第二批购进橡胶飞盘m个,利润为w元,则购进海绵飞盘个,
由题意得,,
∵橡胶飞盘数量不多于海绵飞盘数量的2倍,
∴,
∴,
∵,
∴w随m增大而增大,
∴当时,w最大,最大值为元,
∴第二批购进橡胶飞盘200个时,全部售完后,第二批飞盘获得利润最大,第二批飞盘的最大利润是1000元.
【点睛】本题主要考查了一元一次方程的实际运用,一次函数的实际应用,一元一次不等式的实际运用,正确理解题意列出对应的方程和函数关系式是解题的关键.
20.(1)13,59.9
(2)见解析
(3)增强;降低
(4)10分钟或16分钟
【分析】(1)根据二次函数的解析式将其改写成顶点式的形式即可;
(2)根据表格中的数据描点连线即可;
(3)根据图象解答即可;
(4)令, 求出x的值即可.
【详解】(1)
,
故答案为:13,59.9;
(2)如图;
(3)∵,
∴抛物线开口向下,对称轴是直线x=13,
当时,学生的接受能力逐步增强;
当时,学生的接受能力逐步降低.
故答案为:增强;降低;.
(4)当时,,
解得,,
某同学对概念的接受能力达到59时,提出概念所用的时间是10分钟或16分钟.
【点睛】本题考查了二次函数的应用,在解题时注意数形结合思想的运用是解题关键.
21.(1)四边形是矩形,理由见解析
(2)
(3)
【分析】(1)由三角形中位线定理可得,可证,即可求解;
(2)由勾股定理可求的长,由中点的性质可得的长,由锐角三角函数可求解;
(3)通过证明点,点,点,点四点共圆,可得,由直角三角形的性质可求的长,即可求解.
【详解】(1)解:四边形是矩形,理由如下:
点是的中点,点是的中点,
,
,
,
,
,
四边形是矩形;
(2)如图2,过点作于,
,,,
,
点是的中点,
,
,
,,
,
,
又,
,
,
,
;
(3)如图③,连接,,过点作于,
,,
,
,
点,点,点,点四点共圆,
,
,
,
,
,,
,
,
,
,
,
,,
.
【点睛】本题是三角形综合题,考查了矩形的判定,直角三角形的性质,勾股定理,锐角三角函数,圆的有关知识,灵活运用这些性质解决问题是解题的关键.
22.(1)证明见解析(2)(3)
【分析】(1)根据正方形的性质证明三角形全等即可;
(2)过点O作的平行线交于点E、交于点P,过点N作垂线交于点Q,构造相似三角形,对应边成比例求,然后根计算即可;
(3)过点O作的垂线交于点H,用勾股定理求出,证、,结合与重叠部分的面积是的面积的,设列出方程求出m,根据勾股定理求出即可.
【详解】(1)证明:∵四边形是正方形,
,,,
由旋转可知:,
,
,
,
;
(2)解:如图2,过点O作的平行线交于点E、交于点P,过点N作垂线交于点Q,
∵四边形和四边形都是矩形,,,,
,,
,,
,,
,
,
,
,
,
;
(3)解:如图,过点O作的垂线交于点H,
设,则,
设,则,
,,
,
,
,
,,四边形和四边形都是平行四边形,是直角三角形,
,
,
,,
,
,
,
,
,
,
,
,
设,则,
,
,
,
,
与重叠部分的面积是的面积的,平行四边形对角线平分平行四边形的面积,
,
,
,
,
.
【点睛】本题是四边形的综合题,考查了全等三角形的判定与性质、勾股定理、平行四边形、矩形、正方形的性质、相似三角形的判定与性质,熟练掌握相关性质与判定是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024年深圳市中考数学一轮模拟卷(二)
一、单选题
1.下列实数中,最大的数是( )
A. B. C. D.3
2.今年是中国共产党建党100周年,过去的100年是奋斗的100年,中国在各个方面都取得了巨大的成就.2020年GDP同比增长2.3%,GDP总量达到约102万亿元,其中102万用科学记数法表示为( )
A.10.2×105 B.1.02×106 C.1.02×105 D.10.2×104
3.在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )
A.6个 B.15个 C.13个 D.12个
4.不等式组的解集是( )
A.x>2 B.﹣3<x<2 C.﹣1<x<2 D.﹣2<x<2
5.关于数据3,,,0,5的说法正确的是( )
A.平均数为 B.中位数为1 C.众数为5 D.方差为6.8
6.关于一元二次方程根的情况,下列说法中正确的是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
7.如图,火车匀速通过隧道(隧道长等于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图像描述大致是( )
A. B.
C. D.
8.如图,在平行四边形ABCD中,AB=5,BC=8,以点D为圆心,任意长为半径画弧,交AD于点P,交CD于点Q,分别以P、Q为圆心,大于PQ为半径画弧交于点M,连接DM并延长,交BC于点E,连接AE,恰好有AE⊥BC,则AE的长为( )
A.3 B.4 C.5 D.
9.甲、乙两个工厂生产同一种类型口罩,每个小时甲厂比乙厂多生产1000个这种类型的口罩,甲厂生产30000个这种类型的口罩所用的时间与乙厂生产25000个这种类型的口罩的时间相同.设甲厂每小时生产这种类型的口罩x个,依据题意列方程为( )
A.= B.=
C.= D.=
10.如图,在矩形中,,E为中点,连接交于点F,连,下列结论:①;②;③;④.正确的有( )个.
A.1 B.2 C.3 D.4
二、填空题
11.因式分解: .
12.假期前,小明家设计了3种度假方案:参观动植物园、看电影、近郊露营.妈妈将三种方案分别写在3张相同的卡片上,小明随机抽取1张,他抽到去近郊露营的概率是 .
13.已知关于x的一元二次方程的一个根为1,则m= .
14.如图,直线y=﹣2x+4与x轴,y轴分别相交于点A、B,四边形ABCD是正方形,双曲线在第一象限经过点D,将正方形向下平移m个单位后,点C刚好落在双曲线上,则m= .
15.如图,已知在中,,,点D在边上,连接.以为斜边作,且,边的中点F恰好落在边上.若,则 .
三、解答题
16.计算:.
17.先化简,再求值:,其中.
18.济南某中学全校学生参加了“庆祝中国共青团成立100周年”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:分以下(不包括70);;;,并绘制出不完整的统计图.
(1)被抽取的学生成绩在C组的有______人,请补全条形统计图;
(2)被抽取的学生成绩在A组的对应扇形圆心角的度数是______度;
(3)若该中学全校共有2400人,则成绩在B组的大约有多少人?
19.飞盘运动由于门槛低、限制少,且具有较强的团体性和趣味性,在全国各地悄然兴起,深受年轻人喜爱,某商家拟用620元购进30个海绵飞盘和50个橡胶飞盘,已知橡胶飞盘的进货单价比海绵飞盘的进价单价多6元.
(1)海绵飞盘和橡胶飞盘的进货单价分别是多少元
(2)由于飞盘畅销,商家决定再购进这两种飞盘共300个,其中橡胶飞盘数量不多于海绵飞盘数量的2倍,且每种飞盘的进货单价保持不变,若橡胶飞盘的销售单价为14元,海绵的销售单价为6元,试问第二批购进橡胶飞盘多少个时,全部售完后,第二批飞盘获得利润最大?第二批飞盘的最大利润是多少元?
20.心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(单位:分)之间满足函数关系,y值越大,表示接受能力越强.
x
0 43
5 53.5
h k
20 55
30 31
(1)点是二次函数的顶点,则 , ;
(2)用光滑的曲线在所给的坐标系中画出二次函数的图象;
(3)根据图象,当内,学生的接受能力逐步 (填“增强”,“不变”或“降低”);,学生的接受能力逐步 (填“增强”,“不变”或“降低”).
(4)某同学对概念的接受能力达到59时,提出概念所用的时间是多少分钟?
21.综合与实践
问题情境:在中,,,.直角三角板中,将三角板的直角顶点放在斜边的中点处,并将三角板绕点旋转,三角板的两边,分别与边,交于点M,N.
猜想证明:
(1)如图①,在三角板旋转过程中,当点M为边的中点时,试判断四边形的形状,并说明理由;
问题解决:
(2)如图②,在三角板旋转过程中,当时,请直接写出的长;
(3)如图③,在三角板旋转过程中,当时,请求出线段的长.
22.(1)【探究发现】如图1,正方形的对角线相交于点O,在正方形绕点O旋转的过程中,边与边交于点M,边与边交于点N.证明: ;
(2)【类比迁移】如图2,矩形的对角线相交于点O,且,,在矩形,绕点O旋转的过程中,边与边交于点M,边与边交于点N.若,求的长;
(3)【拓展应用】如图3,四边形和四边形都是平行四边形,且,,,是直角三角形,在绕点O旋转的过程中,边与边交于点M,边与边交于点N.当与重叠部分的面积是的面积的时,请直接写出的长.
参考答案:
1.A
【分析】直接根据实数的大小比较法则比较数的大小即可.
【详解】解:,,,
∴,
故选:A.
【点睛】本题考查了实数的大小比较,关键要熟记:正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小.
2.B
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.
【详解】解:102万=1020000=1.02×106.
故选:B.
【点睛】此题主要考查了用科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|<10,确定a与n的值是解题的关键.
3.D
【详解】解:设白球个数为:x个,
∵摸到红色球的频率稳定在25%左右,∴口袋中得到红色球的概率为25%.
∴,解得:x=12.
经检验:x=12是原方程的解
∴白球的个数为12个.
故选D.
4.D
【分析】先求出两个不等式的解集,然后再写出不等式组的解集即可.
【详解】,
解①得:x>﹣2,
解②得:x<2,
故不等式组的解集是:﹣2<x<2,故D正确.
故选:D.
【点睛】本题主要考查了解一元一次不等式组,正确解出两个不等式的解集,是解题的关键.
5.D
【分析】根据平均数,中位数,众数和方差的求法逐一进行判断即可.
【详解】A,平均数为 ,故该选项错误;
B,中位数为0,故该选项错误;
C,所有数据都是出现了1次,所以这组数据没有众数;
D,方差为,故该选项正确;
故选:D.
【点睛】本题主要考查数据分析,掌握平均数,中位数,众数和方差的求法是解题的关键.
6.A
【分析】直接利用一元二次方程根的判别式即可得.
【详解】解:
其中,,,
∴,
∴方程有两个不相等的实数根.
故选:A.
【点睛】本题考查了一元二次方程根的判别式,熟练掌握一元二次方程根的判别式是解题关键.
7.B
【详解】解:根据题意可知火车进入隧道的时间x与火车在隧道内的长度y之间的关系具体可描述为:
当火车开始进入时y逐渐变大,当火车完全进入隧道,由于隧道长等于火车长,此时y最大,当火车开始出来时y逐渐变小.另外是匀速运动,y随x的均匀变化而均匀变化,故图象呈直线型,排除选项C.
故选:B.
8.B
【分析】由题意可知,再利用平行四边形的性质即可证明,即,即可求出,最后在中,利用勾股定理即可求出AE的长.
【详解】根据作图可知DE为的角平分线,即,
∵四边形ABCD为平行四边形,
∴,
∴,
∴,
∴,
∴,
∴在中,.
故选B.
【点睛】本题考查角平分线的判定和性质,平行四边形的性质,等腰三角形的判定和性质以及勾股定理.理解题意,判断出DE为的角平分线是解答本题的关键.
9.C
【分析】直接利用甲厂生产30000个和乙厂生产25000个口罩的时间相同得出等式即可.
【详解】解:设甲厂每小时生产这种类型的口罩个,依据题意列方程为:
.
故选:C.
【点睛】本题考查了根据实际问题列分式方程,找到等量关系是解题的关键.
10.C
【分析】利用矩形的性质,勾股定理及相似三角形的判定与性质即可解答.
【详解】解:①为中点,
,
,
,
,
,
,
,
,
,故①正确;
②过点作于点,如图,
设,则,,
,,
,
,
设,则,
在中,,
即,
解得:,
,
在中,由勾股定理得,
,
即,
,
,
,
故,故②错误;
③,,
,
,
,
,
,,
,故③正确;
④如图,
在,由勾股定理得,
,,
在,由勾股定理得,
,
在,由勾股定理得,
,故④正确;
故选:C.
【点睛】本题考查了矩形的性质,勾股定理的运用,相似三角形的性质等知识,关键能运用这些知识表示出需要的边或角,即可解决.
11..
【分析】直接运用完全平方公式进行分解即可.
【详解】解:.
故答案为:
【点睛】本题考查了因式分解,掌握完全平方公式是解题关键.
12.
【分析】直接根据概率公式求解即可.
【详解】解:∵妈妈将三种方案分别写在3张相同的卡片上,即共有3种等可能结果,
∴小明随机抽取1张,他抽到去近郊露营的概率是.
故答案为:.
【点睛】本题考查了概率,熟练掌握概率公式是解本题的关键.概率等于所求情况数与总情况数之比.
13.2
【分析】把代入方程计算即可求出的值.
【详解】解:把代入方程得:,
去括号得:,
解得:,
故答案为:2
【点睛】此题考查了一元二次方程的解,方程的解即为能使方程左右两边相等的未知数的值.
14.3
【分析】过点C作 轴于点F,过点D作 轴于点E,作 于G,求出D点坐标,代入双曲线,求出双曲线的解析式,再求出C点坐标,根据平移的性质,得到平移后C点的新坐标,代入双曲线即可求出m的值
【详解】如图,过点C作 轴于点F,过点D作 轴于点E,作 于G,
直线y=﹣2x+4与x轴,y轴分别相交于点A、B,
当 时, ,即
当 时, ,即
四边形ABCD是正方形,
在 和 中,
,
D点坐标为(6,2),
把D点坐标代入双曲线 ,得
则双曲线的解析式为:
同理,
且
四边形DEFG是正方形
C点坐标为(4,6)
当正方形向下平移m个单位后,C点坐标变为(4,6-m),代入双曲线,
得 ,
解得 .
故答案为:3
【点睛】本题考查函数与几何图形的综合知识,难点在于作辅助线把两者连线起来.
15./
【分析】过点A作于点G,先证,得出,利用含30度角的直角三角形的性质、勾股定理可得,,代入求出,,再通过解求出,则.
【详解】解:过点A作于点G,如图,
∵,,
∴,
∵,
∴,
∴,
即,
∵,
∴,
∴,
∵,
∴,
∴,
∵点F是的中点,
∴,
∴ ,
∴,,
解得: , ,
在中,,
∴,
解得: ,
∴.
故答案为:.
【点睛】本题考查等腰三角形的性质,相似三角形的判定与性质,含30度角的直角三角形的性质,勾股定理,解直角三角形等,解题的关键是正确作出辅助线.
16.
【分析】根据化简绝对值,求一个数的立方根,特殊角的三角函数值,负指数幂,进行计算即可求解.
【详解】解:原式=
【点睛】本题考查了实数的混合运算,正确的计算是解题的关键.
17.,
【分析】先将小括号内的式子进行通分计算,然后再算括号外面的除法,最后代入求值.
【详解】解:原式
当时,原式
【点睛】本题考查分式的化简求值,二次根式的分母有理化计算,理解二次根式的性质,掌握分式混合运算的运算顺序(先算乘方,然后算乘除,最后算加减,有小括号先算小括号里面的)和计算法则是解题关键.
18.(1)24,图见解析
(2)36
(3)人
【分析】(1)根据D组人数和所占百分比即可求出被抽取学生总数,总数减去A、B、D组人数即可得到C组人数,补全统计图即可;
(2)用被抽取的学生成绩在A组的百分比乘即可;
(3)用全校人数乘以B组的百分比即可得到答案.
【详解】(1)解:被抽取学生总数为(人),
(人),
即被抽取的学生成绩在C组的有24人,
故答案为:24
补全条形统计图如下:
(2),
即被抽取的学生成绩在A组的对应扇形圆心角的度数是;
故答案为:36
(3)(人),即成绩在B组的大约有人.
【点睛】此题考查了扇形统计图和条形统计图,读懂题意,从图中获取信息是解题的关键.
19.(1)海绵飞盘和橡胶飞盘的进货单价分别是4元和10元
(2)第二批购进橡胶飞盘200个时,全部售完后,第二批飞盘获得利润最大,第二批飞盘的最大利润是1000元
【分析】(1)设海绵飞盘每个x元,则橡胶飞盘每个元,然后根据用620元购进30个海绵飞盘和50个橡胶飞盘列出方程求解即可;
(2)设第二批购进橡胶飞盘m个,利润为w元,则购进海绵飞盘个,然后根据利润单件利润数量列出w关于m的一次函数关系式,再根据橡胶飞盘数量不多于海绵飞盘数量的2倍求出m的取值范围,即可利用一次函数的性质求解.
【详解】(1)解:设海绵飞盘每个x元,则橡胶飞盘每个元,
由题意得,,
解得,
∴,
∴海绵飞盘和橡胶飞盘的进货单价分别是4元和10元;
(2)解:设第二批购进橡胶飞盘m个,利润为w元,则购进海绵飞盘个,
由题意得,,
∵橡胶飞盘数量不多于海绵飞盘数量的2倍,
∴,
∴,
∵,
∴w随m增大而增大,
∴当时,w最大,最大值为元,
∴第二批购进橡胶飞盘200个时,全部售完后,第二批飞盘获得利润最大,第二批飞盘的最大利润是1000元.
【点睛】本题主要考查了一元一次方程的实际运用,一次函数的实际应用,一元一次不等式的实际运用,正确理解题意列出对应的方程和函数关系式是解题的关键.
20.(1)13,59.9
(2)见解析
(3)增强;降低
(4)10分钟或16分钟
【分析】(1)根据二次函数的解析式将其改写成顶点式的形式即可;
(2)根据表格中的数据描点连线即可;
(3)根据图象解答即可;
(4)令, 求出x的值即可.
【详解】(1)
,
故答案为:13,59.9;
(2)如图;
(3)∵,
∴抛物线开口向下,对称轴是直线x=13,
当时,学生的接受能力逐步增强;
当时,学生的接受能力逐步降低.
故答案为:增强;降低;.
(4)当时,,
解得,,
某同学对概念的接受能力达到59时,提出概念所用的时间是10分钟或16分钟.
【点睛】本题考查了二次函数的应用,在解题时注意数形结合思想的运用是解题关键.
21.(1)四边形是矩形,理由见解析
(2)
(3)
【分析】(1)由三角形中位线定理可得,可证,即可求解;
(2)由勾股定理可求的长,由中点的性质可得的长,由锐角三角函数可求解;
(3)通过证明点,点,点,点四点共圆,可得,由直角三角形的性质可求的长,即可求解.
【详解】(1)解:四边形是矩形,理由如下:
点是的中点,点是的中点,
,
,
,
,
,
四边形是矩形;
(2)如图2,过点作于,
,,,
,
点是的中点,
,
,
,,
,
,
又,
,
,
,
;
(3)如图③,连接,,过点作于,
,,
,
,
点,点,点,点四点共圆,
,
,
,
,
,,
,
,
,
,
,
,,
.
【点睛】本题是三角形综合题,考查了矩形的判定,直角三角形的性质,勾股定理,锐角三角函数,圆的有关知识,灵活运用这些性质解决问题是解题的关键.
22.(1)证明见解析(2)(3)
【分析】(1)根据正方形的性质证明三角形全等即可;
(2)过点O作的平行线交于点E、交于点P,过点N作垂线交于点Q,构造相似三角形,对应边成比例求,然后根计算即可;
(3)过点O作的垂线交于点H,用勾股定理求出,证、,结合与重叠部分的面积是的面积的,设列出方程求出m,根据勾股定理求出即可.
【详解】(1)证明:∵四边形是正方形,
,,,
由旋转可知:,
,
,
,
;
(2)解:如图2,过点O作的平行线交于点E、交于点P,过点N作垂线交于点Q,
∵四边形和四边形都是矩形,,,,
,,
,,
,,
,
,
,
,
,
;
(3)解:如图,过点O作的垂线交于点H,
设,则,
设,则,
,,
,
,
,
,,四边形和四边形都是平行四边形,是直角三角形,
,
,
,,
,
,
,
,
,
,
,
,
设,则,
,
,
,
,
与重叠部分的面积是的面积的,平行四边形对角线平分平行四边形的面积,
,
,
,
,
.
【点睛】本题是四边形的综合题,考查了全等三角形的判定与性质、勾股定理、平行四边形、矩形、正方形的性质、相似三角形的判定与性质,熟练掌握相关性质与判定是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
