苏科版 数学七年级上册 4.1 从问题到方程 课件 (共22张PPT)
文档属性
| 名称 | 苏科版 数学七年级上册 4.1 从问题到方程 课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 14:52:42 | ||
图片预览








文档简介
4.1从问题到方程
苏科版七年级上册 数学
在现实世界的许多实际问题中,通常有已知的量和未知的量,这些数量之间常常有相等的关系.
左盘内物体的质量=右盘内砝码的质量
当天平平衡的时候
问题1:如图,在天平左盘中有两个质量相等的小球和一个1g的砝码,天平的右盘内有一个5g的砝码,怎样描述天平平衡所表示的数量关系?
两个相同的小球质量+1g的砝码
=右盘中砝码的质量
2x+1=5
设两个相同小球的质量都是xg,
方程是表达数量之间相等关系的“天平”,是解决实际问题的有效模型。
感受方程魅力
两个相同的小球质量+1g的砝码
=右盘中砝码的质量
2x+1=5
设两个相同小球的质量都是xg,
实际问题
数学问题
(方程问题)
抽象
感受方程魅力
问题2:某校举行篮球联赛,规则规定:胜一场得2分,负一场得1分.该队赛了12场,共得20分,怎样描述其中数量之间的相等关系?
建立方程模型
胜的场数+负的场数=12场
胜的分数+负的分数=20分
实际问题中数量之间的相等关系,可以用多种不同的方式描述。通过比较可以看出,用方程描述相等关系最简明。
解:设胜x场,则负(12-x)场,
得到方程: 2x+(12-x)=20
找相等关系:
变式:若得分规则改为:胜一场得2分,平一场得1分,负一场得0分。该队赛了14场,负了5场,共得13分,怎样描述其中数量之间的相等关系?
胜的场数+平的场数+负的场数=14场
胜的分数+平的分数+负的分数=13分
找相等关系:
解:设胜x场,
则平(14-5-x)场,
得到方程:
2x+(14-5-x)=13
建立方程模型
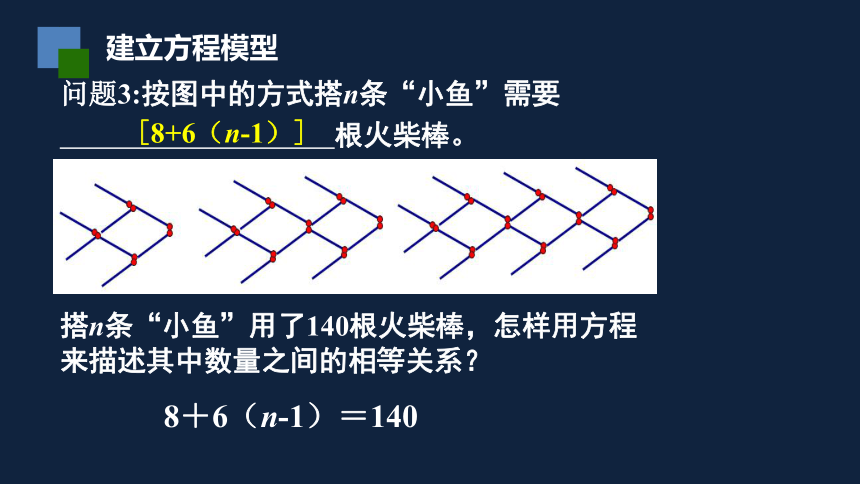
问题3:按图中的方式搭n条“小鱼”需要
根火柴棒。
搭n条“小鱼”用了140根火柴棒,怎样用方程来描述其中数量之间的相等关系?
8+6(n-1)=140
[8+6(n-1)]
建立方程模型
解:(1) x年后小红的年龄是(5+x),爸爸的年龄是(32+x)。
问题4:今年小红5岁,爸爸32岁。
(1)用代数式分别表示x年后小红与爸爸的年龄;
(2)如果x年后小红的年龄是爸爸年龄的???????? ,怎样用方程来描述其中数量之间的相等关系?
?
x年后小红的年龄=x年后爸爸年龄×????????
?
(2)找相等关系:
得到方程:5+x=????????(32+x)
?
建立方程模型
形成方法
思考:从实际问题到方程要经历哪些过程?
(2)找出相等关系;
(3)设未知量x;
(4)根据相等关系列方程.
(1)审题;
一元一次方程的定义:
只含有一个未知数(元),并且未知数的次数都是1(次),
像这样的方程叫做一元一次方程.
①
②
③整式方程
观察列出的方程:2x+1=5,2x+(12-x)=20,
2x+(14-5-x)=20,
方程概念
一个未知数(元)
次数都是1(次)
5+x=????????(32+x)
?
8+6(n-1)=140,
它们有什么共同特征呢?
练习:下列各式哪些是一元一次方程?
① ②
④
⑤ x+3>5 ⑥4﹣9=﹣5
不是
不是
不是
是
不是
不是
方程的数学文化
方程的数学文化
方程这个名词,最早见于我国古代算书《九章算术》,距离现在有2000多年的历史。
笛卡尔第一个提倡用x、y、z等字母表示未知数,才形成了现在的方程。
2x+15=210
方程的数学文化
例:我国古代问题:以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺。绳长、井深各几何?
方程应用
意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺。绳长、井深各几尺?
得到方程:????????x-4=????????x-1
?
井深:????????x-4
?
4尺
1尺
方法一:
井深:????????x-1
?
解:设绳长为x尺,
方程应用
意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺.绳长、井深各几尺?
解:设井深为x尺,
得到方程: 3(x+4)=4(x+1)
绳长:3(x+4)
4尺
1尺
绳长:4(x+1)
方法二:
来描述这个问题中的数量之间的相等关系.
方程应用
1.本节课你学习了哪些知识?学科网
2.我们是如何研究方程的?
小结提升
实际问题
数学问题
(方程)
抽象
一元一次方程
...方程
方程的解
解方程
知识框架
一切问题都可以转化为数学问题,
一切数学问题都可以转化为代数问题,
而一切代数问题都可以转化为方程问题。
因此,一旦解决了方程问题,所有问题将迎刃而解。
谢 谢 观 看!
苏科版七年级上册 数学
在现实世界的许多实际问题中,通常有已知的量和未知的量,这些数量之间常常有相等的关系.
左盘内物体的质量=右盘内砝码的质量
当天平平衡的时候
问题1:如图,在天平左盘中有两个质量相等的小球和一个1g的砝码,天平的右盘内有一个5g的砝码,怎样描述天平平衡所表示的数量关系?
两个相同的小球质量+1g的砝码
=右盘中砝码的质量
2x+1=5
设两个相同小球的质量都是xg,
方程是表达数量之间相等关系的“天平”,是解决实际问题的有效模型。
感受方程魅力
两个相同的小球质量+1g的砝码
=右盘中砝码的质量
2x+1=5
设两个相同小球的质量都是xg,
实际问题
数学问题
(方程问题)
抽象
感受方程魅力
问题2:某校举行篮球联赛,规则规定:胜一场得2分,负一场得1分.该队赛了12场,共得20分,怎样描述其中数量之间的相等关系?
建立方程模型
胜的场数+负的场数=12场
胜的分数+负的分数=20分
实际问题中数量之间的相等关系,可以用多种不同的方式描述。通过比较可以看出,用方程描述相等关系最简明。
解:设胜x场,则负(12-x)场,
得到方程: 2x+(12-x)=20
找相等关系:
变式:若得分规则改为:胜一场得2分,平一场得1分,负一场得0分。该队赛了14场,负了5场,共得13分,怎样描述其中数量之间的相等关系?
胜的场数+平的场数+负的场数=14场
胜的分数+平的分数+负的分数=13分
找相等关系:
解:设胜x场,
则平(14-5-x)场,
得到方程:
2x+(14-5-x)=13
建立方程模型
问题3:按图中的方式搭n条“小鱼”需要
根火柴棒。
搭n条“小鱼”用了140根火柴棒,怎样用方程来描述其中数量之间的相等关系?
8+6(n-1)=140
[8+6(n-1)]
建立方程模型
解:(1) x年后小红的年龄是(5+x),爸爸的年龄是(32+x)。
问题4:今年小红5岁,爸爸32岁。
(1)用代数式分别表示x年后小红与爸爸的年龄;
(2)如果x年后小红的年龄是爸爸年龄的???????? ,怎样用方程来描述其中数量之间的相等关系?
?
x年后小红的年龄=x年后爸爸年龄×????????
?
(2)找相等关系:
得到方程:5+x=????????(32+x)
?
建立方程模型
形成方法
思考:从实际问题到方程要经历哪些过程?
(2)找出相等关系;
(3)设未知量x;
(4)根据相等关系列方程.
(1)审题;
一元一次方程的定义:
只含有一个未知数(元),并且未知数的次数都是1(次),
像这样的方程叫做一元一次方程.
①
②
③整式方程
观察列出的方程:2x+1=5,2x+(12-x)=20,
2x+(14-5-x)=20,
方程概念
一个未知数(元)
次数都是1(次)
5+x=????????(32+x)
?
8+6(n-1)=140,
它们有什么共同特征呢?
练习:下列各式哪些是一元一次方程?
① ②
④
⑤ x+3>5 ⑥4﹣9=﹣5
不是
不是
不是
是
不是
不是
方程的数学文化
方程的数学文化
方程这个名词,最早见于我国古代算书《九章算术》,距离现在有2000多年的历史。
笛卡尔第一个提倡用x、y、z等字母表示未知数,才形成了现在的方程。
2x+15=210
方程的数学文化
例:我国古代问题:以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺。绳长、井深各几何?
方程应用
意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺。绳长、井深各几尺?
得到方程:????????x-4=????????x-1
?
井深:????????x-4
?
4尺
1尺
方法一:
井深:????????x-1
?
解:设绳长为x尺,
方程应用
意思是:用绳子量井深,把绳三折来量,井外余绳四尺;把绳四折来量,井外余绳一尺.绳长、井深各几尺?
解:设井深为x尺,
得到方程: 3(x+4)=4(x+1)
绳长:3(x+4)
4尺
1尺
绳长:4(x+1)
方法二:
来描述这个问题中的数量之间的相等关系.
方程应用
1.本节课你学习了哪些知识?学科网
2.我们是如何研究方程的?
小结提升
实际问题
数学问题
(方程)
抽象
一元一次方程
...方程
方程的解
解方程
知识框架
一切问题都可以转化为数学问题,
一切数学问题都可以转化为代数问题,
而一切代数问题都可以转化为方程问题。
因此,一旦解决了方程问题,所有问题将迎刃而解。
谢 谢 观 看!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
