4.5 全等三角形专题复习 课件 21张PPT 北师大版七年级数学下册
文档属性
| 名称 | 4.5 全等三角形专题复习 课件 21张PPT 北师大版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 685.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 15:22:11 | ||
图片预览

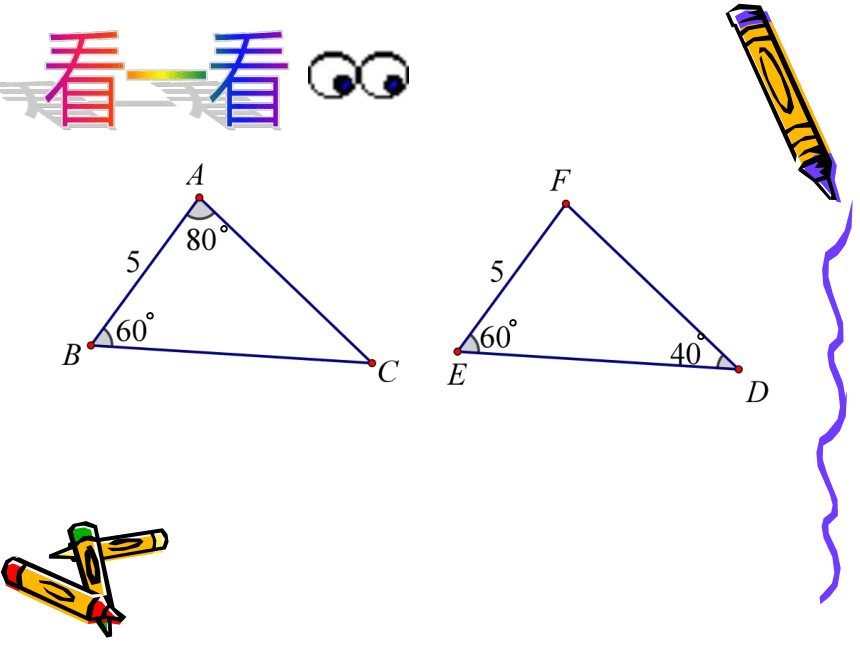
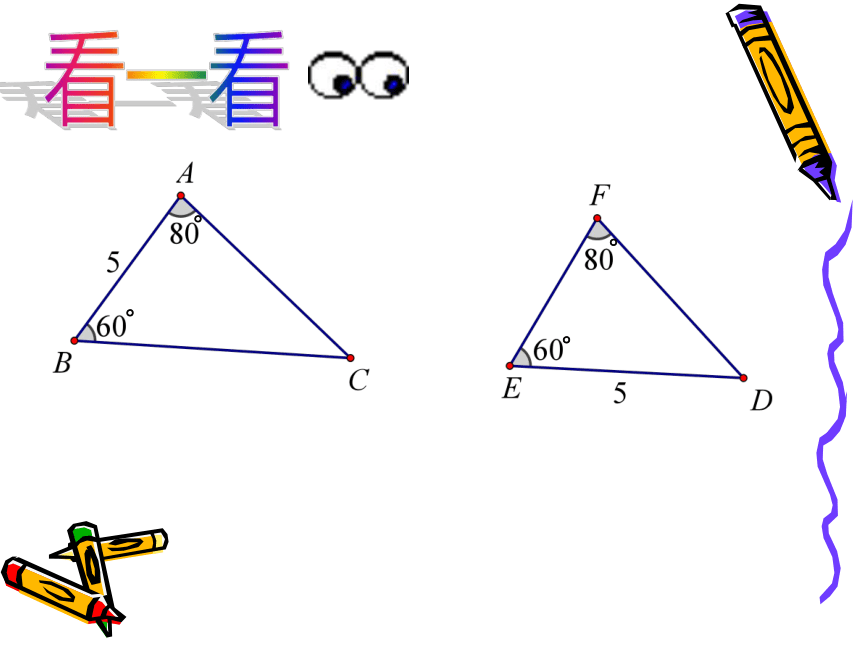
文档简介
(共21张PPT)
4.5三角形全等专题复习
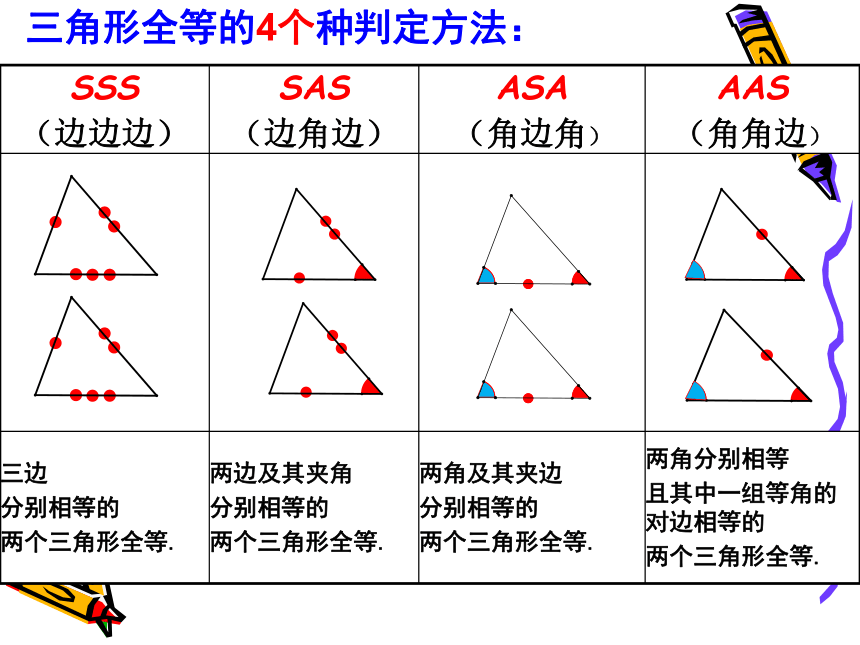
三角形全等的4个种判定方法:
SSS (边边边) SAS (边角边) ASA (角边角) AAS
(角角边)
三边 分别相等的 两个三角形全等. 两边及其夹角 分别相等的 两个三角形全等. 两角及其夹边 分别相等的 两个三角形全等. 两角分别相等
且其中一组等角的对边相等的
两个三角形全等.
看一看
°
°
°
°
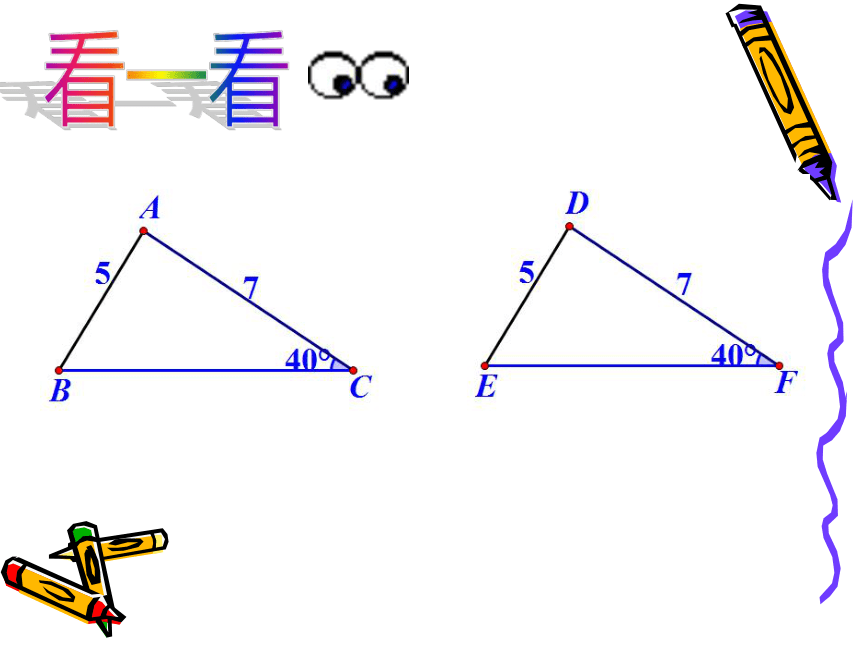
看一看
看一看
°
°
°
°
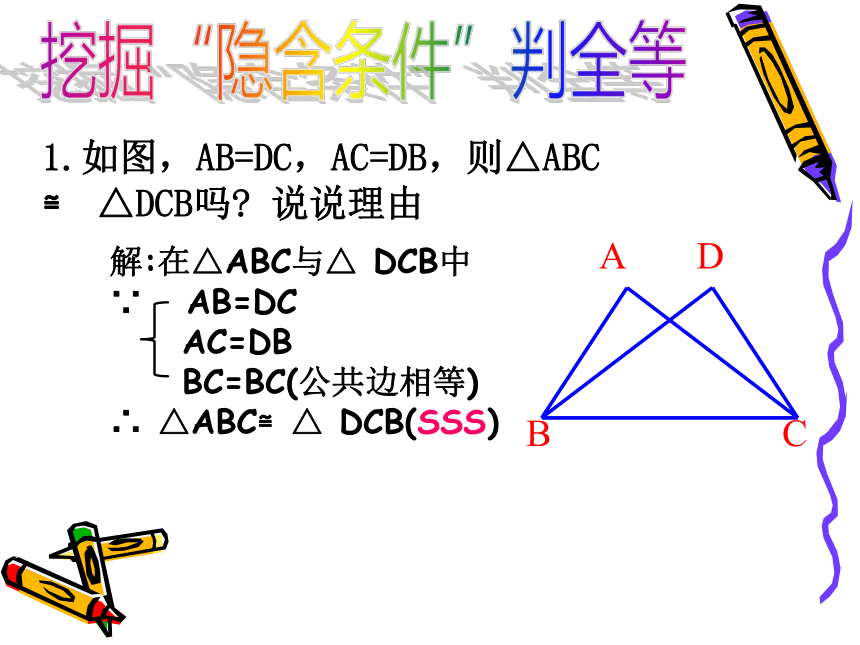
1.如图,AB=DC,AC=DB,则△ABC ≌ △DCB吗 说说理由
A
D
B
C
挖掘“隐含条件”判全等
解:在△ABC与△ DCB中
∵ AB=DC
AC=DB
BC=BC(公共边相等)
∴ △ABC≌△ DCB(SSS)
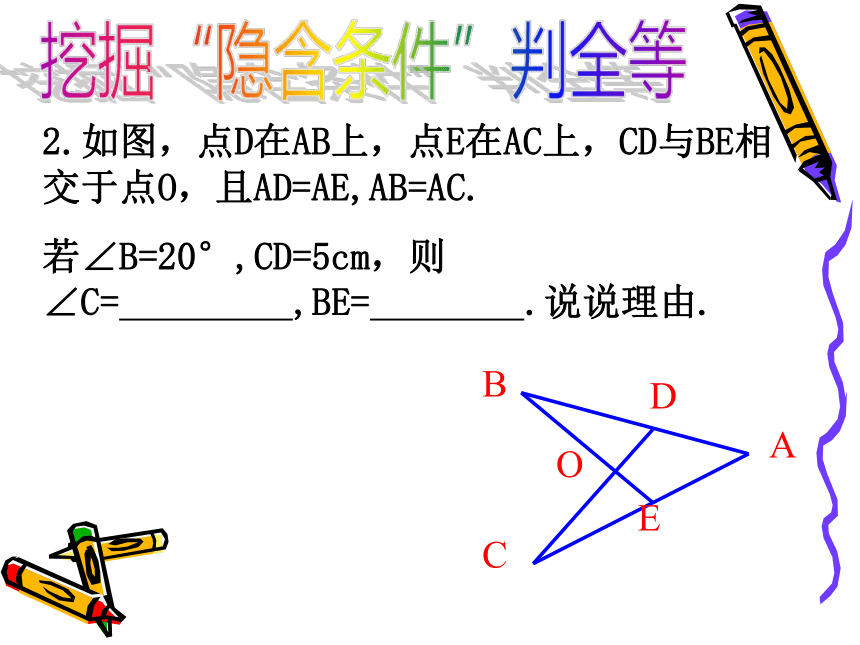
2.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.
若∠B=20°,CD=5cm,则∠C= ,BE= .说说理由.
B
C
O
D
E
A
挖掘“隐含条件”判全等
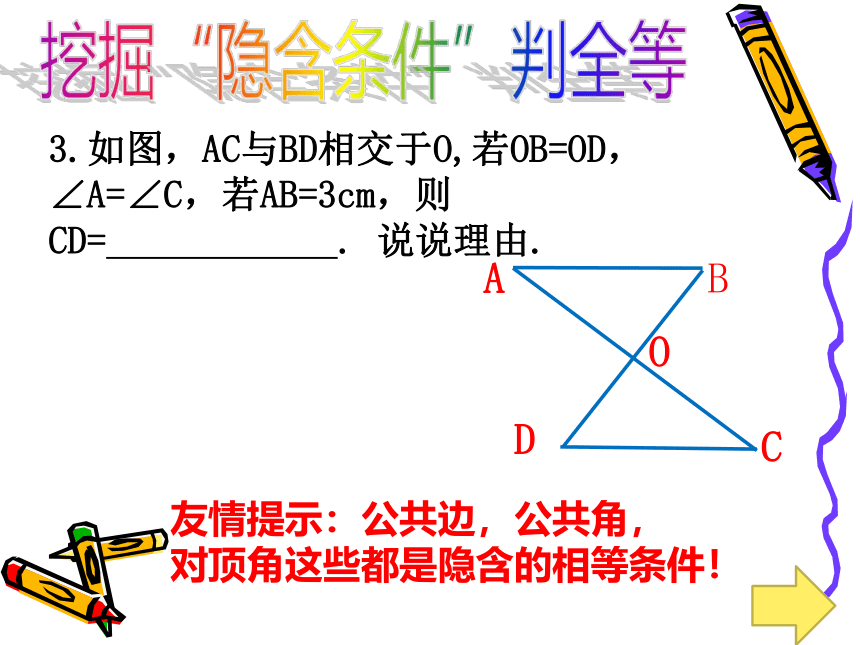
3.如图,AC与BD相交于O,若OB=OD,∠A=∠C,若AB=3cm,则CD= . 说说理由.
友情提示:公共边,公共角,
对顶角这些都是隐含的相等条件!
挖掘“隐含条件”判全等
A
B
D
C
O
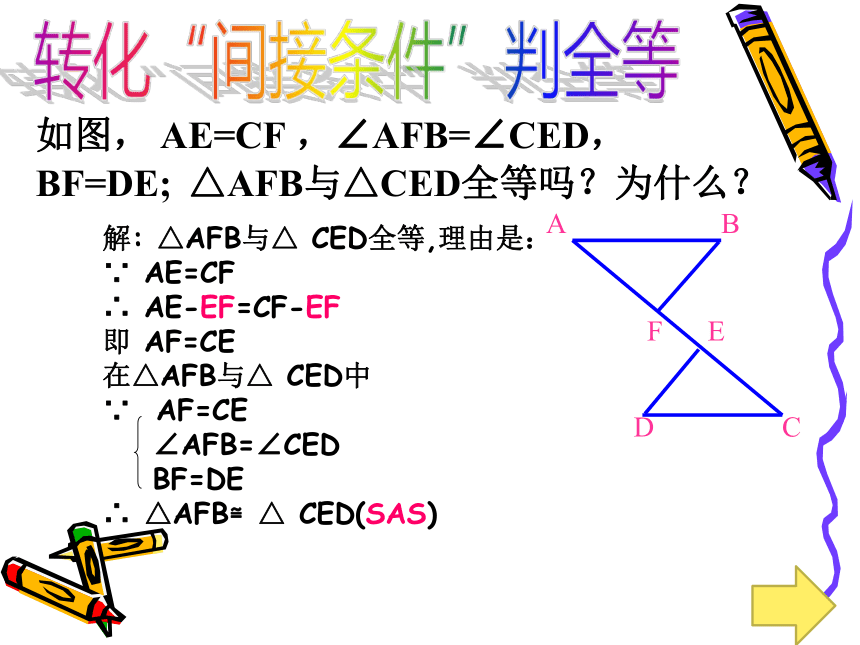
如图, AE=CF ,∠AFB=∠CED,BF=DE; △AFB与△CED全等吗?为什么?
A
B
D
C
F
E
转化“间接条件”判全等
解: △AFB与△ CED全等,理由是:
∵ AE=CF
∴ AE-EF=CF-EF
即 AF=CE
在△AFB与△ CED中
∵ AF=CE
∠AFB=∠CED
BF=DE
∴ △AFB≌△ CED(SAS)
如图,AE=AC,AD=AB ,∠1=∠2
求证:△ABC ≌ △ADE
辨认“基本图形”判全等
辨认“基本图形”判全等
如图,AE=AC,AD=AB ,∠1=∠2
你还能得到哪些结论?
数学应用于生活
小明一不小心把一块三角形的玻璃打碎成了两块,如图所示,现在他要去玻璃店配一块完全一样的玻璃,那么最省事的方法是带( )
①
②
数学应用于生活
小明一不小心把一块三角形的玻璃打碎成了三块,如图所示,现在他要去玻璃店配一块完全一样的玻璃,那么最省事的方法是( )
带①去
带②去
C. 带③去
D. 带①和②去
数学应用于生活
小明一不小心把一块三角形的玻璃打碎成了四块,如图所示,现在他要去玻璃店配一块完全一样的玻璃,那么最省事的方法是带几块去?带哪几块?
数学来源于生活
如图,小明家有一个玻璃容器,内部D点处有一只小飞虫,它要飞到内部B处觅食,它飞行的最短路径是什么?如何测量?容器边上有两根吸管,聪明的你能帮小明想个办法吗?
你有哪些收获呢?
与大家共分享!
学而不思则罔
回头一看,我想说…
1、已知:如图∠B=∠DEF, AB=DE,补充一个条件
使得ΔABC≌ ΔDEF
∠ACB= ∠F
BC=EF
D
E
F
A
B
C
∠ A = ∠ D
(1) 若要以“SAS”为依据,补充条件 _____;
(2) 若要以“ASA”为依据,补充条件____
(3) 若要以“AAS”为依据,补充条件_____.
达标检测
AC ∥ DF
BE=CF
达标检测
2、用直尺和圆规作一个角等于已知角的示意图如下,要说明∠A′O′B′=∠AOB,则需要证明△C′O′D′≌△COD,则这两个三角形全等的依据是 (写出全等的简写)
SSS
3、已知△AFD和△CEB中,点A,E,F,C
在同一条直线上,有如下四个论断:
(1)AD=CB (2)AE=CF (3)∠B=∠D(4)AD //BC 请用其中三个作为条件,一个作为结论,编一道数学问题并证明。
A
B
C
E
F
D
达标检测
作业布置
必做:P111 复习题6、9、11
选做:如图等边△ABC和等边△DCE,连接BD、AE交于点P。
(1)问BD=AE吗?说明理由。
(2)求∠APB
4.5三角形全等专题复习
三角形全等的4个种判定方法:
SSS (边边边) SAS (边角边) ASA (角边角) AAS
(角角边)
三边 分别相等的 两个三角形全等. 两边及其夹角 分别相等的 两个三角形全等. 两角及其夹边 分别相等的 两个三角形全等. 两角分别相等
且其中一组等角的对边相等的
两个三角形全等.
看一看
°
°
°
°
看一看
看一看
°
°
°
°
1.如图,AB=DC,AC=DB,则△ABC ≌ △DCB吗 说说理由
A
D
B
C
挖掘“隐含条件”判全等
解:在△ABC与△ DCB中
∵ AB=DC
AC=DB
BC=BC(公共边相等)
∴ △ABC≌△ DCB(SSS)
2.如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.
若∠B=20°,CD=5cm,则∠C= ,BE= .说说理由.
B
C
O
D
E
A
挖掘“隐含条件”判全等
3.如图,AC与BD相交于O,若OB=OD,∠A=∠C,若AB=3cm,则CD= . 说说理由.
友情提示:公共边,公共角,
对顶角这些都是隐含的相等条件!
挖掘“隐含条件”判全等
A
B
D
C
O
如图, AE=CF ,∠AFB=∠CED,BF=DE; △AFB与△CED全等吗?为什么?
A
B
D
C
F
E
转化“间接条件”判全等
解: △AFB与△ CED全等,理由是:
∵ AE=CF
∴ AE-EF=CF-EF
即 AF=CE
在△AFB与△ CED中
∵ AF=CE
∠AFB=∠CED
BF=DE
∴ △AFB≌△ CED(SAS)
如图,AE=AC,AD=AB ,∠1=∠2
求证:△ABC ≌ △ADE
辨认“基本图形”判全等
辨认“基本图形”判全等
如图,AE=AC,AD=AB ,∠1=∠2
你还能得到哪些结论?
数学应用于生活
小明一不小心把一块三角形的玻璃打碎成了两块,如图所示,现在他要去玻璃店配一块完全一样的玻璃,那么最省事的方法是带( )
①
②
数学应用于生活
小明一不小心把一块三角形的玻璃打碎成了三块,如图所示,现在他要去玻璃店配一块完全一样的玻璃,那么最省事的方法是( )
带①去
带②去
C. 带③去
D. 带①和②去
数学应用于生活
小明一不小心把一块三角形的玻璃打碎成了四块,如图所示,现在他要去玻璃店配一块完全一样的玻璃,那么最省事的方法是带几块去?带哪几块?
数学来源于生活
如图,小明家有一个玻璃容器,内部D点处有一只小飞虫,它要飞到内部B处觅食,它飞行的最短路径是什么?如何测量?容器边上有两根吸管,聪明的你能帮小明想个办法吗?
你有哪些收获呢?
与大家共分享!
学而不思则罔
回头一看,我想说…
1、已知:如图∠B=∠DEF, AB=DE,补充一个条件
使得ΔABC≌ ΔDEF
∠ACB= ∠F
BC=EF
D
E
F
A
B
C
∠ A = ∠ D
(1) 若要以“SAS”为依据,补充条件 _____;
(2) 若要以“ASA”为依据,补充条件____
(3) 若要以“AAS”为依据,补充条件_____.
达标检测
AC ∥ DF
BE=CF
达标检测
2、用直尺和圆规作一个角等于已知角的示意图如下,要说明∠A′O′B′=∠AOB,则需要证明△C′O′D′≌△COD,则这两个三角形全等的依据是 (写出全等的简写)
SSS
3、已知△AFD和△CEB中,点A,E,F,C
在同一条直线上,有如下四个论断:
(1)AD=CB (2)AE=CF (3)∠B=∠D(4)AD //BC 请用其中三个作为条件,一个作为结论,编一道数学问题并证明。
A
B
C
E
F
D
达标检测
作业布置
必做:P111 复习题6、9、11
选做:如图等边△ABC和等边△DCE,连接BD、AE交于点P。
(1)问BD=AE吗?说明理由。
(2)求∠APB
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
