江西省抚州市第一名校2023-2024学年高二上学期第二次综合素质测评(12月)数学试题(扫描版无答案)
文档属性
| 名称 | 江西省抚州市第一名校2023-2024学年高二上学期第二次综合素质测评(12月)数学试题(扫描版无答案) |  | |
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 08:42:24 | ||
图片预览


文档简介
抚州 中 2023-2024学年度上学期 年级第 次综合素质测评
数 学 试 卷
考试时 :120分钟, 分值:150分
注意事项:
1. 答题前,考 务必 碳素笔将 的姓名、准考证号、考场号、座位号在答题卡
上填写清楚.
2.每 题选出答案后, 2B铅笔把答题卡上对应题 的答案标号涂 ,如需改动, 橡
擦 净后,再选涂其他答案标号. 在试题卷上作答 效.
第Ⅰ卷(共 60 分)
、选择题:本 题共 8 题,每 题 5分,共 40分.在每 题给出的四个选项中只有
项是符合要求的.
1.抛物线 的焦点坐标是( )
A. (1,0) B. (0,1)
2.设 a∈R, 若直线 :ax+2y-8=0与直线 平 ,则 a的值为( )
A. 1 B. -2 C 1或-2
3.在某城市中,A,B两地有如图所示的 格型道路 ,甲随机沿道路 选择 条最短
路径,从 A地出发去往 B地,途经 C地,则不同的路线有( )
A. 90 种 B. 105 种 C. 260种 D. 315 种
4. 在直三棱柱 中, D,E分别为 AC,BC
的中点,则异 直线 C D与 B E所成 的余弦值为( )
学 科 ( 北 京 ) 股 份 有 限 公 司
5.已知椭圆 E 的右焦点为 F(3,0),过点 F的直线交椭圆 E于 A,
B两点,若 AB的中点坐标为(1,-1), 则椭圆 E的 程为( )
6. 已知圆 C: 与直线 l: mx-y+m+1=0(m≠0),过 l上任意 点 M向圆
C引切线,切点为 A,B, 若 的最 值为 则实数 m的值为( )
7. 如图,已知正 体. 棱 为 1,点 H 在棱 上,且
在侧 内作边 为 的正 形 P是侧 内 动点, 且点 P
到平 距离等于线段 PF的 , 则当点 P运动时, HP 的最 值是( )
8. 数学美的表现形式不同于 然美或艺术美那样直观,它蕴藏于特有的抽象概念,公式
符号,推理论证,思维 法等之中,揭示了规律性,是 种科学的真实美. 平 直 坐标系
中, 曲线 C: 就是 条形状优美的曲线,对于此曲线,给出如下结论:
①曲线 C围成的图形的 积是
②曲线 C围成的图形有 2条对称轴
③ 曲线 C上的任意两点间的距离不超过 2;
④ 若 P(m,n)是曲线 C上任意 点,则 的最 值是
其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
、选择题: 本 题共 4 题, 每 题 5分,共 20分.在每 题给出的选项中, 有多
项符合题 要求,全部选对的得 5分,部分选对的得 2分,有选错的得 0分.
9.给出下列命题, 其中正确的命题是( )
A. 过点(3,4)且在 x,y轴上的截距相等的直线 程为 x-y-7=0
B. 若直线 l的 向向量为 =(1,0,3), 平 α的法向量为 则直线 l//α
C. 点 P(L,1)在圆 内
D. 点 P(x,y)满 则点 P的轨迹是 个椭圆
10. 已 知 圆 与 圆
则( )
学 科 ( 北 京 ) 股 份 有 限 公 司
A. 若圆 C 与 x轴相切, 则 m=±2
B. 若 m=1, 则圆 C 与圆 C 相交
C. 当 时,两圆的公共弦 为
D. 直线 kx-y+3k+2=0与圆 C 始终有两个交点
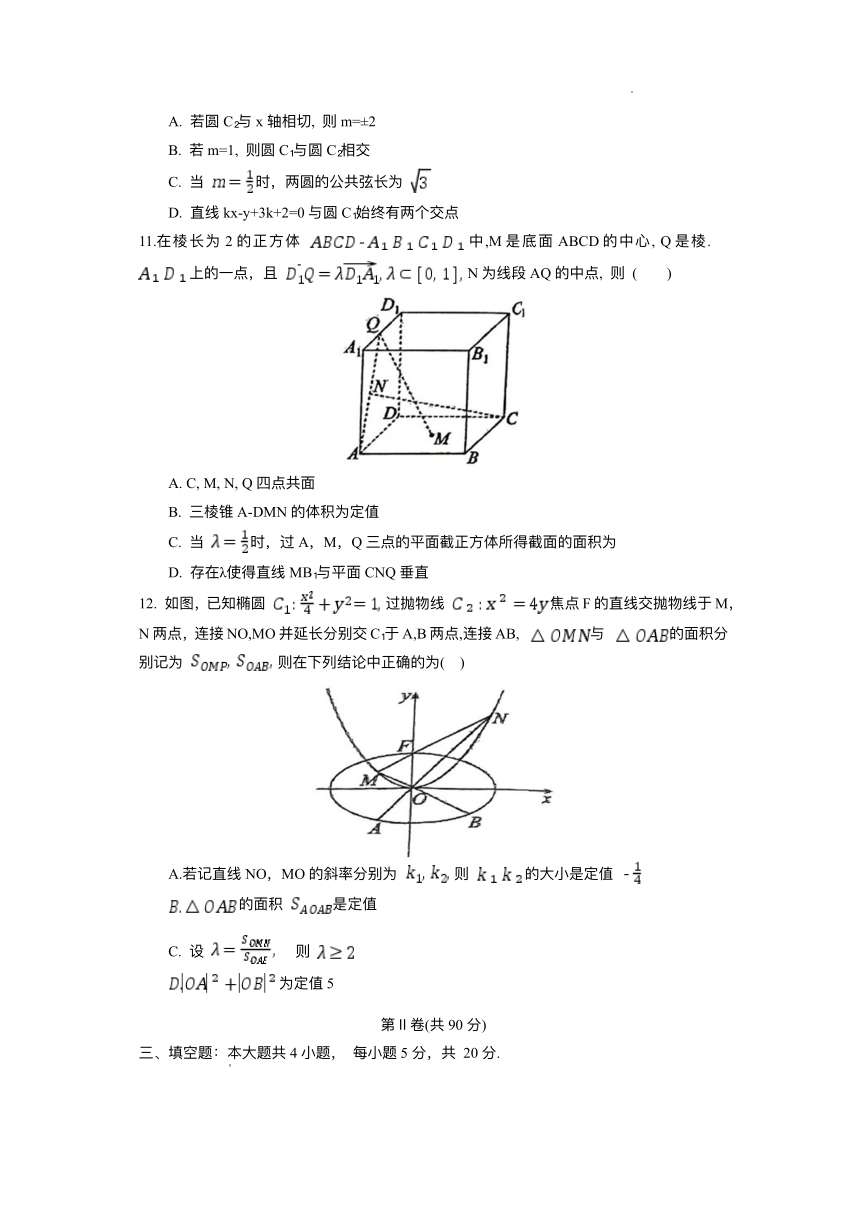
11.在棱 为 2的正 体 中 ,M是底 ABCD的中 , Q是棱 .
上的 点,且 N为线段 AQ的中点, 则 ( )
A. C, M, N, Q四点共
B. 三棱锥 A-DMN的体积为定值
C. 当 时,过 A,M,Q三点的平 截正 体所得截 的 积为
D. 存在λ使得直线MB 与平 CNQ垂直
12. 如图,已知椭圆 过抛物线 焦点 F的直线交抛物线于M,
N两点,连接NO,MO并延 分别交 C 于A,B两点,连接AB, 与 的 积分
别记为 则在下列结论中正确的为( )
A.若记直线 NO,MO的斜率分别为 则 的 是定值
的 积 是定值
C. 设 则
为定值 5
第Ⅱ卷(共 90分)
三、填空题:本 题共 4 题, 每 题 5分,共 20分.
学 科 ( 北 京 ) 股 份 有 限 公 司
13. 已知空间向量 则向量 在向量 上的投影向量的坐标
是 .
14. 已知 abc表示 个三位数, 如果满 且 那么我们称该三位数为“凸数”,
则没有重复数字的三位“凸数”的个数为 .
15. 如图, 过双曲线 的左焦点 引圆
的切线, 切点为 T, 延 FT交双曲线右 于 P点,M为线段 FP的中
点, O为坐标原点, 若 则双曲线的离 率为 .
16. 空间直 坐标系 xOy中, 过点. 且 个法向量为 的
平 α的 程为 过点 且
向向量为 的直线 l的 程为 阅读上 材料,
并解决下 问题:已知平 α的 程为. 直线 l是两个平 与
的交线,则直线 l与平 α所成 的正弦值为______________
四、解答题:本 题共 6 题,共 70分.解答题应写出必要的 字说明、证明过程或演算步
骤.
17.(本 题满分 10分)
(1)求值:
(2) 解不等式:
学 科 ( 北 京 ) 股 份 有 限 公 司
18.(本 题满分 12分)已知点 A(-1,2)和直线 l:6x-4y+1=0,点 B是点 A关于直线 l的对称点.
(1)求点 B的坐标;
(2)O为坐标原点, 且点 P满 若点 P的轨迹与直线
有公共点,求 m的取值范围.
19.(本 题满分 12分)
三棱柱 中, 线段
的中点为M ,且 BC⊥AM.
(1) 求证:
(2) 点 P在线段 上, 且 求平 与平 夹
的余弦值.
20.(本 题满分 12分)第 18届亚 联亚洲杯将于 2023年举 ,已知此次亚洲杯甲舰判组有
6名裁判,分别是 A、B。C、D、E、F、(以下问题 数字作答)
(1)若亚洲杯组委会邀请甲裁判组派裁判去参加 项活动, 必须有 去, 去 由甲
裁判组 决定, 问甲裁判组共有多少种不同的安排 法
(2) 若亚洲杯组委会安排这 6名裁判担任 6场 赛的主裁判, 每场 赛只有 1名主裁
判,每名裁判只担任 1场 赛的主裁判,根据回避规则, 其中 A不担任第 场 赛的主
裁判,C不担任第三场 赛的主裁判, 问共有多少种不同的安排 法
(3)若亚洲杯组委会将这 6名裁判全部安排到 3项不同的活动中.每项活动 少安排 1
名裁判,每名裁判只参加 1项活动,问共有多少种不同的安排 法
学 科 ( 北 京 ) 股 份 有 限 公 司
21.(本 题满分 12分)已知椭圆 C 的上、 下顶点分别为 A, B,
左顶点为 D, △ABD是 积为 的正三 形。
(1)求椭圆 C的 程;
(2)过椭圆外 点M(m,0)的直线交椭圆于 P, Q两点, 已知点 P与点 P′关于 x轴
对称,直线 与 x轴交于点 K; 若 是钝 ,求 m的取值范围.
22.(本 题满分 12分)已知圆 圆 动
圆 C与这两个圆中的 个内切, 另 个外切.
(1) 求动圆圆 C的轨迹 程.
(2)若动圆圆 C的轨迹为曲线M,D(2,0),斜率不为 0的直线 l与曲线M 交于不同于
D的 A,B 两点, 垂 为点 E,若以 AB为直径的圆经过点 D,试问是否存在定
点 F, 使 为定值 若存在, 求出该定值及 F的坐标;若不存在,请说明理由.
学 科 ( 北 京 ) 股 份 有 限 公 司
数 学 试 卷
考试时 :120分钟, 分值:150分
注意事项:
1. 答题前,考 务必 碳素笔将 的姓名、准考证号、考场号、座位号在答题卡
上填写清楚.
2.每 题选出答案后, 2B铅笔把答题卡上对应题 的答案标号涂 ,如需改动, 橡
擦 净后,再选涂其他答案标号. 在试题卷上作答 效.
第Ⅰ卷(共 60 分)
、选择题:本 题共 8 题,每 题 5分,共 40分.在每 题给出的四个选项中只有
项是符合要求的.
1.抛物线 的焦点坐标是( )
A. (1,0) B. (0,1)
2.设 a∈R, 若直线 :ax+2y-8=0与直线 平 ,则 a的值为( )
A. 1 B. -2 C 1或-2
3.在某城市中,A,B两地有如图所示的 格型道路 ,甲随机沿道路 选择 条最短
路径,从 A地出发去往 B地,途经 C地,则不同的路线有( )
A. 90 种 B. 105 种 C. 260种 D. 315 种
4. 在直三棱柱 中, D,E分别为 AC,BC
的中点,则异 直线 C D与 B E所成 的余弦值为( )
学 科 ( 北 京 ) 股 份 有 限 公 司
5.已知椭圆 E 的右焦点为 F(3,0),过点 F的直线交椭圆 E于 A,
B两点,若 AB的中点坐标为(1,-1), 则椭圆 E的 程为( )
6. 已知圆 C: 与直线 l: mx-y+m+1=0(m≠0),过 l上任意 点 M向圆
C引切线,切点为 A,B, 若 的最 值为 则实数 m的值为( )
7. 如图,已知正 体. 棱 为 1,点 H 在棱 上,且
在侧 内作边 为 的正 形 P是侧 内 动点, 且点 P
到平 距离等于线段 PF的 , 则当点 P运动时, HP 的最 值是( )
8. 数学美的表现形式不同于 然美或艺术美那样直观,它蕴藏于特有的抽象概念,公式
符号,推理论证,思维 法等之中,揭示了规律性,是 种科学的真实美. 平 直 坐标系
中, 曲线 C: 就是 条形状优美的曲线,对于此曲线,给出如下结论:
①曲线 C围成的图形的 积是
②曲线 C围成的图形有 2条对称轴
③ 曲线 C上的任意两点间的距离不超过 2;
④ 若 P(m,n)是曲线 C上任意 点,则 的最 值是
其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
、选择题: 本 题共 4 题, 每 题 5分,共 20分.在每 题给出的选项中, 有多
项符合题 要求,全部选对的得 5分,部分选对的得 2分,有选错的得 0分.
9.给出下列命题, 其中正确的命题是( )
A. 过点(3,4)且在 x,y轴上的截距相等的直线 程为 x-y-7=0
B. 若直线 l的 向向量为 =(1,0,3), 平 α的法向量为 则直线 l//α
C. 点 P(L,1)在圆 内
D. 点 P(x,y)满 则点 P的轨迹是 个椭圆
10. 已 知 圆 与 圆
则( )
学 科 ( 北 京 ) 股 份 有 限 公 司
A. 若圆 C 与 x轴相切, 则 m=±2
B. 若 m=1, 则圆 C 与圆 C 相交
C. 当 时,两圆的公共弦 为
D. 直线 kx-y+3k+2=0与圆 C 始终有两个交点
11.在棱 为 2的正 体 中 ,M是底 ABCD的中 , Q是棱 .
上的 点,且 N为线段 AQ的中点, 则 ( )
A. C, M, N, Q四点共
B. 三棱锥 A-DMN的体积为定值
C. 当 时,过 A,M,Q三点的平 截正 体所得截 的 积为
D. 存在λ使得直线MB 与平 CNQ垂直
12. 如图,已知椭圆 过抛物线 焦点 F的直线交抛物线于M,
N两点,连接NO,MO并延 分别交 C 于A,B两点,连接AB, 与 的 积分
别记为 则在下列结论中正确的为( )
A.若记直线 NO,MO的斜率分别为 则 的 是定值
的 积 是定值
C. 设 则
为定值 5
第Ⅱ卷(共 90分)
三、填空题:本 题共 4 题, 每 题 5分,共 20分.
学 科 ( 北 京 ) 股 份 有 限 公 司
13. 已知空间向量 则向量 在向量 上的投影向量的坐标
是 .
14. 已知 abc表示 个三位数, 如果满 且 那么我们称该三位数为“凸数”,
则没有重复数字的三位“凸数”的个数为 .
15. 如图, 过双曲线 的左焦点 引圆
的切线, 切点为 T, 延 FT交双曲线右 于 P点,M为线段 FP的中
点, O为坐标原点, 若 则双曲线的离 率为 .
16. 空间直 坐标系 xOy中, 过点. 且 个法向量为 的
平 α的 程为 过点 且
向向量为 的直线 l的 程为 阅读上 材料,
并解决下 问题:已知平 α的 程为. 直线 l是两个平 与
的交线,则直线 l与平 α所成 的正弦值为______________
四、解答题:本 题共 6 题,共 70分.解答题应写出必要的 字说明、证明过程或演算步
骤.
17.(本 题满分 10分)
(1)求值:
(2) 解不等式:
学 科 ( 北 京 ) 股 份 有 限 公 司
18.(本 题满分 12分)已知点 A(-1,2)和直线 l:6x-4y+1=0,点 B是点 A关于直线 l的对称点.
(1)求点 B的坐标;
(2)O为坐标原点, 且点 P满 若点 P的轨迹与直线
有公共点,求 m的取值范围.
19.(本 题满分 12分)
三棱柱 中, 线段
的中点为M ,且 BC⊥AM.
(1) 求证:
(2) 点 P在线段 上, 且 求平 与平 夹
的余弦值.
20.(本 题满分 12分)第 18届亚 联亚洲杯将于 2023年举 ,已知此次亚洲杯甲舰判组有
6名裁判,分别是 A、B。C、D、E、F、(以下问题 数字作答)
(1)若亚洲杯组委会邀请甲裁判组派裁判去参加 项活动, 必须有 去, 去 由甲
裁判组 决定, 问甲裁判组共有多少种不同的安排 法
(2) 若亚洲杯组委会安排这 6名裁判担任 6场 赛的主裁判, 每场 赛只有 1名主裁
判,每名裁判只担任 1场 赛的主裁判,根据回避规则, 其中 A不担任第 场 赛的主
裁判,C不担任第三场 赛的主裁判, 问共有多少种不同的安排 法
(3)若亚洲杯组委会将这 6名裁判全部安排到 3项不同的活动中.每项活动 少安排 1
名裁判,每名裁判只参加 1项活动,问共有多少种不同的安排 法
学 科 ( 北 京 ) 股 份 有 限 公 司
21.(本 题满分 12分)已知椭圆 C 的上、 下顶点分别为 A, B,
左顶点为 D, △ABD是 积为 的正三 形。
(1)求椭圆 C的 程;
(2)过椭圆外 点M(m,0)的直线交椭圆于 P, Q两点, 已知点 P与点 P′关于 x轴
对称,直线 与 x轴交于点 K; 若 是钝 ,求 m的取值范围.
22.(本 题满分 12分)已知圆 圆 动
圆 C与这两个圆中的 个内切, 另 个外切.
(1) 求动圆圆 C的轨迹 程.
(2)若动圆圆 C的轨迹为曲线M,D(2,0),斜率不为 0的直线 l与曲线M 交于不同于
D的 A,B 两点, 垂 为点 E,若以 AB为直径的圆经过点 D,试问是否存在定
点 F, 使 为定值 若存在, 求出该定值及 F的坐标;若不存在,请说明理由.
学 科 ( 北 京 ) 股 份 有 限 公 司
同课章节目录
