山东省青岛市市南区2023-2024学年八年级下学期数学期末考试模拟试卷(含答案)
文档属性
| 名称 | 山东省青岛市市南区2023-2024学年八年级下学期数学期末考试模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 239.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 15:17:37 | ||
图片预览

文档简介
山东省青岛市市南区2023-2024学年八年级下学期数学期末考试模拟试卷
综合考试
考试时间:* *分钟 满分:* *分
姓名:__________ 班级:__________考号:__________
题号 一 二 三 总分
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、单选题
得分
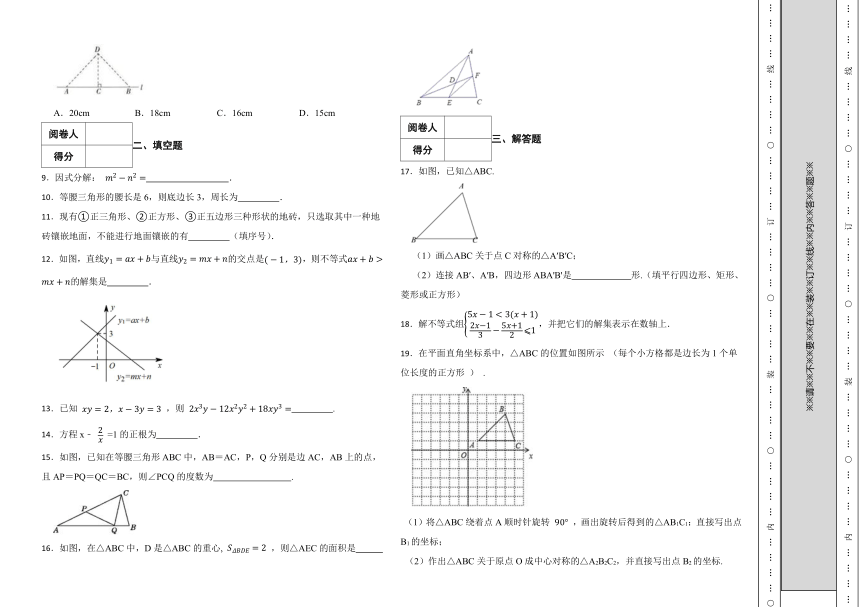
1.有理数a,b在数轴上的对应点如图所示,则下面式子中正确的是( )
A.bC.a b>0 D.a -b> a +b
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
3.下列因式分解正确的是( )
A.4m2-4m+1=4m(m-1) B.a3b2-a2b+a2=a2(ab2-b)
C.x2-7x-10=(x-2)(x-5) D.10x2y-5xy2=5xy(2x-y)
4.如图,在平面直角坐标系中,点 的坐标为 ,以点 为圆心,以 的长为半径画弧,交 轴的负半轴于点 ,则点 的横坐标介于( )
A.-4和-3之间 B.3和4之间 C.-5和-4之间 D.4和5之间
5.如图,正方形 的边长为1,中心为点O,有一边长大小不定的正六边形 绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形 内(包括正方形的边),当这个六边形的边长最大时, 的最小值为( )
A. B. C. D.
6.不等式组 的整数解为( )
A.1 B.0 C.﹣1 D.﹣2
7.化简 的结果是( )
A. B. C. D.
8.如图,长为12cm的橡皮筋放置在直线l上,固定两端A,B,然后把中点C竖直向上拉升8cm至点D处,则拉长后橡皮筋的长为( )
A.20cm B.18cm C.16cm D.15cm
阅卷人 二、填空题
得分
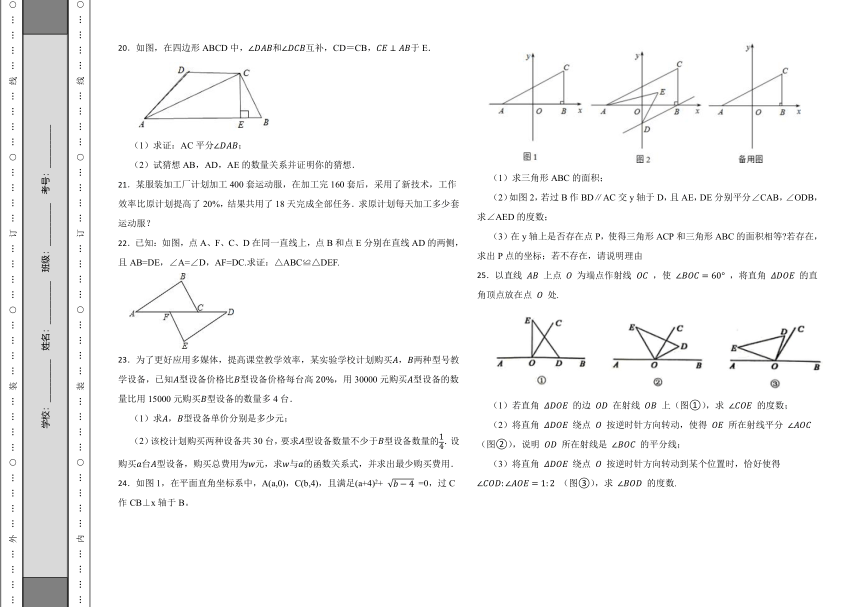
9.因式分解: .
10.等腰三角形的腰长是6,则底边长3,周长为 .
11.现有①正三角形、②正方形、③正五边形三种形状的地砖,只选取其中一种地砖镶嵌地面,不能进行地面镶嵌的有 (填序号).
12.如图,直线与直线的交点是,则不等式的解集是 .
13.已知 ,则 .
14.方程x﹣ =1的正根为 .
15.如图,已知在等腰三角形ABC中,AB=AC,P,Q分别是边AC,AB上的点,且AP=PQ=QC=BC,则∠PCQ的度数为 .
16.如图,在△ABC中,D是△ABC的重心, ,则△AEC的面积是
阅卷人 三、解答题
得分
17.如图,已知△ABC.
(1)画△ABC关于点C对称的△A′B′C;
(2)连接AB′、A′B,四边形ABA'B'是 形.(填平行四边形、矩形、菱形或正方形)
18.解不等式组,并把它们的解集表示在数轴上.
19.在平面直角坐标系中,△ABC的位置如图所示 (每个小方格都是边长为1个单位长度的正方形 ) .
(1)将△ABC绕着点A顺时针旋转 ,画出旋转后得到的△AB1C1;直接写出点B1的坐标;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,并直接写出点B2的坐标.
20.如图,在四边形ABCD中,和互补,CD=CB,于E.
(1)求证:AC平分;
(2)试猜想AB,AD,AE的数量关系并证明你的猜想.
21.某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共用了18天完成全部任务.求原计划每天加工多少套运动服?
22.已知:如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:△ABC≌△DEF.
23.为了更好应用多媒体,提高课堂教学效率,某实验学校计划购买,两种型号教学设备,已知型设备价格比型设备价格每台高,用30000元购买型设备的数量比用15000元购买型设备的数量多4台.
(1)求,型设备单价分别是多少元;
(2)该校计划购买两种设备共30台,要求型设备数量不少于型设备数量的.设购买台型设备,购买总费用为元,求与的函数关系式,并求出最少购买费用.
24.如图1,在平面直角坐标系中,A(a,0),C(b,4),且满足(a+4)2+ =0,过C作CB⊥x轴于B。
(1)求三角形ABC的面积;
(2)如图2,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等 若存在,求出P点的坐标;若不存在,请说明理由
25.以直线 上点 为端点作射线 ,使 ,将直角 的直角顶点放在点 处.
(1)若直角 的边 在射线 上(图①),求 的度数;
(2)将直角 绕点 按逆时针方向转动,使得 所在射线平分 (图②),说明 所在射线是 的平分线;
(3)将直角 绕点 按逆时针方向转动到某个位置时,恰好使得 (图③),求 的度数.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】D
4.【答案】A
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】A
9.【答案】 .
10.【答案】15
11.【答案】③
12.【答案】x>-1
13.【答案】36
14.【答案】x=2
15.【答案】( )°
16.【答案】6
17.【答案】(1)如图,△A′B′C即为所求;
(2)平行四边
18.【答案】解:,
解不等式①得,,
解不等式②得,,
在数轴上表示如下:
所以不等式组的解集为:.
19.【答案】解:如图,B1(4,-2)、B2(-4,-4)
20.【答案】(1)证明:过点C作于F
∵在四边形中
∴
∵
∴
∵,
∴
在和中
∴
∴
∵,
∴平分.
(2)解:
证明:由(1)可得
∴
在和中
∴,
∴
∵,
∴.
21.【答案】解:设原计划每天加工x套运动服,则采用了新技术每天加工(1+20%)x套运动服,
由题意得, + =18,
解得:x=20,
经检验:x=20是原分式方程的解,
答:原计划每天加工20套运动服
22.【答案】解:∵AF=DC,
∴AF+CF=DC+CF,
∴AC=DF,
∵在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS);
23.【答案】(1)解:设每台型设备的价格为元,则每台型号设备的价格为元,
根据题意得,,
解得:.
经检验,是原方程的解.
,
每台型设备的价格为2500元,则每台型号设备的价格为3000元.
(2)解:设购买台型设备,
,
,
,
,
随的增大而增大,
当时,的最小值为(元.
答:最少购买费用为78000元.
24.【答案】(1)解:∵
∴a+4=0,b﹣4=0,
∴a=﹣4,b=4,
∴A(﹣4,0),C(4,4).
∵CB⊥AB,∴B(4,0),
∴AB=8,CB=4,则S三角形ABC= ×8×4=16.
(2)解:如图甲,过E作EF∥AC.
∵CB⊥x轴,
∴CB∥y轴,∠CBA=90°,
∴∠ODB=∠6.
又∵BD∥AC,
∴∠CAB=∠5,
∴∠CAB+∠ODB=∠5+∠6=180°﹣∠CBA=90°.
∵BD∥AC,
∴BD∥AC∥EF,
∴∠1=∠3,∠2=∠4.
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3= ∠CAB,∠4= ∠ODB,
∴∠AED=∠1+∠2=∠3+∠4= (∠CAB+∠ODB)=45°.
(3)解:①当P在y轴正半轴上时,如图乙.
设点P(0,t),分别过点P,A,B作MN∥x轴,AN∥y轴,BM∥y轴,交于点M,N,则AN=t,CM=t﹣4,MN=8,PM=PN=4.
∵S三角形ABC=16,
∴S三角形ACP=S梯形MNAC﹣S三角形ANP﹣S三角形CMP=16,
∴ ×8(t﹣4+t)﹣ ×4t﹣ ×4(t﹣4)=16,解得t=6,即点P的坐标为(0,6).
②当P在y轴负半轴上时,如图丙,同①作辅助线.
设点P(0,a),则AN=﹣a,CM=﹣a+4,PM=PN=4.
∵S三角形ACP=S梯形MNAC﹣S三角形ANP﹣S三角形CMP=16,
∴ ×8(﹣a+4﹣a)﹣ ×4 (﹣a)﹣ ×4(4﹣a)=16,
解得a=﹣2,
∴点P的坐标为(0,﹣2).
综上所述,P点的坐标为(0,﹣2)或(0,6).
25.【答案】(1)解:∵ ,
又∵ ,
∴ .
(2)解:∵ 平分 ,
∴ ,
∵ ,
∴ , ,
∴ ,
∴ 所在直线是 的平分线.
(3)解:设 ,则 ,
∵ , ,
①若∠COD在∠BOC的外部,
∴ ,解得x=10,
∴∠COD=10°,
∴∠BOD=60°+10°=70°;
②若∠COD在∠BOC的内部,
,解得x=30,
∴∠COD=30°,
∴∠BOD=60°-30°=30°;
即 或 ,
∴ 或 .
综合考试
考试时间:* *分钟 满分:* *分
姓名:__________ 班级:__________考号:__________
题号 一 二 三 总分
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、单选题
得分
1.有理数a,b在数轴上的对应点如图所示,则下面式子中正确的是( )
A.b
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
3.下列因式分解正确的是( )
A.4m2-4m+1=4m(m-1) B.a3b2-a2b+a2=a2(ab2-b)
C.x2-7x-10=(x-2)(x-5) D.10x2y-5xy2=5xy(2x-y)
4.如图,在平面直角坐标系中,点 的坐标为 ,以点 为圆心,以 的长为半径画弧,交 轴的负半轴于点 ,则点 的横坐标介于( )
A.-4和-3之间 B.3和4之间 C.-5和-4之间 D.4和5之间
5.如图,正方形 的边长为1,中心为点O,有一边长大小不定的正六边形 绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形 内(包括正方形的边),当这个六边形的边长最大时, 的最小值为( )
A. B. C. D.
6.不等式组 的整数解为( )
A.1 B.0 C.﹣1 D.﹣2
7.化简 的结果是( )
A. B. C. D.
8.如图,长为12cm的橡皮筋放置在直线l上,固定两端A,B,然后把中点C竖直向上拉升8cm至点D处,则拉长后橡皮筋的长为( )
A.20cm B.18cm C.16cm D.15cm
阅卷人 二、填空题
得分
9.因式分解: .
10.等腰三角形的腰长是6,则底边长3,周长为 .
11.现有①正三角形、②正方形、③正五边形三种形状的地砖,只选取其中一种地砖镶嵌地面,不能进行地面镶嵌的有 (填序号).
12.如图,直线与直线的交点是,则不等式的解集是 .
13.已知 ,则 .
14.方程x﹣ =1的正根为 .
15.如图,已知在等腰三角形ABC中,AB=AC,P,Q分别是边AC,AB上的点,且AP=PQ=QC=BC,则∠PCQ的度数为 .
16.如图,在△ABC中,D是△ABC的重心, ,则△AEC的面积是
阅卷人 三、解答题
得分
17.如图,已知△ABC.
(1)画△ABC关于点C对称的△A′B′C;
(2)连接AB′、A′B,四边形ABA'B'是 形.(填平行四边形、矩形、菱形或正方形)
18.解不等式组,并把它们的解集表示在数轴上.
19.在平面直角坐标系中,△ABC的位置如图所示 (每个小方格都是边长为1个单位长度的正方形 ) .
(1)将△ABC绕着点A顺时针旋转 ,画出旋转后得到的△AB1C1;直接写出点B1的坐标;
(2)作出△ABC关于原点O成中心对称的△A2B2C2,并直接写出点B2的坐标.
20.如图,在四边形ABCD中,和互补,CD=CB,于E.
(1)求证:AC平分;
(2)试猜想AB,AD,AE的数量关系并证明你的猜想.
21.某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共用了18天完成全部任务.求原计划每天加工多少套运动服?
22.已知:如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:△ABC≌△DEF.
23.为了更好应用多媒体,提高课堂教学效率,某实验学校计划购买,两种型号教学设备,已知型设备价格比型设备价格每台高,用30000元购买型设备的数量比用15000元购买型设备的数量多4台.
(1)求,型设备单价分别是多少元;
(2)该校计划购买两种设备共30台,要求型设备数量不少于型设备数量的.设购买台型设备,购买总费用为元,求与的函数关系式,并求出最少购买费用.
24.如图1,在平面直角坐标系中,A(a,0),C(b,4),且满足(a+4)2+ =0,过C作CB⊥x轴于B。
(1)求三角形ABC的面积;
(2)如图2,若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ACP和三角形ABC的面积相等 若存在,求出P点的坐标;若不存在,请说明理由
25.以直线 上点 为端点作射线 ,使 ,将直角 的直角顶点放在点 处.
(1)若直角 的边 在射线 上(图①),求 的度数;
(2)将直角 绕点 按逆时针方向转动,使得 所在射线平分 (图②),说明 所在射线是 的平分线;
(3)将直角 绕点 按逆时针方向转动到某个位置时,恰好使得 (图③),求 的度数.
答案解析部分
1.【答案】D
2.【答案】A
3.【答案】D
4.【答案】A
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】A
9.【答案】 .
10.【答案】15
11.【答案】③
12.【答案】x>-1
13.【答案】36
14.【答案】x=2
15.【答案】( )°
16.【答案】6
17.【答案】(1)如图,△A′B′C即为所求;
(2)平行四边
18.【答案】解:,
解不等式①得,,
解不等式②得,,
在数轴上表示如下:
所以不等式组的解集为:.
19.【答案】解:如图,B1(4,-2)、B2(-4,-4)
20.【答案】(1)证明:过点C作于F
∵在四边形中
∴
∵
∴
∵,
∴
在和中
∴
∴
∵,
∴平分.
(2)解:
证明:由(1)可得
∴
在和中
∴,
∴
∵,
∴.
21.【答案】解:设原计划每天加工x套运动服,则采用了新技术每天加工(1+20%)x套运动服,
由题意得, + =18,
解得:x=20,
经检验:x=20是原分式方程的解,
答:原计划每天加工20套运动服
22.【答案】解:∵AF=DC,
∴AF+CF=DC+CF,
∴AC=DF,
∵在△ABC和△DEF中
,
∴△ABC≌△DEF(SAS);
23.【答案】(1)解:设每台型设备的价格为元,则每台型号设备的价格为元,
根据题意得,,
解得:.
经检验,是原方程的解.
,
每台型设备的价格为2500元,则每台型号设备的价格为3000元.
(2)解:设购买台型设备,
,
,
,
,
随的增大而增大,
当时,的最小值为(元.
答:最少购买费用为78000元.
24.【答案】(1)解:∵
∴a+4=0,b﹣4=0,
∴a=﹣4,b=4,
∴A(﹣4,0),C(4,4).
∵CB⊥AB,∴B(4,0),
∴AB=8,CB=4,则S三角形ABC= ×8×4=16.
(2)解:如图甲,过E作EF∥AC.
∵CB⊥x轴,
∴CB∥y轴,∠CBA=90°,
∴∠ODB=∠6.
又∵BD∥AC,
∴∠CAB=∠5,
∴∠CAB+∠ODB=∠5+∠6=180°﹣∠CBA=90°.
∵BD∥AC,
∴BD∥AC∥EF,
∴∠1=∠3,∠2=∠4.
∵AE,DE分别平分∠CAB,∠ODB,
∴∠3= ∠CAB,∠4= ∠ODB,
∴∠AED=∠1+∠2=∠3+∠4= (∠CAB+∠ODB)=45°.
(3)解:①当P在y轴正半轴上时,如图乙.
设点P(0,t),分别过点P,A,B作MN∥x轴,AN∥y轴,BM∥y轴,交于点M,N,则AN=t,CM=t﹣4,MN=8,PM=PN=4.
∵S三角形ABC=16,
∴S三角形ACP=S梯形MNAC﹣S三角形ANP﹣S三角形CMP=16,
∴ ×8(t﹣4+t)﹣ ×4t﹣ ×4(t﹣4)=16,解得t=6,即点P的坐标为(0,6).
②当P在y轴负半轴上时,如图丙,同①作辅助线.
设点P(0,a),则AN=﹣a,CM=﹣a+4,PM=PN=4.
∵S三角形ACP=S梯形MNAC﹣S三角形ANP﹣S三角形CMP=16,
∴ ×8(﹣a+4﹣a)﹣ ×4 (﹣a)﹣ ×4(4﹣a)=16,
解得a=﹣2,
∴点P的坐标为(0,﹣2).
综上所述,P点的坐标为(0,﹣2)或(0,6).
25.【答案】(1)解:∵ ,
又∵ ,
∴ .
(2)解:∵ 平分 ,
∴ ,
∵ ,
∴ , ,
∴ ,
∴ 所在直线是 的平分线.
(3)解:设 ,则 ,
∵ , ,
①若∠COD在∠BOC的外部,
∴ ,解得x=10,
∴∠COD=10°,
∴∠BOD=60°+10°=70°;
②若∠COD在∠BOC的内部,
,解得x=30,
∴∠COD=30°,
∴∠BOD=60°-30°=30°;
即 或 ,
∴ 或 .
同课章节目录
