山东省威海市乳山市2023-2024年七年级上学期期末数学模拟试题(含答案)
文档属性
| 名称 | 山东省威海市乳山市2023-2024年七年级上学期期末数学模拟试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 352.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 15:18:39 | ||
图片预览

文档简介
山东省威海市乳山市2023-2024年七年级上学期期末数学模拟试题
综合考试
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、单选题
得分
1.25的算术平方根是( )
A. 5 B.±5 C.-5 D.±
2.下列四个汽车标志图中,不是轴对称图形的是( )
A. B.
C. D.
3.已知Rt△ABC≌Rt△EDF,Rt△ABC的面积为12,Rt△EDF的一条直角边等于3,则另一直角边的长是( )
A.2 B.4 C.6 D.8
4.一个木工师傅测量了一个等腰三角形木板的腰、底边和高的长,但他把这三个数据与其它的数据弄混了,请你帮助他找出来,是第( )组.
A.13,12,12 B.12,12,8 C.13,10,12 D.5,8,4
5.已知一次函数y=﹣x+m和y=2x+n的图象都经过A(﹣4,0),且与y轴分别交于B、C两点,则△ABC的面积为( )
A.48 B.36 C.24 D.18
6.如图,长方形ABCD是由30个大小相等的正方形拼成的,E、F、G、H分别在AD、 AB、BC、CD边上,且是某个小正方形的顶点,若四边形EFGH的面积为1,则长方形ABCD的面积是( )
A.2 B. C. D.
7.如图,在△ABC中,∠A=90°,AB=AC=2,点O是边BC的中点,半圆O与△ABC相切于点D、E,则阴影部分的面积等于( )
A.1- B. C.1- D.
8.直角三角形的两直角边分别为5厘米、12厘米,则斜边上的高是( )
A.6厘米 B.8厘米 C.厘米 D.厘米
9.如图所示,在正方形网格中有A,B,C三个点,若建立平面直角坐标系后,点A的坐标为(2,1),点B的坐标为(1,﹣2),则点C的坐标为( )
A.(1,1) B.(﹣2,1)
C.(﹣1,﹣2) D.(﹣2,﹣1)
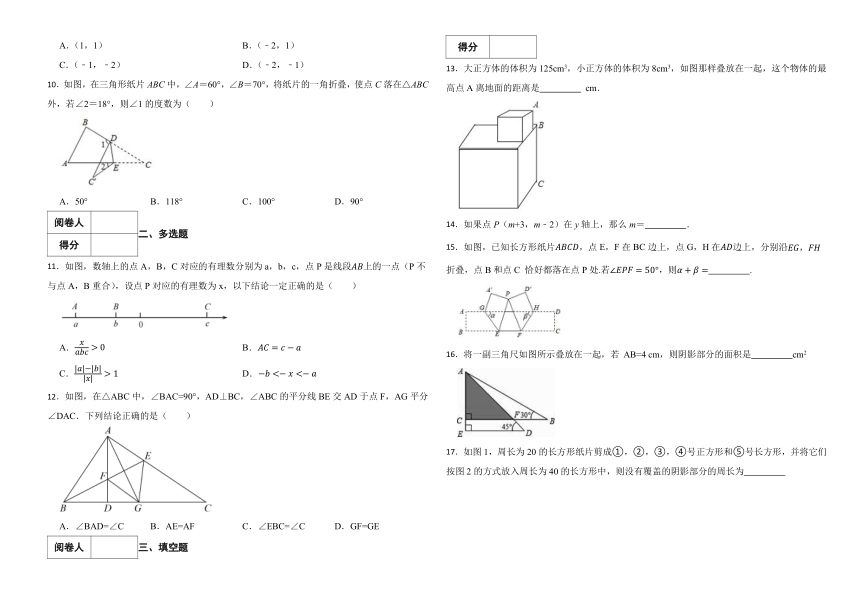
10.如图,在三角形纸片ABC中,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC外,若∠2=18°,则∠1的度数为( )
A.50° B.118° C.100° D.90°
阅卷人 二、多选题
得分
11.如图,数轴上的点A,B,C对应的有理数分别为a,b,c,点P是线段上的一点(P不与点A,B重合),设点P对应的有理数为x,以下结论一定正确的是( )
A. B.
C. D.
12.如图,在△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.下列结论正确的是( )
A.∠BAD=∠C B.AE=AF C.∠EBC=∠C D.GF=GE
阅卷人 三、填空题
得分
13.大正方体的体积为125cm3,小正方体的体积为8cm3,如图那样叠放在一起,这个物体的最高点A离地面的距离是 cm.
14.如果点P(m+3,m﹣2)在y轴上,那么m= .
15.如图,已知长方形纸片,点E,F在BC边上,点G,H在边上,分别沿折叠,点B和点C 恰好都落在点P处.若,则 .
16.将一副三角尺如图所示叠放在一起,若 AB=4 cm,则阴影部分的面积是 cm2
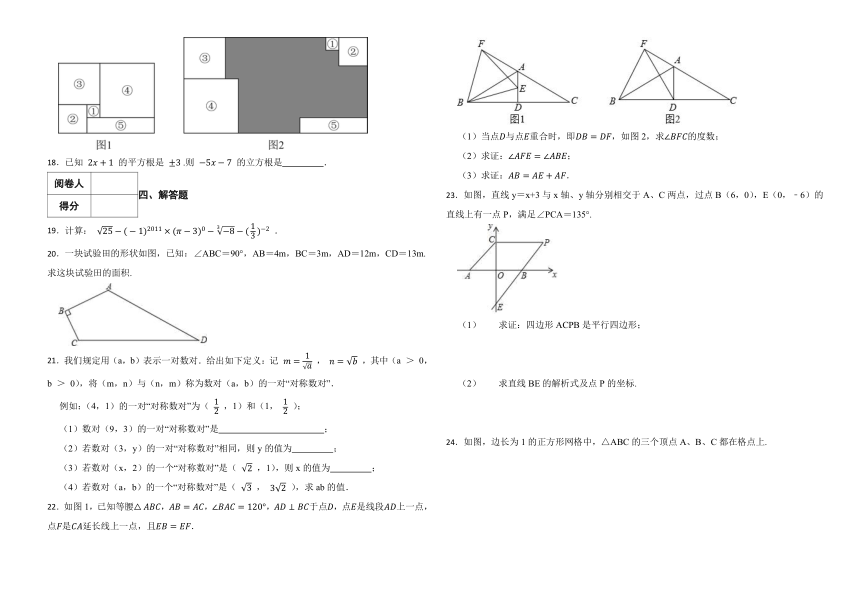
17.如图1,周长为20的长方形纸片剪成①,②,③,④号正方形和⑤号长方形,并将它们按图2的方式放入周长为40的长方形中,则没有覆盖的阴影部分的周长为
18.已知 的平方根是 .则 的立方根是 .
阅卷人 四、解答题
得分
19.计算: .
20.一块试验田的形状如图,已知:∠ABC=90°,AB=4m,BC=3m,AD=12m,CD=13m.求这块试验田的面积.
21.我们规定用(a,b)表示一对数对.给出如下定义:记 , ,其中(a > 0,b > 0),将(m,n)与(n,m)称为数对(a,b)的一对“对称数对”.
例如:(4,1)的一对“对称数对”为( ,1)和(1, );
(1)数对(9,3)的一对“对称数对”是 ;
(2)若数对(3,y)的一对“对称数对”相同,则y的值为 ;
(3)若数对(x,2)的一个“对称数对”是( ,1),则x的值为 ;
(4)若数对(a,b)的一个“对称数对”是( , ),求ab的值.
22.如图1,已知等腰,,,于点,点是线段上一点,点是延长线上一点,且.
(1)当点与点重合时,即,如图2,求的度数;
(2)求证:;
(3)求证:.
23.如图,直线y=x+3与x轴、y轴分别相交于A、C两点,过点B(6,0),E(0,﹣6)的直线上有一点P,满足∠PCA=135°.
(1)
求证:四边形ACPB是平行四边形;
(2)
求直线BE的解析式及点P的坐标.
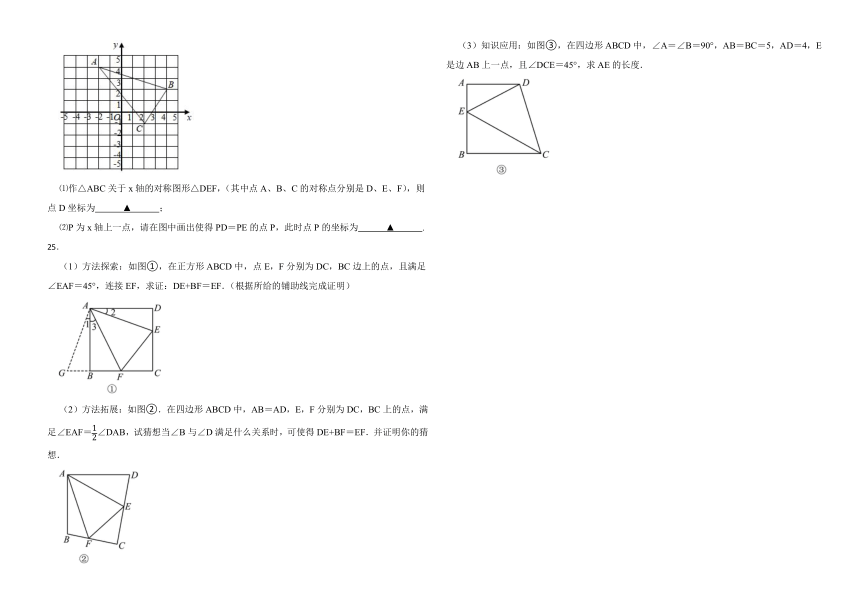
24.如图,边长为1的正方形网格中,△ABC的三个顶点A、B、C都在格点上.
⑴作△ABC关于x轴的对称图形△DEF,(其中点A、B、C的对称点分别是D、E、F),则点D坐标为 ▲ ;
⑵P为x轴上一点,请在图中画出使得PD=PE的点P,此时点P的坐标为 ▲ .
25.
(1)方法探索:如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF.(根据所给的铺助线完成证明)
(2)方法拓展:如图②.在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF=∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.并证明你的猜想.
(3)知识应用:如图③,在四边形ABCD中,∠A=∠B=90°,AB=BC=5,AD=4,E是边AB上一点,且∠DCE=45°,求AE的长度.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
11.【答案】B,D
12.【答案】A,B,D
13.【答案】7
14.【答案】-3
15.【答案】
16.【答案】2
17.【答案】30
18.【答案】-3
19.【答案】解:
=5+1×1+2﹣9
=﹣1.
20.【答案】解:连接AC 根据勾股定理可得:AC=5m∵AD=13m,CD=13m ∴△ACD为直角三角形
∴S=3×4÷2+5×12÷2=6+30=36(平方米)
21.【答案】(1) 与
(2)
(3)1
(4)解:∵数对(a,b)的一对“对称数对”是 与 ,
而数对(a,b)的一个“对称数对”是( , ),
∴① ,解得
∴ ;
② ,解得 ,
∴ ,
综上所述, 或 .
22.【答案】(1)解:如图1,∵AB=AC,∠BAC=120°,
∴∠ACB=∠ABC=30°,
∵AD⊥BC于点D,
∴BD=CD,
∵DB=DF,
∴CD=DF,
∴∠DFC=30°,
∴∠BDF=60°
∵BD=DF,
∴△BDF是等边三角形,
∴∠BFC=90°
(2)证明:∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,
∵AB=AC,AD⊥BC,
∴AD垂直平分BC, 连接EC,则EB=EC,
∴∠EBC=∠ECB, ∵EB=EC, ∴EF=EC,
∴∠EFC=∠ECF,
∴∠AFE+∠EBC=30°,
∵∠ABE+∠EBC=30°,
∴∠AFE=∠ABE;
(3)证明:由(2)知:∠BAE=60°,
∴∠BAD=∠CAD=60°, ∴∠FAE=120°,
∴∠BAF=60°, ∴∠BEF=60°,
∵EB=EF, ∴△BEF为等边三角形,
在边AB上取一点P,使得AP=AF,
∴△APF为等边三角形,
∴∠BFP=∠AFE,∠BPF=∠EAF=120°,PF=AF,
∴△BPF≌△EAF(AAS), ∴BP=AE,
∴AB=BP+PA=AE+AF.
23.【答案】(1)证明:∵直线y=x+3与x轴、y轴分别相交于A、C两点,
∴点A的坐标为(﹣3,0),点C的坐标为(0,3),
∴OA=OC.
∵∠AOC=90°,
∴∠CAO=45°.
∵∠PCA=135°,
∴∠CAO+∠PCA=180°,
∴AB∥CP.
∵点B的坐标为(6,0),点E的坐标为(0,﹣6),
∴OB=OE.
∵∠BOE=90°,
∴∠OBE=45°,
∴∠CAO=∠ABE=45°,
∴AC∥BP,
∴四边形ACPB为平行四边形.
(2)解:设直线BE的解析式为y=kx+b(k≠0), 将B(6,0)、E(0,﹣6)代入y=kx+b,得: ,解得: ∴直线BE的解析式为y=x﹣6. ∵AB∥CP, ∴点P的纵坐标是3, ∴点P的坐标为(9,3).
24.【答案】解:⑴如图所示,△DEF即为所求;D点坐标为(-2,-4),
⑵如图所示;P(0,0),
25.【答案】(1)证明:如图①中,延长CB到点G.使BG=DE.连接AG.
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=∠DAB=∠ABG=90°,
在△ABE和△ADG中,
,
∴△ADE≌△ABG(SAS),
∴AE=AG,∠DAE=∠BAG,
∵∠EAF=45°,
∴∠GAF=∠BAG+∠BAF=∠DAE+∠BAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=BG+BF=DE+BD,
∴EF=DE+BF;
(2)解:当∠ABC+∠D=180°时,结论EF=DE+BF.成立.
理由:如图②中,延长CB到点G.使BG=DE.连接AG.
∵∠ABC+∠D=180°,∠ABC+∠ABG=180°,
∴∠D=∠ABG,
在△ABE和△ADG中,
,
∴△ADE≌△ABG(SAS),
∴AE=AG,∠DAE=∠BAG,
∵∠EAF=∠BAD,
∴∠GAF=∠BAG+∠BAF=∠DAE+∠BAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=BG+BF=DE+BD,
∴EF=DE+BF;
(3)解:如图③中,过点C作CG⊥AD,交AD的延长线于点G.
由(1)知:DE=DG+BE,
设BE=x,则AE=5-x,DE=x+1,
在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,
∴(5-x)2+42=(x+1)2,
解得x=.
∴AE=5-=.
综合考试
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、单选题
得分
1.25的算术平方根是( )
A. 5 B.±5 C.-5 D.±
2.下列四个汽车标志图中,不是轴对称图形的是( )
A. B.
C. D.
3.已知Rt△ABC≌Rt△EDF,Rt△ABC的面积为12,Rt△EDF的一条直角边等于3,则另一直角边的长是( )
A.2 B.4 C.6 D.8
4.一个木工师傅测量了一个等腰三角形木板的腰、底边和高的长,但他把这三个数据与其它的数据弄混了,请你帮助他找出来,是第( )组.
A.13,12,12 B.12,12,8 C.13,10,12 D.5,8,4
5.已知一次函数y=﹣x+m和y=2x+n的图象都经过A(﹣4,0),且与y轴分别交于B、C两点,则△ABC的面积为( )
A.48 B.36 C.24 D.18
6.如图,长方形ABCD是由30个大小相等的正方形拼成的,E、F、G、H分别在AD、 AB、BC、CD边上,且是某个小正方形的顶点,若四边形EFGH的面积为1,则长方形ABCD的面积是( )
A.2 B. C. D.
7.如图,在△ABC中,∠A=90°,AB=AC=2,点O是边BC的中点,半圆O与△ABC相切于点D、E,则阴影部分的面积等于( )
A.1- B. C.1- D.
8.直角三角形的两直角边分别为5厘米、12厘米,则斜边上的高是( )
A.6厘米 B.8厘米 C.厘米 D.厘米
9.如图所示,在正方形网格中有A,B,C三个点,若建立平面直角坐标系后,点A的坐标为(2,1),点B的坐标为(1,﹣2),则点C的坐标为( )
A.(1,1) B.(﹣2,1)
C.(﹣1,﹣2) D.(﹣2,﹣1)
10.如图,在三角形纸片ABC中,∠A=60°,∠B=70°,将纸片的一角折叠,使点C落在△ABC外,若∠2=18°,则∠1的度数为( )
A.50° B.118° C.100° D.90°
阅卷人 二、多选题
得分
11.如图,数轴上的点A,B,C对应的有理数分别为a,b,c,点P是线段上的一点(P不与点A,B重合),设点P对应的有理数为x,以下结论一定正确的是( )
A. B.
C. D.
12.如图,在△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.下列结论正确的是( )
A.∠BAD=∠C B.AE=AF C.∠EBC=∠C D.GF=GE
阅卷人 三、填空题
得分
13.大正方体的体积为125cm3,小正方体的体积为8cm3,如图那样叠放在一起,这个物体的最高点A离地面的距离是 cm.
14.如果点P(m+3,m﹣2)在y轴上,那么m= .
15.如图,已知长方形纸片,点E,F在BC边上,点G,H在边上,分别沿折叠,点B和点C 恰好都落在点P处.若,则 .
16.将一副三角尺如图所示叠放在一起,若 AB=4 cm,则阴影部分的面积是 cm2
17.如图1,周长为20的长方形纸片剪成①,②,③,④号正方形和⑤号长方形,并将它们按图2的方式放入周长为40的长方形中,则没有覆盖的阴影部分的周长为
18.已知 的平方根是 .则 的立方根是 .
阅卷人 四、解答题
得分
19.计算: .
20.一块试验田的形状如图,已知:∠ABC=90°,AB=4m,BC=3m,AD=12m,CD=13m.求这块试验田的面积.
21.我们规定用(a,b)表示一对数对.给出如下定义:记 , ,其中(a > 0,b > 0),将(m,n)与(n,m)称为数对(a,b)的一对“对称数对”.
例如:(4,1)的一对“对称数对”为( ,1)和(1, );
(1)数对(9,3)的一对“对称数对”是 ;
(2)若数对(3,y)的一对“对称数对”相同,则y的值为 ;
(3)若数对(x,2)的一个“对称数对”是( ,1),则x的值为 ;
(4)若数对(a,b)的一个“对称数对”是( , ),求ab的值.
22.如图1,已知等腰,,,于点,点是线段上一点,点是延长线上一点,且.
(1)当点与点重合时,即,如图2,求的度数;
(2)求证:;
(3)求证:.
23.如图,直线y=x+3与x轴、y轴分别相交于A、C两点,过点B(6,0),E(0,﹣6)的直线上有一点P,满足∠PCA=135°.
(1)
求证:四边形ACPB是平行四边形;
(2)
求直线BE的解析式及点P的坐标.
24.如图,边长为1的正方形网格中,△ABC的三个顶点A、B、C都在格点上.
⑴作△ABC关于x轴的对称图形△DEF,(其中点A、B、C的对称点分别是D、E、F),则点D坐标为 ▲ ;
⑵P为x轴上一点,请在图中画出使得PD=PE的点P,此时点P的坐标为 ▲ .
25.
(1)方法探索:如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证:DE+BF=EF.(根据所给的铺助线完成证明)
(2)方法拓展:如图②.在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF=∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.并证明你的猜想.
(3)知识应用:如图③,在四边形ABCD中,∠A=∠B=90°,AB=BC=5,AD=4,E是边AB上一点,且∠DCE=45°,求AE的长度.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】D
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
11.【答案】B,D
12.【答案】A,B,D
13.【答案】7
14.【答案】-3
15.【答案】
16.【答案】2
17.【答案】30
18.【答案】-3
19.【答案】解:
=5+1×1+2﹣9
=﹣1.
20.【答案】解:连接AC 根据勾股定理可得:AC=5m∵AD=13m,CD=13m ∴△ACD为直角三角形
∴S=3×4÷2+5×12÷2=6+30=36(平方米)
21.【答案】(1) 与
(2)
(3)1
(4)解:∵数对(a,b)的一对“对称数对”是 与 ,
而数对(a,b)的一个“对称数对”是( , ),
∴① ,解得
∴ ;
② ,解得 ,
∴ ,
综上所述, 或 .
22.【答案】(1)解:如图1,∵AB=AC,∠BAC=120°,
∴∠ACB=∠ABC=30°,
∵AD⊥BC于点D,
∴BD=CD,
∵DB=DF,
∴CD=DF,
∴∠DFC=30°,
∴∠BDF=60°
∵BD=DF,
∴△BDF是等边三角形,
∴∠BFC=90°
(2)证明:∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,
∵AB=AC,AD⊥BC,
∴AD垂直平分BC, 连接EC,则EB=EC,
∴∠EBC=∠ECB, ∵EB=EC, ∴EF=EC,
∴∠EFC=∠ECF,
∴∠AFE+∠EBC=30°,
∵∠ABE+∠EBC=30°,
∴∠AFE=∠ABE;
(3)证明:由(2)知:∠BAE=60°,
∴∠BAD=∠CAD=60°, ∴∠FAE=120°,
∴∠BAF=60°, ∴∠BEF=60°,
∵EB=EF, ∴△BEF为等边三角形,
在边AB上取一点P,使得AP=AF,
∴△APF为等边三角形,
∴∠BFP=∠AFE,∠BPF=∠EAF=120°,PF=AF,
∴△BPF≌△EAF(AAS), ∴BP=AE,
∴AB=BP+PA=AE+AF.
23.【答案】(1)证明:∵直线y=x+3与x轴、y轴分别相交于A、C两点,
∴点A的坐标为(﹣3,0),点C的坐标为(0,3),
∴OA=OC.
∵∠AOC=90°,
∴∠CAO=45°.
∵∠PCA=135°,
∴∠CAO+∠PCA=180°,
∴AB∥CP.
∵点B的坐标为(6,0),点E的坐标为(0,﹣6),
∴OB=OE.
∵∠BOE=90°,
∴∠OBE=45°,
∴∠CAO=∠ABE=45°,
∴AC∥BP,
∴四边形ACPB为平行四边形.
(2)解:设直线BE的解析式为y=kx+b(k≠0), 将B(6,0)、E(0,﹣6)代入y=kx+b,得: ,解得: ∴直线BE的解析式为y=x﹣6. ∵AB∥CP, ∴点P的纵坐标是3, ∴点P的坐标为(9,3).
24.【答案】解:⑴如图所示,△DEF即为所求;D点坐标为(-2,-4),
⑵如图所示;P(0,0),
25.【答案】(1)证明:如图①中,延长CB到点G.使BG=DE.连接AG.
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=∠DAB=∠ABG=90°,
在△ABE和△ADG中,
,
∴△ADE≌△ABG(SAS),
∴AE=AG,∠DAE=∠BAG,
∵∠EAF=45°,
∴∠GAF=∠BAG+∠BAF=∠DAE+∠BAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=BG+BF=DE+BD,
∴EF=DE+BF;
(2)解:当∠ABC+∠D=180°时,结论EF=DE+BF.成立.
理由:如图②中,延长CB到点G.使BG=DE.连接AG.
∵∠ABC+∠D=180°,∠ABC+∠ABG=180°,
∴∠D=∠ABG,
在△ABE和△ADG中,
,
∴△ADE≌△ABG(SAS),
∴AE=AG,∠DAE=∠BAG,
∵∠EAF=∠BAD,
∴∠GAF=∠BAG+∠BAF=∠DAE+∠BAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=BG+BF=DE+BD,
∴EF=DE+BF;
(3)解:如图③中,过点C作CG⊥AD,交AD的延长线于点G.
由(1)知:DE=DG+BE,
设BE=x,则AE=5-x,DE=x+1,
在Rt△ADE中,由勾股定理得:AD2+AE2=DE2,
∴(5-x)2+42=(x+1)2,
解得x=.
∴AE=5-=.
同课章节目录
