山东省烟台市招远市2023-2024学年七年级下学期数学期末考试模拟试卷(五四学制)(含答案)
文档属性
| 名称 | 山东省烟台市招远市2023-2024学年七年级下学期数学期末考试模拟试卷(五四学制)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 198.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 00:00:00 | ||
图片预览



文档简介
山东省烟台市招远市2023-2024学年七年级下学期数学期末考试
模拟试卷(五四学制)
综合考试
考试时间:* *分钟 满分:* *分
姓名:__________ 班级:__________考号:__________
题号 一 二 三 总分
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
得分
1.设a,b为实数,下面四个命题.
①若a>b, 则a2>b2 ②若a2>b2, 则a>b
③若>, 则a2>b2 ④若a2>b2 则>
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.下列说法: ①把弯曲的河道改直,能够缩短航程,这是由于两点之间线段最短; ②若线段AC=BC,则点C是线段AB的中点;③射线AB与射线AD是同一条射线;④ 连结两点的线段叫做这两点的距离;⑤将一根细木条固定在墙上,至少需要两根钉子,是因为两点确定一条直线.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
3.下列说法中正确的是( )
A.两个直角三角形全等
B.两个等腰三角形全等
C.两个等边三角形全等
D.两条直角边对应相等的直角三角形全等
4.满足关于x的不等式组 恰有二个整数解,a的取值范围为( )
A.-15.如图,AB∥CD,AD平分∠BAC,∠C=80°,则∠D的度数为( )。
A.50° B.55° C.70° D.80°
6.如图, 表示北偏东 方向的一条射线, 表示南偏西 方向的一条射线,则 的度数是( )
A. B. C. D.
7.已知方程组,若用“加减法”消去y,下列做法正确的是( )
A.①+② B.①+②×2 C.①-② D.①-②×2
8.某同学这学期前四次数学测验的成绩依次为93、82、76和88,马上要进行第五次数学测验了,她这五次成绩的平均数能够达到或超过85分,那么,这次测验她的分数至少是( )
A.83 B.84 C.85 D.86
9.如图,直线y=kx+b交坐标轴于A(﹣5,0),B(0,7)两点,则不等式kx+b>0的解集是( )
A.x<﹣5 B.x>﹣5 C.x>7 D.x<﹣7
10.如图,在 中, , ,以 为圆心,任意长为半径画弧分别交 、 于点 和 ,再分别以 、 为圆心,大于 的长为半径画弧,两弧交于点 ,连结 并延长交 于点 ,则下列说法中正确的个数是( )
① 是 的平分线;② ;③ ;④
A.1 B.2 C.3 D.4
阅卷人 二、填空题(本大题共6小题,共18.0分)
得分
11.x的与2的差为正数,用不等式表示为 .
12.一条有破损的长方形纸带,按如图折叠,纸带重部分中的∠α的度数为 .
13.如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AB于D,交AC于E,且EC=5,则AE的长为 .
14.关于x的分式方程的解为正数,且关于的不等式组的解集为,则所有满足条件的整数的值之和是 .
15.已知斜边长为20,一条直角边长为12,该直角三角形斜边上的高为 .
16.不等式组 的解集是
阅卷人 三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
得分
17.解不等式组 ,将解集在数轴上表示出来,并求出此不等式组的所有整数解.
18.如图,已知∠AOB和点M、N,求作点 使P到∠AOB两边的距离相等且PM=PN.
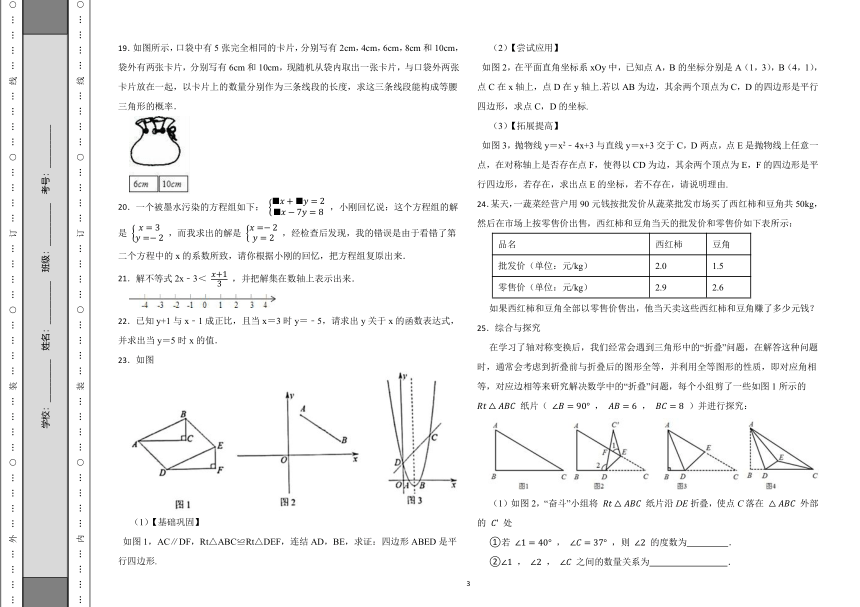
19.如图所示,口袋中有5张完全相同的卡片,分别写有2cm,4cm,6cm,8cm和10cm,袋外有两张卡片,分别写有6cm和10cm,现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,求这三条线段能构成等腰三角形的概率.
20.一个被墨水污染的方程组如下: ,小刚回忆说:这个方程组的解是 ,而我求出的解是 ,经检查后发现,我的错误是由于看错了第二个方程中的x的系数所致,请你根据小刚的回忆,把方程组复原出来.
21.解不等式2x﹣3< ,并把解集在数轴上表示出来.
22.已知y+1与x﹣1成正比,且当x=3时y=﹣5,请求出y关于x的函数表达式,并求出当y=5时x的值.
23.如图
(1)【基础巩固】
如图1,AC∥DF,Rt△ABC≌Rt△DEF,连结AD,BE,求证:四边形ABED是平行四边形.
(2)【尝试应用】
如图2,在平面直角坐标系xOy中,已知点A,B的坐标分别是A(1,3),B(4,1),点C在x轴上,点D在y轴上.若以AB为边,其余两个顶点为C,D的四边形是平行四边形,求点C,D的坐标.
(3)【拓展提高】
如图3,抛物线y=x2﹣4x+3与直线y=x+3交于C,D两点,点E是抛物线上任意一点,在对称轴上是否存在点F,使得以CD为边,其余两个顶点为E,F的四边形是平行四边形,若存在,求出点E的坐标,若不存在,请说明理由.
24.某天,一蔬菜经营户用90元钱按批发价从蔬菜批发市场买了西红柿和豆角共50kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如下表所示:
品名 西红柿 豆角
批发价(单位:元/kg) 2.0 1.5
零售价(单位:元/kg) 2.9 2.6
如果西红柿和豆角全部以零售价售出,他当天卖这些西红柿和豆角赚了多少元钱?
25.综合与探究
在学习了轴对称变换后,我们经常会遇到三角形中的“折叠”问题,在解答这种问题时,通常会考虑到折叠前与折叠后的图形全等,并利用全等图形的性质,即对应角相等,对应边相等来研究解决数学中的“折叠”问题,每个小组剪了一些如图1所示的 纸片( , , )并进行探究:
(1)如图2,“奋斗”小组将 纸片沿DE折叠,使点C落在 外部的 处
①若 , ,则 的度数为 .
② , , 之间的数量关系为 .
(2)如图3,“勤奋”小组将 沿DE折叠,使点C与点A重合,求BD的长;
(3)如图4,“雄鹰”小组将 沿AD折叠,使点B落在点E处,连接CE,当 为直角三角形时,求BD的长.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】C
11.【答案】>0
12.【答案】75°
13.【答案】10
14.【答案】13
15.【答案】9.6
16.【答案】﹣1≤x<3
17.【答案】解:解不等式 ,得
解不等式 ,得
则不等式组的解集为
在数轴上表示如下:
此不等式组的整数解为 ,0,1.
18.【答案】解:如图,作∠AOB的平分线OC,线段MN的垂直平分线EF,直线EF与射线OC的交点即为所求的点P.
19.【答案】解:共有5种可能的结果数,它们是:2、6、10;4、6、10;6、6、10;8、6、10;10、6、10,
其中这三条线段能构成等腰三角形的结果数2种,分别是6、6、10和10、6、10,
所以这三条线段能构成等腰三角形的概率是 .
20.【答案】解:设被滴上墨水的方程组为 ,
由小刚所说,知 和 都是原方程组中第一个方程ax+by=2的解,
则有 ,
解之,得 .
又因方程组的解是 ,
所以3m+14=8,
m=﹣2.
故所求方程组为
21.【答案】解:先去分母,得3(2x﹣3)<x+1
去括号,得6x﹣9<x+1
移项,得5x<10
系数化为1,得x<2
∴原不等式的解集为:x<2,
在数轴上表示为:
22.【答案】解:依题意,设y+1=k(x﹣1)(k≠0),将x=3,y=﹣5代入,
得到:﹣5+1=k(3﹣1),
解得:k=﹣2.
所以y+1=﹣2(x﹣1),即y=﹣2x+1.
令y=5,解得x=﹣2
23.【答案】(1)证明:∵AC∥DF,
∴∠CAD+∠ADF=180°,
∵Rt△ABC≌Rt△DEF,
∴∠BAC=∠EDF,AB=DE,
∴∠BAD+∠ADE=180°,
∴AB∥DE,
∴四边形ABED是平行四边形;
(2)解:当点C、D都在坐标轴正半轴时,如图,过点A作AM⊥y轴于M,过点B作BN⊥x轴于N,连接AC,
∵AM∥ON,
∴∠MAC=∠ACN,
∵AD∥BC,∴∠DAC=∠ACB,
∴∠MAD=∠BCN,
在△AMD与△BCN中,
,
∴△AMD≌△BCN(AAS),
∴AM=CN=1,MD=BN=1,
∴OD=2,OC=3,
∴C(3,0),D(0,2);
当点C、D都在坐标轴负半轴时,如图,过点A作AP⊥x轴于P,过点B作BQ⊥y轴于Q,
同理可证△APC≌△DQB(AAS),
∴AP=QD=3,CP=BQ=4,
∴OD=2,OC=3,
∴C(-3,0),D(0,-2);
综上,点C,D的坐标为C(3,0),D(0,2)或C(-3,0),D(0,-2);
(3)解:存在,理由如下:
解方程组,得或,
∴C(5,8),D(0,3),
抛物线y=x2﹣4x+3的对称轴为,
∵以CD为边,其余两个顶点为E,F的四边形是平行四边形,
显然,点E,F在边CD的上方,
设E(m,),D(2,n),
当DE为对角线时,则D、E与F、C的中点坐标相同,
则,
解得:,
则,
∴E(7,24);
当DF为对角线时,则D、F与E、C的中点坐标相同,
则,
解得:,
则,
∴E(-3,24);
综上,点E的坐标为(-3,24)或(7,24).
24.【答案】解:设购进西红柿xkg,购进豆角ykg,
根据题意得: ,
解得: ,
∴(2.9-2)x+(2.6-1.5)y=49.
答:他当天卖这些西红柿和豆角赚了49元钱.
25.【答案】(1)114°;∠2=∠1+2∠C
(2)解:∵ , ,
设BD=x,则CD=AD=8-x
∴在Rt△ABD中, ,解得:
∴BD的长为
(3)解:在Rt△ABC中,∠ABC=90°,AB=6,BC=8,
∴AC= =10,
∵△AED是△ABD以AD为折痕翻折得到的,
∴AE=AB=6,DE=BD,∠AED=∠B=90°.
当△DEC为直角三角形,
①如图,当∠DEC=90°时,
∵∠AED+∠DEC=180°,
∴点E在线段AC上,
设BD=DE=x,则CD=8-x,
∴CE=AC-AE=4,
∴DE2+CE2=CD2,
即x2+42=(8-x)2,
解得:x=3,即BD=3;
②如图,当∠EDC=90°,
∴∠BDE=90°,
∵∠BDA=∠ADE,
∴∠BDA=∠ADE=45°,
∴∠BAD=45°,
∴AB=BD=6.
综上所述:当△DEC为直角三角形时,BD的长为3或6.
模拟试卷(五四学制)
综合考试
考试时间:* *分钟 满分:* *分
姓名:__________ 班级:__________考号:__________
题号 一 二 三 总分
评分
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 xx 分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
得分
1.设a,b为实数,下面四个命题.
①若a>b, 则a2>b2 ②若a2>b2, 则a>b
③若>, 则a2>b2 ④若a2>b2 则>
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
2.下列说法: ①把弯曲的河道改直,能够缩短航程,这是由于两点之间线段最短; ②若线段AC=BC,则点C是线段AB的中点;③射线AB与射线AD是同一条射线;④ 连结两点的线段叫做这两点的距离;⑤将一根细木条固定在墙上,至少需要两根钉子,是因为两点确定一条直线.其中说法正确的有( )
A.1个 B.2个 C.3个 D.4个
3.下列说法中正确的是( )
A.两个直角三角形全等
B.两个等腰三角形全等
C.两个等边三角形全等
D.两条直角边对应相等的直角三角形全等
4.满足关于x的不等式组 恰有二个整数解,a的取值范围为( )
A.-1
A.50° B.55° C.70° D.80°
6.如图, 表示北偏东 方向的一条射线, 表示南偏西 方向的一条射线,则 的度数是( )
A. B. C. D.
7.已知方程组,若用“加减法”消去y,下列做法正确的是( )
A.①+② B.①+②×2 C.①-② D.①-②×2
8.某同学这学期前四次数学测验的成绩依次为93、82、76和88,马上要进行第五次数学测验了,她这五次成绩的平均数能够达到或超过85分,那么,这次测验她的分数至少是( )
A.83 B.84 C.85 D.86
9.如图,直线y=kx+b交坐标轴于A(﹣5,0),B(0,7)两点,则不等式kx+b>0的解集是( )
A.x<﹣5 B.x>﹣5 C.x>7 D.x<﹣7
10.如图,在 中, , ,以 为圆心,任意长为半径画弧分别交 、 于点 和 ,再分别以 、 为圆心,大于 的长为半径画弧,两弧交于点 ,连结 并延长交 于点 ,则下列说法中正确的个数是( )
① 是 的平分线;② ;③ ;④
A.1 B.2 C.3 D.4
阅卷人 二、填空题(本大题共6小题,共18.0分)
得分
11.x的与2的差为正数,用不等式表示为 .
12.一条有破损的长方形纸带,按如图折叠,纸带重部分中的∠α的度数为 .
13.如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线交AB于D,交AC于E,且EC=5,则AE的长为 .
14.关于x的分式方程的解为正数,且关于的不等式组的解集为,则所有满足条件的整数的值之和是 .
15.已知斜边长为20,一条直角边长为12,该直角三角形斜边上的高为 .
16.不等式组 的解集是
阅卷人 三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
得分
17.解不等式组 ,将解集在数轴上表示出来,并求出此不等式组的所有整数解.
18.如图,已知∠AOB和点M、N,求作点 使P到∠AOB两边的距离相等且PM=PN.
19.如图所示,口袋中有5张完全相同的卡片,分别写有2cm,4cm,6cm,8cm和10cm,袋外有两张卡片,分别写有6cm和10cm,现随机从袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,求这三条线段能构成等腰三角形的概率.
20.一个被墨水污染的方程组如下: ,小刚回忆说:这个方程组的解是 ,而我求出的解是 ,经检查后发现,我的错误是由于看错了第二个方程中的x的系数所致,请你根据小刚的回忆,把方程组复原出来.
21.解不等式2x﹣3< ,并把解集在数轴上表示出来.
22.已知y+1与x﹣1成正比,且当x=3时y=﹣5,请求出y关于x的函数表达式,并求出当y=5时x的值.
23.如图
(1)【基础巩固】
如图1,AC∥DF,Rt△ABC≌Rt△DEF,连结AD,BE,求证:四边形ABED是平行四边形.
(2)【尝试应用】
如图2,在平面直角坐标系xOy中,已知点A,B的坐标分别是A(1,3),B(4,1),点C在x轴上,点D在y轴上.若以AB为边,其余两个顶点为C,D的四边形是平行四边形,求点C,D的坐标.
(3)【拓展提高】
如图3,抛物线y=x2﹣4x+3与直线y=x+3交于C,D两点,点E是抛物线上任意一点,在对称轴上是否存在点F,使得以CD为边,其余两个顶点为E,F的四边形是平行四边形,若存在,求出点E的坐标,若不存在,请说明理由.
24.某天,一蔬菜经营户用90元钱按批发价从蔬菜批发市场买了西红柿和豆角共50kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如下表所示:
品名 西红柿 豆角
批发价(单位:元/kg) 2.0 1.5
零售价(单位:元/kg) 2.9 2.6
如果西红柿和豆角全部以零售价售出,他当天卖这些西红柿和豆角赚了多少元钱?
25.综合与探究
在学习了轴对称变换后,我们经常会遇到三角形中的“折叠”问题,在解答这种问题时,通常会考虑到折叠前与折叠后的图形全等,并利用全等图形的性质,即对应角相等,对应边相等来研究解决数学中的“折叠”问题,每个小组剪了一些如图1所示的 纸片( , , )并进行探究:
(1)如图2,“奋斗”小组将 纸片沿DE折叠,使点C落在 外部的 处
①若 , ,则 的度数为 .
② , , 之间的数量关系为 .
(2)如图3,“勤奋”小组将 沿DE折叠,使点C与点A重合,求BD的长;
(3)如图4,“雄鹰”小组将 沿AD折叠,使点B落在点E处,连接CE,当 为直角三角形时,求BD的长.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】A
6.【答案】D
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】C
11.【答案】>0
12.【答案】75°
13.【答案】10
14.【答案】13
15.【答案】9.6
16.【答案】﹣1≤x<3
17.【答案】解:解不等式 ,得
解不等式 ,得
则不等式组的解集为
在数轴上表示如下:
此不等式组的整数解为 ,0,1.
18.【答案】解:如图,作∠AOB的平分线OC,线段MN的垂直平分线EF,直线EF与射线OC的交点即为所求的点P.
19.【答案】解:共有5种可能的结果数,它们是:2、6、10;4、6、10;6、6、10;8、6、10;10、6、10,
其中这三条线段能构成等腰三角形的结果数2种,分别是6、6、10和10、6、10,
所以这三条线段能构成等腰三角形的概率是 .
20.【答案】解:设被滴上墨水的方程组为 ,
由小刚所说,知 和 都是原方程组中第一个方程ax+by=2的解,
则有 ,
解之,得 .
又因方程组的解是 ,
所以3m+14=8,
m=﹣2.
故所求方程组为
21.【答案】解:先去分母,得3(2x﹣3)<x+1
去括号,得6x﹣9<x+1
移项,得5x<10
系数化为1,得x<2
∴原不等式的解集为:x<2,
在数轴上表示为:
22.【答案】解:依题意,设y+1=k(x﹣1)(k≠0),将x=3,y=﹣5代入,
得到:﹣5+1=k(3﹣1),
解得:k=﹣2.
所以y+1=﹣2(x﹣1),即y=﹣2x+1.
令y=5,解得x=﹣2
23.【答案】(1)证明:∵AC∥DF,
∴∠CAD+∠ADF=180°,
∵Rt△ABC≌Rt△DEF,
∴∠BAC=∠EDF,AB=DE,
∴∠BAD+∠ADE=180°,
∴AB∥DE,
∴四边形ABED是平行四边形;
(2)解:当点C、D都在坐标轴正半轴时,如图,过点A作AM⊥y轴于M,过点B作BN⊥x轴于N,连接AC,
∵AM∥ON,
∴∠MAC=∠ACN,
∵AD∥BC,∴∠DAC=∠ACB,
∴∠MAD=∠BCN,
在△AMD与△BCN中,
,
∴△AMD≌△BCN(AAS),
∴AM=CN=1,MD=BN=1,
∴OD=2,OC=3,
∴C(3,0),D(0,2);
当点C、D都在坐标轴负半轴时,如图,过点A作AP⊥x轴于P,过点B作BQ⊥y轴于Q,
同理可证△APC≌△DQB(AAS),
∴AP=QD=3,CP=BQ=4,
∴OD=2,OC=3,
∴C(-3,0),D(0,-2);
综上,点C,D的坐标为C(3,0),D(0,2)或C(-3,0),D(0,-2);
(3)解:存在,理由如下:
解方程组,得或,
∴C(5,8),D(0,3),
抛物线y=x2﹣4x+3的对称轴为,
∵以CD为边,其余两个顶点为E,F的四边形是平行四边形,
显然,点E,F在边CD的上方,
设E(m,),D(2,n),
当DE为对角线时,则D、E与F、C的中点坐标相同,
则,
解得:,
则,
∴E(7,24);
当DF为对角线时,则D、F与E、C的中点坐标相同,
则,
解得:,
则,
∴E(-3,24);
综上,点E的坐标为(-3,24)或(7,24).
24.【答案】解:设购进西红柿xkg,购进豆角ykg,
根据题意得: ,
解得: ,
∴(2.9-2)x+(2.6-1.5)y=49.
答:他当天卖这些西红柿和豆角赚了49元钱.
25.【答案】(1)114°;∠2=∠1+2∠C
(2)解:∵ , ,
设BD=x,则CD=AD=8-x
∴在Rt△ABD中, ,解得:
∴BD的长为
(3)解:在Rt△ABC中,∠ABC=90°,AB=6,BC=8,
∴AC= =10,
∵△AED是△ABD以AD为折痕翻折得到的,
∴AE=AB=6,DE=BD,∠AED=∠B=90°.
当△DEC为直角三角形,
①如图,当∠DEC=90°时,
∵∠AED+∠DEC=180°,
∴点E在线段AC上,
设BD=DE=x,则CD=8-x,
∴CE=AC-AE=4,
∴DE2+CE2=CD2,
即x2+42=(8-x)2,
解得:x=3,即BD=3;
②如图,当∠EDC=90°,
∴∠BDE=90°,
∵∠BDA=∠ADE,
∴∠BDA=∠ADE=45°,
∴∠BAD=45°,
∴AB=BD=6.
综上所述:当△DEC为直角三角形时,BD的长为3或6.
同课章节目录
