19.1.1变量与函数课件
文档属性
| 名称 | 19.1.1变量与函数课件 |  | |
| 格式 | zip | ||
| 文件大小 | 474.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-02 10:05:34 | ||
图片预览










文档简介
课件35张PPT。人教实验版变量与函数19.1.1 汽车以60千米/时的速度匀速行驶,行驶里程
为 s 千米,行驶时间为 t 小时,填下面的表:说说你是如何得到的:路程 = 速度×时间试用含t的 式子表示 sS = 60t60120180240300问题一问题二 每张电影票的售价为10元,如果早场售出票150张,
日场售出205张,晚场售出310张,三场电影票的票房
收入各多少元?早场票房收入 = 10×150 = 1500 (元)日场票房收入 = 10×205 = 2050 (元)晚场票房收入 = 10×310 = 3100 (元) 若设一场电影售出票 x 张,票房收入为 y 元,
怎样用含 x 的式子表示 y ? y = 10x请说明道理:票房收入 = 售价×售票张数 在一根弹簧的下端挂重物,改变并记录重物的质量,
观察并记录弹簧长度的变化,探索它们的变化规律。如
果弹簧原长为10cm,每1千克重物使弹簧伸长0.5cm,
怎样用含重物质量x(单位:kg)的式子表示受力后的
弹簧长度 L(单位:cm)?挂重2千克时弹簧长=10+0.5×2=11(cm)挂重3千克时弹簧长=10+0.5×3=11.5(cm)挂重x千克时弹簧长=10+0.5×x (cm)L=10+0.5x分析:挂重1千克时弹簧长=10+0.5×1=10.5(cm)问题三问题四用10 m 长的绳子围成长方形,长方形的长为 3m时面积为多少?当长方形的长为3时,面积 =3×(10-2×3)÷2 = 6各组讨论:改变长方形的长,观察长方形的面积怎样变化?设长方形的长为 x m,面积为S m2,怎样用含x的式子表示 s ?S=x(10-2x)÷2剖析S = 60ty = 10xL=10+0.5x变量:在一个变化过程中,数值发生变化的量为变量。常量:在一个变化过程中,数值始终不变的量为常量。请指出上面各个变化过程中的常量、变量。八年级 数学探究:指出下列关系式中的变量与常量:(1) y = 5x -6(2) y= (3) y= 4x2+5x-7(4) S = Лr2解:(1)5和-6是常量,x和y是变量。(2)6是常量,x、y是变量。(3)4、5、-7是常量,x、y是变量。(4)兀是常量,s、r是变量。填空:
1、计划购买50元的乒乓球,所能购买的总数
n(个)与单价 a(元)的关系式为 。
其中的变量是 ,常量是 。
2、某位教师为学生购买数学辅导书,书的单价是4元,
则总金额y(元)与学生数n(个)的关系式是 。其中的变量是 。常量是 。n、a50y=4ny、n4巩固练习快速抢答八年级 数学2、如图2正方体的棱长为a,表面积S= ,
体积V= .C= 4x6a2a31、如图1正方形的周长与边长为x的关系式为变量是: 常量是: ;c、x4练习一:
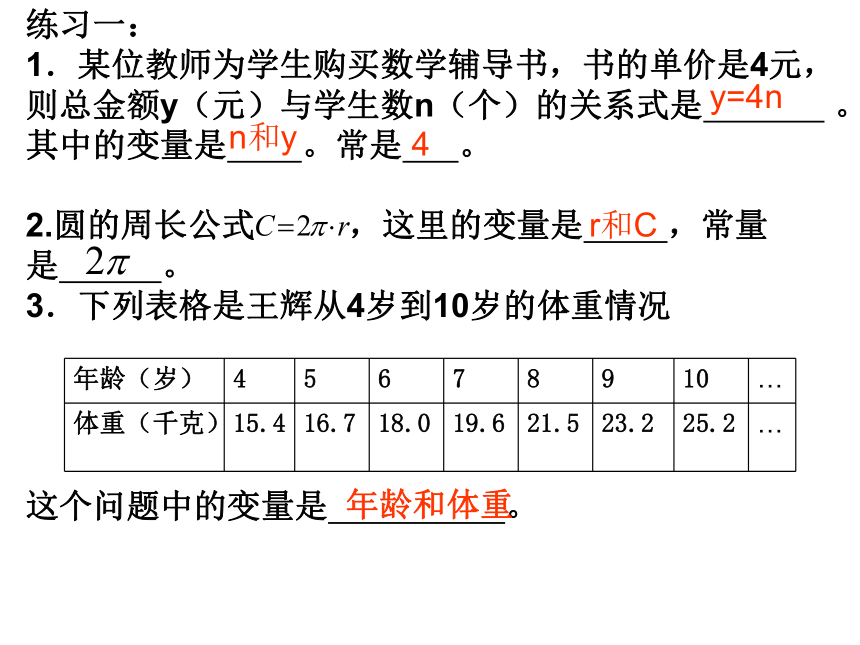
1.某位教师为学生购买数学辅导书,书的单价是4元,则总金额y(元)与学生数n(个)的关系式是 。其中的变量是 。常是 。
2.圆的周长公式 ,这里的变量是 ,常量是 。
3.下列表格是王辉从4岁到10岁的体重情况
这个问题中的变量是 。y=4nn和y4r和C年龄和体重4.1361015 y、n 汽车以60千米/时的速度匀速行驶,行驶里程
为 s 千米,行驶时间为 t 小时,填下面的表:有两个变量,当行驶时间t取定一个数值时,
行驶里程s就随之确定一个值。如当t=1时,s=60。60120180240300问题一在问题一中,是否各有两个变量?同一 个问题中的变量之间有什么联系?S = 60t问题二 每张电影票的售价为10元,如果早场售出票150张,
日场售出205张,晚场售出310张,三场电影票的票房
收入各多少元? y = 10x有两个变量,当售票数量x取定一个数值时,
票房收入y就随之确定一个值。如当x=150时,y=1500。在问题二中,是否各有两个变量?同一 个问题中的变量之间有什么联系?若设一场电影售出票 x张,票房收入
为 y 元,怎样用含 x 的式子表示 y ?
在一根弹簧的下端挂重物,改变并记录重物的质量,
观察并记录弹簧长度的变化,探索它们的变化规律。如
果弹簧长原长为10cm,每1千克重物使弹簧伸长0.5cm,
怎样用含重物质量x(单位:kg)的式子表示受力后的
弹簧长度 L(单位:cm)?L=10+0.5x问题三有两个变量,当中午质量x取定一个数值时,
弹簧长度L就随之确定一个值。如当x=1时,L=10.5。在问题三中,是否各有两个变量?同一 个问题中的变量之间有什么联系?问题四设长方形的边长为 x m,面积为S m2,怎样用含x的式子表示 s ?有两个变量,当长方形的长x取定一个数值时,
面积s就随之确定一个值。在问题四中,是否各有两个变量?同一 个问题中的变量之间有什么联系?在一个变化过程中,如果有两个变量x与y,并且对于x 的一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值。问题 观察中时间x是自变量,心脏电流y是x的函数人口数统计表中,年份x是自变量,人口数是y是x函数,x=1999使的函数值y=12.52亿 例如在问题1中,时间t是自变量,
里程s是t的函数。t=1时,其函数值为60,
t=2时,其函数值为120。(1) xy=2;
(3) x+y=5;
(5) y=x2-4x+5(2) x2+y2=10;
(4) |y|=x;
(6) y= |x|
指出下列变化关系中,哪些y是x的函数,哪些不是?说出你的理由。是否是是否是该你显身手了!例: 一个三角形的底边为5,高h可以任意伸缩,三角形的面积也随之发生了变化.
解:(1)面积s随高h变化的关系式s = ,
其中常量是 ,变量是 , 是自变量, 是 的函数;
(2)当h=3时,面积s=______,
(3)当h=10时,面积s=______;h和shsh7.525练习二
购买一些签字笔,单价3元,总价为y元,签字笔为x支,根据题意填表:
(1)y随x变化的关系式y= , 是自变量,
是 的函数;
(2)当购买8支签字笔时,总价为 元.
2.一个梯形的上底是4,下底是9,写出面积S随高h变化的函数关系式 ,常量是 ,变量是 ,
自变量是 , 是 的函数。3693xxyx24h和shsh3.小张准备将平时的零用钱节约一些储存起来.他已存有50元,从现在起每个月节存12元.设x个月后小张的存款数为y,试写出小张的存款数与从现在开始的月份数之间的函数关系式 ,其中常量是 ,变量是
,自变量是 , 是 的函数。y=50+12x50,12x,yxyx4.请同学们找出这些函数的常量、变量、自变量和函数:
(1) y =3000-300x (2) S=570-95t (3) y=x (4) 解:(1)常量是3000,-300;变量是x,y;自变量是x;y是x的函数。
(2)常量是570,-95;变量是t,s;自变量是t;s是t的函数。
(3)常量是1;变量是x,y;自变量是x;y是x的函数。
(4)常量是 ;变量是r,s;自变量是r;s是r的函数。5.如图是体检时的心电图,其中图上的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,这个问题的变量是 ,
是 的函数。x和yyx思考题:
填表并回答问题:
(1)对于x的每一个值,y都有唯一的值与之对应吗?答: 。
(2)y是x的函数吗?为什么?2和-28和-818和-1832和-32不是答:不是,因为y的值不是唯一的。 例1、写出下列各问题中的关系式,并指出其中的自变量与函数。(1)正方形的面积S 随边长 x 的变化(2)秀水村的耕地面积是106m2,这个村人均耕地面积y随着人数的变化而变化(3)正多边形的内角和度数y随变数n的变化情况 S=x2y= (n-2) ×180°例2B课堂练习D错误,请再想想。ABCDA2错误,请再想想。ABCD 1、下面各题中分别有几个变量?你能将其中某个变量看成是另一个变量的函数吗?为什么?如果能,请写出它们的关系式。(1)每一个同学购一本代数书,书的单价为2元,则 x 个同学共付 y 元。(2)计划购买50元的乒乓球,则所购的总数 y(个)与单价 x (元)的关系。(3)一个铜球在0 ℃的体积为1000cm3,加热后温度每增加1℃,体积增加0.051cm3,t ℃时球的体积为 V cm3 。解: y 是 x 的函数.其关系式为: y = 2x (x ≥0)解: y 是 x 的函数,其关系式为: y =(X>0)解: v是 t 的函数,其关系式为: v = 0.051t+1000探究与讨论(1)在计算器上按照下面的程序进行操作:711-35207问题:显示的数y是x的函数吗?为什么? 一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。(1)写出表示y与x的函数关系的式子。(2)指出自变量x的取值范围(3)汽车行驶200 km时,油箱中还有多少油?解:(1) 函数关系式为: y = 50-0.1x(2) 由x≥0及50-0.1x ≥0 得 0 ≤ x ≤ 500
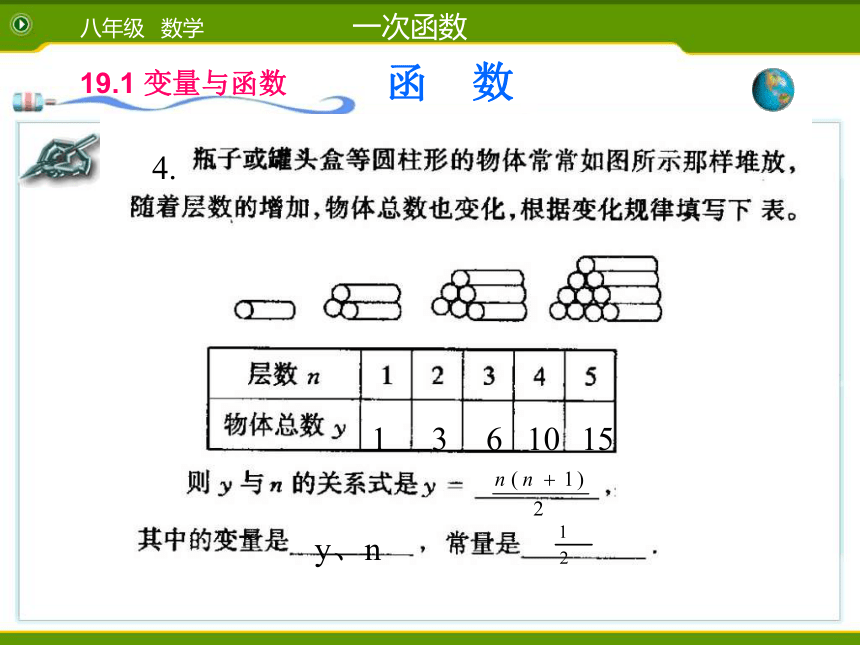
∴自变量的取值范围是: 0 ≤ x ≤ 500(3)当 x = 200时,函数 y 的值为:y=50-0.1×200=30因此,当汽车行驶200 km时,油箱中还有油30L例1、求出下列函数中自变量的取值范围(1)y=2x解: 自变量 x 的取值范围:x为任何实数解: 由n-1≥0得n≥1 ∴自变量 n 的取值范围: n≥1解:由x+2 ≠ 0得 x≠-2 ∴自变量 n 的取值范围: x≠-2解:自变量的取值范围是: k≤1且k ≠-1y=2x+15X≥1且为整数 x ≠ -1解:∵花盆图案形如三角形,每边花有n个,总共有3n个,
其中重复了算3个。
∴ s 与 n 的函数关系式为: s = 3n-3 4、节约资源是当前最热门的话题,我市居民每月用电不超过100度时,按0.57元/度计算;超过100度电时,其中不超过100度部分按0.57元/度计算,超过部分按0.8元/度计算.(1)如果小聪家每月用电x(x≥100)度,请写出(2)若小明家8月份用了125度电,则应缴电费少?(3)若小华家七月份缴电费45.6元,则该月用电多少度? 电费y 与用电量x的函数关系式。解:电费y与用电量x的函数式为:y = 0.8(x-100)+57 (x≥100)解:当x=125时,y = 0.8×(125-100)+57 = 77
∴应缴电费77元。解:∵缴电费小于57元
∴电费y与用电量x的关系式为: y=0.57x
由 45.6 = 0.57x 得x=80 因此该月用电80度。
为 s 千米,行驶时间为 t 小时,填下面的表:说说你是如何得到的:路程 = 速度×时间试用含t的 式子表示 sS = 60t60120180240300问题一问题二 每张电影票的售价为10元,如果早场售出票150张,
日场售出205张,晚场售出310张,三场电影票的票房
收入各多少元?早场票房收入 = 10×150 = 1500 (元)日场票房收入 = 10×205 = 2050 (元)晚场票房收入 = 10×310 = 3100 (元) 若设一场电影售出票 x 张,票房收入为 y 元,
怎样用含 x 的式子表示 y ? y = 10x请说明道理:票房收入 = 售价×售票张数 在一根弹簧的下端挂重物,改变并记录重物的质量,
观察并记录弹簧长度的变化,探索它们的变化规律。如
果弹簧原长为10cm,每1千克重物使弹簧伸长0.5cm,
怎样用含重物质量x(单位:kg)的式子表示受力后的
弹簧长度 L(单位:cm)?挂重2千克时弹簧长=10+0.5×2=11(cm)挂重3千克时弹簧长=10+0.5×3=11.5(cm)挂重x千克时弹簧长=10+0.5×x (cm)L=10+0.5x分析:挂重1千克时弹簧长=10+0.5×1=10.5(cm)问题三问题四用10 m 长的绳子围成长方形,长方形的长为 3m时面积为多少?当长方形的长为3时,面积 =3×(10-2×3)÷2 = 6各组讨论:改变长方形的长,观察长方形的面积怎样变化?设长方形的长为 x m,面积为S m2,怎样用含x的式子表示 s ?S=x(10-2x)÷2剖析S = 60ty = 10xL=10+0.5x变量:在一个变化过程中,数值发生变化的量为变量。常量:在一个变化过程中,数值始终不变的量为常量。请指出上面各个变化过程中的常量、变量。八年级 数学探究:指出下列关系式中的变量与常量:(1) y = 5x -6(2) y= (3) y= 4x2+5x-7(4) S = Лr2解:(1)5和-6是常量,x和y是变量。(2)6是常量,x、y是变量。(3)4、5、-7是常量,x、y是变量。(4)兀是常量,s、r是变量。填空:
1、计划购买50元的乒乓球,所能购买的总数
n(个)与单价 a(元)的关系式为 。
其中的变量是 ,常量是 。
2、某位教师为学生购买数学辅导书,书的单价是4元,
则总金额y(元)与学生数n(个)的关系式是 。其中的变量是 。常量是 。n、a50y=4ny、n4巩固练习快速抢答八年级 数学2、如图2正方体的棱长为a,表面积S= ,
体积V= .C= 4x6a2a31、如图1正方形的周长与边长为x的关系式为变量是: 常量是: ;c、x4练习一:
1.某位教师为学生购买数学辅导书,书的单价是4元,则总金额y(元)与学生数n(个)的关系式是 。其中的变量是 。常是 。
2.圆的周长公式 ,这里的变量是 ,常量是 。
3.下列表格是王辉从4岁到10岁的体重情况
这个问题中的变量是 。y=4nn和y4r和C年龄和体重4.1361015 y、n 汽车以60千米/时的速度匀速行驶,行驶里程
为 s 千米,行驶时间为 t 小时,填下面的表:有两个变量,当行驶时间t取定一个数值时,
行驶里程s就随之确定一个值。如当t=1时,s=60。60120180240300问题一在问题一中,是否各有两个变量?同一 个问题中的变量之间有什么联系?S = 60t问题二 每张电影票的售价为10元,如果早场售出票150张,
日场售出205张,晚场售出310张,三场电影票的票房
收入各多少元? y = 10x有两个变量,当售票数量x取定一个数值时,
票房收入y就随之确定一个值。如当x=150时,y=1500。在问题二中,是否各有两个变量?同一 个问题中的变量之间有什么联系?若设一场电影售出票 x张,票房收入
为 y 元,怎样用含 x 的式子表示 y ?
在一根弹簧的下端挂重物,改变并记录重物的质量,
观察并记录弹簧长度的变化,探索它们的变化规律。如
果弹簧长原长为10cm,每1千克重物使弹簧伸长0.5cm,
怎样用含重物质量x(单位:kg)的式子表示受力后的
弹簧长度 L(单位:cm)?L=10+0.5x问题三有两个变量,当中午质量x取定一个数值时,
弹簧长度L就随之确定一个值。如当x=1时,L=10.5。在问题三中,是否各有两个变量?同一 个问题中的变量之间有什么联系?问题四设长方形的边长为 x m,面积为S m2,怎样用含x的式子表示 s ?有两个变量,当长方形的长x取定一个数值时,
面积s就随之确定一个值。在问题四中,是否各有两个变量?同一 个问题中的变量之间有什么联系?在一个变化过程中,如果有两个变量x与y,并且对于x 的一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值。问题 观察中时间x是自变量,心脏电流y是x的函数人口数统计表中,年份x是自变量,人口数是y是x函数,x=1999使的函数值y=12.52亿 例如在问题1中,时间t是自变量,
里程s是t的函数。t=1时,其函数值为60,
t=2时,其函数值为120。(1) xy=2;
(3) x+y=5;
(5) y=x2-4x+5(2) x2+y2=10;
(4) |y|=x;
(6) y= |x|
指出下列变化关系中,哪些y是x的函数,哪些不是?说出你的理由。是否是是否是该你显身手了!例: 一个三角形的底边为5,高h可以任意伸缩,三角形的面积也随之发生了变化.
解:(1)面积s随高h变化的关系式s = ,
其中常量是 ,变量是 , 是自变量, 是 的函数;
(2)当h=3时,面积s=______,
(3)当h=10时,面积s=______;h和shsh7.525练习二
购买一些签字笔,单价3元,总价为y元,签字笔为x支,根据题意填表:
(1)y随x变化的关系式y= , 是自变量,
是 的函数;
(2)当购买8支签字笔时,总价为 元.
2.一个梯形的上底是4,下底是9,写出面积S随高h变化的函数关系式 ,常量是 ,变量是 ,
自变量是 , 是 的函数。3693xxyx24h和shsh3.小张准备将平时的零用钱节约一些储存起来.他已存有50元,从现在起每个月节存12元.设x个月后小张的存款数为y,试写出小张的存款数与从现在开始的月份数之间的函数关系式 ,其中常量是 ,变量是
,自变量是 , 是 的函数。y=50+12x50,12x,yxyx4.请同学们找出这些函数的常量、变量、自变量和函数:
(1) y =3000-300x (2) S=570-95t (3) y=x (4) 解:(1)常量是3000,-300;变量是x,y;自变量是x;y是x的函数。
(2)常量是570,-95;变量是t,s;自变量是t;s是t的函数。
(3)常量是1;变量是x,y;自变量是x;y是x的函数。
(4)常量是 ;变量是r,s;自变量是r;s是r的函数。5.如图是体检时的心电图,其中图上的横坐标x表示时间,纵坐标y表示心脏部位的生物电流,这个问题的变量是 ,
是 的函数。x和yyx思考题:
填表并回答问题:
(1)对于x的每一个值,y都有唯一的值与之对应吗?答: 。
(2)y是x的函数吗?为什么?2和-28和-818和-1832和-32不是答:不是,因为y的值不是唯一的。 例1、写出下列各问题中的关系式,并指出其中的自变量与函数。(1)正方形的面积S 随边长 x 的变化(2)秀水村的耕地面积是106m2,这个村人均耕地面积y随着人数的变化而变化(3)正多边形的内角和度数y随变数n的变化情况 S=x2y= (n-2) ×180°例2B课堂练习D错误,请再想想。ABCDA2错误,请再想想。ABCD 1、下面各题中分别有几个变量?你能将其中某个变量看成是另一个变量的函数吗?为什么?如果能,请写出它们的关系式。(1)每一个同学购一本代数书,书的单价为2元,则 x 个同学共付 y 元。(2)计划购买50元的乒乓球,则所购的总数 y(个)与单价 x (元)的关系。(3)一个铜球在0 ℃的体积为1000cm3,加热后温度每增加1℃,体积增加0.051cm3,t ℃时球的体积为 V cm3 。解: y 是 x 的函数.其关系式为: y = 2x (x ≥0)解: y 是 x 的函数,其关系式为: y =(X>0)解: v是 t 的函数,其关系式为: v = 0.051t+1000探究与讨论(1)在计算器上按照下面的程序进行操作:711-35207问题:显示的数y是x的函数吗?为什么? 一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km。(1)写出表示y与x的函数关系的式子。(2)指出自变量x的取值范围(3)汽车行驶200 km时,油箱中还有多少油?解:(1) 函数关系式为: y = 50-0.1x(2) 由x≥0及50-0.1x ≥0 得 0 ≤ x ≤ 500
∴自变量的取值范围是: 0 ≤ x ≤ 500(3)当 x = 200时,函数 y 的值为:y=50-0.1×200=30因此,当汽车行驶200 km时,油箱中还有油30L例1、求出下列函数中自变量的取值范围(1)y=2x解: 自变量 x 的取值范围:x为任何实数解: 由n-1≥0得n≥1 ∴自变量 n 的取值范围: n≥1解:由x+2 ≠ 0得 x≠-2 ∴自变量 n 的取值范围: x≠-2解:自变量的取值范围是: k≤1且k ≠-1y=2x+15X≥1且为整数 x ≠ -1解:∵花盆图案形如三角形,每边花有n个,总共有3n个,
其中重复了算3个。
∴ s 与 n 的函数关系式为: s = 3n-3 4、节约资源是当前最热门的话题,我市居民每月用电不超过100度时,按0.57元/度计算;超过100度电时,其中不超过100度部分按0.57元/度计算,超过部分按0.8元/度计算.(1)如果小聪家每月用电x(x≥100)度,请写出(2)若小明家8月份用了125度电,则应缴电费少?(3)若小华家七月份缴电费45.6元,则该月用电多少度? 电费y 与用电量x的函数关系式。解:电费y与用电量x的函数式为:y = 0.8(x-100)+57 (x≥100)解:当x=125时,y = 0.8×(125-100)+57 = 77
∴应缴电费77元。解:∵缴电费小于57元
∴电费y与用电量x的关系式为: y=0.57x
由 45.6 = 0.57x 得x=80 因此该月用电80度。
