数学人教A版(2019)必修第一1.1集合的概念 课件(共35张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一1.1集合的概念 课件(共35张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 08:51:13 | ||
图片预览









文档简介
(共35张PPT)
1.1集合的概念
二 新课讲解
问题1:如何简洁、准确地表述数学对象及研究范围呢?
1、集合的概念
一般地,我们把研究对象统称为元素(element),把一些元素组成的总体叫做集合(set)(简称为集).
表示方法:
一般采用大写英文字母A,B,C,…表示集合
小写英文字母a,b,c,… 表示集合的元素.
它们都是集合吗?
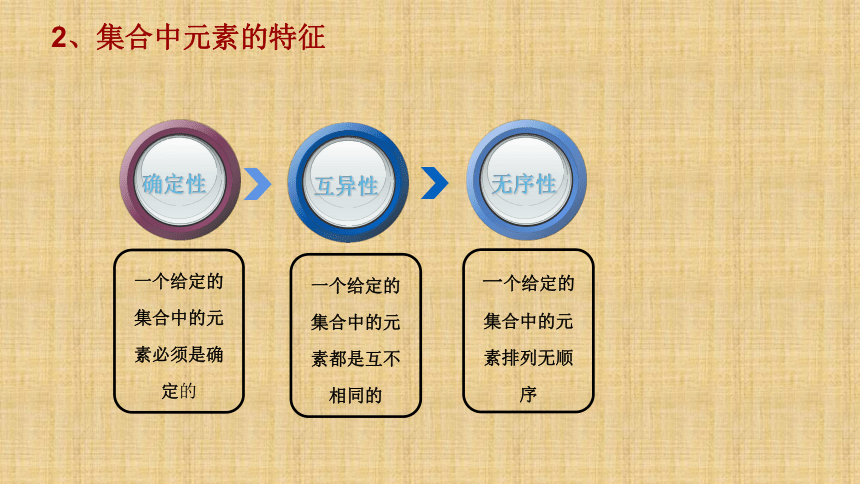
2、集合中元素的特征
无序性
一个给定的 集合中的元
素排列无顺
序
确定性
一个给定的集合中的元素必须是确定的
互异性
一个给定的集合中的元素都是互不相同的
议一议
小组合作探究——集合元素的特征:
任意一组对象是否都能组成一个集合?集合中的元素有什么特征?
问题1:某单位所有的“跑得快的人”能否构成一个集合?
由此说明什么?
问题2:在一个给定的集合中能否有相同的元素?
由此说明了什么?
不能、集合中的元素是不重复出现的
问题3:咱班的全体同学组成一个集合,打乱座位后这个集合有没有变化?
由此说明什么?
没有,集合中的元素是没有顺序的
不能、集合中的元素必须是确定的
典型例题
例1:2019年9月,我们踏入了心仪的高中校园,找到了自己的班级.则下列对象中能构成一个集合的是哪些?并说明你的理由.
(1)你所在班级中的全体同学;
(2)班级中比较高的同学;
(3)班级中身高超过178 cm的同学;
(4)班级中比较胖的同学;
(5)班级中体重超过75 kg的同学;
(6)学习成绩比较好的同学
班级中的全体同学是确定的,所以可以构成一个集合
因为“比较高”无法衡量,所以对象不确定,所以不能构成一个集合
因为“身高超过178 cm”是确定的,所以可以构成一个集合
“比较胖”无法衡量,所以对象不确定,所以不能构成一个集合
“体重超过75 kg”是确定的,所以可以构成一个集合.
“学习成绩比较好”无法衡量,所以对象不确定,所以不能构成一个集合
3、常用数集及其记法
由数组成的集合叫数集
元素与集合
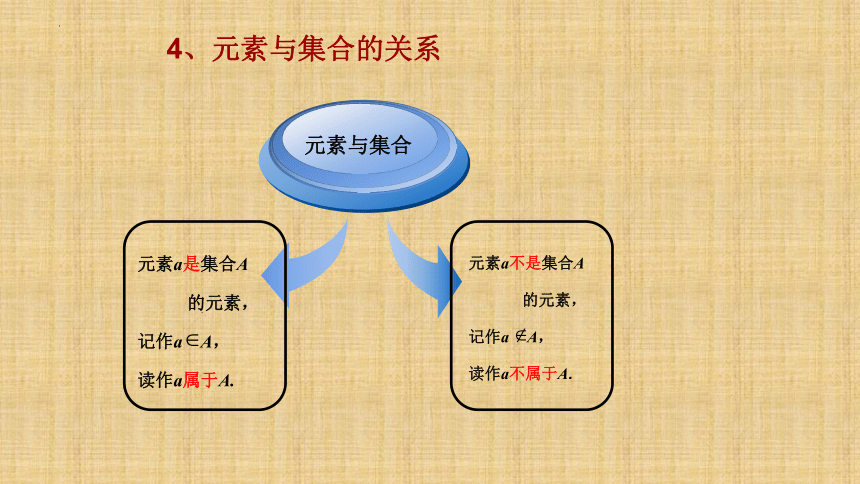
4、元素与集合的关系
.
元素a是集合A
的元素,
记作a A,
读作a属于A.
元素a不是集合A
的元素,
记作a A,
读作a不属于A.
典型例题
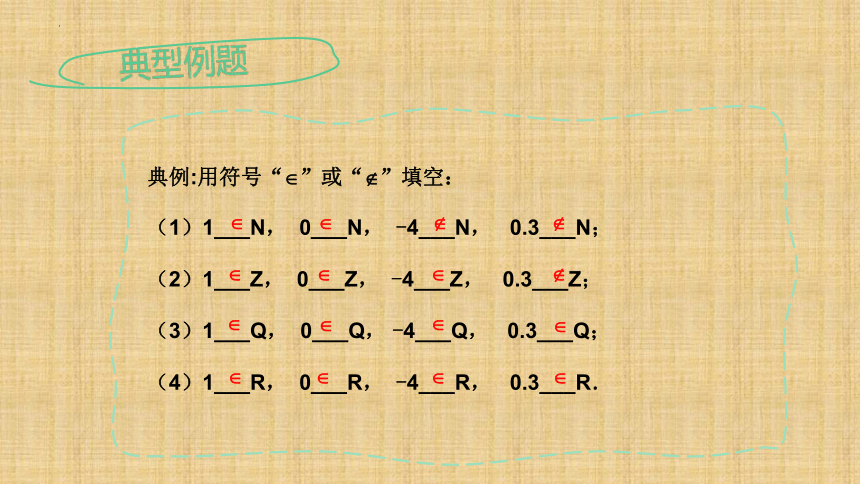
典例:用符号“ ”或“ ”填空:
(1)1___N, 0___N, -4___N, 0.3___N;
(2)1___Z, 0___Z, -4___Z, 0.3___Z;
(3)1___Q, 0___Q, -4___Q, 0.3___Q;
(4)1___R, 0___R, -4___R, 0.3___R.
典型例题
变式2: 用符号“ ”或“ ”填空:
(1)-3___N; (2) 3.14___ Q;
(3) ___Z; (4) - ___R;
(5) ___R; (6) 0 ___Z.
典型例题
×
√
√
×
√
√
(1)有限集:
含有有限个元素的集合
(2)无限集:
含有无限个元素的集合
不含任何元素的集合
叫做空集记作
6、集合的分类
5、集合的相等
例1:
(3)
练习
练习
追问2:当集合中元素个数有无数个,我们如何表示呢?
追问4:你能用描述法表示偶数集吗?
追问5:我们如何用描述法表示有理数集?
追问3:整数集Z可以分为奇数集和偶数集.我们如何用描述法表示奇数集?
练习
(5)Venn图(图示法)
(6)区间表示法(连续的数集)
课堂小结
这节课我们学习了元素和集合的含义,元素与集合的“属于”关系及用符号语言刻画集合.
1.1集合的概念
二 新课讲解
问题1:如何简洁、准确地表述数学对象及研究范围呢?
1、集合的概念
一般地,我们把研究对象统称为元素(element),把一些元素组成的总体叫做集合(set)(简称为集).
表示方法:
一般采用大写英文字母A,B,C,…表示集合
小写英文字母a,b,c,… 表示集合的元素.
它们都是集合吗?
2、集合中元素的特征
无序性
一个给定的 集合中的元
素排列无顺
序
确定性
一个给定的集合中的元素必须是确定的
互异性
一个给定的集合中的元素都是互不相同的
议一议
小组合作探究——集合元素的特征:
任意一组对象是否都能组成一个集合?集合中的元素有什么特征?
问题1:某单位所有的“跑得快的人”能否构成一个集合?
由此说明什么?
问题2:在一个给定的集合中能否有相同的元素?
由此说明了什么?
不能、集合中的元素是不重复出现的
问题3:咱班的全体同学组成一个集合,打乱座位后这个集合有没有变化?
由此说明什么?
没有,集合中的元素是没有顺序的
不能、集合中的元素必须是确定的
典型例题
例1:2019年9月,我们踏入了心仪的高中校园,找到了自己的班级.则下列对象中能构成一个集合的是哪些?并说明你的理由.
(1)你所在班级中的全体同学;
(2)班级中比较高的同学;
(3)班级中身高超过178 cm的同学;
(4)班级中比较胖的同学;
(5)班级中体重超过75 kg的同学;
(6)学习成绩比较好的同学
班级中的全体同学是确定的,所以可以构成一个集合
因为“比较高”无法衡量,所以对象不确定,所以不能构成一个集合
因为“身高超过178 cm”是确定的,所以可以构成一个集合
“比较胖”无法衡量,所以对象不确定,所以不能构成一个集合
“体重超过75 kg”是确定的,所以可以构成一个集合.
“学习成绩比较好”无法衡量,所以对象不确定,所以不能构成一个集合
3、常用数集及其记法
由数组成的集合叫数集
元素与集合
4、元素与集合的关系
.
元素a是集合A
的元素,
记作a A,
读作a属于A.
元素a不是集合A
的元素,
记作a A,
读作a不属于A.
典型例题
典例:用符号“ ”或“ ”填空:
(1)1___N, 0___N, -4___N, 0.3___N;
(2)1___Z, 0___Z, -4___Z, 0.3___Z;
(3)1___Q, 0___Q, -4___Q, 0.3___Q;
(4)1___R, 0___R, -4___R, 0.3___R.
典型例题
变式2: 用符号“ ”或“ ”填空:
(1)-3___N; (2) 3.14___ Q;
(3) ___Z; (4) - ___R;
(5) ___R; (6) 0 ___Z.
典型例题
×
√
√
×
√
√
(1)有限集:
含有有限个元素的集合
(2)无限集:
含有无限个元素的集合
不含任何元素的集合
叫做空集记作
6、集合的分类
5、集合的相等
例1:
(3)
练习
练习
追问2:当集合中元素个数有无数个,我们如何表示呢?
追问4:你能用描述法表示偶数集吗?
追问5:我们如何用描述法表示有理数集?
追问3:整数集Z可以分为奇数集和偶数集.我们如何用描述法表示奇数集?
练习
(5)Venn图(图示法)
(6)区间表示法(连续的数集)
课堂小结
这节课我们学习了元素和集合的含义,元素与集合的“属于”关系及用符号语言刻画集合.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
