数学人教A版(2019)选择性必修第三册6.1分类加法计数原理与分步乘法计数原理 课件(共37张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.1分类加法计数原理与分步乘法计数原理 课件(共37张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 08:51:41 | ||
图片预览










文档简介
(共37张PPT)
选择性必修三 第六章
计数原理
1.核糖核酸(RNA)分子有碱基按一定顺序排列而成。已知碱基有4种,但由成百上千个碱基组成的RNA分子的种数非常巨大。为什么?
2.若某地的汽车牌照由至多2个大写英文字母和3个阿拉伯数字构成,则共有多少个车牌号码可供民众挑选?
3.用红、黄、绿三面旗帜组成航海信号,颜色不同排列表示不同的信号,可组成多少种不同的信号?
6.1 分类加法计数原理
与
分步乘法计数原理
2023.03.22
问题1. 用1个大写英文字母或1个阿拉伯数字给教室座位编号,总共能编出多少种不同的号码?
课堂思考
问题2. 用1个大写英文字母和1个阿拉伯数字给教室座位编号(以A0,A1,
…,A9,B0,B1,…的方式)总共能编出多少种不同的号码?
编号有2类方案:
第一类方案:有26种不同方法;
第二类方案:有10种不同方法;
编号共有26+10=36种不同方法.
编号有2个步骤:
第一个步骤:有26种不同方法;
第二个步骤:有10种不同方法;
编号共有26×10=260种不同方法.
分类加法计数原理-P2
分步乘法计数原理-P4
问题1. 用1个大写英文字母或1个阿拉伯数字给教室座位编号,总共能编出多少种不同的号码?
★两个计数原理
问题2. 用1个大写英文字母和1个阿拉伯数字给教室座位编号(以A0,A1,…,B0,B1,…的方式)总共能编出多少种不同的号码?
编号共有26+10=36种不同方法.
编号共有26×10=260种不同方法.
分类加法计数原理-P2:
完成一件事有2类不同的方案,第1类方案有m种方法;
第2类方案有n种方法;
则完成该事共有m+n种方法.
分步乘法计数原理-P4:
完成一件事有2个步骤,
第1步有m种方法;
第2步有n种方法;
则完成该事共有m×n种方法.
无论第1步采用哪种方法,与之对应的第2步都有相同的方法数.
两类方案中的方法各不相同,用任何一种方法都可以完成这件事.
树状图
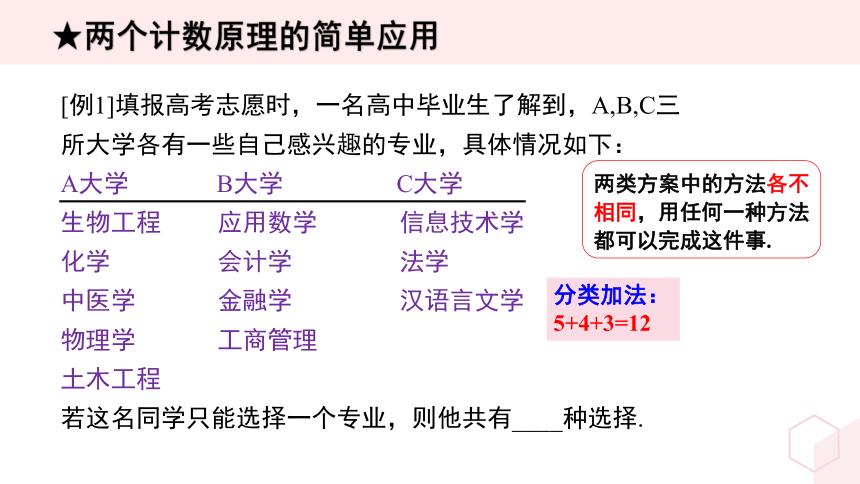
[例1]填报高考志愿时,一名高中毕业生了解到,A,B,C三所大学各有一些自己感兴趣的专业,具体情况如下:
A大学 B大学 C大学
生物工程 应用数学 信息技术学
化学 会计学 法学
中医学 金融学 汉语言文学
物理学 工商管理
土木工程
若这名同学只能选择一个专业,则他共有____种选择.
★两个计数原理的简单应用
分类加法:
5+4+3=12
两类方案中的方法各不相同,用任何一种方法都可以完成这件事.
[例2]某班有男生30名,女生24名,现要从中选出男、女生各一名,代表班级参加比赛,共有_______种不同的选法.
★两个计数原理的简单应用
析:第1步:选男生,有30种选法
第2步:选女生,有24种选法
共30×24=720种选法.
P7-2.从5名同学中选出正、副组长各1名,有多少种不同的选法?
析:先选正组长,再选副组长,共5×4=20种选法
P7-1.某电话局管辖范围内的电话号码由8位数字组成,其中前4位的数字是不变的,后4位数字都是0~9之间的一个数字,这个电话局不同的电话号码最多有多少个?
析:10×10×10×10=10000(个)
[例3]书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺
书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1、2、3层各取1本书,有多少种不同的取法?
(3)从书架上任取2种不同类型的书各1本,有多少种不同的取法?
注:有些较复杂的问题往往需要先“分类”,再在每一类中“分步”, 综合应用分类计数原理和分步计数原理.
★两个计数原理的简单应用
解: (1) 4+3+2=9.
(2) 4×3×2=24.
(3) 4×3+4×2+3×2=26.
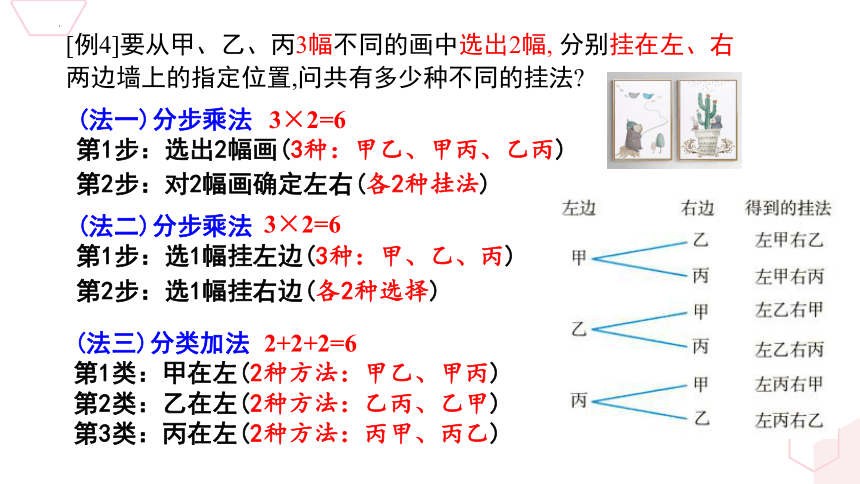
[例4]要从甲、乙、丙3幅不同的画中选出2幅, 分别挂在左、右
两边墙上的指定位置,问共有多少种不同的挂法
(法二)分步乘法
第1步:选1幅挂左边(3种:甲、乙、丙)
第2步:选1幅挂右边(各2种选择)
(法一)分步乘法
第1步:选出2幅画(3种:甲乙、甲丙、乙丙)
第2步:对2幅画确定左右(各2种挂法)
3×2=6
(法三)分类加法
第1类:甲在左(2种方法:甲乙、甲丙)
第2类:乙在左(2种方法:乙丙、乙甲)
第3类:丙在左(2种方法:丙甲、丙乙)
2+2+2=6
3×2=6
[例8]通常,我国民用汽车号牌的编号由两部分组成:第一部分为用汉字表示的、省、自治区、直辖市简称和用英文字母表示的发牌机关代号,第二部分为由阿拉伯数字和英文字母组成的序号,如图6.1-5所示.
其中,序号的编码规则为:
(1)由10个阿拉伯数字和除O,I之外的24个英文字母组成;
(2)最多只能有2个英文字母.
如果某地级市发牌机关采用5位序号编码,
那么这个发牌机关最多能发放多少张汽车号牌?
★两个计数原理的简单应用
析:①无字母:
10×10×10=1 000(种)
②1个字母:
(24×10×10×10)×5=1 200 000(种)
③2个字母:
(24×24×10×10×10)×10=5 760 000(种)
共1 000+1 200 000+5 760 000=7 060 000(种)
探究与发现:P12-13
——2种可能
——2种可能
——2种可能
分步乘法:2×2×…×2=2n.
n个2相乘
2n
P7-3.从1,2,…,19,20中任选一个数作被减数,再从1,2,…,10中
任选一个数作减数,然后写成一个减法算式,共可得到多少个不同的算式?
巩固:课本P7练习
析:20×10=200(个)
P7-4.在1,2,…,500中,被5除余2的数共有多少个?
P7-5.由数字1,2,3,4,5可以组成多少个三位数
①各位上的数字可以重复:
②各位上的数字不可以重复:
析:被5除余2的数为5n+2(n∈N),
5×5×5=125(种)
令1≤5n+2≤500,得0≤n≤99.
共100个
5×4×3=60(种)
巩固:课本P11-12练习
析:按个位数分类,共9+8+7+6+5+4+3+2+1=45(种)
2.在所有的两位数中,个位数字小于十位数字的有多少个?
3.某商场有6个门,如果某人从其中的任意一个门进入商场,并且要求从其他的门出去,那么共有多少种不同的进出商场的方式?
析:先选进入的门,再选出去的门,共6×5=30(种)
巩固:课本P11-12练习
4.任意画一条直线,在直线上任取n个分点.
(1)从这n个分点中任取2个点形成一条线段,可得到多少条线段?
(2)从这n个分点中任取2个点形成一个向量,可得到多少个向量?
2.如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路.从甲地到丁地共有多少条不同的路线?
析:共2×3+4×2=14(条)
巩固:课本P11-12练习
3.如图,要让电路从A处到B处接通,可有多少条不同的路径?
4.用1,5,9,13中的任意一个数作分子,4,8,12,16中任意一个数作分母,可构成多少个不同的分数?可构成多少个不同的真分数?
析:先定分子,再定分母,可构成4×4=15个不同的分数;
按分子分类,可构成4+3+2+1=10个不同的真分数;
巩固:课本P11-12练习
析:先定斜率,再定纵截距,共4×4=16条直线;
6.(1)在平面直角坐标系内,横坐标与纵坐标均在A={0,1,2,3,4,5}内取值的不同点共有多少个?
(2)在平面直角坐标系内,斜率在集合B={1,3,5,7}内取值,y轴上的截距在集合C={2,4,6,8}内取值的不同直线共有多少条?
析:先选横坐标,再选纵坐标,共6×6=36个不同的点.
7.一种号码锁有4个拨号盘,每个拨号盘上有0~9共10个数字.现最后一个拨号盘出现了故障,只能在0~5这6个数字中拨号,这4个拨号盘可组成多少个四位数字号码?
析:10×10×10×6=6000个四位数字号码
8.(1)4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每人限报其中的一个运动队,不同报法的种数是是34还是43?
[变式]4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每个运动队只选一名学生参加,不同的结果有____种.
析:人选运动队,每人有3种选择,共3×3×3×3=34=81
析:运动队选人,每队有4种选择,共4×4×4=43=64
巩固:课本P11-12练习
(2)3个班分别从5个景点中选择一处游览,不同选法的种数是35还是53?
析:各班选景点,每班有5种选择,共5×5×5=53=125
[变式]火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有_____种.
510
析:乘客选车站,每人有5种选择
[引例]从5件不同的礼物中选出2件,分别送给甲、乙两人,每人一件礼物,则不同的送法种数为_______.
9.(1)从5件不同的礼物中选出4件送给4位同学,每人一件,有多少种不同的送法?
(2)有5个编了号的抽屉,要放进3本不同的书,不同的放法有多少种?(一个抽屉可放多本书)
析:先选礼物给甲,再选礼物给乙,共5×4=20种选法
巩固:课本P11-12练习
析:依次选礼物给4位同学,共5×4×3×2=120种选法
析:①3本书放1个抽屉,
共5种放法;
②3本书放2个抽屉,
共3×(5×4)=60种放法;
③3本书放3个抽屉,
共5×4×3=60种放法;
共5+60+60=125种放法.
10.口袋中装有8个白球和10个红球,每个球编有不同的号码,现从中取出2个球.
(1)正好是白球、红球各一个的取法有多少种?
(2)正好是两个白球的取法有多少种?
(3)至少有一个白球的取法有多少种?
(4)两球的颜色相同的取法有多少种?
8×10=80
巩固:课本P11-12练习
(8×7)÷2=28
8×10+28=108
28+10×9÷2=73
3
4
4
3
11. 在国庆长假期间,要从7人中选若干人在7天假期值班(每天只需1人值班),不出现同一人连续值班2天,有多少种可能的安排方法?
12. 2160有多少个不同的正因数?
析:分步安排每天的值班人员,共7×6×6×6×6×6×6=7×65
巩固:课本P11-12练习
析:∵2160=24×5×33,
∴2160的正因数p=2a×5b×3c,
其中a可取0,1,2,3,4,b可取0,1,c可取0,1,2,3.
∴2160有5×2×4=40个不同的正因数.
题目点拨
1.“多面手”问题
[例1]7名学生中,3名会下象棋但不会下围棋,2名会下围棋但不会下象棋,2名既会下象棋又会下围棋,现从这7人中选出2人分别参加象棋比赛和围棋比赛,共有____种不同的选法.
3
象
2
围
2
多
(法1)
第1步:选出会象棋的,有5种选择;
第2步:选出会小号的,有4种选择;
共5×4=20种选法.
其中同个多面手2次均被选中的情况应排除,
(法2)
共3×2+2×2+3×2+2×1=18种选法.
排除法
分区法
故有20-2=18种选法
1.“多面手”问题
(法3)以“多面手”是否入选进行分类:
①“多面手”不入选:
综上,共6+10+2=18种选法.
先选多面手,再选另一名,共2×2+2×3=10种选法;
③“多面手”2名都入选:
有2种选法.
先选会象棋的,再选会围棋的,共3×2=6种选法;
②“多面手”只有1名入选:
[例1]7名学生中,3名会下象棋但不会下围棋,2名会下围棋但不会下象棋,2名既会下象棋又会下围棋,现从这7人中选出2人分别参加象棋比赛和围棋比赛,共有____种不同的选法.
3
象
2
围
2
多
1.“多面手”问题
[变式]某艺术小组有9人,每人至少会钢琴和小号中的1种乐器,其中8人会钢琴,5人会小号,从中选出会钢琴和会小号的各1人,有____种不同的选法.
先选出会钢琴的,有8种选择;
再选出会小号的,有5种选择;
共8×5=40种选法.
排除其中同个多面手2次均被选中的情况,
5钢
2小
3多
(排除法)
(分区法)
共5×3+3×2+5×2+3×2=37种选法.
多A 多A
多B 多B
多C 多C
故有40-3=37种选法
优先考虑特殊位置(首位不为0)
2.组数问题
[例2.1]用0,1,…,9这十个数字可组成多少个:
(1)三位数 (2)无重复数字的三位数
(3)有重复数字的三位数 (4)小于500的无重复数字的三位数
析:(1)依次确定百位、十位和个位数字的选法,
共9×10×10=900个三位数.
(2)依次确定百位、十位和个位数字的选法,
共9×9×8=648个无重复数字的三位数.
(4)依次确定百位、十位和个位数字的选法,
共4×9×8=288个.
(3)由(1)(2)得共900-648=252个有重复数字的三位数.
首(百)位不能取0
正难则反
百位取1,2,3,4
优先考虑特殊位置(个位的奇偶或首位不为0)
2.组数问题
(法1)①若个位为0,则依次确定百位、十位,共4×3=12种选法;
②若个位不为0,可取2,4,再依次确定百位、十位,
共2×3×3=18种选法;
[变式1]由0,1,2,3,4可组成多少个无重复数字的三位数的偶数
个位取偶数
百位不为0
综上,共12+18=30个无重复数字的三位数偶数.
(法2)依次确定个位、百位、十位,共3×4×3=36种选法;
排除百位为0的选法共2×3=6种,
综上,共36-6=30种选法
(法3)①个位为0,共4×3=12种选法;
②个位为2,共3×3=9种选法;
③个位为4,共3×3=9种选法;
综上,共12+9+9=30种选法
优先考虑特殊位置(个位的奇偶或首位不为0)
2.组数问题
[变式2]由0,1,2,3,4,5六个数字可组成多少个无重复数字的四位奇数
个位取奇数
千位不为0
析:依次确定个位、千位、百位、十位,
共3×4×4×3=144种选法;
[变式3]用0,1,2,3,4五个数字可组成多少个无重复数字且是3的倍数的三位数
故3个数字可以选0,1,2;0,2,4;1,2,3;2,3,4.
析:3的倍数的三位数,各个数位上的数字之和是3的倍数;
共4+4+6+6=20个.
[练习1]由0,1,2,3,4,5可组成_____个无重复数字且比2000大的四位偶数
120
个位取偶数
千位不取0,1
提示:按个位为0/2/4分三类,
依次确定千/百/十位
优先考虑特殊位置(个位的奇偶或首位不为0)
2.组数问题
[练习2]用0~5六个数字可组成____个无重复数字且比3042大的四位数.
①千位为4或5:千、百、十、个位各有2、5、4、3种选择;
②千位为3,百位不为0 :百、十、个位各有4、4、3种选择;
综上,符合的数共有2×5×4×3+4×4×3+1+3=172个
③千位为3,百位为0 :i)十位为4,个位为5
按千位进行分类:
3 _ _ _
3 0 _ _
4/5 _ _ _
ii)十位为5,个位为1/2/4
[练习3]用0~5六个数字可组成多少个无重复数字的且比40000大的五位偶数
(2×3-1)×4×3×2=120(个)
优先考虑特殊位置(个位的奇偶或首位不为0)
2.组数问题
[练习1]由0,1,2,3,4,5可组成多少个无重复数字且比2000大的四位偶数
①个位为0:共4×4×3=48种选法;
②个位为2:共3×4×3=36种选法;
共有48+36+36=120个
③个位为4:共3×4×3=36种选法;
(法1)按个位进行分类,依次确定千位、百位、十位,
_ _ _ 0
_ _ _ 2
_ _ _ 4
(法2)按千位分两类(2/4或3/5),依次确定千、个、百、十位,
共2×2×4×3+2×3×4×3=48+72=120种选法.
第2步:考虑百位,有4种选择;
共(3×4-2)×4×3=120(个)
第3步:考虑个位,有3种选择;
(法三)
第1步:考虑千位和个位:有3×4-2=12种选择;
个位取偶数
千位不取0,1
A
B
C
D
3.涂色/种植问题
[例3]如图,要给标有字母A、B、C、D等的区域涂色,
每格涂一色,同种颜色可用多次,但相邻区域涂不同色。
(1)若图①有5种颜色可选,则不同的涂色方案有___种;
共5×4×3×3=180种
5
3
4
3
5
3
4
3
C
B
A
D
图①
A B D
C 5
3
4
3
析:依次涂A,B,C,D,
依次涂B,C,A,D
[例3]如图,要给标有字母A、B、C、D等的区域涂色,
每格涂一色,同种颜色可用多次,但相邻区域须涂不同色。
(2)若图②有5种颜色可选,则不同的涂色方案有_____种;
3.涂色/种植问题
①B,D同色:共5×4×3×1×3=180种涂法
析:分步依次涂A,B,C,D,E,考虑B,D是否同色.
②B,D不同色:共5×4×3×2×2=240种涂法
A
B
C
D
E
5
4
3
?
A
B
C
D
E
图②
420
或分步依次涂C,B,A,D,E,考虑B,D是否同色.
3
3.涂色/种植问题小结
①按相对区域/顶点/面是否同色分类
②空间平面化→平面区域涂色
③按A,B,C,D…顺序或从有最多相邻的区域或点开始考虑.
各面涂色
条件同上
各点涂色
条件同上
各区涂色
条件同上
底
左
右
前
后
P
D
B
A
C
[练习1]如图,要给地图上标有字母A、B、C、D等的区域涂色,每格涂一色,同种颜色可使用多次,但相邻区域须涂不同色。
若图③有5种颜色可选,则不同的涂色方案有____种;
3.涂色/种植问题
析:D的涂法取决于A,C是否同色
①A,C同色:共5×4×1×4=80种涂法.
②A,C不同色:共5×4×3×3=120种涂法.
综上,共有80+120=200种.
分步依次涂A,B,C,D,考虑A,C是否同色
5
4
?
图③
A D
B C
或分步依次涂B,A,D,C,考虑B,D是否同色
题型四:涂色问题——点的涂色
[练习2]给图④的5个顶点涂色,同一条线段的两个端点不能同色,有4种颜色可选,则不同的涂色方法有___种.
4
3
2
2
(法1)分步依次涂E,A,B,C,D
E(4)→A(3)→B(2)→C(2)→D(2)
2
共4×3×2×2×2=96种
图④
(法2)分步依次涂A,B,C,D,E
A(4)→B(3)→C(与A同色 )→D(与B同色 )→E( )
分四类
注:从与其有最多相邻的区域或点开始考虑.
3.涂色/种植问题小结
[例4]将3种作物全部种植在如图所示的5块试验田中,每块种植一种作物,且相邻的试验田不能种同一种作物,则不同的种植方法共有________种.
析:依次种植5块田,使得相邻试验田种不同作物,
共3×2×2×2×2=48种种法.
其中只种2种作物的情况应排除,共3×2=6种,
故符合题意的种法共48-6=42种.
[变式]用1,2,3三个数字组成一个四位数,规定这三个数必须全部使用且同一数字不能相邻出现,这样的四位数有_____个.
3×2×2×2-6=18个
4.选取/分配问题
[例5]高三年级的三个班到甲、乙、丙、丁四个工厂进行社会实践,其中工厂甲必须有班级去,每班去何工厂可自由选择,则不同的分配方案有__________种.
(间接法)先计算3个班级自由选择去何工厂的总数,再排除
甲工厂无人去的情况,即有4×4×4-3×3×3=37种分配方案.
[变式]安排甲、乙、丙3名护士去6所医院实习,每所医院至多2人,则不同的分配方案共有________种.
(间接法)先计算3名护士自由选择去何医院的总数,再排除3人
到同一所医院的情况,即有6×6×6-6=210种分配方案.
END
选择性必修三 第六章
计数原理
1.核糖核酸(RNA)分子有碱基按一定顺序排列而成。已知碱基有4种,但由成百上千个碱基组成的RNA分子的种数非常巨大。为什么?
2.若某地的汽车牌照由至多2个大写英文字母和3个阿拉伯数字构成,则共有多少个车牌号码可供民众挑选?
3.用红、黄、绿三面旗帜组成航海信号,颜色不同排列表示不同的信号,可组成多少种不同的信号?
6.1 分类加法计数原理
与
分步乘法计数原理
2023.03.22
问题1. 用1个大写英文字母或1个阿拉伯数字给教室座位编号,总共能编出多少种不同的号码?
课堂思考
问题2. 用1个大写英文字母和1个阿拉伯数字给教室座位编号(以A0,A1,
…,A9,B0,B1,…的方式)总共能编出多少种不同的号码?
编号有2类方案:
第一类方案:有26种不同方法;
第二类方案:有10种不同方法;
编号共有26+10=36种不同方法.
编号有2个步骤:
第一个步骤:有26种不同方法;
第二个步骤:有10种不同方法;
编号共有26×10=260种不同方法.
分类加法计数原理-P2
分步乘法计数原理-P4
问题1. 用1个大写英文字母或1个阿拉伯数字给教室座位编号,总共能编出多少种不同的号码?
★两个计数原理
问题2. 用1个大写英文字母和1个阿拉伯数字给教室座位编号(以A0,A1,…,B0,B1,…的方式)总共能编出多少种不同的号码?
编号共有26+10=36种不同方法.
编号共有26×10=260种不同方法.
分类加法计数原理-P2:
完成一件事有2类不同的方案,第1类方案有m种方法;
第2类方案有n种方法;
则完成该事共有m+n种方法.
分步乘法计数原理-P4:
完成一件事有2个步骤,
第1步有m种方法;
第2步有n种方法;
则完成该事共有m×n种方法.
无论第1步采用哪种方法,与之对应的第2步都有相同的方法数.
两类方案中的方法各不相同,用任何一种方法都可以完成这件事.
树状图
[例1]填报高考志愿时,一名高中毕业生了解到,A,B,C三所大学各有一些自己感兴趣的专业,具体情况如下:
A大学 B大学 C大学
生物工程 应用数学 信息技术学
化学 会计学 法学
中医学 金融学 汉语言文学
物理学 工商管理
土木工程
若这名同学只能选择一个专业,则他共有____种选择.
★两个计数原理的简单应用
分类加法:
5+4+3=12
两类方案中的方法各不相同,用任何一种方法都可以完成这件事.
[例2]某班有男生30名,女生24名,现要从中选出男、女生各一名,代表班级参加比赛,共有_______种不同的选法.
★两个计数原理的简单应用
析:第1步:选男生,有30种选法
第2步:选女生,有24种选法
共30×24=720种选法.
P7-2.从5名同学中选出正、副组长各1名,有多少种不同的选法?
析:先选正组长,再选副组长,共5×4=20种选法
P7-1.某电话局管辖范围内的电话号码由8位数字组成,其中前4位的数字是不变的,后4位数字都是0~9之间的一个数字,这个电话局不同的电话号码最多有多少个?
析:10×10×10×10=10000(个)
[例3]书架的第1层放有4本不同的计算机书,第2层放有3本不同的文艺
书,第3层放有2本不同的体育书.
(1)从书架上任取1本书,有多少种不同的取法?
(2)从书架的第1、2、3层各取1本书,有多少种不同的取法?
(3)从书架上任取2种不同类型的书各1本,有多少种不同的取法?
注:有些较复杂的问题往往需要先“分类”,再在每一类中“分步”, 综合应用分类计数原理和分步计数原理.
★两个计数原理的简单应用
解: (1) 4+3+2=9.
(2) 4×3×2=24.
(3) 4×3+4×2+3×2=26.
[例4]要从甲、乙、丙3幅不同的画中选出2幅, 分别挂在左、右
两边墙上的指定位置,问共有多少种不同的挂法
(法二)分步乘法
第1步:选1幅挂左边(3种:甲、乙、丙)
第2步:选1幅挂右边(各2种选择)
(法一)分步乘法
第1步:选出2幅画(3种:甲乙、甲丙、乙丙)
第2步:对2幅画确定左右(各2种挂法)
3×2=6
(法三)分类加法
第1类:甲在左(2种方法:甲乙、甲丙)
第2类:乙在左(2种方法:乙丙、乙甲)
第3类:丙在左(2种方法:丙甲、丙乙)
2+2+2=6
3×2=6
[例8]通常,我国民用汽车号牌的编号由两部分组成:第一部分为用汉字表示的、省、自治区、直辖市简称和用英文字母表示的发牌机关代号,第二部分为由阿拉伯数字和英文字母组成的序号,如图6.1-5所示.
其中,序号的编码规则为:
(1)由10个阿拉伯数字和除O,I之外的24个英文字母组成;
(2)最多只能有2个英文字母.
如果某地级市发牌机关采用5位序号编码,
那么这个发牌机关最多能发放多少张汽车号牌?
★两个计数原理的简单应用
析:①无字母:
10×10×10=1 000(种)
②1个字母:
(24×10×10×10)×5=1 200 000(种)
③2个字母:
(24×24×10×10×10)×10=5 760 000(种)
共1 000+1 200 000+5 760 000=7 060 000(种)
探究与发现:P12-13
——2种可能
——2种可能
——2种可能
分步乘法:2×2×…×2=2n.
n个2相乘
2n
P7-3.从1,2,…,19,20中任选一个数作被减数,再从1,2,…,10中
任选一个数作减数,然后写成一个减法算式,共可得到多少个不同的算式?
巩固:课本P7练习
析:20×10=200(个)
P7-4.在1,2,…,500中,被5除余2的数共有多少个?
P7-5.由数字1,2,3,4,5可以组成多少个三位数
①各位上的数字可以重复:
②各位上的数字不可以重复:
析:被5除余2的数为5n+2(n∈N),
5×5×5=125(种)
令1≤5n+2≤500,得0≤n≤99.
共100个
5×4×3=60(种)
巩固:课本P11-12练习
析:按个位数分类,共9+8+7+6+5+4+3+2+1=45(种)
2.在所有的两位数中,个位数字小于十位数字的有多少个?
3.某商场有6个门,如果某人从其中的任意一个门进入商场,并且要求从其他的门出去,那么共有多少种不同的进出商场的方式?
析:先选进入的门,再选出去的门,共6×5=30(种)
巩固:课本P11-12练习
4.任意画一条直线,在直线上任取n个分点.
(1)从这n个分点中任取2个点形成一条线段,可得到多少条线段?
(2)从这n个分点中任取2个点形成一个向量,可得到多少个向量?
2.如图,从甲地到乙地有2条路,从乙地到丁地有3条路;从甲地到丙地有4条路,从丙地到丁地有2条路.从甲地到丁地共有多少条不同的路线?
析:共2×3+4×2=14(条)
巩固:课本P11-12练习
3.如图,要让电路从A处到B处接通,可有多少条不同的路径?
4.用1,5,9,13中的任意一个数作分子,4,8,12,16中任意一个数作分母,可构成多少个不同的分数?可构成多少个不同的真分数?
析:先定分子,再定分母,可构成4×4=15个不同的分数;
按分子分类,可构成4+3+2+1=10个不同的真分数;
巩固:课本P11-12练习
析:先定斜率,再定纵截距,共4×4=16条直线;
6.(1)在平面直角坐标系内,横坐标与纵坐标均在A={0,1,2,3,4,5}内取值的不同点共有多少个?
(2)在平面直角坐标系内,斜率在集合B={1,3,5,7}内取值,y轴上的截距在集合C={2,4,6,8}内取值的不同直线共有多少条?
析:先选横坐标,再选纵坐标,共6×6=36个不同的点.
7.一种号码锁有4个拨号盘,每个拨号盘上有0~9共10个数字.现最后一个拨号盘出现了故障,只能在0~5这6个数字中拨号,这4个拨号盘可组成多少个四位数字号码?
析:10×10×10×6=6000个四位数字号码
8.(1)4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每人限报其中的一个运动队,不同报法的种数是是34还是43?
[变式]4名同学分别报名参加学校的足球队、篮球队、乒乓球队,每个运动队只选一名学生参加,不同的结果有____种.
析:人选运动队,每人有3种选择,共3×3×3×3=34=81
析:运动队选人,每队有4种选择,共4×4×4=43=64
巩固:课本P11-12练习
(2)3个班分别从5个景点中选择一处游览,不同选法的种数是35还是53?
析:各班选景点,每班有5种选择,共5×5×5=53=125
[变式]火车上有10名乘客,沿途有5个车站,乘客下车的可能方式有_____种.
510
析:乘客选车站,每人有5种选择
[引例]从5件不同的礼物中选出2件,分别送给甲、乙两人,每人一件礼物,则不同的送法种数为_______.
9.(1)从5件不同的礼物中选出4件送给4位同学,每人一件,有多少种不同的送法?
(2)有5个编了号的抽屉,要放进3本不同的书,不同的放法有多少种?(一个抽屉可放多本书)
析:先选礼物给甲,再选礼物给乙,共5×4=20种选法
巩固:课本P11-12练习
析:依次选礼物给4位同学,共5×4×3×2=120种选法
析:①3本书放1个抽屉,
共5种放法;
②3本书放2个抽屉,
共3×(5×4)=60种放法;
③3本书放3个抽屉,
共5×4×3=60种放法;
共5+60+60=125种放法.
10.口袋中装有8个白球和10个红球,每个球编有不同的号码,现从中取出2个球.
(1)正好是白球、红球各一个的取法有多少种?
(2)正好是两个白球的取法有多少种?
(3)至少有一个白球的取法有多少种?
(4)两球的颜色相同的取法有多少种?
8×10=80
巩固:课本P11-12练习
(8×7)÷2=28
8×10+28=108
28+10×9÷2=73
3
4
4
3
11. 在国庆长假期间,要从7人中选若干人在7天假期值班(每天只需1人值班),不出现同一人连续值班2天,有多少种可能的安排方法?
12. 2160有多少个不同的正因数?
析:分步安排每天的值班人员,共7×6×6×6×6×6×6=7×65
巩固:课本P11-12练习
析:∵2160=24×5×33,
∴2160的正因数p=2a×5b×3c,
其中a可取0,1,2,3,4,b可取0,1,c可取0,1,2,3.
∴2160有5×2×4=40个不同的正因数.
题目点拨
1.“多面手”问题
[例1]7名学生中,3名会下象棋但不会下围棋,2名会下围棋但不会下象棋,2名既会下象棋又会下围棋,现从这7人中选出2人分别参加象棋比赛和围棋比赛,共有____种不同的选法.
3
象
2
围
2
多
(法1)
第1步:选出会象棋的,有5种选择;
第2步:选出会小号的,有4种选择;
共5×4=20种选法.
其中同个多面手2次均被选中的情况应排除,
(法2)
共3×2+2×2+3×2+2×1=18种选法.
排除法
分区法
故有20-2=18种选法
1.“多面手”问题
(法3)以“多面手”是否入选进行分类:
①“多面手”不入选:
综上,共6+10+2=18种选法.
先选多面手,再选另一名,共2×2+2×3=10种选法;
③“多面手”2名都入选:
有2种选法.
先选会象棋的,再选会围棋的,共3×2=6种选法;
②“多面手”只有1名入选:
[例1]7名学生中,3名会下象棋但不会下围棋,2名会下围棋但不会下象棋,2名既会下象棋又会下围棋,现从这7人中选出2人分别参加象棋比赛和围棋比赛,共有____种不同的选法.
3
象
2
围
2
多
1.“多面手”问题
[变式]某艺术小组有9人,每人至少会钢琴和小号中的1种乐器,其中8人会钢琴,5人会小号,从中选出会钢琴和会小号的各1人,有____种不同的选法.
先选出会钢琴的,有8种选择;
再选出会小号的,有5种选择;
共8×5=40种选法.
排除其中同个多面手2次均被选中的情况,
5钢
2小
3多
(排除法)
(分区法)
共5×3+3×2+5×2+3×2=37种选法.
多A 多A
多B 多B
多C 多C
故有40-3=37种选法
优先考虑特殊位置(首位不为0)
2.组数问题
[例2.1]用0,1,…,9这十个数字可组成多少个:
(1)三位数 (2)无重复数字的三位数
(3)有重复数字的三位数 (4)小于500的无重复数字的三位数
析:(1)依次确定百位、十位和个位数字的选法,
共9×10×10=900个三位数.
(2)依次确定百位、十位和个位数字的选法,
共9×9×8=648个无重复数字的三位数.
(4)依次确定百位、十位和个位数字的选法,
共4×9×8=288个.
(3)由(1)(2)得共900-648=252个有重复数字的三位数.
首(百)位不能取0
正难则反
百位取1,2,3,4
优先考虑特殊位置(个位的奇偶或首位不为0)
2.组数问题
(法1)①若个位为0,则依次确定百位、十位,共4×3=12种选法;
②若个位不为0,可取2,4,再依次确定百位、十位,
共2×3×3=18种选法;
[变式1]由0,1,2,3,4可组成多少个无重复数字的三位数的偶数
个位取偶数
百位不为0
综上,共12+18=30个无重复数字的三位数偶数.
(法2)依次确定个位、百位、十位,共3×4×3=36种选法;
排除百位为0的选法共2×3=6种,
综上,共36-6=30种选法
(法3)①个位为0,共4×3=12种选法;
②个位为2,共3×3=9种选法;
③个位为4,共3×3=9种选法;
综上,共12+9+9=30种选法
优先考虑特殊位置(个位的奇偶或首位不为0)
2.组数问题
[变式2]由0,1,2,3,4,5六个数字可组成多少个无重复数字的四位奇数
个位取奇数
千位不为0
析:依次确定个位、千位、百位、十位,
共3×4×4×3=144种选法;
[变式3]用0,1,2,3,4五个数字可组成多少个无重复数字且是3的倍数的三位数
故3个数字可以选0,1,2;0,2,4;1,2,3;2,3,4.
析:3的倍数的三位数,各个数位上的数字之和是3的倍数;
共4+4+6+6=20个.
[练习1]由0,1,2,3,4,5可组成_____个无重复数字且比2000大的四位偶数
120
个位取偶数
千位不取0,1
提示:按个位为0/2/4分三类,
依次确定千/百/十位
优先考虑特殊位置(个位的奇偶或首位不为0)
2.组数问题
[练习2]用0~5六个数字可组成____个无重复数字且比3042大的四位数.
①千位为4或5:千、百、十、个位各有2、5、4、3种选择;
②千位为3,百位不为0 :百、十、个位各有4、4、3种选择;
综上,符合的数共有2×5×4×3+4×4×3+1+3=172个
③千位为3,百位为0 :i)十位为4,个位为5
按千位进行分类:
3 _ _ _
3 0 _ _
4/5 _ _ _
ii)十位为5,个位为1/2/4
[练习3]用0~5六个数字可组成多少个无重复数字的且比40000大的五位偶数
(2×3-1)×4×3×2=120(个)
优先考虑特殊位置(个位的奇偶或首位不为0)
2.组数问题
[练习1]由0,1,2,3,4,5可组成多少个无重复数字且比2000大的四位偶数
①个位为0:共4×4×3=48种选法;
②个位为2:共3×4×3=36种选法;
共有48+36+36=120个
③个位为4:共3×4×3=36种选法;
(法1)按个位进行分类,依次确定千位、百位、十位,
_ _ _ 0
_ _ _ 2
_ _ _ 4
(法2)按千位分两类(2/4或3/5),依次确定千、个、百、十位,
共2×2×4×3+2×3×4×3=48+72=120种选法.
第2步:考虑百位,有4种选择;
共(3×4-2)×4×3=120(个)
第3步:考虑个位,有3种选择;
(法三)
第1步:考虑千位和个位:有3×4-2=12种选择;
个位取偶数
千位不取0,1
A
B
C
D
3.涂色/种植问题
[例3]如图,要给标有字母A、B、C、D等的区域涂色,
每格涂一色,同种颜色可用多次,但相邻区域涂不同色。
(1)若图①有5种颜色可选,则不同的涂色方案有___种;
共5×4×3×3=180种
5
3
4
3
5
3
4
3
C
B
A
D
图①
A B D
C 5
3
4
3
析:依次涂A,B,C,D,
依次涂B,C,A,D
[例3]如图,要给标有字母A、B、C、D等的区域涂色,
每格涂一色,同种颜色可用多次,但相邻区域须涂不同色。
(2)若图②有5种颜色可选,则不同的涂色方案有_____种;
3.涂色/种植问题
①B,D同色:共5×4×3×1×3=180种涂法
析:分步依次涂A,B,C,D,E,考虑B,D是否同色.
②B,D不同色:共5×4×3×2×2=240种涂法
A
B
C
D
E
5
4
3
?
A
B
C
D
E
图②
420
或分步依次涂C,B,A,D,E,考虑B,D是否同色.
3
3.涂色/种植问题小结
①按相对区域/顶点/面是否同色分类
②空间平面化→平面区域涂色
③按A,B,C,D…顺序或从有最多相邻的区域或点开始考虑.
各面涂色
条件同上
各点涂色
条件同上
各区涂色
条件同上
底
左
右
前
后
P
D
B
A
C
[练习1]如图,要给地图上标有字母A、B、C、D等的区域涂色,每格涂一色,同种颜色可使用多次,但相邻区域须涂不同色。
若图③有5种颜色可选,则不同的涂色方案有____种;
3.涂色/种植问题
析:D的涂法取决于A,C是否同色
①A,C同色:共5×4×1×4=80种涂法.
②A,C不同色:共5×4×3×3=120种涂法.
综上,共有80+120=200种.
分步依次涂A,B,C,D,考虑A,C是否同色
5
4
?
图③
A D
B C
或分步依次涂B,A,D,C,考虑B,D是否同色
题型四:涂色问题——点的涂色
[练习2]给图④的5个顶点涂色,同一条线段的两个端点不能同色,有4种颜色可选,则不同的涂色方法有___种.
4
3
2
2
(法1)分步依次涂E,A,B,C,D
E(4)→A(3)→B(2)→C(2)→D(2)
2
共4×3×2×2×2=96种
图④
(法2)分步依次涂A,B,C,D,E
A(4)→B(3)→C(与A同色 )→D(与B同色 )→E( )
分四类
注:从与其有最多相邻的区域或点开始考虑.
3.涂色/种植问题小结
[例4]将3种作物全部种植在如图所示的5块试验田中,每块种植一种作物,且相邻的试验田不能种同一种作物,则不同的种植方法共有________种.
析:依次种植5块田,使得相邻试验田种不同作物,
共3×2×2×2×2=48种种法.
其中只种2种作物的情况应排除,共3×2=6种,
故符合题意的种法共48-6=42种.
[变式]用1,2,3三个数字组成一个四位数,规定这三个数必须全部使用且同一数字不能相邻出现,这样的四位数有_____个.
3×2×2×2-6=18个
4.选取/分配问题
[例5]高三年级的三个班到甲、乙、丙、丁四个工厂进行社会实践,其中工厂甲必须有班级去,每班去何工厂可自由选择,则不同的分配方案有__________种.
(间接法)先计算3个班级自由选择去何工厂的总数,再排除
甲工厂无人去的情况,即有4×4×4-3×3×3=37种分配方案.
[变式]安排甲、乙、丙3名护士去6所医院实习,每所医院至多2人,则不同的分配方案共有________种.
(间接法)先计算3名护士自由选择去何医院的总数,再排除3人
到同一所医院的情况,即有6×6×6-6=210种分配方案.
END
