数学人教A版(2019)选择性必修第三册6.3二项式定理 课件(共45张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.3二项式定理 课件(共45张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 00:00:00 | ||
图片预览











文档简介
(共45张PPT)
6.3 二项式定理
Q1:下面各式如何展开 展开且合并同类项后的各项及系数/次数是什么
(a+b)2
(a+b)3
=a3+3a2b+3ab2+b3
= a2+2ab+b2
(a+b)4
=(a+b)(a+b)
=(a+b)(a+b)(a+b)
=(a+b)(a+b)(a+b)(a+b)
展开方式:从每个(a+b)中选一个数a或b,相乘后得到一项
=a4+__a3b+__a2b2+__ab3+b4
4
6
4
选0个b
选1个b
选2个b
选0个b
选1个b
选2个b
选3个b
Q2:你能否根据上述规律,写出(a+b)n的展开式中的各项及其系数?
(a+b)n
=(a+b)(a+b)···(a+b)(a+b)
=___an
+__an-1b
+__an-2b2
+__an-3b3
+···
+___abn-1
+__bn
n个
展开方式:依次从每个(a+b)中选一个数a或b,相乘后得到一项
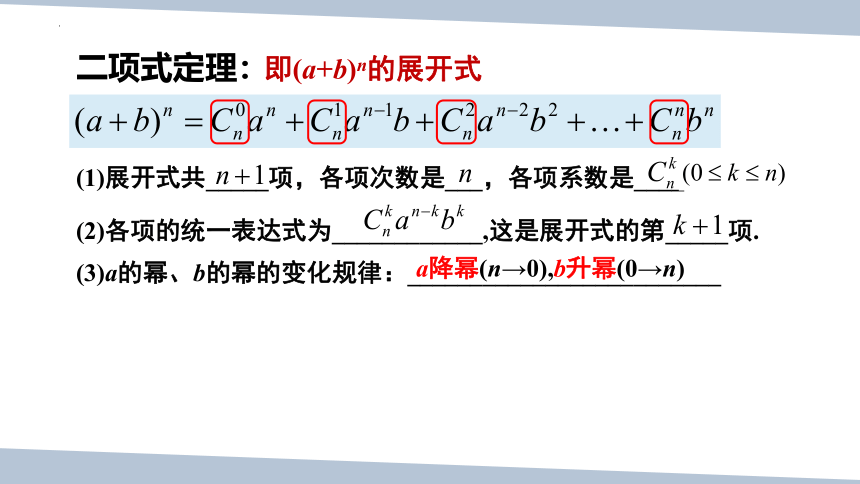
二项式定理:
即(a+b)n的展开式
(1)展开式共_____项,各项次数是___,各项系数是____.
(2)各项的统一表达式为____________,这是展开式的第_____项.
(3)a的幂、b的幂的变化规律:_________________________
a降幂(n→0),b升幂(0→n)
二项式定理:
即(a+b)n的展开式
(1)展开式共n+1项,各项次数为n.
(2)各项规律:a降幂(n→0);b升幂(0→n)
(3)展开式的通项or第k+1项:
(4)各项的二项式系数:(k=0,1,2,…,n)
二项式定理:
即(a+b)n的展开式
(4)各项的二项式系数:(k=0,1,2,…,n)
(a+b)3=a3+3a2b+3ab2+b3
(a+b)2=a2+2ab+b2
(a+b)4=a4+4a3b+10a2b2+4ab3+b4
基础巩固:求二项式的展开式
先写通项,再将0,1,2,…n代入k
基础巩固:求二项式的展开式
先写通项,再将0,1,2,…n代入k
括号内先化简,再展开
基础巩固:二项式定理
a降幂(n→0),b升幂(0→n)
a=1,b=3
a=2,b=-1
a=x-1,b=1
3n
1
x5-1
新知:二项式系数的性质
只与n有关,与a,b无关.
基础巩固:二项式系数的性质
3.一串装饰彩灯由灯泡串联而成,每串有20个灯泡,只要有一个灯泡坏了,整串灯泡就不亮,则因灯泡损坏致使一串彩灯不亮的可能性的种数为( )
A.20 B.219 C.220 D.220-1
D
例题点拨:求二项式的指定项或其系数
例题点拨:求二项式的指定项或其系数
﹣56
56
例题点拨:求二项式的指定项或其系数
有理项:所有的字母的指数恰好都是整数的项
例题点拨:求二项式的指定项或其系数
综合运用:求二项式的指定项或其系数
推广运用:求多项式的指定项或其系数
推广运用:求多项式的指定项或其系数
推广运用:求多项式的指定项或其系数
选2个y
选1个x2
选2个x
推广运用:求多项式的指定项或其系数
240
240
6.3.2二项式系数的性质
(二项式)系数和与系数的最值
二项式系数的性质
(a+b)3=a3+3a2b+3ab2+b3
(a+b)2=a2+2ab+b2
(a+b)4=a4+4a3b+10a2b2+4ab3+b4
n (a+b)n展开式的二项式系数 (a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
1
6
15
20
15
6
1
1
5
10
10
5
1
1
4
6
4
1
1
3
3
1
1
2
1
1
1
观察与发现:杨辉三角(二项式系数表)
①每行的两端都是1.
②递推性:除1以外的每一个数都等于它肩上两数的和.
③对称性:与首末两端等距的两个二项式系数相等.
④增减性:先增后减,在中间项取得最大值.
二项式系数的增减性与最值
二项式系数先增后减,关于k=对称.
二项式系数在中间项取得最大值.
第8项为中间项
共15项
14
8
4和5
11
6
例题点拨(2):各项系数的问题
例题点拨(2):各项系数的问题
赋值法:可解决系数和问题
X
Y
例题点拨(2):各项系数的问题
(法1:系数单调性→系数最大值)
例题点拨(2):各项系数的问题
(法2:系数极大值→系数最大值)
例题点拨(2):各项系数的问题
系数最大:正系数中的最大
系数最小:负系数中的最小
系数绝对值最大
共性
小结:系数的求和与最值问题
1.二项式系数和:
2.奇/偶数项的二项式系数和:
3.各项系数和X+Y:
4.奇数项的系数和X:
5.系数ak(ak为正)的最大值:
6.系数|ak|(ak正负交替)的最大值:
7.系数ak(ak正负交替)的最大/小值:
8.系数a0:
展开式的系数和
展开式的系数和——赋值法
展开式的系数和——赋值法
5
展开式的系数和——赋值法
拓展:整除与余数问题
二项式定理的应用——整除和余数问题
二项式定理的应用——整除和余数问题
二项式定理的应用——整除和余数问题
结合除数,将底数化成两数的和或差的形式
二项式定理的应用——整除和余数问题
被11整除
被11整除
8
二项式定理的应用——整除和余数问题
7
被9整除
余数的取值范围为0到除数之间(不包括除数)的整数
被9除的余数是﹣2
被9除的余数是7
FIGHTING
6.3 二项式定理
Q1:下面各式如何展开 展开且合并同类项后的各项及系数/次数是什么
(a+b)2
(a+b)3
=a3+3a2b+3ab2+b3
= a2+2ab+b2
(a+b)4
=(a+b)(a+b)
=(a+b)(a+b)(a+b)
=(a+b)(a+b)(a+b)(a+b)
展开方式:从每个(a+b)中选一个数a或b,相乘后得到一项
=a4+__a3b+__a2b2+__ab3+b4
4
6
4
选0个b
选1个b
选2个b
选0个b
选1个b
选2个b
选3个b
Q2:你能否根据上述规律,写出(a+b)n的展开式中的各项及其系数?
(a+b)n
=(a+b)(a+b)···(a+b)(a+b)
=___an
+__an-1b
+__an-2b2
+__an-3b3
+···
+___abn-1
+__bn
n个
展开方式:依次从每个(a+b)中选一个数a或b,相乘后得到一项
二项式定理:
即(a+b)n的展开式
(1)展开式共_____项,各项次数是___,各项系数是____.
(2)各项的统一表达式为____________,这是展开式的第_____项.
(3)a的幂、b的幂的变化规律:_________________________
a降幂(n→0),b升幂(0→n)
二项式定理:
即(a+b)n的展开式
(1)展开式共n+1项,各项次数为n.
(2)各项规律:a降幂(n→0);b升幂(0→n)
(3)展开式的通项or第k+1项:
(4)各项的二项式系数:(k=0,1,2,…,n)
二项式定理:
即(a+b)n的展开式
(4)各项的二项式系数:(k=0,1,2,…,n)
(a+b)3=a3+3a2b+3ab2+b3
(a+b)2=a2+2ab+b2
(a+b)4=a4+4a3b+10a2b2+4ab3+b4
基础巩固:求二项式的展开式
先写通项,再将0,1,2,…n代入k
基础巩固:求二项式的展开式
先写通项,再将0,1,2,…n代入k
括号内先化简,再展开
基础巩固:二项式定理
a降幂(n→0),b升幂(0→n)
a=1,b=3
a=2,b=-1
a=x-1,b=1
3n
1
x5-1
新知:二项式系数的性质
只与n有关,与a,b无关.
基础巩固:二项式系数的性质
3.一串装饰彩灯由灯泡串联而成,每串有20个灯泡,只要有一个灯泡坏了,整串灯泡就不亮,则因灯泡损坏致使一串彩灯不亮的可能性的种数为( )
A.20 B.219 C.220 D.220-1
D
例题点拨:求二项式的指定项或其系数
例题点拨:求二项式的指定项或其系数
﹣56
56
例题点拨:求二项式的指定项或其系数
有理项:所有的字母的指数恰好都是整数的项
例题点拨:求二项式的指定项或其系数
综合运用:求二项式的指定项或其系数
推广运用:求多项式的指定项或其系数
推广运用:求多项式的指定项或其系数
推广运用:求多项式的指定项或其系数
选2个y
选1个x2
选2个x
推广运用:求多项式的指定项或其系数
240
240
6.3.2二项式系数的性质
(二项式)系数和与系数的最值
二项式系数的性质
(a+b)3=a3+3a2b+3ab2+b3
(a+b)2=a2+2ab+b2
(a+b)4=a4+4a3b+10a2b2+4ab3+b4
n (a+b)n展开式的二项式系数 (a+b)1
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
1
6
15
20
15
6
1
1
5
10
10
5
1
1
4
6
4
1
1
3
3
1
1
2
1
1
1
观察与发现:杨辉三角(二项式系数表)
①每行的两端都是1.
②递推性:除1以外的每一个数都等于它肩上两数的和.
③对称性:与首末两端等距的两个二项式系数相等.
④增减性:先增后减,在中间项取得最大值.
二项式系数的增减性与最值
二项式系数先增后减,关于k=对称.
二项式系数在中间项取得最大值.
第8项为中间项
共15项
14
8
4和5
11
6
例题点拨(2):各项系数的问题
例题点拨(2):各项系数的问题
赋值法:可解决系数和问题
X
Y
例题点拨(2):各项系数的问题
(法1:系数单调性→系数最大值)
例题点拨(2):各项系数的问题
(法2:系数极大值→系数最大值)
例题点拨(2):各项系数的问题
系数最大:正系数中的最大
系数最小:负系数中的最小
系数绝对值最大
共性
小结:系数的求和与最值问题
1.二项式系数和:
2.奇/偶数项的二项式系数和:
3.各项系数和X+Y:
4.奇数项的系数和X:
5.系数ak(ak为正)的最大值:
6.系数|ak|(ak正负交替)的最大值:
7.系数ak(ak正负交替)的最大/小值:
8.系数a0:
展开式的系数和
展开式的系数和——赋值法
展开式的系数和——赋值法
5
展开式的系数和——赋值法
拓展:整除与余数问题
二项式定理的应用——整除和余数问题
二项式定理的应用——整除和余数问题
二项式定理的应用——整除和余数问题
结合除数,将底数化成两数的和或差的形式
二项式定理的应用——整除和余数问题
被11整除
被11整除
8
二项式定理的应用——整除和余数问题
7
被9整除
余数的取值范围为0到除数之间(不包括除数)的整数
被9除的余数是﹣2
被9除的余数是7
FIGHTING
