数学人教A版(2019)必修第一册5.1.1任意角 课件(共44张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.1任意角 课件(共44张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-05 08:52:49 | ||
图片预览





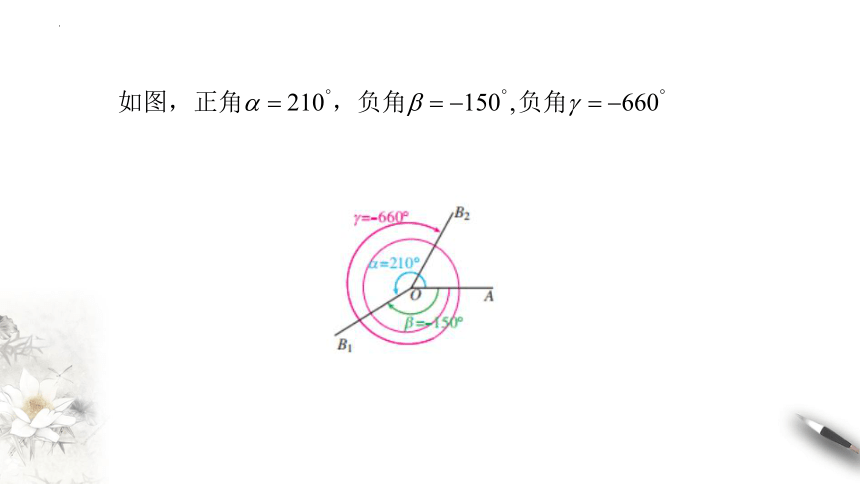


文档简介
(共44张PPT)
人教2019版必修第一册
第五章 三角函数
5.1.1 任意角
课程目标
1.了解任意角的概念.
2.理解象限角的概念及终边相同的角的含义.
3.掌握判断象限角及表示终边相同的角的方法.
数学学科素养
1.数学抽象:理解任意角的概念,能区分各类角;
2.逻辑推理:求区间角;
3.数学运算:会判断象限角及终边相同的角.
自主预习,回答问题
阅读课本168-170页,思考并完成以下问题
1.角是如何推广的 角的概念推广后,分类的标准是什么?
2.如何判断角所在的象限?
3.终边相同的角一定相等吗?如何表示终边相同的角?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
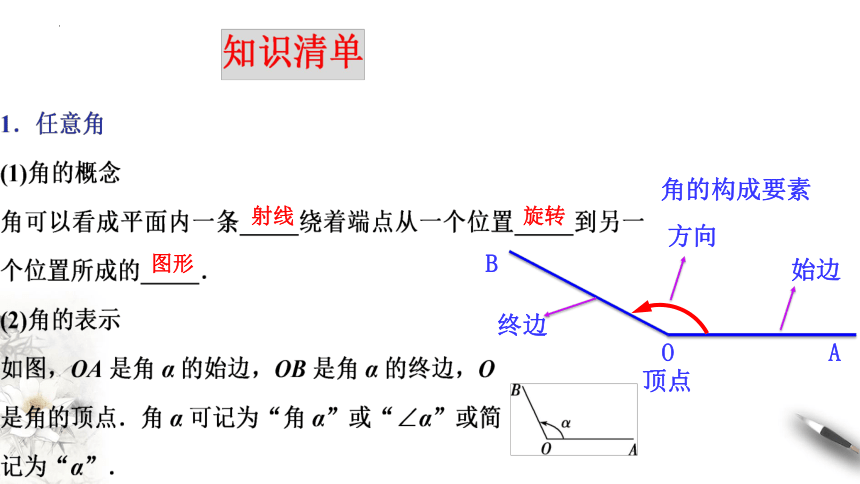
射线
旋转
图形
角的构成要素
始边
终边
顶点
A
B
O
方向
逆时针
顺时针
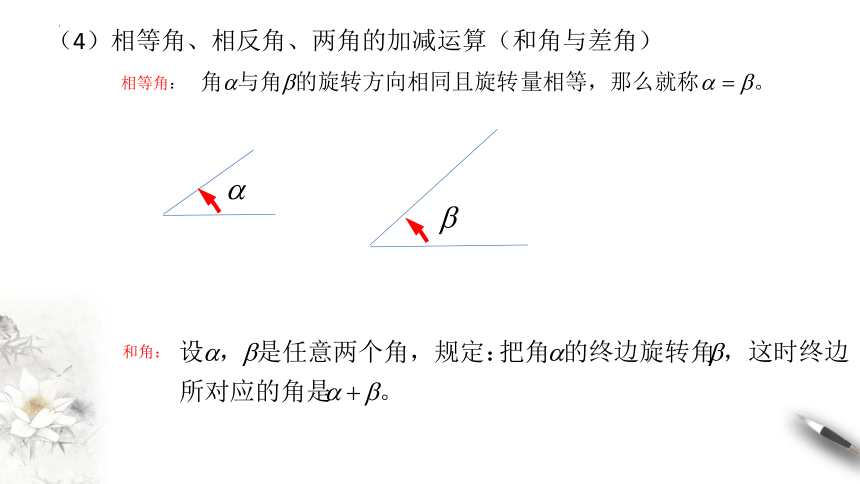
(4)相等角、相反角、两角的加减运算(和角与差角)
相等角:
和角:
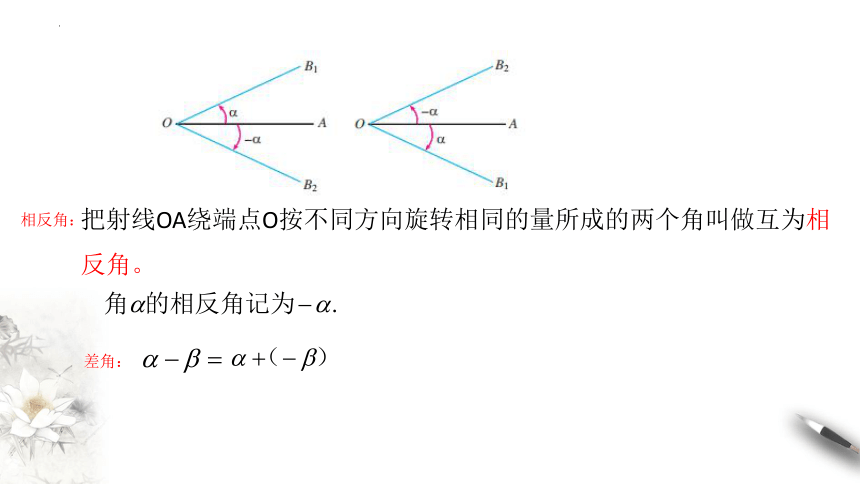
把射线OA绕端点O按不同方向旋转相同的量所成的两个角叫做互为相
反角。
相反角:
差角:
原点
x
终边
象限角
坐标轴上
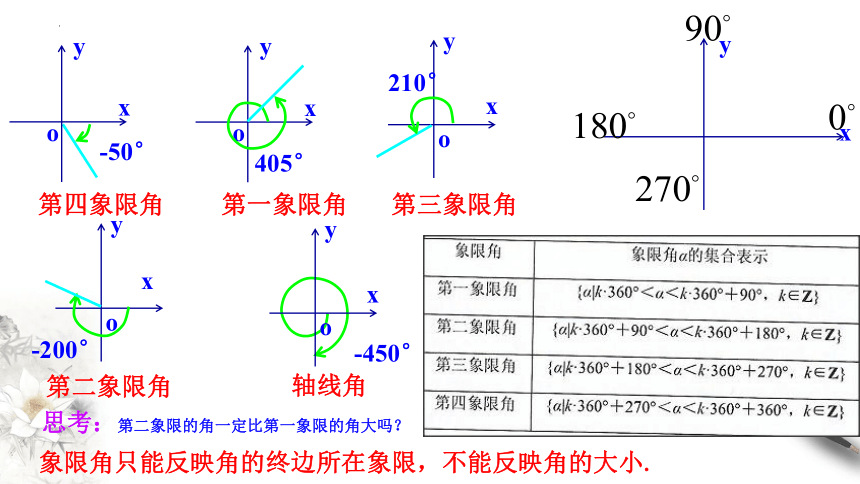
-50°
x
y
o
x
y
o
210°
-450°
x
y
o
405°
x
y
o
-200°
x
y
o
第四象限角
第一象限角
第三象限角
第二象限角
轴线角
x
y
思考:第二象限的角一定比第一象限的角大吗?
象限角只能反映角的终边所在象限,不能反映角的大小.
练习
D
例1 在0°~360°范围内,找出与-950°12′角终边
相同的角,并判定它是第几象限角.
4、轴线角
x
y
例2 写出终边在y轴上的角的集合.
解:在0°~360°范围内,终边在y轴上的角有两
个,即90°,270°角(如图).因此,所有与
90°角终边相同的角构成集合
S1={β|β=90°+k·360°.k∈Z}.
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°.k∈Z}.
于是,终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+180°+2k·180°,k∈Z }
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+(2k+1)180°,k∈Z }
={β|β=90°+n·180°,n∈Z }
例3.写出终边在直线y=x上的角的集合S,并把S中适合不等式-360°≤α<720°的元素β写出来.
【解析】S={β|β=45°+k·180°,k∈Z}.
S中适合不等式-360°≤β<720°的元素有:
-315°,-135°,45°,225°,405°,585°.
4、区间角
例1
变式练习
巩固练习
5.角的终边对称
题型分析 举一反三
题型一 任意角和象限角的概念
解题方法(任意角和象限角的表示)
1.判断角的概念问题的关键与技巧.
(1)关键:正确的理解角的有关概念,如锐角、平角等;
(2)技巧:注意“旋转方向决定角的正负,旋转幅度决定角的绝对值大小.
2.象限角的判定方法.
(1)图示法:在坐标系中画出相应的角,观察终边的位置,确定象限.
(2)利用终边相同的角:第一步,将α写成α=k·360°+β(k∈Z,0°≤β<360°)的形式;
第二步,判断β的终边所在的象限;
第三步,根据β的终边所在的象限,即可确定α的终边所在的象限.
题型二 终边相同的角的表示及应用
答案:(1)(-3)×360°+195°(2)见解析
解析:(1)-885°=-1 080°+195°=(-3)×360°+195°.
(2)与α=-910°终边相同的角的集合为{β|β=k·360°-910°,k∈Z},
∵-720°<β<360°,即-720°<k·360°-910°<360°,k∈Z,
∴k取1,2,3.
当k=1时,β=360°-910°=-550°;
当k=2时,β=2×360°-910°=-190°;
当k=3时,β=3×360°-910°=170°.
解题方法(终边相同的角的表示)
1.在0°到360°范围内找与给定角终边相同的角的方法
(1)一般地,可以将所给的角α化成k·360°+β的形式(其中0°≤β<360°,k∈Z),其中β就是所求的角.
(2)如果所给的角的绝对值不是很大,可以通过如下方法完成:当所给角是负角时,采用连续加360°的方式;当所给角是正角时,采用连续减360°的方式,直到所得结果达到所求为止.
2.运用终边相同的角的注意点
所有与角α终边相同的角,连同角α在内可以用式子k·360°+α,k∈Z表示,在运用时需注意以下四点:
(1)k是整数,这个条件不能漏掉.
(2)α是任意角.
(3)k·360°与α之间用“+”连接,如k·360°-30°应看成k·360°+(-30°),k∈Z.
(4)终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数个,它们相差周角的整数倍.
题型三 任意角终边位置的确定和表示
解题方法(任意角终边位置的确定和表示 )
1.表示区间角的三个步骤:
第一步:先按逆时针的方向找到区域的起始和终止边界;
第二步:按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α第三步:起始、终止边界对应角α,β再加上360°的整数倍,即得区间角集合.
2.nα或所在象限的判断方法:
(1)用不等式表示出角nα或的范围;
(2)用旋转的观点确定角nα或所在象限.
1.如图所示的图形,那么终边落在阴影部分的角的集合如何表示?
解析:在0°~360°范围内,终边落在阴影部分(包括边界)的角为60°≤β<105°与240°≤β<285°,所以所有满足题意的角β为{β|k·360°+60°≤β+285°,k∈Z}={β|2k·180°+60°≤β<2k·180°+105°,k∈Z}
∪{β|(2k+1)·180°+60°≤β<(2k+1)·180°+105°,k∈Z}=
{β|n·180°+60°≤β故角β的取值集合为{β|n·180°+60°≤β
人教2019版必修第一册
第五章 三角函数
5.1.1 任意角
课程目标
1.了解任意角的概念.
2.理解象限角的概念及终边相同的角的含义.
3.掌握判断象限角及表示终边相同的角的方法.
数学学科素养
1.数学抽象:理解任意角的概念,能区分各类角;
2.逻辑推理:求区间角;
3.数学运算:会判断象限角及终边相同的角.
自主预习,回答问题
阅读课本168-170页,思考并完成以下问题
1.角是如何推广的 角的概念推广后,分类的标准是什么?
2.如何判断角所在的象限?
3.终边相同的角一定相等吗?如何表示终边相同的角?
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
射线
旋转
图形
角的构成要素
始边
终边
顶点
A
B
O
方向
逆时针
顺时针
(4)相等角、相反角、两角的加减运算(和角与差角)
相等角:
和角:
把射线OA绕端点O按不同方向旋转相同的量所成的两个角叫做互为相
反角。
相反角:
差角:
原点
x
终边
象限角
坐标轴上
-50°
x
y
o
x
y
o
210°
-450°
x
y
o
405°
x
y
o
-200°
x
y
o
第四象限角
第一象限角
第三象限角
第二象限角
轴线角
x
y
思考:第二象限的角一定比第一象限的角大吗?
象限角只能反映角的终边所在象限,不能反映角的大小.
练习
D
例1 在0°~360°范围内,找出与-950°12′角终边
相同的角,并判定它是第几象限角.
4、轴线角
x
y
例2 写出终边在y轴上的角的集合.
解:在0°~360°范围内,终边在y轴上的角有两
个,即90°,270°角(如图).因此,所有与
90°角终边相同的角构成集合
S1={β|β=90°+k·360°.k∈Z}.
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°.k∈Z}.
于是,终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+180°+2k·180°,k∈Z }
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+(2k+1)180°,k∈Z }
={β|β=90°+n·180°,n∈Z }
例3.写出终边在直线y=x上的角的集合S,并把S中适合不等式-360°≤α<720°的元素β写出来.
【解析】S={β|β=45°+k·180°,k∈Z}.
S中适合不等式-360°≤β<720°的元素有:
-315°,-135°,45°,225°,405°,585°.
4、区间角
例1
变式练习
巩固练习
5.角的终边对称
题型分析 举一反三
题型一 任意角和象限角的概念
解题方法(任意角和象限角的表示)
1.判断角的概念问题的关键与技巧.
(1)关键:正确的理解角的有关概念,如锐角、平角等;
(2)技巧:注意“旋转方向决定角的正负,旋转幅度决定角的绝对值大小.
2.象限角的判定方法.
(1)图示法:在坐标系中画出相应的角,观察终边的位置,确定象限.
(2)利用终边相同的角:第一步,将α写成α=k·360°+β(k∈Z,0°≤β<360°)的形式;
第二步,判断β的终边所在的象限;
第三步,根据β的终边所在的象限,即可确定α的终边所在的象限.
题型二 终边相同的角的表示及应用
答案:(1)(-3)×360°+195°(2)见解析
解析:(1)-885°=-1 080°+195°=(-3)×360°+195°.
(2)与α=-910°终边相同的角的集合为{β|β=k·360°-910°,k∈Z},
∵-720°<β<360°,即-720°<k·360°-910°<360°,k∈Z,
∴k取1,2,3.
当k=1时,β=360°-910°=-550°;
当k=2时,β=2×360°-910°=-190°;
当k=3时,β=3×360°-910°=170°.
解题方法(终边相同的角的表示)
1.在0°到360°范围内找与给定角终边相同的角的方法
(1)一般地,可以将所给的角α化成k·360°+β的形式(其中0°≤β<360°,k∈Z),其中β就是所求的角.
(2)如果所给的角的绝对值不是很大,可以通过如下方法完成:当所给角是负角时,采用连续加360°的方式;当所给角是正角时,采用连续减360°的方式,直到所得结果达到所求为止.
2.运用终边相同的角的注意点
所有与角α终边相同的角,连同角α在内可以用式子k·360°+α,k∈Z表示,在运用时需注意以下四点:
(1)k是整数,这个条件不能漏掉.
(2)α是任意角.
(3)k·360°与α之间用“+”连接,如k·360°-30°应看成k·360°+(-30°),k∈Z.
(4)终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数个,它们相差周角的整数倍.
题型三 任意角终边位置的确定和表示
解题方法(任意角终边位置的确定和表示 )
1.表示区间角的三个步骤:
第一步:先按逆时针的方向找到区域的起始和终止边界;
第二步:按由小到大分别标出起始和终止边界对应的-360°~360°范围内的角α和β,写出最简区间{x|α
2.nα或所在象限的判断方法:
(1)用不等式表示出角nα或的范围;
(2)用旋转的观点确定角nα或所在象限.
1.如图所示的图形,那么终边落在阴影部分的角的集合如何表示?
解析:在0°~360°范围内,终边落在阴影部分(包括边界)的角为60°≤β<105°与240°≤β<285°,所以所有满足题意的角β为{β|k·360°+60°≤β
∪{β|(2k+1)·180°+60°≤β<(2k+1)·180°+105°,k∈Z}=
{β|n·180°+60°≤β
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
